基于小波和自适应模糊神经的旋转设备故障诊断

王志伟,胡 瑜,李银伟

(华东交通大学载运工具与装备省部共建教育部重点实验室,江西南昌330013)

随着现代科学技术的进步和生产系统的不断发展,旋转设备已被广泛应用于工业系统的各个领域。但是,旋转设备在长时间的正常工作中,由于运行中自身的负荷、周围环境等各种因素,不可避免地会产生故障。故障一旦发生就可能破坏整台设备甚至影响整个生产过程,造成巨大经济损失,甚至给人们的生命带来灾难[1]。及时准确地发现设备潜在的或现有的故障是保证设备安全运行的重要措施,具有重要的理论研究价值和工程实践意义。而故障诊断方法在旋转设备中的应用,正是满足了旋转设备在这方面的要求。

现有的故障诊断方法可以分成两大类:传统故障诊断方法和基于人工智能的故障诊断方法。由于传统的故障诊断方法,需要建立精确的数学模型、有效的状态估计或参数估计、适当的统计决策方法等前提条件,使得传统的故障诊断具有相当大的局限性[2]。人工智能方法,如神经网络、模糊逻辑、模糊神经和遗传算法等在故障诊断中的应用,能够处理传统故障诊断方法无法解决的问题,使得故障诊断的人工智能方法在近几年得到广泛的认可和应用,已被认为是故障诊断技术的重要发展方向。

随着现代工业的发展,自动化系统的规模越来越大,其产生故障的可能性和复杂性剧增,仅靠一种理论或一种方法,无论是智能的还是经典的,都很难实现复杂条件下对故障完全、准确、及时地诊断,而多种方法综合运用,既可是经典方法与智能方法的结合,也可是两种或多种智能方法的结合,兼顾了实时性和精确度,因此多种方法的有机融合、综合运用这一趋势将成为必然,也将成为故障诊断技术发展的主流方向。本文将小波分析的特征提取方法和自适应模糊神经网络故障诊断方法相结合,并应用于旋转设备故障诊断系统中,与传统的诊断方法和单独使用一种智能诊断方法相比,取得了更加快速、准确的诊断效果。

1 故障诊断技术路线及基本原理

1.1 故障诊断的技术路线

旋转设备故障诊断主要由5个步骤组成:

(1)转子振动信号的检测与采集;

(2)信号处理与分析;

(3)从处理过后的信号中提取特征量;

(4)依据所获得特征量对旋转设备进行故障诊断;

(5)诊断结果的输出和判断。

图1为电机故障诊断技术路线。

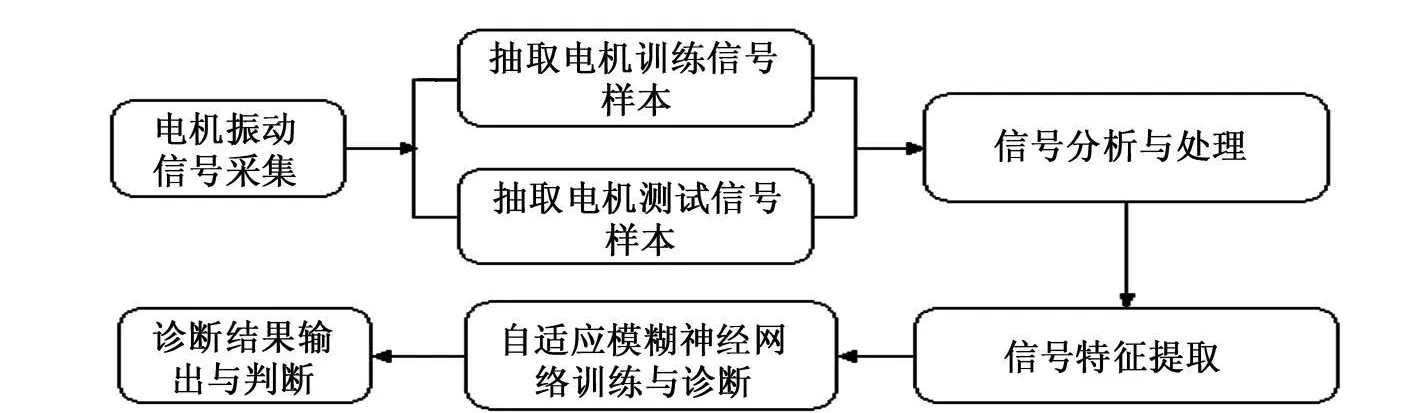
图1 电机故障诊断技术路线图

1.2 小波分析与信号特征提取

小波变换(Wavelet Transform)是一种新的时-频分析方法,具有多分辨串的特点,而且在时-频两域都具有表征信号局部特征的能力[3]。正是由于小波变换具有良好的时-频局域化性质,为信号检测、特征参数提取等方面提供了一条有效的途径。

1.2.1 小波分析原理

则信号f(t)的连续小波变换在L2R中被定义为

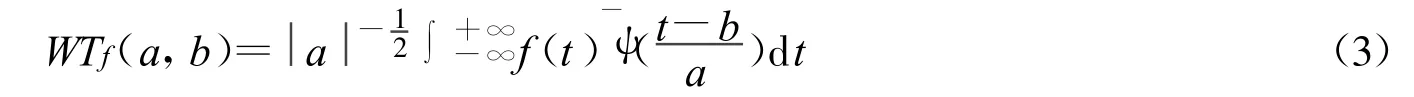
从式(4)可以看出,它是一个双参数带通滤波器,其中参数 a称为伸缩因子,它改变滤波器的频带宽度,从而决定了小波变换中的频率信息。参数b称为平移因子,它决定了变换结果中的时域信息,由此可以看出,小波函数同时具有频域和时域定位特性。WTf(a,b)称为小波变换系数。小波变换的实质就是以基函数的形式将信号f(t)分解为不同频带的子信号。

1.2.2 基于小波包特征量的提取

小波包分析(Wavelet Packet Analysis)能够为信号提供一种更加精细的分析方法,它将频带进行多层次划分,对多分辨分析没有细分的部分进一步分解,并能够根据被分析信号的特征,自适应地选择相应频带,使之与信号频谱相匹配,使低频和高频成分都达到很精细的程度,从而提高时频分辨率,因此小波包具有更广泛的应用价值[4]。

1.2.2.1 小波包Mallat分解算法

式中:hk,gk为小波分解的共轭滤波器系数;j为分解的层数;d为小波包分解频带的小波系数。

如果要观察某个频段上的时域波形,则保留这一频段上的信号,其它频段上的数据置为零,再用小波包重构算法,对信号进行重构。

1.2.2.2 小波包Mallat重构算法

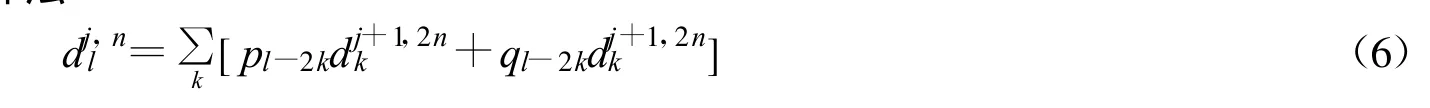
式中:pk,qk为小波重构共轭滤波器系数

1.2.2.3 故障特征提取

当设备出现故障时,会对各频带内信号的能量有较大的影响,因此,以小波包分解重构后各频段“能量”为元素构造旋转设备故障信号的特征向量。可有效提取故障特征,从而为旋转设备的故障智能诊断提供了一种便捷的处理方法。其基本步骤为:(1)对信号小波包分解;(2)消噪、重构小波包系数;(3)计算各频段信号的能量,作为特征值;(4)对特征向量进行归一化处理;(5)构造特征向量。故障特征提取过程中,对信号进行小波包分解的层数视具体信号和对特征参数的要求决定。要适当选择小波包分解的层数,分解层数过少,不能有效提取故障特征;分解层数过多,特征向量的维数大,会影响诊断的速度。

1.3 自适应模糊神经网络故障诊断方法

模糊系统和神经网络有很多互补的特点,可以实现故障诊断系统对不精确或不确定等模糊信息的处理。基于神经网络的自适应模糊推理系统(ANFIS)就是这种结合的产物。利用神经网络的学习机制补偿模糊推理的缺点,两者结合形成的模糊神经网络具有模糊逻辑易于表达人类知识和神经网络分布式信息存储及自学习的优点,为复杂系统的建模和控制提供了有效的工具。图2为模糊神经网络原理图。

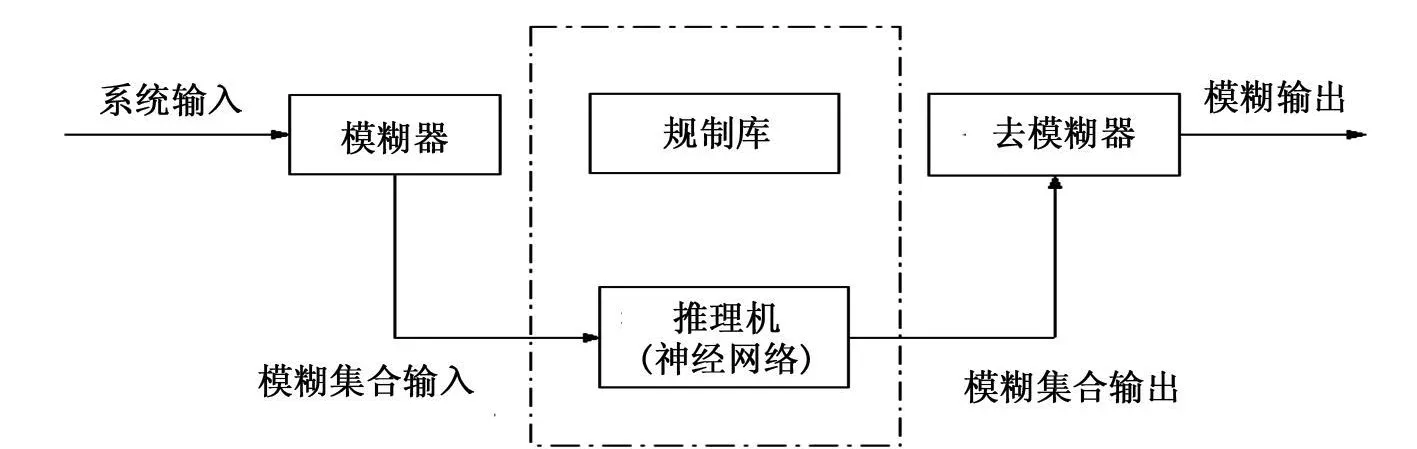
图2 模糊神经网络原理图

为便于阐述,假定采用Takagi-Sugeno[5]型模糊规则的ANFIS系统有两个输入x和y,一个输出f,并含有以下两条规则:

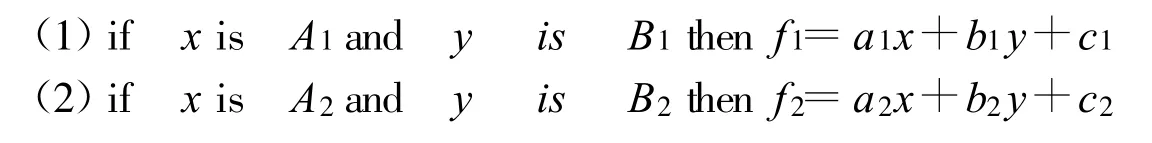
其自适应模糊神经推理系统结构如图3所示。

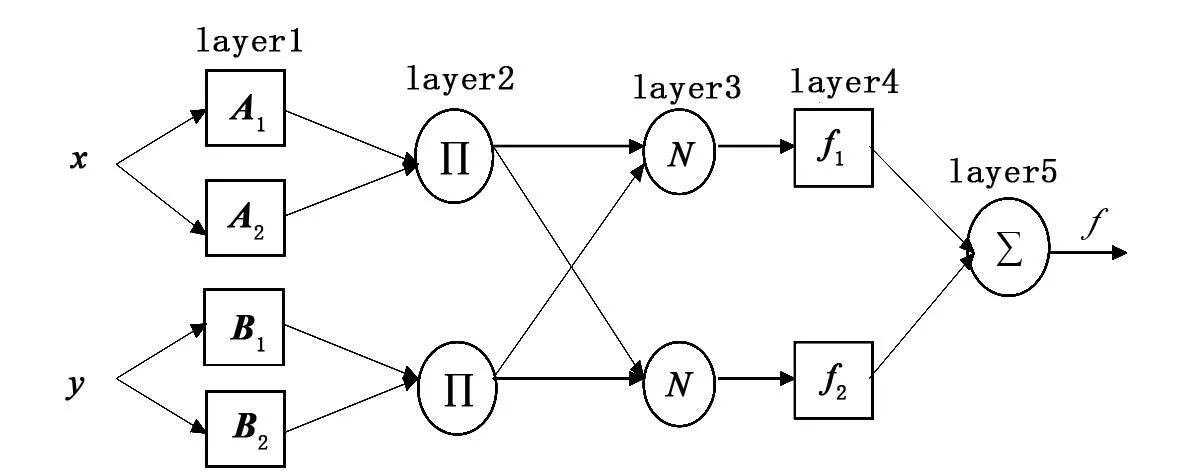
图3 自适应模糊神经结构图

依据模糊系统的推理规则各层的功能分别为

(1)输入变量模糊化,求出 x和y对模糊子集A1和A2的隶属度,输出为

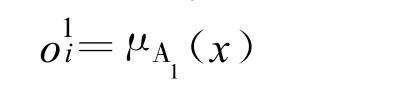
(2)输出为输入信号的乘机,其意义是样本对规则的激活强度

(3)归一化各条规则的激活强度

ANFIS的学习算法:采用HYBRID混合学习法[6]。在混合学习法的前向通道中,各个节点的输出可向前输出至第4层,用最小二乘法辨识结论参数;在反向通道中,误差信号反传,并用梯度法更新前件参数。采用混合学习算法,对于给定的前件参数,可以得到后件参数的全局最优点,这样不仅可以降低梯度下降法中搜索空间的维数,还可以大大提高参数的收敛速度。

(4)去模糊化,各节点计算出相应规则的输出

(5)计算所有规则的输出之和

2 电机故障诊断

2.1 电机故障诊断的思路

由电机故障试验台采集电机转子不平衡、转子不对中和油膜振荡3种故障振动信号,将得到的样本信号分成训练和测试两组信号,接下来分别对两组信号进行小波消噪处理、然后利用小波函数对消噪后的信号进行3层小波包分解与重构,并以第3层各频带信号的能量为元素构造特征向量,提取故障特征,最后通过MATLAB中的ANFIS工具箱[7]对故障进行诊断。本文利用电机故障诊断试验台采集到的振动信号经小波包分解重构后,以0～0.125f,0.125～0.25f,0.25～0.375f,0.375～0.5f,0.5～0.625f,0.625～0.75f,0.75～0.875f,0.875～1f,f为分析上限频率)8个频段的能量为构造的特征向量,并对特征数据进行归一化处理后,作为自适应模糊神经网络的输入。表1和表2分别为训练样本和测试样本信号的特征数据。

表1 训练样本信号特征数据

表2 测试样本信号特征数据

2.2 电机故障诊断仿真实验

利用MATLAB中的自适应模糊神经网络编辑器,对特征数据处理如下:(1)加载数据,分别将训练数据和测试数据加载到系统中;(2)生成模糊推理系统,初始化系统,设置隶属度函数的数目、类型和输出隶属度函数的类型;(3)训练自适应模糊神经推理系统,并选择优化方法、误差精度和训练次数;(4)测试模糊推理系统;(5)查看自适应模糊神经推理系统,并进行评估验证推理系统。

本文中ANFIS相关参数设置为:输入变量的隶属度函数统一取Gauss函数,隶属度函数的个数取2,输出隶属度函数为线性函数;训练的优化方法为混合算法,目标误差为0,训练步数40。数据输出标准模型为:转子不平衡输出为1,转子不对中输出为2,油膜振荡输出为3。图4为ANFIS的训练误差曲线,表3为ANFIS测试样本诊断结果。

同时文中还用BP神经网络对电机的故障进行了诊断,BP神经网络相关参数设置为:输入神经元数为8,输出神经元数为2,分别由两位不同的二进制数表示三种故障类型,综合考虑网络性能选择隐含层神经元数为9,隐含层神经元的传递函数采用tansig,输出层神经元的传递函数采用purelin,目标误差为0,训练步数500。数据标准输出模型为:转子不平衡输出为(0,1),转子不对中输出为(1,0),油膜振荡输出为(1,1)。图5为BP神经网络训练误差曲线,表4为BP神经网络测试样本诊断结果。

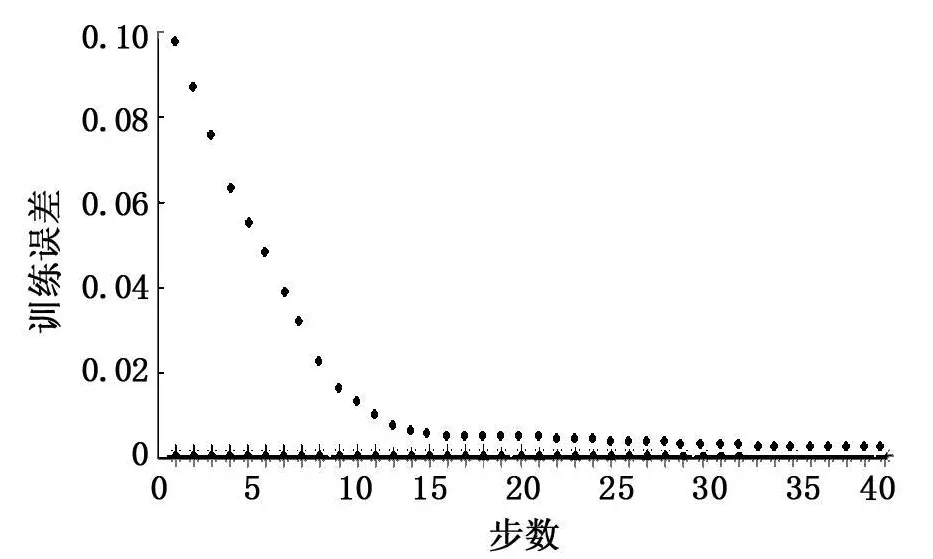
图4 ANFIS的训练误差曲线

图5 BP神经网络训练误差曲线

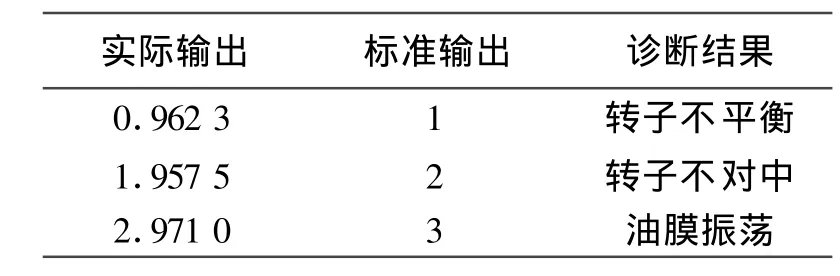
表3 ANFIS测试样本诊断结果

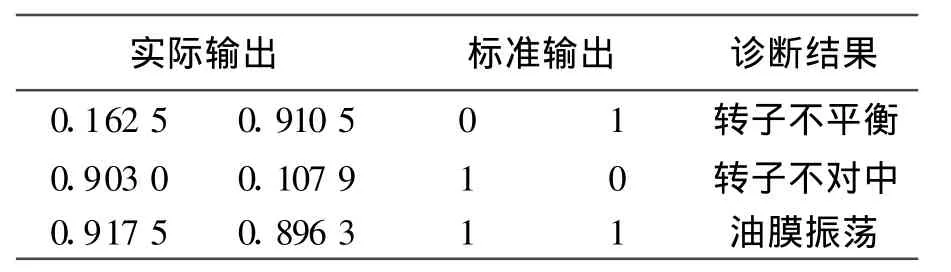
表4 BP神经网络测试样本诊断结果

2.3 仿真结果分析

从表3和表4中可以看出,ANFIS诊断方法和BP神经网络诊断方法都能够准确的识别出电机的3种故障类型。但对比表中的数据结果,ANF1S测试样本诊断结果的平均误差为3.51%,而BP神经网络测试样本诊断结果的平均误差为10.64%,因此相比较而言,ANF1S方法诊断结果的精度要高于BP神经网络;此外,从图4和图5还可以看出,ANF1S误差曲线收敛速度要快于BP神经网络训练的收敛速度,仅用20步左右就已经趋于收敛,而BP神经网络在140步左右时才趋于收敛。

所以综上所述,结合小波分析的自适应模糊神经故障诊断方法,对旋转设备进行故障诊断,相比于单独使用神经网络诊断方法,无论在诊断速度,还是在诊断精度上,都得到了提高。

3 应用实例

本文的实际应用背景是本校实习工厂的一台电机,由于该电机在大负荷及较复杂的周围环境中长时间工作,因此经常出现一些故障,一般情况下都是通过人为检查发生了何种故障,但这种方式既浪费时间,而且不容易查出故障之所在。鉴于这个问题,本文利用以上建立的基于小波分析的故障特征提取方法和自适应模糊神经的故障诊断方法,对该电机进行故障诊断。

该电机型号为Y132S1-2,额定功率5.5 kW,工作电压380 V,工作电流11.1 A,转速2 900 r/min,频率50 Hz,功率因数0.88,采样频率为8 000 Hz,传感器选为加速度传感器。该电机经常出现的故障有转子不平衡、转子不对中、油膜振荡、转子碰磨、转子断条5种故障。首先利用加速度传感器采集电机在五种故障状态下的振动信号,经小波消噪、分解和重构处理后,以0～500 Hz,500～1 000Hz,1 000～1500 Hz,1 500～2 000Hz,2 000～2500Hz,2 500～3 000 Hz,3 000～3 500 Hz,3 500～4 000Hz各分析频段的能量构造特征向量,经归一化后作为自适应模糊神经网络的输入,建立该电机故障诊断的算法模型,在模型建立成功后,就可以在电机出现故障时,利用该模型对电机进行故障诊断。经过一段时间的观察测试,该模型可以准确的、快速的识别电机常见的故障。因此,本文建立的结合小波分析的自适应模糊神经故障诊断方法,应用于实际工程中可行的、有效地。

4 结束语

智能故障诊断方法比传统的故障诊断方法具有更大的优越性,在旋转设备行业和其他工业领域都有广泛的应用。模糊系统具有处理自然语言的能力,表达形式直观易懂,但隶属度函数的确定很大程度上依赖于专家的经验,主观性比较大。神经网络具有自组织、自学习的能力,但内部结构和输出形式不易人们理解。本文将小波分析故障特征提取方法和自适应模糊神经网络结合起来对旋转设备进行故障诊断,充分利用了神经网络和模糊系统的各自优点,实现了优势互补,在应用中得到了很好的故障诊断效果。

[1]罗邦.旋转机械故障诊断技术的研究现状及发展趋势[J].机电产品开发与创新,2008,21(3):85-89.

[2]沈艳霞,纪志成,姜建国.电机故障诊断的人工智能方法综述[J].微特电机,2004(2):39-42.

[3]张定会.基于小波分析的故障诊断.上海理工大学学报[J].2000,22(2):137-140.

[4]张超杰.小波分析在旋转机械故障诊断中的应用[D].大连理工大学,2006.12:29-30.

[5]孙海荣.模糊神经网络的研究与应用[D].华北电力大学,2006.

[6]汤永川,黄天民.一种获取与优化模糊规则基的混合学习算法[J].西南交通大学学报,2000,(1):102-105.

[7]李国勇.神经模糊控制理论及应用[M].电子工业出版社,2009:303-306.