基于FPGA的语音识别前端算法研究实现
2010-07-02刘文姝季爱明王子欧
刘文姝,季爱明,王子欧
(苏州大学,江苏 苏州215021)
近年来,语音识别在通信与电子系统、自动控制等领域中有着广泛的应用。其中一个重要的发展方向是硬件实现语音识别算法的研究。这个方向主要是小型化、便携式语音产品的应用,在这类设备上,通常是小词汇量的孤立词识别,例如:手机﹑PDA以及车载应用等装置上。国外在硬件实现方面的研究较早,而国内起步较晚,因此对基于FPGA的语音识别前端算法研究具有重要的意义[1]。
近两年国际上提出了分布式语音识别DSR(Distributed Speech Recognition)。移动终端只需进行语音采集、特征提取,有关信息则通过无线数据信道送往网络中的远程服务器,由服务器中的识别单元完成语音识别功能[2]。就目前的研究情况来看,通常用相关的方法实现LPCC系数的提取。而在LPC系数提取部分的除法器,采用的结构不尽相同,有采用搜索算法[3],也有采用减并移位法[4];在LPCC系数提取时,可以直接计算,也可以经过一定的变换[5]。为了将面积和性能得到最好的折中,并且考虑实际的应用场合,在以上两个除法器的设计上,进行一定的研究,提出了适合的方案。
1 系统算法实现
本系统是对于语音识别的前端算法研究,要解决的问题是语音采集、特征提取,而语音的识别,则是由远端服务器来完成。一般的特征参数提取流程图包括预加重、加窗、自相关、求 LPC系数和求其倒谱(LPCC)系数。下面将按照各个模块分别研究。
1.1 自相关
对语音信号进行分帧,使得每一帧有N=256个采样,帧移为64。对每一帧信号进行预加重和加窗。
预加重采用:


窗函数采用汉明(Hamming)窗,汉明窗函数要先计算好放于ROM中,直接与语音信号相乘得到加窗的语音信号。对每一帧经过预处理的语音信号进行自相关分析。采用公式:
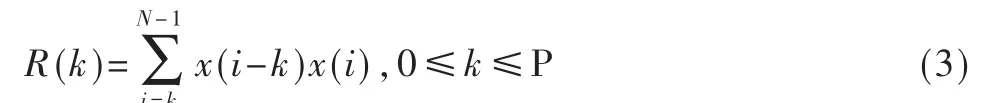
式中P是LPC的阶数,取P=10。所采用结构如图1。
在计算自相关系数的部分,如果在累加部分采用移位寄存器来计算保存11个LPC系数,会产生不必要的移位功耗[6]。考虑到FPGA丰富的存储器资源,采用RAM进行累加部分的计算,从而使功耗得到降低,如图1所示。寄存器的输出形成了连接到加法器的数据通路,而加法器的输出存储在指定位置的寄存器中,主状态机提供操作地址,并控制读﹑写次序以避免在同一位置同时进行读写操作。采用此结构,可以避免不必要的移位功耗,而性能上与采用移位寄存器无差别,故优于后者。
1.2 LPC系数
采用自相关法来计算LPC系数。解LPC系数的矩阵方程为:
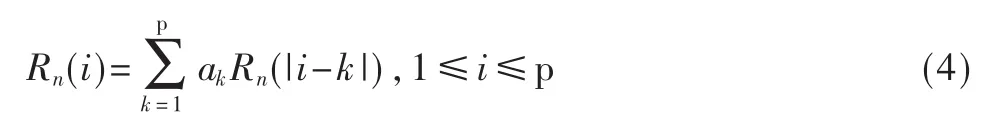
式中P是LPC的阶数,取10阶。采用Levinson-Durbin[7]方法来解。在该方法的计算中,可以看到求偏相关系数(Parcor)k时,由于存在式(5)中的关系:

故在该模块中,除法器的设计是一个关键性的问题。
常用的除法器设计算法多采用多次迭代的方法,如恢复余数方法和减并移位方法等。这类方法虽然比软件除法要快很多,但多次迭代延时还是很大。而且迭代次数与数据相关,使除法器延时不定。在语音处理这类数据量大﹑对运算要求高的领域,迫切需要一种能够采用流水线方法实现的高性能除法器。有的方案文献当中提到采用剪除搜索方法[8]。但是,采用这种方法仍需要相对较长的时间,并且仍不能消除延时不稳定的问题。所以采用一种新的除法器架构——流水线查找表法[9]。
流水线除法器可采用被除数和除数的倒数相乘实现。除数的倒数利用泰勒级数展开算法展开,取前几项通过查表法得到倒数结果。这就是本除法器设计的基本思想。以泰勒级数为基础,根据公式误差对除法面积的影响,采用一个2级流水的单精度除法器。该除法器利用查表法和2个乘法器实现,在面积上要大于搜索算法,但是在时钟周期上,只是2个乘法器或者是一个乘法器和一个LUT的延时,显然比搜索算法的N(数据的位数)个时钟周期短得多。该除法器有2点好处:一是2个乘法和查表可以并行执行,除法器延时较短;二是乘法数据位数较少,乘法器面积较小,而由其决定的LUT面积也不大[8]。两种除法器算法性能比较如表1。

表1 两种除法器算法性能比较表格
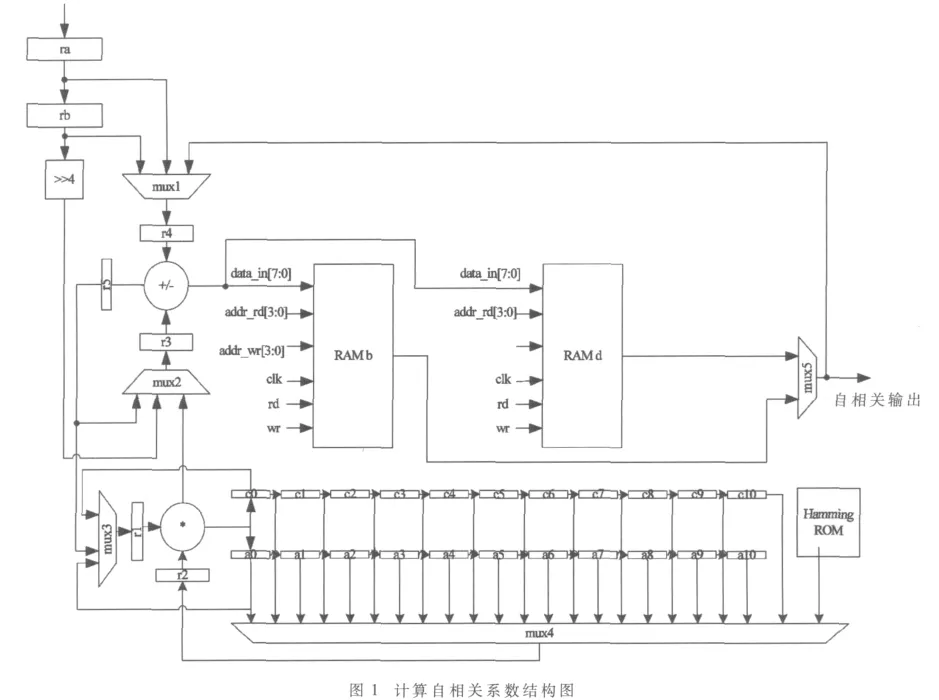
图1 计算自相关系数结构图
其中为了达到资源共享,除法器当中的乘法器和计算结构的乘法器复用,如图2所示。
1.3 LPCC系数
语音信号处理当中,由LPC系数计算LPCC系数的公式如下[7]:

P是LPC的阶数,Q是LPCC的阶数。
按照上面的分析,如果依计算公式计算,缺点是资源占用过多,需要时钟周期过长。所以采用节省资源的方法计算中间系数,对公式进行一定的变形,算法进行一定的改进,资源得到充分利用,并且能够缩短时钟周期,节省乘法器资源57%[5]。计算LPCC系数结构图,如图3所示。
实现节省资源的方法:

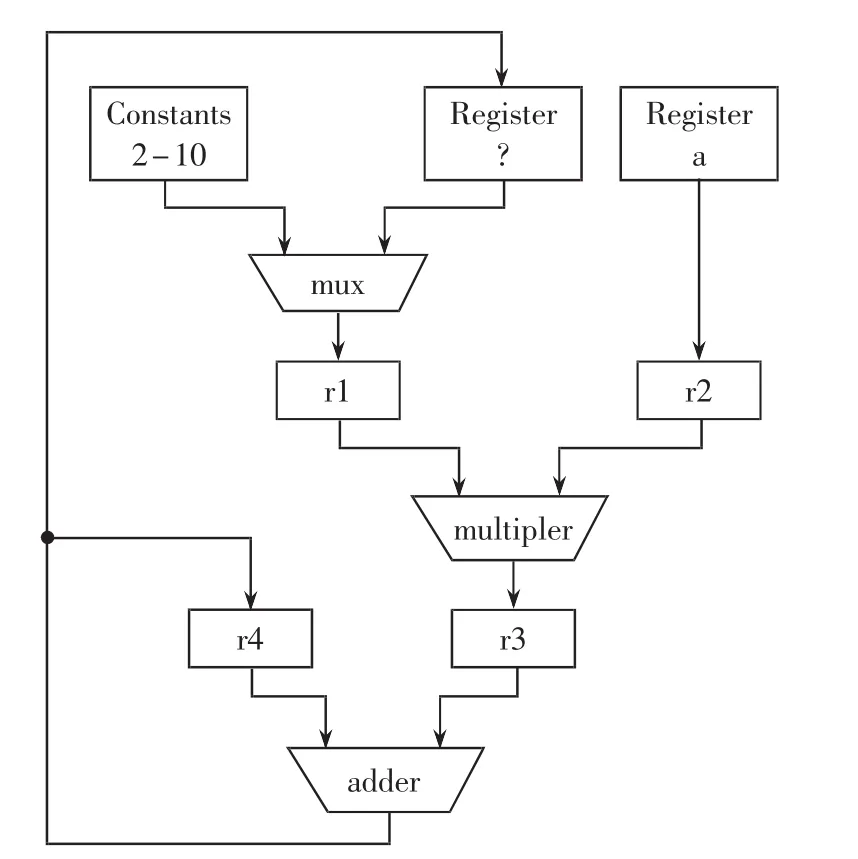
图3 计算LPCC系数结构图
其中P是LPC的阶数,Q是LPCC的阶数,取P=Q=10。
然而,在这个结构当中,可以看到最终的计算结果是ξ,而并不是真正的LPCC系数。为此仍需要一个除法器。这里的除法运算所涉及到的除数仅为一组有限的常数,采用一个通用的除法器就显得没有必要了。为此使用文献[10]中提到的专用常数除法器,它的主要运算部分由规则的处理单元阵列所构成,大大节省面积,易于实现并易于扩展。
2 仿真验证
为了验证算法的可行性,本文用VerilogHDL语言对整个语音参数的提取进行建模。依照图2进行了LPC系数的提取。为了观察方便,本文采用32 bit常数作为自相关系数输入,输出LPC系数是16 bit输出。从仿真结果可以看到,在99 ns时刻,icorrlt_over信号有效,开始计算LPC系数;在8 155 ns时刻,计算得到第一个LPCC系数,在8 395 ns时刻,计算完毕得到一组LPC系数(10阶)。仿真波形表明,此电路的输出结果在整数位宽相同的情况下,与Matlab的仿真结果一致。
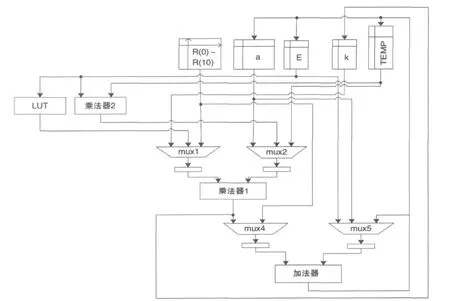
图2 计算LPC系数结构图
依照图3进行了LPCC系数的提取。为了观察方便,本文采用16 bit常数作为LPC系数输入,输出LPCC系数是16 bit输出。从仿真结果可以看到,在99 ns时刻,ilpc_over信号有效,开始计算 LPCC系数;在 8 155 ns时刻,计算得到第一个LPCC系数,在8375 ns时刻,计算完毕得到一组LPC系数(10阶)。仿真波形表明,此电路的输出结果在整数位宽相同的情况下,与Matlab的仿真结果一致。
本文提出了一种前端处理系统的新结构。通过当中除法器的改进设计,在LPC计算部分采用了LUT查找表除法器。经过仿真,并与搜索算法比较,结果表明能够在较短的时钟周期内计算出LPC系数,较之前的方法,节省了大量的运算时间。在LPCC计算部分采用了常数除法器,经过仿真,结果表明与通用的除法器相比,节省了面积,性能良好。
[1]李韬,贺前华,王前.语音识别算法的VLSI实现研究 [J].微电子学,2004(6).
[2]梁钊.分布式语音识别系统及其相关技术[J].计算机工程与应用,2002(12).
[3]WU Gin Der,ZHU Zhen Wei.Chip design of LPC-cepstrum for speech recognition[A].6th IEEE/ACIS International Conference on Computer and Information Science(ICIS 2007).
[4]MICHAEL D C.VerilogHDL高级数字设计[M].北京:电子工业出版社,2005:538-550.
[5]FELICI M,BORGATTI M,FERRARI A,et al.A Low-Power VLSI feature extractor for speech recognition[J].IEEE,1998.
[6]WANG Jhing Fa,WANG Jia Ching,CHEN Han Chiang,et al.Chip design of portable speech memopad suitable for persons with visual disabilities[J].IEEE transactions on speech and audio processing,2002,10(8).
[7]赵力.语音信号处理[M].机械工业出版社,2007:59-62.
[8]WANG Jhing Fa,LIU Liang Ying,CHENG Chung Heng,et al.An ASIC design for linear predictive coding of speech signas[J].0-8186-2845-6/92,1992,IEEE.
[9]朱建银,沈海斌.高性能单精度除法器的实现[J].微电子学与计算机,2007,24(5).
[10]丁保延,章倩苓.常数除法器的设计及其BIST实现[J].半导体学报,2000,21(5).
