化学计量点电位的多元模拟求证

申贵隽孟梁刘玉凤

(1大连大学环境与化学工程学院 辽宁大连116622;2大连大学医学院 辽宁大连116622)

化学计量点电位的多元模拟求证

申贵隽1孟梁1刘玉凤2

(1大连大学环境与化学工程学院 辽宁大连116622;2大连大学医学院 辽宁大连116622)

对分析化学中化学计量点电位的计算公式进行了多元模拟推导。通过对化学计量点电位的求证，得出基础学科间的相互联系和氧化还原反应过程中电极电位变化的基本规律。

滴定分析是通过测定滴定反应达到化学计量点时所用标准物质的量，由计量关系求得被测物质含量的方法。在滴定分析中，确定计量点是最重要的。化学计量点电位的计算是氧化还原滴定技术中的重要组成部分，也是预测氧化还原反应方向和程度的重要依据。然而在氧化还原滴定中，由于氧化还原反应的计量关系比较复杂，不同类型的氧化还原计量点电位的计算容易出现错误。在现行的分析化学教材中，一般是通过能斯特方程来求出化学计量点电位的计算公式［1－2］。从推导过程可以看到在氧化还原过程中达到平衡状态时的各反应物和生成物浓度、电极电位的变化结果，但不能形象地揭示在氧化还原过程中电极电位的变化原因、趋势和速度等潜在因素。为使学生能通过求证过程充分地认识氧化还原反应的基本规律，降低学生对公式求证的理解难度并便于记忆，我们从学科间的相互联系入手，建立了“化学”、“物理”、“数学”3种模拟求证方法。到目前为止，这种多元模拟求证计量点电极电位的方法还未见文献报道。

1 化学计量点电位的多元模拟求证

1.1 化学模拟法

化学模拟法即常规推导法，是教科书中通用的一种求证途径。该方法求证的依据是两个半反应达到化学计量点且处于平衡状态时，两电对的电极电位相等［1－2］。

求证过程如下。

两半反应均为对称反应的氧化还原反应通式为:

半反应:

当氧化还原反应达到平衡时，两电对的电极电位与氧化还原型浓度的关系符合能斯特方程，即:

当反应达到化学计量点且处于平衡状态时，两电对的电极电位相等，即:

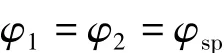
n1×式(1)+n2×式(2)，得:

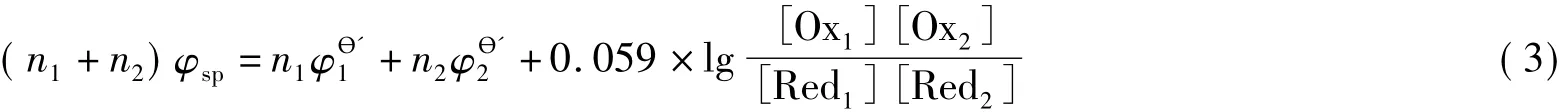
当滴定反应达到化学计量点时，溶液中的各组分浓度有如下关系:

1.2 数学模拟法

数学模拟法利用化学反应中氧化剂、还原剂转移的电子数目相对于电子转移总数的比例求得计量点时的电极电位。在氧化还原反应中，氧化剂、还原剂电对的电极电位之差导致物质间电子的转移，其变化结果是二者电极电位相等。求证化学计量点电极电位就是求解电极电位相等时的变化终点。为此，可以将化学计量点电极电位的求证模拟成初等数学中的平均值求解问题。

如果氧化、还原过程的电子转移个数相等，可以认为参加平均化的数据条件等同，将这些数据直接加和再除以2即可求得平均值——化学计量点电极电位，这种情况可以模拟成等比例分配问题。

对于氧化、还原过程的电子转移个数不相等的氧化还原反应而言，化学反应计量点的电极电位是两电对共同作用达到平衡时的结果，所以应该将氧化还原反应计量点电极电位计算的问题模拟成氧化剂、还原剂初始电极电位的按比例分配问题，即按一定比例系数求解非平均状态下的平均值。由于某电对初始电极电位达到计量点时的电极电位改变幅度(即按比例分配的结果——平均值)的大小与自身的电子转移数直接相关，所以数据平均值的求解途径应该是将乘以一定比例系数的数据逐一加和，这个按比例分配的比例系数应该是在反应过程中该电对转移的电子个数与两个电对的电子转移总数之比。

用比例分配法求证化学计量点时的电极电位为:

1.3 物理模拟法

在教学中，先通过类比将化学语言转变为物理语言。即将电位差模拟成物体的位移差，将与电子转移数相关的氧化还原反应速度模拟成物体对应于原点坐标的位移速度。当两个电极电位不同的物质相邻并发生电子转移时，高电位电对的电极电位逐渐降低、低电位电对的电极电位逐渐升高，最终二者电位相等，反应处于化学平衡状态。氧化剂和还原剂之间电位差的存在是这个氧化还原反应发生的前提。在此把两个状态的电极电位数值φsp与φθ'1、φθ'2分别模拟成不同的平面一维坐标，把氧化剂和还原剂在反应前后电极电位的改变数值分别模拟成两个相向移动物体的一维距离。另外，决定氧化剂、还原剂相对反应速度的主要因素是它们的电子转移数目。在此同样把氧化还原反应过程中的电子转移数目模拟成物体一维相向位移的速度(图1)，这样就可以将求化学计量点电极电位的问题转变为求解两个相向运动物体相遇点一维坐标的问题。利用学生在中学物理学过的运动学中求解相向相遇问题的方法，可以很容易地求出化学计量点电极电位。

图1 氧化还原反应中电极电位改变的一维相向位移模拟示意图

由图1可得:

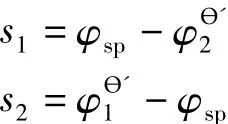
此外，可将n1模拟成v1，n2模拟成v2，根据相遇点时时间相等，有:

因此得:

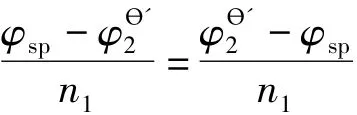
2 讨论

随着学生知识的不断积累，帮助他们巩固与应用所学的知识就显得越来越重要。一题多解、学科交叉、知识综合等教学手段都有利于培养学生对于知识的运用能力。

为了使学生能轻松地理解、掌握所学知识，可以利用已知的、浅显的参照对象做模拟和类比。即应用学生以前所学的知识来由浅入深地推证和解题，这就需要找准新旧知识结合点。教学中所模拟和类比的内容应该是学生熟悉或熟练的知识内容，而且要贴近生活常识，只有这样才有利于学生的理解和记忆。模拟、类比法的作用应该是使复杂问题简单化，如果达不到这一目的就有可能使问题变得更加模糊。只有正确地使用模拟类比法，才能使所求证、求解的复杂问题简单化，抽象问题具体化。如本文所描述的教学事例那样，用这种理论教学模式，可以获得非常简单、清晰、明了的求证。

如何教授学生探索、学习，如何示范把基础理论知识应用于科学和社会发展，是教育工作者面临的重要课题。一个好的教师应善于帮助学生降低教材阅读难度，善于引导学生总结、分类、归纳所学知识，进而优化记忆效率;除此之外，还应该在教学中向学生传授科学解决问题的方法，以培养学生分析问题、解决问题的能力和基本的研究素养。

［1］ 李发美.分析化学.第5版.北京:人民卫生出版社，2006

［2］ 武汉大学.分析化学.第4版.北京:高等教育出版社，2000