液体的表面张力与内压力
2010-07-02黑恩成刘国杰
黑恩成 刘国杰
(华东理工大学化学系 上海200237)
自学之友
液体的表面张力与内压力
黑恩成 刘国杰
(华东理工大学化学系 上海200237)
建立了液体表面张力与内压力间的定量关系,并据此得到了液体表面层的厚度或分子间的有效作用距离。
在涉及液体的表面张力是怎样产生的问题时,有些专著和物理化学教科书是将表面张力与液体的内压力相联系[1-2],阐明两者的区别以及它们之间的密切关系。这对理解液体表面张力的来源有重要的意义。本文试图进一步从定量角度来阐明这个问题,并从中引出有价值的信息。
1 表面张力与内压力
若有一纯物质液体与其气相共存,不难理解,液体体相中的分子与表面层分子的受力状况是不相同的。体相中的分子受周围分子的作用力是各向均等的,分子犹如在一个均匀的力场中自由地运动;而表面层中的分子受周围分子的作用则是各向不均等的。由于通常气相的密度远低于液相,致使表面层分子的受力是不对称的,它们会受到垂直于表面且方向指向液体体相的合力的作用,这个合力来自液体分子间的作用,单位面积的这个作用力便称为内压力。
表面层中的分子正是由于受到内压力的作用,使它们产生一种避离表面的倾向。于是,在可能的情况下,液体将尽可能地缩小其表面积。这种倾向犹如表面有一层绷紧的薄膜,使其受到一种收缩张力的作用,表面上单位长度的收缩张力便称为表面张力或界面张力。
由此可见,表面张力与内压力是两个不同概念的力,前者作用于表面,力的作用方向与表面相切,其作用是使表面尽可能缩小;而后者则源于分子间作用力的合力,其作用方向垂直于表面且指向液体的体相。这两种力密切相关,实为因果关系。有些专著[2-3]用图1所示的力学类比来形象地表示两者间的关系犹如用滑轮举起重物,举重所做的功即为水平方向拉力所做的功,意即扩大液体表面积所增大的表面自由能等于液体从体相反抗内压力移至表面需做之功。本文试图更进一步在两者之间建立定量关系。
2 两种力间的定量关系
设想有一柱状液体,将它拉开分成两半(图2)。若液体的横截面积为A,则不难得到拉开时需做之功为:

式中σ为液体的表面张力。等式右边乘2是因为拉开后形成了两个新的气/液表面。
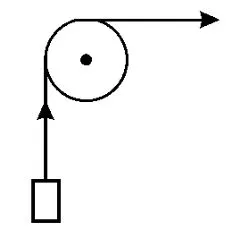
图1 表面张力的力学类比

图2 液体表面张力与内压力间关系的示意图
式(1)意味着拉开液体所做之功被完全用来增加液体的表面自由能,此功亦称内聚功,因为它是将原本内聚在一起的液体拉开分成两半需做的可逆功。显然,这个功是因反抗液体的内聚力亦即分子间的作用力所致。假定分子间的作用合力为F,分子间的有效作用距离为l,则内聚功也可表示为:

因此,由式(1)和式(2)可得:

按照热力学定义,柱状液体的内压力可表示为:


式中pi=(∂U/∂V)T是内压力的热力学定义,式(5)便是本文所得结果。由此可见,表面张力与内压力的关系是很简单的,它不仅说明了纵向作用的内压力与表面上横向作用的表面张力成正比,而且还能说明图1所示的力学类比。图3是该说明的示意图。

图3 力学类比说明示意
图3只表示了气/液表面上一个分子的有效作用范围,它是一个半径为l的圆球。图中piV是体积为V的液体从体相反抗内压力移至表面时需做的可逆功;Fl是将液体拉开而分成两半需做的可逆功,即上面所述的内聚功WC。不难证明,这两个可逆功是等价的,因为如式(4)所示,pi=F/A,而V=Al,其中V是体相中高度为l的液柱体积,A是液柱的横截面积,所以有:

将式(6)代入式(3),可得:

式(7)实际上就是式(5)。这就是说,将体积为V的液体从体相反抗内压力移至表面需做的可逆功与将液体分成两半需做的可逆功等价,都等于表面自由能2σA。
3 液体表面层厚度
所谓表面层厚度,是指液体中分子受力不对称区的厚度。不难明白,这个厚度正好等于液体分子间的有效作用距离l。因为任何与液面的距离小于l的液体分子都有可能与气相分子发生作用,从而使它失去作用力的对称性。现若用δ表示液体表面层的厚度,则因δ=l,式(5)也可表示为:

式(8)提供了一个估算难以测定的液体表面层厚度的简便方法,因为液体的表面张力和内压力都可用实验精确地测定。
表1是用此法算得的结果。表中列出了293.15K时若干非极性或弱极性液体的表面张力和内压力实验值,它们分别取自文献[4]和[5],由式(8)算得的液体表面层厚度δ则列在表1的最后一列。

表1 293.15K时若干液体的表面张力、内压力和表面层厚度
由表1可见,这些液体的表面层厚度相差不大,约为1.5×10-8cm。这是由于这些液体的分子间作用力主要是van derWaals引力,这种力与分子间距的7次方成反比,故分子间的有效作用距离是很短的。这决定了液体表面层的厚度很小,在离开液面大约1个到几个分子直径距离后,分子的受力便各向均等而变为对称了。
4 讨论
应该指出,式(8)仅适用于非极性或弱极性液体。这是因为上述推导认为,液体的表面自由能是由反抗液体分子间的内聚力做功所致,如果将液体分成两半,与环境没有热量交换,则液体的表面自由能完全是由内聚能转变而来,即:

式中-U为液体的内聚能。由于非极性或弱极性液体分子间的作用力主要是van derWaals引力,其内压力可由a/V2表示,故有:
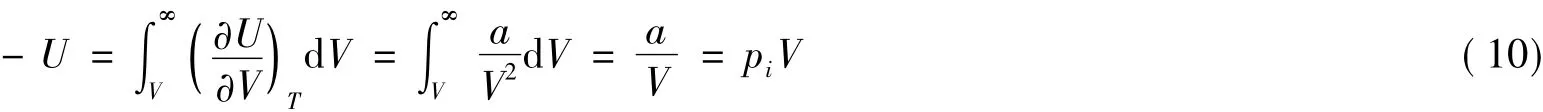
将式(10)代入式(9)即得式(7),其中V=Al。这就是说,将图2所示柱状液体拉开至分子间的有效作用距离l,就相当于将体积为A×l的柱状液体的内聚能转变成了液体的表面自由能,而这种液体则是非极性或弱极性的。
此外,式(8)计算是在气相密度远低于液相密度,以致前者相比于后者可以忽略的情况下得到的,这就是说,表1计算结果仅适用于气液两相远离临界状态的情况。
[1] 胡英,吕瑞东,刘国杰,等.物理化学(上册).第3版.北京:高等教育出版社,1988
[2] 章燕豪.吸附作用.上海:上海科学技术文献出版社,1989
[3] Adamson AW.表面的物理化学(上册).第3版.顾惕人译.北京:科学出版社,1986
[4] Jasper J J.JPhys Chem Ref Data,1972,1:841
[5] Allen G,Gee G,Wilson G J.Polymer,1960,1:456
