用数理统计知识探讨分析化学中的数据处理问题

罗群兴

(西安石油大学化学化工学院2006级 陕西西安710065)

用数理统计知识探讨分析化学中的数据处理问题

罗群兴

(西安石油大学化学化工学院2006级 陕西西安710065)

在分析化学中，误差及分析数据处理是分析化学中的基础知识，而在许多教材中这方面知识给得比较直接、比较简单。本文从数理统计的角度出发详细地解释一些基本概念和具体地推导一些公式，并以数理统计方法解决分析化学中的一些常见问题作为对比。

1 基本概念的解释

1.1 估计值的引入［1］

许多实验，可能存在未知参数θ。我们可以根据一些已知信息去估计这个参数θ，其估计值为^θ。即^θ为θ的估计值。

1.2 系统误差的解释

分析化学中的系统误差是由于在分析过程中某些比较固定的原因造成的，对分析结果的影响比较固定。

而在数理统计中对参数进行估计时，可能会出现不同的估计值，而要确定一个估计值的好坏就必须有多次抽样结果来衡量。或许在一次的抽样中得到的估计值不一定恰好等于待估参数的真值，但是由大量的抽样所得到估计值的平均值应与待估参数真值相同，即无系统偏差。所以可以定义E(^θ)－θ称为以^θ作为θ的估计值的系统误差。其中E是指对抽样结果的值求平均值。

1.3 随机误差的分布服从正态分布的解释

随机误差又称偶然误差，它是由于一些偶然的因素引起的无法控制的误差。如环境的温度、气压等微小波动、仪器性能的微小变化等。

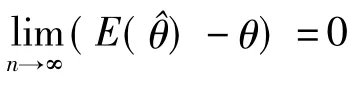
图1 正态分布曲线

2 t分布的引入与推导

2.1 χ2分布的引入［1］

设X1，X2，……，Xn是来自总体N～(0，1)的一个样本，则称χ2=++……+服从自由度为n的χ2分布。

2.2 t分布的推导

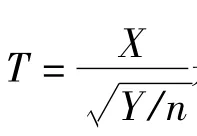
设X1，X2，……，Xn为来自正态总体N～(μ，σ2)的样本，¯X、S2分别为样本均值和样本方差，则有如下性质［2］:

3 置信度和置信区间

3.1 从数理统计的角度引入置信区间和置信度

我们知道在对某一未知参数估计时，其估计值不可能与真值完全相同，而只能落在真值θ的附近，即θ被包含在(^θ－δ，^θ+δ)内，而由于抽样的随机性又决定了θ被该区间包含具有一定概率P(^θ－δ＜μ＜^θ+δ)=1－α。其中(^θ－δ，^θ+δ)为置信区间，1－α为置信度，分别描述的是参数θ的估计值^θ的精确程度和可信程度。

3.2 用数理统计的方法求置信区间并与分析化学课本中方法对比

3.2.1 数理统计方法的推导

设总体X～N(μ，σ2)，σ2已知，μ为未知，若X1，X2，……，Xn是来自X的样本，令:

而N(0，1)分布是不依赖任何未知参数的。按标准正态分布的α分位点(图2)的定义有:

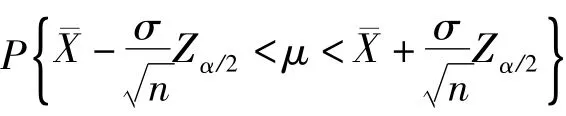
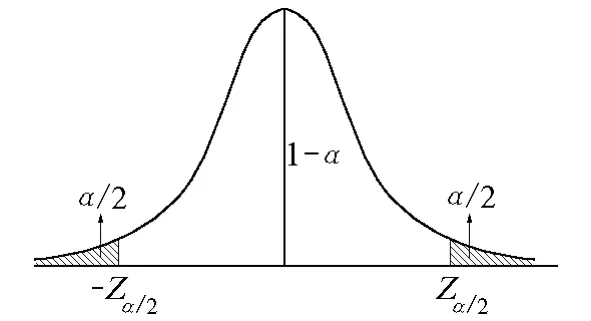
图2 标准正态分布的α分位点

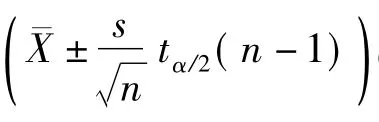
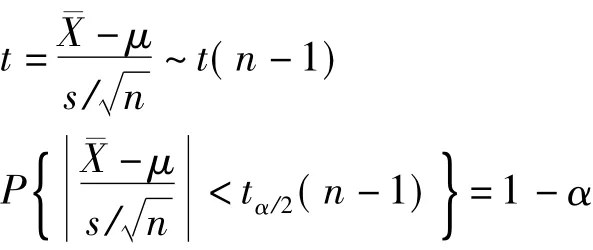
3.2.2 通过分析化学课本［2］中的例题来验证

例:测定SiO2的质量分数，得到下列数据(%):28.62，28.59，28.51，28.48，28.52，28.63。求平均值、标准偏差及置信度为90%时平均值的置信区间。

图3 t分布的α分位点

当置信度为90%时，即1－α=90%，所以α=0.1，α/2=0.05，自由度n－1=5，查t分布表可得tα/2(5)=2.0150。由3.2.1中的结论可得:

4 用数理统计的方法检验分析结果并与分析化学课本中的方法对比

4.1 数理统计方法的推导

设正态总体N(μ，σ2)，方差σ2已知，μ0为真值，μ为平均值，检验平均值与真值是否相等，即是否有系统误差。

假设:H0:μ=μ0，H1:μ≠μ0

则有N(μ0，σ2)。令:

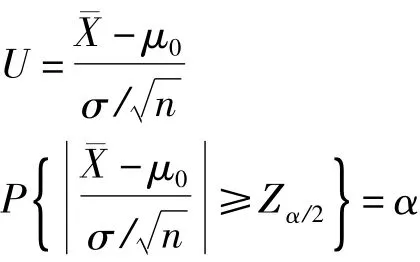
其中，α为显著水平。

当方差σ2未知时，同理可得:

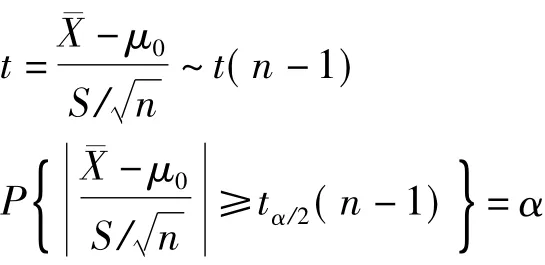
4.2 通过分析化学课本中的例题来验证

例:一种新方法用来测定试样含铜量，用含量为11.7mg/kg的标准试样，进行5次测定，所得数据为10.9，11.8，10.9，10.3，10.0，判断该方法是否可行?(置信度为95%)

解:假设:H0:μ=11.7;H1:μ≠11.7。

因为置信度为95%，n=5，则α=0.05，由表1可得tα/2(n－1)=t0.025(4)=2.7764。

所以

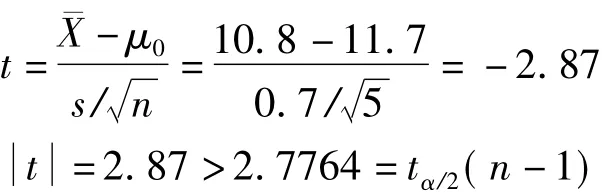
所以拒绝H0，即该方法不可行。

5 总结

综上可以看出，分析化学中数据处理的许多知识都可以用概率论与数理统计来解释和处理。虽然有时概率论与数理统计的方法很麻烦，但是它从本质上讲述了问题的过程，让我们能够更深入地理解和掌握其知识点。本文只是抛砖引玉，还有许多知识可以用概率论与数理统计方法来解决，有兴趣的同学可以更深入地探讨。从本文也可以看出学科之间的交叉学习对理解和掌握知识有很大帮助。

［1］ 肖筱南，茹世才，欧阳克智，等.新编概率论与数理统计.北京:北京大学出版社，2001

［2］ 华东理工大学化学系，四川大学化工学院.分析化学.第5版.北京:高等教育出版社，2003