再谈什么是活化能
——Arrhenius活化能的定义、解释、以及容易混淆的物理量
2010-07-02罗渝然俞书勤张祖德姚天扬高盘良
罗渝然俞书勤张祖德姚天扬高盘良
(1中国科学技术大学化学与材料科学学院 安徽合肥230026;2南京大学化学化工学院 江苏南京210093;3北京大学化学与分子工程学院 北京100871)
知识介绍
再谈什么是活化能
——Arrhenius活化能的定义、解释、以及容易混淆的物理量
罗渝然1俞书勤1张祖德1姚天扬2高盘良3
(1中国科学技术大学化学与材料科学学院 安徽合肥230026;2南京大学化学化工学院 江苏南京210093;3北京大学化学与分子工程学院 北京100871)
介绍IUPAC(1996)推荐的活化能定义,它源于反应速率常数与温度关系的Arrhenius图。对基元反应,活化能的Tolman解释最准确;对总包反应,活化能仅是表观量。以基元反应D+ H2为例,强调了活化能与许多相似物理量的区别。在较宽温度范围内,该Arrhenius图是弯曲的,这表示反应活化能随温度而变化。讨论为什么少数基元反应的活化能可能是负值甚至是零。
中学、大学与研究生用的化学参考教材中,活化能是出现频率很高的科学术语之一。但是,什么是活化能?不少国内大学教材和教学参考资料仍在使用不准确的文字。下面,我们将再次介绍有关Arrhenius活化能的定义、解释、以及很容易与活化能混淆的若干概念。此外,还讨论了非Arrhenius行为和负温度效应等。
1 简单的Arrhenius方程与活化能的准确定义
温度对许多化学反应速率有非常大的影响。1889年,瑞典科学家S.A.Arrhenius在研究蔗糖水解的速率与温度的关系时,受van't Hoff类似工作的启发,用速率常数k的自然对数ln k对温度的倒数1/T作图,得到一条直线。在科学文献上,ln k(或log k)对1/T作图,简称Arrhenius图。Arrhenius图上的线性关系可表示为:

引入气体常数R,可将这样的线性关系改写为:

或

上面的经验表达式(2)和(3),都称Arrhenius公式,它包括2个重要的经验参数A和Ea,这2个经验参数通称Arrhenius参数。其中参数A称为A因子(或指前因子),与速率常数k有相同单位,它来自Arrhenius图上的截距。Arrhenius把由图上斜率导出的能量因子Ea称为“活化热”,后来被科学文献改称为Arrhenius活化能。按照IUPAC(1996)推荐的观点[1],活化能Ea的准确定义是Arrhenius图上该直(曲)线在温度T下的斜率[1]:

从活化能的定义(式(4))看,反应温度T升高,速率常数k相应增加,活化能Ea必为正值。我们称它为正温度效应。绝大多数化学反应呈正温度效应。反之,称为负温度效应,对应于负活化能(见本文第5节和图3)。实验发现,在极少数情况下,某一很小的温度范围内,温度升高或降低,反应速率常数不变化,这对应于零活化能(见图3)。
基元反应的Arrhenius图中的速率常数k可从实验获得,也可按反应速率理论计算。因此,既可利用测量的k(T)数据得到基元反应的活化能,也可按反应速率理论计算的k(T)数据得到活化能(见本文第3节)。目前,国内某些大学教材和教学讨论文章还未接受IUPAC (1996)推荐的观点,赋予化学反应活化能以另外的定义,错误地认为从量子理论或某些理论可直接计算出活化能。
2 基元化学反应的Arrhenius活化能的最合理解释
Arrhenius经验式的提出,标志了定量的化学反应动力学诞生。100多年来,大量的实验发现,Arrhenius经验公式有很强的预测能力。从化学反应的3个层次看[2-7],在宏观(总包和基元)层次上研究化学反应,经常可绘出Arrhenius图,采用Arrhenius活化能的概念,如表1所示。这是因为,只要化学反应速率受温度影响,就可作Arrhenius图,确定某温度T下的斜率,即活化能Ea值。
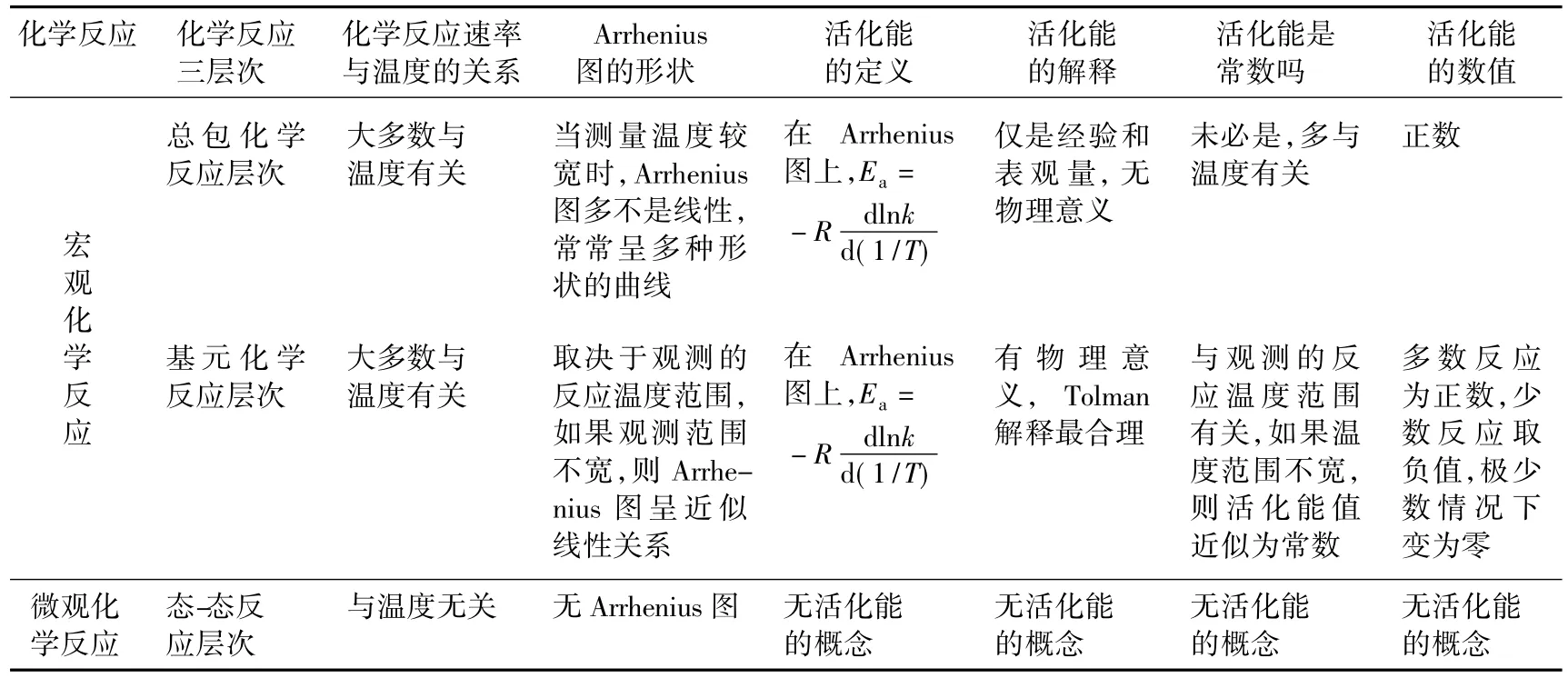
表1 化学反应三层次与活化能概念的适宜范围
活化能Ea位于Arrhenius公式中的指数项,因此活化能数值的改变,对化学反应速率常数有极大的影响,远比A因子的影响强烈。例如,常温条件下,活化能每改变5.7kJ/mol,反应速率常数将变化一个数量级。
对于如何理解Arrhenius活化能以及它有什么深入的物理意义,是100多年来人们一直感兴趣的科学问题。科学家的长期努力,已促进了若干化学速率理论的诞生。随着科学的进步,对基元反应活化能的理解历经了如下主要观点的变迁[8]:
①活化能是由非活化分子转变为活化分子的能量(Arrhenius);
②具有完成化学反应最小的、必须的能量(Lewis);
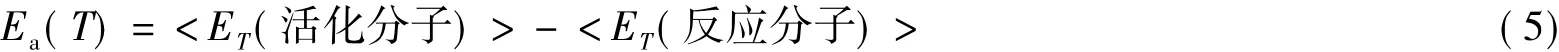
③在反应温度T时,全部活化分子的平均能量与全部反应物分子平均能量之差(Tolman),即:这里,对称符号<>表示对其中的物理量取统计平均。以上3种解释中,Tolman从统计力学提供的解释最准确、最合理[1-8]。虽然Tolman的论述发表在20世纪20年代,但长期没有得到人们的足够关注。到20世纪70年代,随着分子反应动态学(或微观化学动力学)的兴起和发展,国内外化学教材开始广泛传播Tolman的统计观点。Tolman解释有最清晰的物理意义,是因为人们观测到的基元化学反应都是一大群分子统计平均的结果,科学家还不能测量仅仅一个分子的行为。
正如表1强调的,在总包化学反应的层次上(如燃烧和爆炸、热裂解、多相催化、酶催化、有机物氧化或卤化、聚合反应等),当测量温度比较宽时,Arrhenius图多不是线性,常常呈多种形状的曲线[4]。按活化能定义(式(4)),它必然不是一常量,随温度变化。并且,这时候得到的活化能数值仅是经验和表观量,没有物理意义。这样情况下,如果把表观活化能叫E因子,也许会减少混淆。同时,表1还指出,Arrhenius图与活化能的概念不适合态-态反应。因为,在态-态反应层次上,没有热力学温度T的概念[8]。
大学教材在介绍化学反应的3个不同层次之后,不仅可以理解Arrhenius方程的局限性(A和Ea未必是常数,取决于反应温度范围),而且可以认识质量作用定律的局限性(不能用于总包反应,仅适合基元和态-态反应)。
3 Arrhenius活化能与反应能(位)垒、Eying理论的活化焓、活化内能、态-态反应的临界(阈)能等的严格区别
在化学文献中,反应势能面上的能(位)垒、Eying理论的活化焓、活化内能、态-态反应的临界(阈)能等是经常与Arrhenius活化能混淆的物理量。Pacey[9]用图示(图1)说明了这些物理量之间的区别。

图1 几个容易与Arrhenius活化能混淆的物理量[9]
只有严格区分这些相似的物理量,化学反应动力学的研究及其教学才是严格和清楚的。表2给出了全部7个物理量的定义、特点和取值范围。在阅读图1时,要注意哪些量是0 K时的物理量,哪些量与热容和温度的变化有关。在理解图1和表2时,特别要注意4点:
①经典能垒和量子能垒之间有区别。从经典能垒到量子能垒,要对反应物和活化络合物分子作零点能修正。量子化学计算出的势能面和能垒高度仅是0K时的值。在0K时分子没有平动能,没有碰撞,没有化学反应,势能面上的能垒不等同于实际化学反应的活化能。
②活化焓与活化内能之间有区别。对1mol理想气体,其差异是气体做的功pV=RT(图1),在室温条件下,它等于2.5kJ/mol。
③对于室温(或另外温度T)下的化学反应,在考虑0K时的量子修正之后,还要分别对反应物和活化络合物作从0K到实际温度T的热容变化的修正项(∫CVd T)。
④阈(临界)能是实验(如交叉分子束技术)可观测到的微观量,是分子水平上的量,与热力学温度T无关。阈能是发生反应性碰撞时分子必须具有的最低能量,它表明反应途径上有能垒。对于隧道效应较明显的化学反应,阈能为零。
以基元反应D+H2(DH+H为例,Pacey[9]给出了能垒(经典或量子)、阈能(理论或实验)、过渡态理论中的能量参数(活化焓或活化内能)等与该反应活化能之间在数值上的区别。它们列在表2的最后一行,能量单位是kJ/mol。
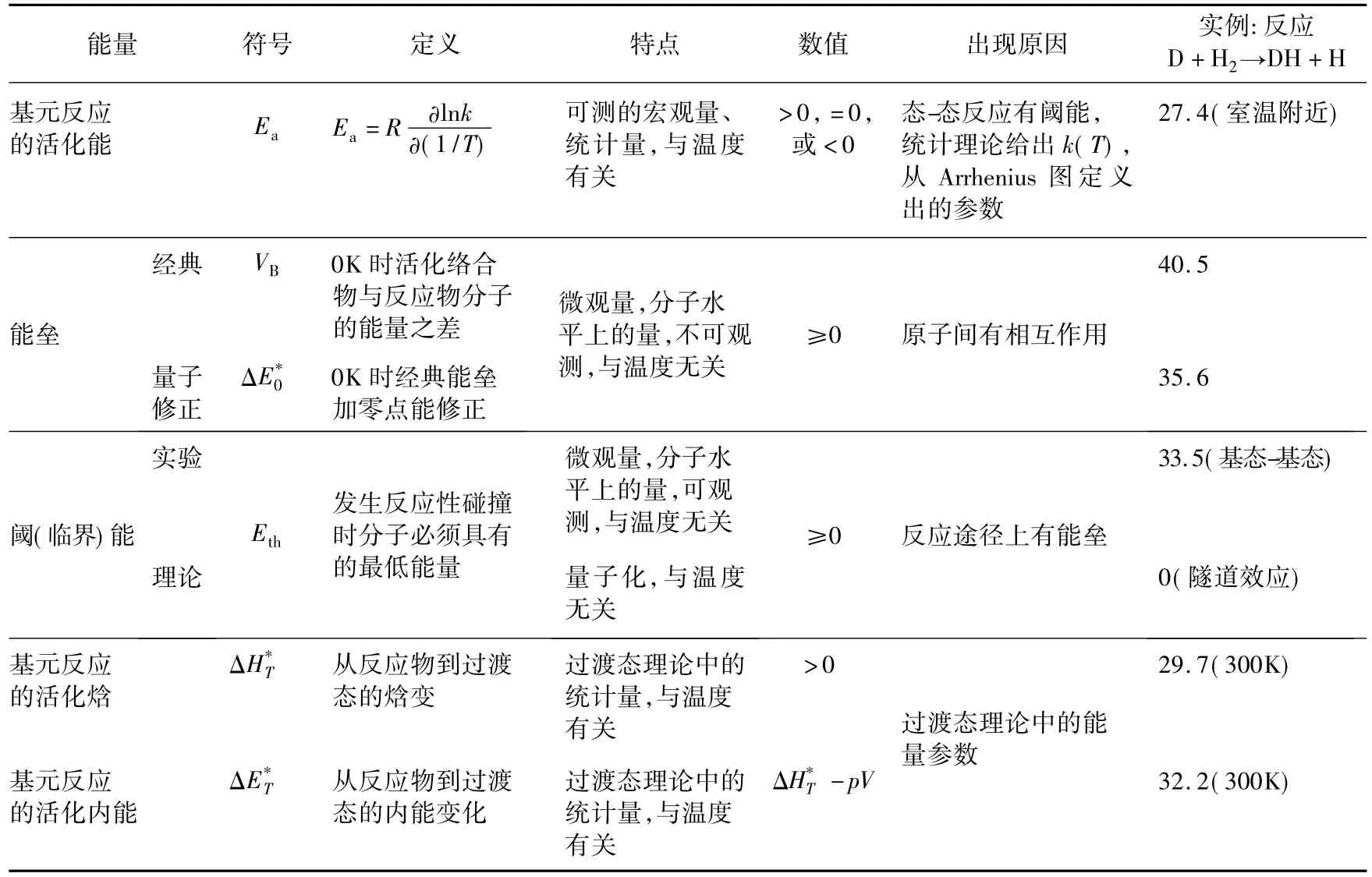
表2 几种容易与Arrhenius活化能相混淆的物理量(能量单位k J/mol)
反应势能面上的能(位)垒、Eying理论的活化焓、活化内能、态-态反应的临界(阈)能等与Arrhenius活化能有本质上的区别,但也有联系。一般地说,通过统计理论,利用微观的能垒和阈能等参数,可推导出该基元反应在不同温度下的速率常数k(T),作Arrhenius图,就可估算出活化能等Arrhenius参数。过程如下:

在有关理论(例如过渡态理论)的骨架下,在计算了该基元反应不同温度下的速率常数k(T)后,作Arrhenius图,也可得到活化能等Arrhenius参数。

如果读者对上述理论有兴趣,可阅读参考文献[2-4]。针对目前国内大学教材中的现况,下面再补充3点:
①利用过渡态理论可直接计算活化能吗?目前已发表了许多基元化学反应速率理论,至少已有20多种。甚至过渡态理论也有10多种,它们早已有别于20世纪30年代的传统过渡态理论。所有的反应速率理论都是建立在某一势能面上,然后用不同的统计方法,计算基元反应在不同温度下的速率常数k(T)。只有作Arrhenius图后,才能确定该基元反应的活化能。换句话说,任何反应速率理论(包括种种过渡态理论)都不可能直接计算出活化能。
②实验活化能与理论活化能有什么区别?按IUPAC(1996)推荐的观点[1],活化能的正确理解仅来自Arrhenius图的斜率(即式(4)),如果Arrhenius图中的k(T)来自实验,就可称它为“实验活化能”;如果Arrhenius图中的k(T)来自反应速率理论计算,可称它为“理论(或计算)活化能”。此外,不少化学文献借助于分子模型和几条理论假设,避开研究反应速率常数k和温度T的关系,力图直接取得基元反应活化能的数值。这样得到的活化能数值,只能叫预测的(predicted)或估算的(estimated)活化能。换句话说,预测(或估算)的活化能与理论(或计算)活化能是两回事,在逻辑上和概念上不可混淆。
③表观活化能和基元反应活化能有什么区别?因为我们既可观测总包反应速率常数k随温度T的变化,还可测量基元反应的k(T)关系,故对这两种不同层次的化学反应,都可作ln k (T)-1/T图。从总包反应实验数据k(T)得到的活化能,就是“表观活化能”,它是一个表观量,没有物理意义。表2和式(5)指出,基元反应的活化能才具有明确的物理意义。
4 改进的Arrhenius方程、活化能的数值随温度变化
在Arrhenius研究蔗糖水解动力学的年代,测量的温度范围比较小。故在Arrhenius图上,二元线性回归方程(3)很成功,A因子与活化能Ea被认为是一常数。但是,如果观测的温度范围比较大时,通常三元回归方程才能提供较好的拟合:

或

式(6)和(7)都称为改进的Arrhenius方程。这里,A,A'和E'都是与温度无关的常数,Tref是参考温度,常设Tref=298.15K;n可以是正数、负数、整数或分数。注意,式(6)或(7)中的物理量E'不能理解为活化能,称它能量因子或E因子更妥当。把式(6)或(7)代入式(4),可得:

按式(8),Arrhenius活化能Ea与温度有关。下面举一例子。
在167~1980K的温度范围,Michael等[10]用闪光光解和激波技术观测了基元反应D+H2→DH+H的速率常数。他们在Arrhenius图上(图2)发现观测点可用改进的Arrhenius方程描述:
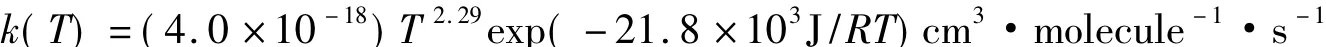
在NIST化学动力学数据库里(http://kinetics.nist.gov/kinetics),Michael等的结果被改写为:
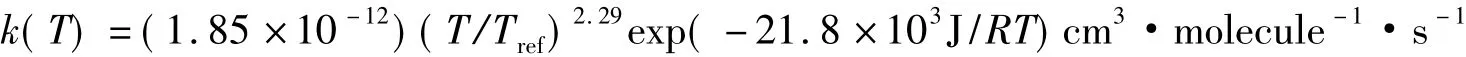
NIST数据库也用简单的Arrhenius方程回归了Michael等的结果,如图2所示。在图2中,弯曲线是改进的Arrhenius方程的拟合,直线是简单的Arrhenius方程的拟合。表3对比了这两种拟合结果。从均方根偏差看,用改进的Arrhenius方程拟合提供了很好的结果,其均方根偏差几乎为零。在科学文献中,把这样的关系叫非Arrhenius行为。大多数基元化学反应都呈现非Arrhenius行为。

图2 反应D+H2→DH+H的Arrhenius图[11]

表3 基元反应D+H2→DH+H速率常数的拟合(T=167~1980K)
Michael等[11]最近发现,在167~2112K温度范围内,为了得到最好的拟合,建议对于基元反应D+H2采用如下多项式:
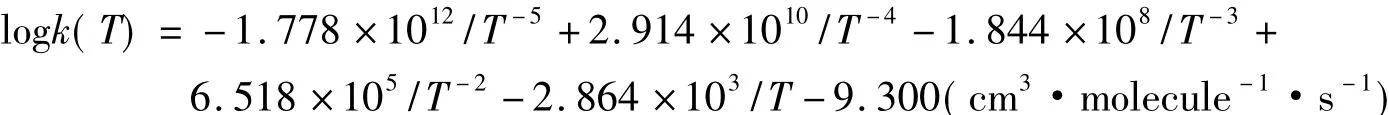
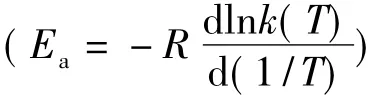
在某些情况下,改建的Arrhenius方程可能退化为:

这时,反应活化能可简单地估算:

5 基元化学反应的负温度效应与负活化能
Smith等[12]归纳了许多OH的夺H反应(OH+RH→H2O+R)的速率常数,他们发现,某些反应有负温度行为,即温度升高,速率常数降低,如图3所示。负温度效应已被许多科学家观测到。显然,负温度行为对应于负活化能。图3还表示,对于基元反应
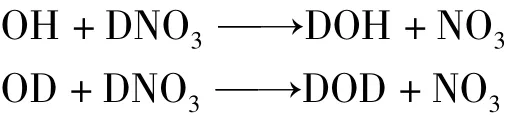
在高温区间(>300K),呈正活化能;在低温区间(<290K)时,呈负活化能;在一很小的温度区间(点),该反应的活化能是0(零活化能)。
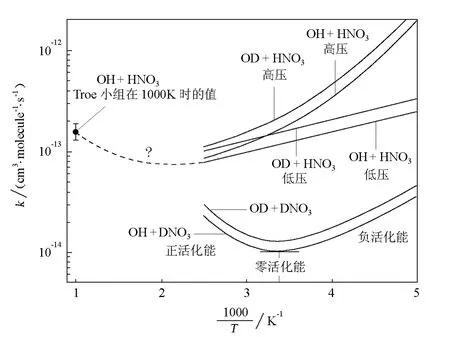
图3 某些OH夺H反应的Arrhenius图[12]
Smith等认为[12],该基元反应经历了氢键(缔合的中间)络合物(图4)。
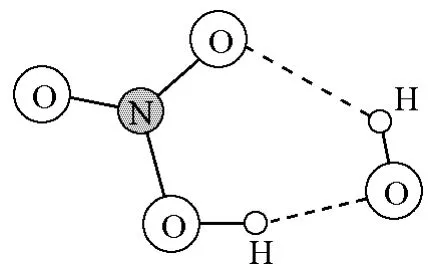
图4 OH夺H反应形成的氢键络合物
该氢键络合物的能量比反应分子的能量低,在势能面上出现一个“势阱”(如图5)。有负温度行为的许多基元反应的势能面都有类似的“势阱”。在态-态反应层次(表1),它们对应于长寿命络合物[4,8],不同于短寿命络合物的动力学特征。
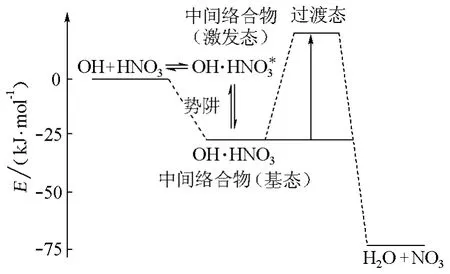
图5 OH+HNO3的反应机理与氢键(缔合的中间)络合物[12]
基元化学反应的负温度效应与负活化能的研究,使我们对化学反应的多样性和极其复杂性,有了更深入、更全面的认识。
6 建议和结束语
①大学教材应当与时俱进,接受IUPAC(1996)推荐的活化能定义,放弃其他陈旧的说法。
②物理化学教材应当严格区别Arrhenius活化能与反应能(位)垒、Eying理论的活化焓、活化内能、态-态反应的临界(阈)能等许多相似物理量。
③大学教材应当指出,Arrhenius图既可用2参数拟合(Arrhenius方程),也可用3参数拟合(改进的Arrhenius方程)。当实验温度的范围较宽时,改进Arrhenius方程拟合的均方根偏差最小。
④在物理化学教材中应当阐明,为什么基元反应的活化能不一定是常量,为什么少数基元反应的活化能可能是负值甚至是0。
[1] Laidler K J.Pure&Appl Chem,1996,68:149
[2] 俞书勤.微观化学反应.合肥:安徽科学技术出版社,1985
[3] 韩德刚,高盘良.化学动力学基础.北京:北京大学出版社,1987
[4] 赵学庄,罗渝然,臧雅茹,等.化学反应动力学原理(下).北京:高等教育出版社,1990
[5] 胡英.物理化学参考.北京:高等教育出版社,2003
[6] 范康年.物理化学.第2版.北京:高等教育出版社,2005
[7] 印永嘉,姚天扬.化学原理.北京:高等教育出版社,2006
[8] 罗渝然.化学通报,1981(4):50
[9] Pacey PD.JChem Educ,1981,58:612
[10] Michael JV,Fisher JR.JPhys Chem,1990,94:3318
[11] Michael JV,Su M C,Sutherland JW.JPhys Chem A,2004,108:432
[12] Smith IW M,Ravishankara A R.JPhys Chem A,2002,106:4798
