Kalman算法在原子时计算中的应用研究

李变，屈俐俐，高玉平



Kalman算法在原子时计算中的应用研究

李变1,2，屈俐俐1，高玉平1

（1. 中国科学院国家授时中心，西安 710600；2. 中国科学院研究生院，北京 100049）

为了寻求改进地方原子时算法的可能性，基于原子钟的离散动态模型，分析研究了Kalman滤波算法在地方原子时计算中的具体应用。采用中国科学院国家授时中心的18台铯原子钟数据，分别计算出基于ALGOS算法和经典Kalman算法的时间尺度。结果表明，两种时间尺度在性能方面极为相似，短期和长期频率稳定度相当。

时间尺度；Kalman算法；频率稳定度

建立一个稳定、准确、可靠的时间尺度，主要与参与守时的原子钟的性能和时间尺度算法有关。近年来，随着大量高性能原子钟进入各时频实验室，地方原子时尺度及国际原子时TAI的水平有了明显提高[1]。但是，国际电信联盟（ITU）仍然把原子时算法的改进作为其主要任务之一，并倡导各国进行研究，充分说明了算法的重要性。

时间尺度算法实质上就是研究原子钟之间的噪声关系，通过调整原子钟之间的相互关系，使最后计算得出的原子时的不确定性尽可能地小[2]。

最具有代表性的时间尺度算法是国际权度局BIPM时间部的ALGOS算法以及后来提出的Kalman算法。ALGOS算法属于经典加权算法，该算法的理论依据是频率稳定度表征理论[2]。根据这一理论，原子钟噪声是五种不同性质的随机过程的叠加。由于这样的噪声过程远比白噪声过程复杂，用标准方差来衡量噪声大小非常困难，所以，在频率稳定度表征理论中，用噪声幂律谱和Allan方差来描述各种噪声之间的强弱关系。也就是说，在Allan方差中，一定的取样时间对应着一定的噪声过程，因此，在经典加权平均算法中，若以Allan方差决定权重，则权重的大小主要与某一种噪声过程的强弱有关，而不论其他几种噪声过程如何。

针对以上问题，美国学者Barnes提出了原子时的Kalman算法[3-4]。本文基于原子钟的离散动态模型介绍时间尺度的Kalman算法，并采用中国科学院国家授时中心（NTSC）的18台铯原子钟的数据，对这两种算法进行了分析比较。

1 原子时的Kalman算法

时间尺度的Kalman算法完全放弃了权重概念，而是从估值理论的观点出发，对参考钟和理想时间之差做统计意义上的最优估计[3]。该算法对每一台原子钟建立一个由状态方程描述的噪声模型块，将2种或3种主要噪声过程分别在相位、频率和频率变化率3个层次上区分开来。钟与钟之间的噪声关系则通过每项噪声系数的大小反映出来。Kalman滤波器的输入量是钟组内各钟与参考钟的钟差测量值，输出量是钟组内的所有钟的相位和频率估值。

1.1 Kalman算法的基本原理

原子时Kalman算法的基础是原子钟的离散动态模型[5]，将钟组内所有单台钟的模型叠加起来，就构成了钟组的Kalman滤波器。

设有台钟，均符合下述模型：

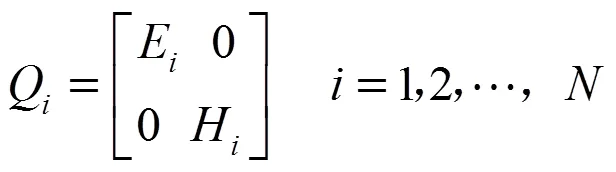
根据Kalman滤波原理，钟组动态模型为

式（3）中

在用Kalman滤波算法计算地方原子时时，设以（Kalman）和（）分别代表计算得到的地方原子时和第个原子钟，那么上面的表达式中的x()和y()则分别为时刻的（Kalman）与（）之间的相位之差和频率之差。测量方程为

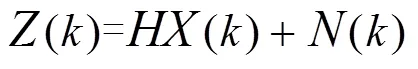
Kalman滤波方程组为：

式（5）中，为系统噪声矩阵，为的误差方差矩阵，为测量噪声矩阵。

1.2 Kalman算法中参数的确定

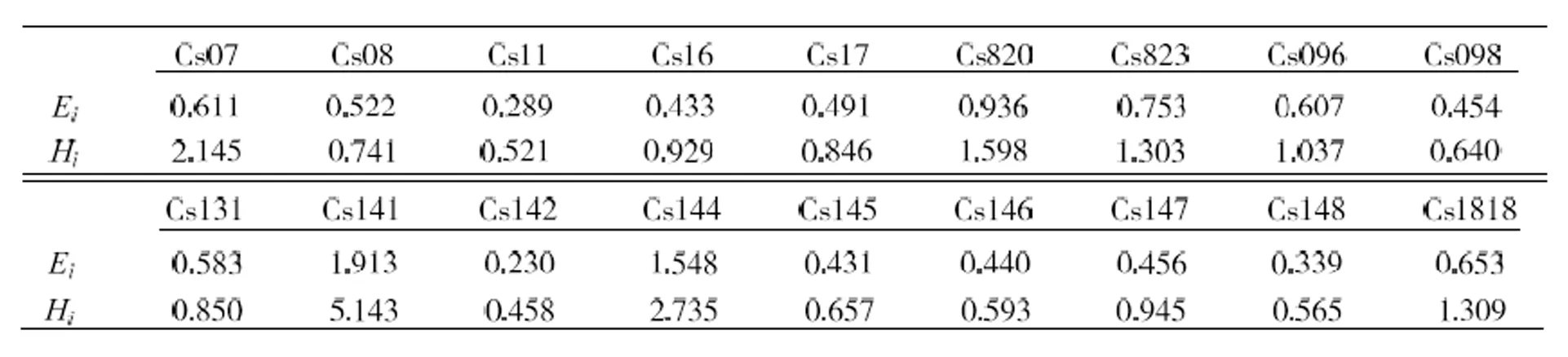
Kalman算法中的关键是确定系统噪声方差阵。如1.1节所述，系统噪声主要是指白色调频噪声和随机游走调频噪声。根据商品铯钟在平均时间间隔为1～10 d范围的情况下，主要表现为频率白噪声，以及在20～70 d范围的情况下，主要表现为随机游走频率调制噪声的特性，采用2008年这1年的NTSC原子钟比对数据，分别计算了每台钟对应的E和H，示于表1。

表1 NTSC各钟的E和H

2 实验分析

采用2008年6月至2009年5月在中国科学院国家授时中心时间频率基准实验室运行的18台HP5071A铯原子钟的比对数据，根据公式（5），计算得到用Kalman算法计算的时间尺度（Kalman）。（Kalman）和（ALGOS）（采用ALGOS算法计算的时间尺度）分别相对于的相位差及速率（日差）波动，如图1和图2所示。此外，利用由时域分析所得的表征原子钟稳定度的Allan方差，比较了（Kalman）和（ALGOS）的稳定度情况，示于图3。

图1 2种算法得到的时间尺度的相位差

图2 2种算法得到的时间尺度的日差

图3 2种算法得到的时间尺度的Allan方差

3 Kalman算法的稳定性分析

如果（5）式所表达的Kalman滤波器是稳定的，则从Kalman滤波器得到的状态估计具有最小均方误差。然而，根据系统的可观性定义与滤波器稳定性定理[6]，及时间尺度Kalman算法的原理可知，原子时的Kalman算法所构造的系统不完全可观，因而导致滤波器发散。在这里，系统的不完全可观性可从代数学上解释，即试图从-1个独立方程中解出个独立的未知数，这显然是不可能的。

Kalman滤波器发散，意味着估值结果的误差随时间无穷增大，表现在滤波器上就是滤波误差阵和预测误差阵的增大。为了清楚地看到Kalman算法的发散性，图4给出了54 619～54 979 期间（Kalman）与（ALGOS）相对于国际原子时的相位差。

图 4（Kalman）与（ALGOS）相对于的相位差

由图4可看出：在54 619～54 819期间两种算法的结果相当，而在54 819以后-（Kalman）明显偏离了-（ALGOS）。这是由于原子时Kalman算法的输入是-1个测量值，而输出是个估计值，因此导致Kalman估值结果的误差随时间无穷增大。

4 结语

本文采用NTSC的18台铯原子钟的比对数据，分别实现了地方原子时的ALGOS算法和Kalman滤波算法。实验结果表明，应用Kalman算法得到的时间尺度（Kalman）与用ALGOS算法得到的时间尺度（ALGOS）在结果及其性能方面极为相似，两者的长期和短期稳定度相当。但是，Kalman滤波算法的不完全可观性会导致估值结果的误差随时间无穷增大。因此，在应用Kalman算法时，必须考虑Kalman算法的发散性问题，合理选择估值区间。

[1] THOMAS C. Stability and Accuracy of International Atomic Time TAI[C]//European Frequency Time Forum. [S.l.]: [s.n], 1996, (5-7): 520-527.

[2] 卫国. 原子钟噪声模型分析与原子时算法的数学原理[D]. 西安: 中国科学院陕西天文台, 1991.

[3] BARNES J A, CHI A R, CUTLER L S, et al. Characterization of Frequency Stability[J]. IEEE Transactions on Instrumentation and Measurement, 1971, IM-20(2): 105-120.

[4] BARNES J A, JONES R H, TRYON P V, et al. Stochastic Model for Atomic Clocks[C]//Proceeding of the 14th Ann. Precise Time and Time Interval(PTTI) Appl. [S.l.]: [s.n], 1992: 295-306.

[5] 尹东山, 高玉平, 陈鼎, 等. 基于脉冲星的星载钟时间修正算法研究[J]. 时间频率学报, 2009, 32(1): 43-49.

[6] 宋文尧, 张牙. 卡尔曼滤波[M]. 北京: 科学出版社, 1991: 112-116.

Application of Kalman Algorithm to Atomic Time

LI Bian1,2, QU Li-li1, GAO Yu-ping1

(1. National Time Service Center, Chinese Academy of Sciences, Xi’an 710600, China;2. Graduate University of Chinese Academy of Sciences, Beijing 100039, China)

In order to seek for the possible way to improve the algorithm for local atomic time, the application of Kalman algorithm to atomic time is studied based on the discrete and dynamic model of atomic clocks. The time scales(ALGOS) and(Kalman) are calculated with ALGOS and Kalman algorithms respectively by adopting the data of the 18 cesium clocks operated at the National Time Service Center, Chinese Academy of Sciences. The results show that the performances of the two timescales are similar, i.e., they are equivalent in short-term and long-term stabilities.

time scale; Kalman algorithm; frequency stability

P127.1+2

A

1674-0637(2010)01-0011-05

2009-11-23

国家自然科学基金资助项目（10573019）；中国科学院知识创新工程重要方向资助项目（KJCX2-YW-T12）

李变，女，博士研究生，主要从事时间频率方面的研究。