基于ANSYS的接触网弹性计算
2010-06-27郝方涛吴积钦
郝方涛,吴积钦
0 前言
接触网是一个三维架空的机械系统,当接触线受到抬升力作用时,会产生相应的抬升量,单位力的作用产生的抬升量即为“弹性”。
接触悬挂的弹性不仅反映了接触网设计的好坏,还对受电弓与接触网间的接触质量有直接的影响,是评价弓网受流质量的一个重要因素。随着机车速度的不断提高,较大的弹性不均匀度会使接触网振动加剧,增大离线率,从而破坏受流。在接触网的设计、施工中应严格控制弹性不均匀系数。本文利用有限元理论,建立了简单链形悬挂和弹性链形悬挂的有限元模型,对一个跨距内的接触网弹性进行了仿真计算,对弹性的变化规律做了定量分析,这对今后的接触网设计有重要的指导意义。
1 接触网仿真模型的建立
接触网是沿线路布置的架空的悬索结构,随着跨距的变化,其弹性亦会发生相应的变化,这与接触网的参数设置以及吊弦的布置情况都有密切关系。对于不同的跨距和接触网线材参数,应建立相应的模型,才能精确地计算出该情况下的接触网弹性变化情况。
本文在建立相应的仿真模型方面做了以下几种假设:
(1)承力索、接触线、弹性吊索和吊弦为柔性索,仅能承受沿其轴向的拉力。
(2)定位器被等价为1根带拉应力的吊弦。
(3)不考虑接触网内的张力差。
接触网模型的建立思路:对接触网进行几何求解分析,建立接触网的关键点,继而连线构建接触网的几何模型。把线索上的张力换算成应变,对建立的几何模型进行网格划分和边界条件约束,进行空载时的接触网模型迭代,直到所建立的模型达到平衡为止。
1.1 定位器的受力分析
以 O点为支撑点对定位器进行受力分析(如图1),建立其力矩平衡方程:
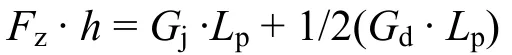
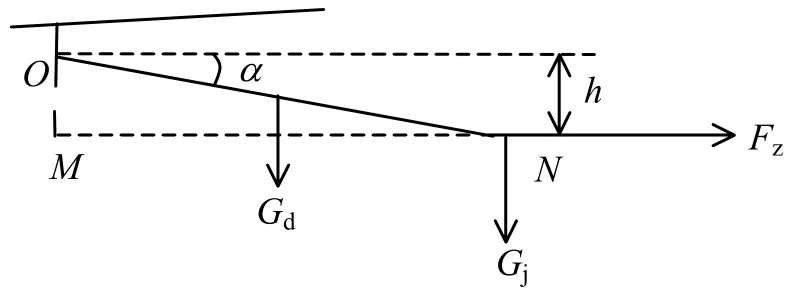
图1 定位器受力分析图(正定位)
求解上述平衡方程则得
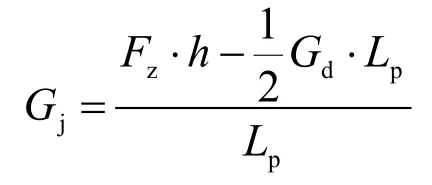
式中,a为定位点处的拉出值;L1,L2为左右2个相邻跨距的取值;F为接触线张力。
1.2 简单链形悬挂模型的建立
为了更好计算接触网定位点处的弹性值,建立了三跨简单链形悬挂模型,选择中间的一跨作为研究对象,为此把定位器等效为1根带张力的吊弦,定位器的竖向力换算成此时线索上的应变,建立简单链形悬挂的模型,如图2所示。

图2 简单链形悬挂几何模型图
其中,中间跨的跨距选择65 m,第1根吊弦和最后1根吊弦距离定位点5 m,跨内的7根吊弦均匀布置。
1.3 弹性链形悬挂模型的建立
弹性链形悬挂和简单链形悬挂的模型差不多,只不过在定位点的地方多出了1根弹性吊索,且跨距内的第1个吊弦和最后1根吊弦都是直接连接到弹性吊索上的。弹性链形悬挂模型如图3所示。

图3 弹性链形悬挂几何模型图
其中,中间跨的跨距选择65 m,弹性吊索选择18 m,第1根吊弦和最后1根吊弦距离定位点5 m,其他5根吊弦均匀布置。
2 接触网的弹性计算
2.1 仿真参数设置
本文采用LINK10单元模拟所有线索,根据线索参数的不同,建立不同的实常数和材料特性,对已建立的接触网几何模型进行网格划分和边界条件约束。
各线索的基本参数设置见表1。

表1 接触网线索基本参数设置表
由于吊弦所悬吊的接触线长度不一样,而且根据第1.1节所计算得到的等效吊弦上的张力也不一样,所以吊弦的张力要分别进行计算得到。
把线索上的张力换算为单元的应变,等价吊弦的应变值为σ1= Gj/ EA(E为材料的弹性模量,A为吊弦横截面积)。
其他线索上的应变值:σ2= N / EA(N为线索张力)。
2.2 简单链形悬挂的弹性计算
计算方法:在所建立的简单链形悬挂模型上施加集中力,通过10次的迭代求解最终得到准确的抬升量,进而得到该节点处的接触网弹性值。
在各个吊弦点施加集中力,得到的仿真结果见表2。
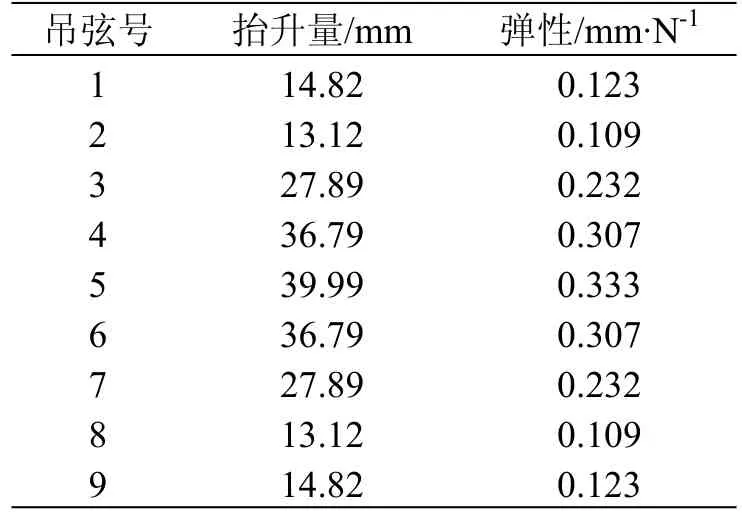
表2 简单链形悬挂仿真结果数据表
跨距内的最大弹性为ηmax= 0.333 mm / N。
弹性不均匀度为
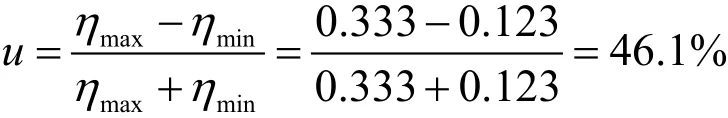
由表 2可以直观地绘制出简单链形悬挂弹性在跨距内的变化规律图(图4)。
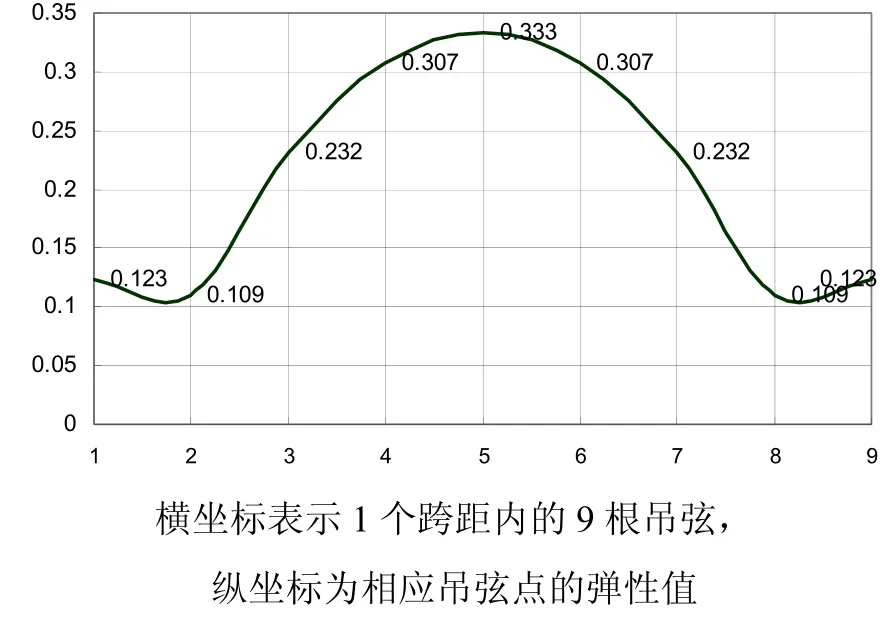
图4 简单链形悬挂的弹性变化曲线图
2.3 弹性链形悬挂的弹性计算
在弹性链形悬挂模型各个吊弦点施加集中力,通过仿真求解得到的结果见表3。
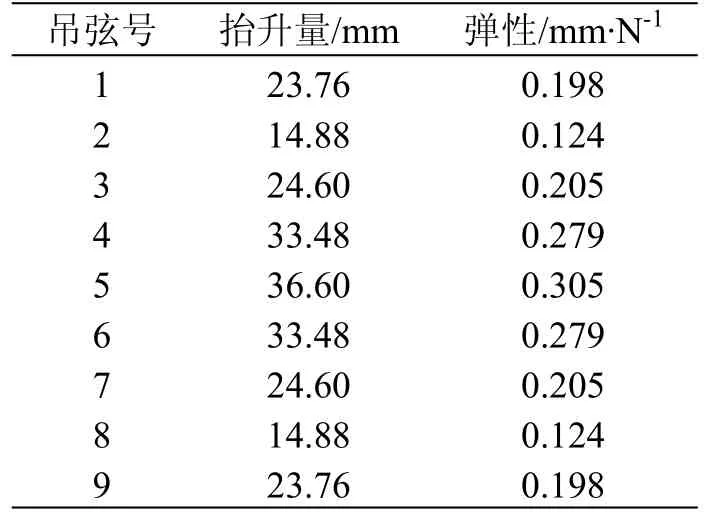
表3 弹性链形悬挂仿真结果数据表
跨距内的最大弹性为ηmax= 0.305 mm / N。
弹性不均匀度为
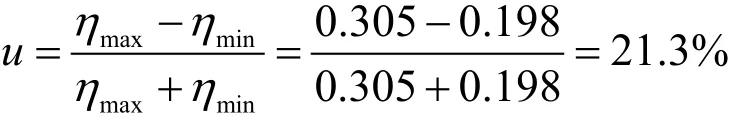
由表 3可以绘制出简单链形悬挂弹性在跨距内的变化规律图(图5)。
3 结论
本文建立了接触网 2种悬挂模式的有限元模型,仿真分析得到了跨距内的弹性大小及变化规律,通过对简单链形悬挂和弹性链形悬挂的对比分析,可以得到如下结论:同样跨距情况下,简单链形悬挂的弹性不均匀度大,弹性链形悬挂由于在定位点处增加了弹性吊索,改善了定位点的弹性状况,使得一个跨距内的弹性不均匀度减小,更加适合列车高速运行的要求。
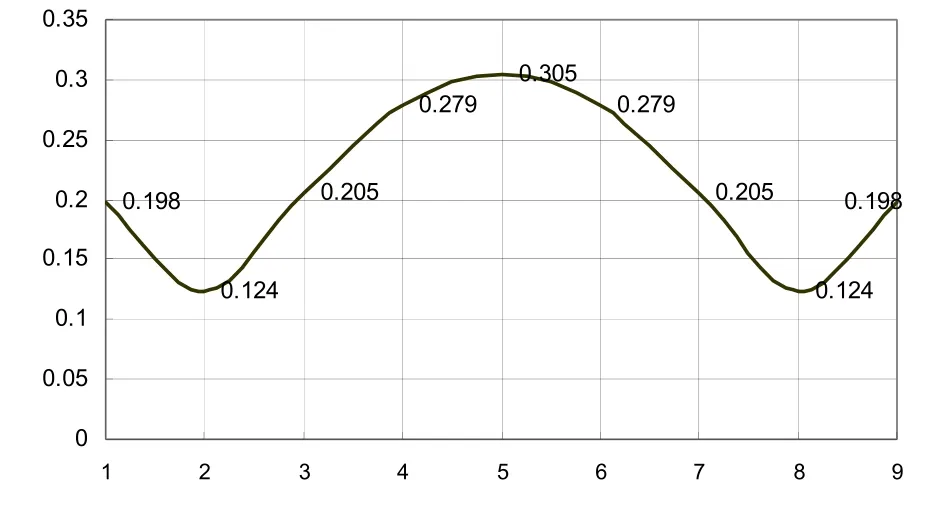
图5 弹性链形悬挂的弹性变化曲线图
4 存在问题及改进建议
本文建立的接触网模型把定位器等效为 1根带张力的吊弦,该假设限制了定位点处接触线的竖向运动,对接触网的动态仿真有很大的局限性,且通过仿真得到弹性链形悬挂的跨中弹性比简单链形悬挂的小,这与理论研究结果不符,所以在模型建立以及弹性吊索分析上均存在一些问题,需要做更深入的研究。
建议建立接触网的三维实体模型,对定位器不做假设处理,尝试接触线可否用梁单元模拟。
[1]Kießling, Puschmann, Schmieder.电气化铁道接触网[M].中铁电气化局集团译.北京:中国电力出版社,2004.
[2]于万聚.高速电气化铁路接触网[M].成都:西南交通大学出版社,2005.
[3]王洪林.接触网的弹性计算[D].西南交通大学硕士学位论文,2009.
[4]龚曙光.ANSYS基础应用及范例解析[M].北京:机械工业出版社,2003.
[5]任辉启.ANSYS7.0工程分析实例详解[M].北京:人民邮电出版社,2003.
[6]博弈创作室.ANSYS7.0基础教程与实例详解[M].北京:中国水利水电出版社,2003.
