一种基于Volterra级数的基带数字预失真

郑百衡

（中国西南电子技术研究所，四川 成都 610036）

1 引言

为充分利用有限的频谱资源，正交幅度调制（QAM）、正交频分复用（OFDM）等高效调制方式都将被广泛采用。然而作为非恒包络调制技术，这些调制方式存在较大包络波动，对功率放大非线性十分敏感，会导致严重的频谱带外再生和带内失真，影响通信的质量，造成邻道干扰[1-2]。目前主要避免功率放大器非线性的办法是采用线性化技术，而数字预失真技术是最有前景及有效的一种线性化方法。由于功率放大器的特性会随着时间、温度、环境以及信号本身的变化而变化，因此还需要采用自适应技术，使预失真装置能够自适应跟踪放大器特性的变化。

2 数字预失真系统

预失真技术包括射频预失真、中频预失真和基带预失真3种方法[3]。射频预失真使用射频非线性器件进行校正，对其控制和调整较困难，频谱再生分量改善较少，高阶频谱分量抵消困难，线性指标低；中频预失真的核心部分采用数字部件进行非线性和自适应控制，而采用模拟电路在中频部分实现预失真；基带预失真在基带处理可以通过DSP实现预失真器，相对于中频系统硬件电路简单且便于数字信号处理算法实现，是目前广泛使用的预失真技术。

数字预失真（Digital Pre-Distortion，DPD）的基本原理是在信号进入功放前先进行非线性变换，这种变换特性与功放的非线性特性互补，从而使得功放输出信号呈现为调制信号的线性放大，避免信号的带内畸变和带外频谱再生。实际的预失真器是预失真训练器的1个拷贝。图1描述了数字预失真网络的等效基带模型框图，由图可知DPD的目标就是找到信号的变换，使它与非线性PA级联产生1个无失真系统。图中G代表功放的增益。

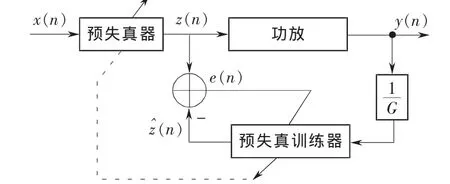
图1 DPD电路的基带等价模型

3 记忆多项式模型

在宽带和/或高功率应用中，DPD模型和结构必须能够补偿PA的记忆效应以及非线性。Volterra级数模型常常用来表示PA的记忆非线性。但是Volterra级数需要太多的系数以至于在实际应用中不可用，现实中通常采用简化的Volterra级数来建模[1-2]。

Volterra级数模型是非线性系统使用最广泛的模型。因为经典的线性自适应滤波方法可容易地推广到这种模型，使得其适用于非线性自适应滤波[4]。非线性系统的Volterra级数输出信号与输入信号的关系为

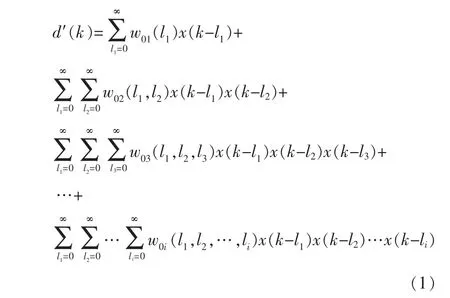
式中：i=0，1，…，∞；w0i（l1，l2，…，li）是基于 Volterra 级数的非线性滤波器模型的系数，也称为系统的Volterra核。记忆多项式模型采用简化的Volterra级数，如式（2）所示

式中：K是非线性阶数，Q代表PA的记忆长度。在这里为了在保持可接受性能的同时减少实现的复杂性，模型中只保留了非线性的奇数项，这样的折中使复杂程度得到了40%的减少，代价是3～5 dB的频谱再生。基带模型含偶数项的好处在文献[5]中有详细的论述。

4 PA模型

在基于多项式失真理论研究中，确定功放的多项式模型十分重要。随着通信信号带宽的增加，功放逐渐表现出记忆性。对于有记忆多项式提出了很多模型，Volterra级数是常用的描述非线性特性的模型，但其计算复杂度随多项式阶数及记忆深度呈指数上升，由此提出了简化的有记忆多项式模型，如：Wiener模型、Hammerstein模型、Wiener－Hammerstein模型和记忆多项式模型等[5]。应用中记忆型功放模型采用Wiener模型。这个系统由一个LTI子系统H（z）级联一个无记忆非线性子系统F（v）组成，如图2所示。

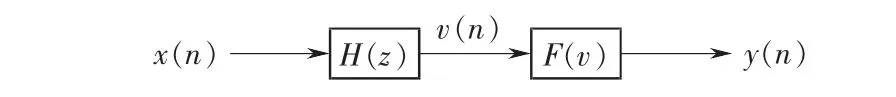
图2 Wiener系统PA模型

5 Volterra RLS算法

构建有记忆结构的DPD有2种方法。一种是先辨识PA然后求PA的逆，然而获得有记忆非线性系统的逆通常是很困难的。另一种方法是使用间接学习结构来直接设计DPD，它消除了模型设计和参数估计的需要。间接学习结构的框图也如图1所示。反馈路径为预失真训练器，其输入为 y（n）/G，（n）是它的输出。 实际的预失真器是预失真训练器的一个拷贝，其输入为x（n），输出为z（n）。 目标是使 y（n）=G·x（n），这样有=z（n）和 e（n）=0。 给定 y（n）和 x（n），当被最小化时若达到设定值则算法收敛，此时得到DPD的参数。

DPD电路的初始化执行最优滤波，在实现中由离线计算来实现。自适应滤波的系数估计可以考虑为线性优化任务。可以使用任何普通的估计算法，如MMSE、维纳滤波、RLS等。这些算法都试图解决一个线性优化问题，也就是线性参数估计。使用这些算法得到的稳定点可能会有很大的不同，主要原因是这些算法使用的误差准则不同，从而导致误差性能曲面不同。

应用中预失真算法的仿真采用Volterra RLS算法。RLS算法流程[6]如下：

1）初始条件为 w（0）=x（0）=0，C（0）=δ-1，δ为小的正实数运算，n=1，2，…。 其中 w（）是滤波器系数，x（）是输入信号，d（）是期望信号。

2）取得 d（n），x（n）。

3）更新增益矢量

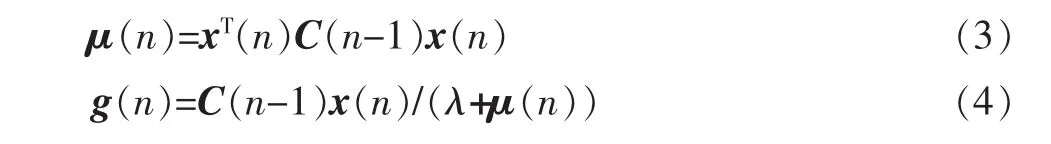
4）更新滤波器参量

5）更新逆矩阵

根据图 1 和式（2），可以得到 x（n）（不失一般性，这里公式中省略了G）

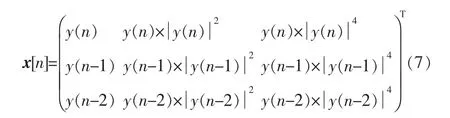
6 Matlab仿真

在仿真中随机生成源数据，加噪后经过成型滤波送入预失真器，调制方式采用QPSK。注意自适应算法需要期望数据和滤波器输出位置对齐，否则算法无法收敛。这就必须知道从功放返回后的数据与发送数据之间的延时。应用中通过在随机数据前面插入具有良好的自相关特性的同步头，采用检测同步头相关峰的方法测出这个延时。

使用 Wiener系统的 PA模型中H（z）和y（n）的表达式选择如式（8），式中 v（n）和 y（n）是无记忆非线性系统 F（v）的输入和输出。基于AB类PA的系数b的实测值在式（9）中给出[5]，即

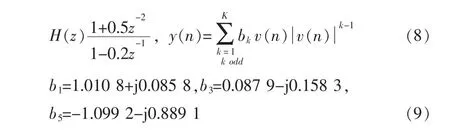
Volterra RLS算法的滤波器阶数取9阶、步长delta=0.001，放大器增益G=15时，输出频谱如图3所示，其中虚线为成形后基带信号频谱（最下面的频谱）；实线为通过PA模型后频谱（最高处频谱）；点划线是采用DPD后的输出频谱。该预失真器能够有效地校正由于功率放大器的非线性和记忆效应引起的信号失真。

图3 线性化性能比较

[1]SAFARI N，ROSTE T，FEDORENKO P，et al.An approximation of volterra series using delay envelopes，applied to digital predistortion of RF power amplifiers with memory effects[J].IEEE Microwave and Wireless Components Letters，2008，18（2）：115-117.

[2]ZHANG Peng， ZHANG Qin， WU Siliang.A novel adaptive digital predistortion for RF power amplifier linearization based on simplified volterra series[C]//Proc.IEEE 2007 International Symposlum on Microwave，Antenna,Propagation and EMC Technologies for Wireless Communications.[s.l.]：IEEE Press，2001：2-3.

[3]吕卫，索召和.数字电视发射机技术及应用[J].电视技术，2008，32（8）：8-13.

[4]DINIZ P，Sr.自适应滤波算法与实现[M].2版.刘郁林，景晓军，谭刚兵，等译.北京：电子工业出版社，2004.

[5]DING L.Digital predistortion of power amplifiers for wireless applications[D].Georgia∶Electricaland ComputerEngineering Georgia Institute of Technology，2004.

[6]HAYKIN S.自适应滤波器原理[M].郑宝玉，译.北京：电子工业出版社，2003.