正弯静叶和直叶静叶透平级气动性能的对比分析

王建录, 孔祥林, 刘网扣, 崔 琦, 张兆鹤

(1.东方汽轮机有限公司,德阳618000;2.上海发电设备成套设计研究院,上海200240)

符号说明:

η′u — — 轮周效率η′*u ——滞止轮周效率Nw——水力测功器吸收的功率,kW N′u— —轮周功率,kW Nx——空转功率,kW G——级流量,kg/s

H0——级的等熵焓降,kJ/kg——级的等熵焓降与级的轴向排气损失之差,kJ/kg C2z——动叶出口平均轴向速度,m/s H*0 i*0——级前滞止焓,kJ/kg i2s——级后等熵焓,kJ/kg u——动叶根部直径处的圆周速度,m/s p*0——级前总压,Pa——级前总温,K F1——静叶出口喉部面积,m2 μ1——静叶流量系数p1r——静、动叶间根部壁面静压沿一个栅距的平均测量值,Pa p1t——静、动叶间顶部壁面静压沿一个栅距的平均测量值,Pa T*0 μ——级流量系数p2r——级后根部壁面静压,Pa p2t——级后顶部壁面静压,Pa q——级折合流量q1——静叶折合流量ρr——根部反动度ρt——顶部反动度Co——级的理想速度,m/s

汽轮机效率与其通流部分的流动效率紧密相关.由于喷嘴与动叶的叶型损失、漏气损失以及二次流损失占总级损失的绝大部分(约为 80%～90%[1]),因此,研发透平叶栅的先进叶型并对其进行优化设计,尽量减少动、静叶的气动损失,具有重要的理论意义和应用价值.

影响叶栅性能的因素很多,除叶型、叶栅的几何参数及气动参数外,流道形状和叶片的成型也是十分重要的因素.目前,在通流设计中,正弯曲叶片等技术得到普遍的重视和应用,已经广泛应用在汽轮机上,实践证明取得了良好的效果[2].但由于其发展迅速,应用范围越来越广,提出了很多新的问题,其中一些问题不仅具有重要的学术价值,而且直接影响正弯曲叶片的进一步发展与推广[3-4].笔者对某汽轮机高压缸的正弯静叶级进行了模化的单级空气透平级性能试验与数值计算,并将正弯静叶改为相同叶型的直叶片静叶,进行了相应的试验与数值计算,同时还研究了正弯曲叶片降低损失的机理.

1 试验模型及计算网格

试验级通流部分的简图示于图1.空气透平级性能试验的试验级为实物级的全模化,模化比为0.425 6,该级静叶为正弯静叶或直叶片静叶,动叶为弯扭叶片.正弯静叶级和直叶片静叶级的级压比分别为0.916 6和0.857.在试验工况下,正弯静叶级和直叶片静叶级的马赫数分别为0.355和0.474,雷诺数分别为3.18×105和4.01×105(特征长度取静叶弦长)[5].

采用Numeca商用CFD软件进行数值计算,计算模型与实物模型一致,略去静、动叶间的腔室部分.湍流模型为S-A湍流模型,叶片流道采用HOH网格拓扑结构,并对叶顶围带汽封进行局部加密,叶片流道与主流道采用FNMN连接.以直叶片静叶级网格为例,网格总数为150万,叶片流道最小正交性为32,网格最小正交性为6.1,最小正交性的网格出现在叶顶汽封中,90%的网格正交性大于72,99%的网格长宽比小于1 000,99%的网格扩展比小于1.8,网格质量良好.

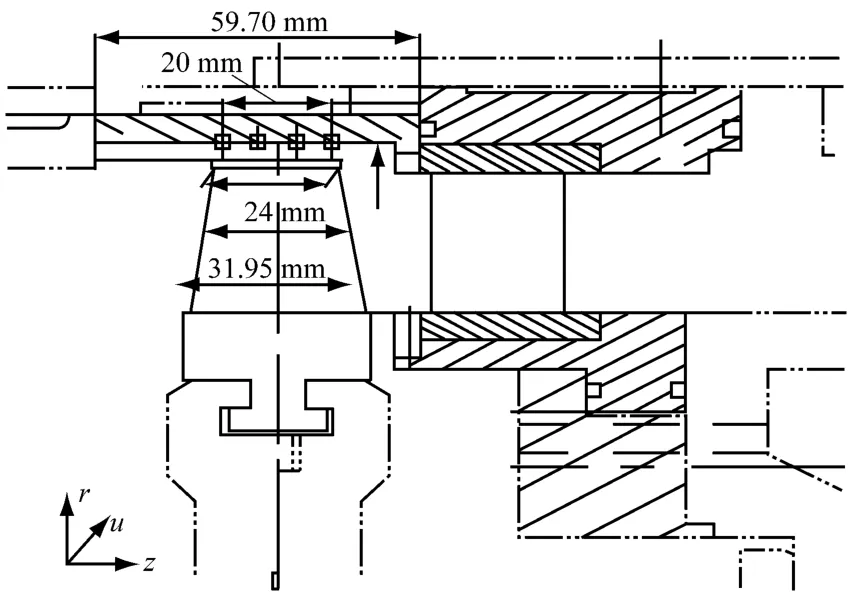
图1 试验级通流部分简图Fig.1 Sketch of flow path of the test stage

2 测量参数及试验数据的整理

单级空气透平试验台的转子为双悬臂结构,前悬臂端装有动叶轮,后悬臂端装有水力测功器的3个转动盘.前轴承(动叶轮侧)为支持轴承,后轴承(转动盘侧)为支持推力轴承.

2.1 测量参数

每个试验工况需完成下列数据的采集:

(1)测量透平级前进气管道(φ 460 mm)中的空气流量,为此需测量的参数是孔板前的温度、孔板前腔室中的压力及孔板前后腔室中的压差.

(2)测量进入透平级前空气的滞止温度.

在教学活动中突出学生自主学习能力培养，通过教师的主导来发挥学生的主体作用。开学初，学生领完教材，就开始引导同学们将教材内容粗略的进行浏览，使他们对教材内容有了初步的了解，同时也引导他们与自己的知识结构进行比较，对学习这门课有一个明确的目标，做好学习的计划，提前发现自己学习这门课可能遇到的问题，为学好本这门课提前做好心理准备。

(3)在级前和级后环形通道中,测量沿内、外壁面周向均匀分布的壁面静压.级前测孔距静叶出汽边64 mm,分别沿内、外壁面周向均匀布置6个测量点;级后测孔距动叶中心线47.5 mm,同样分别沿内、外壁面周向均匀布置6个测量点.

(4)在静、动叶间静叶出口内壁面沿1个栅距均匀布置6个测压点,测量截面距静叶出口边4.5 mm;在静、动叶间静叶出口外壁面沿1个栅距均匀布置10个测压点,测量截面距静叶出口边5 mm.

(5)测量转子的转速.

(6)测量水力测功器的功率.

(7)测量大气压.

2.2 试验数据的整理

透平级效率用轮周效率η′u和滞止轮周效率来表示,其定义式分别为:

式中 :N′u=Nw+Nx;H0=i*0-i2s;H*0=i*0-i2s-

静叶流量系数μ1和级流量系数μ的计算公式如下:

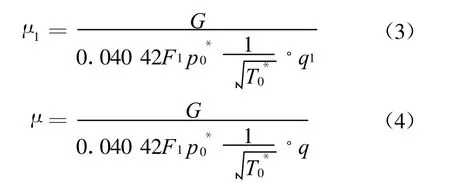
级效率与速比的关系采用4次方程拟合(速比中的圆周速度u采用根部值),在计算速比范围内,反动度和流量系数与速比的关系近似呈直线关系,本文采用直线方程进行拟合.为方便对比,对计算结果采用的处理方法与试验一样[6-7].

3 结果与分析

3.1 级效率随速比的变化

图2给出了透平级轮周效率和滞止轮周效率随速比的变化.图3给出了透平级轮周效率随速比变化的计算和试验结果的比较.由图2和图3可以看出:正弯静叶级空气透平试验的最佳速比约为0.54,最佳轮周效率为0.895 4,在最佳速比附近级效率曲线变化平缓;正弯静叶级的计算最佳速比约为0.51,最佳轮周效率为0.890 5;在低速比时,正弯静叶级轮周效率的试验曲线和计算曲线吻合较好,在较高速比时两者存在一定的差别.直叶片静叶级空气透平试验的最佳速比约为 0.55,最佳轮周效率为0.876 3;直叶片静叶级的计算最佳速比约为0.525,最佳轮周效率为0.870 0.直叶片静叶级轮周效率随速比的变化呈现出与正弯静叶级相似的规律.试验和计算结果均表明,在速比相同的条件下,直叶片静叶级的轮周效率比正弯静叶级的约低2%.

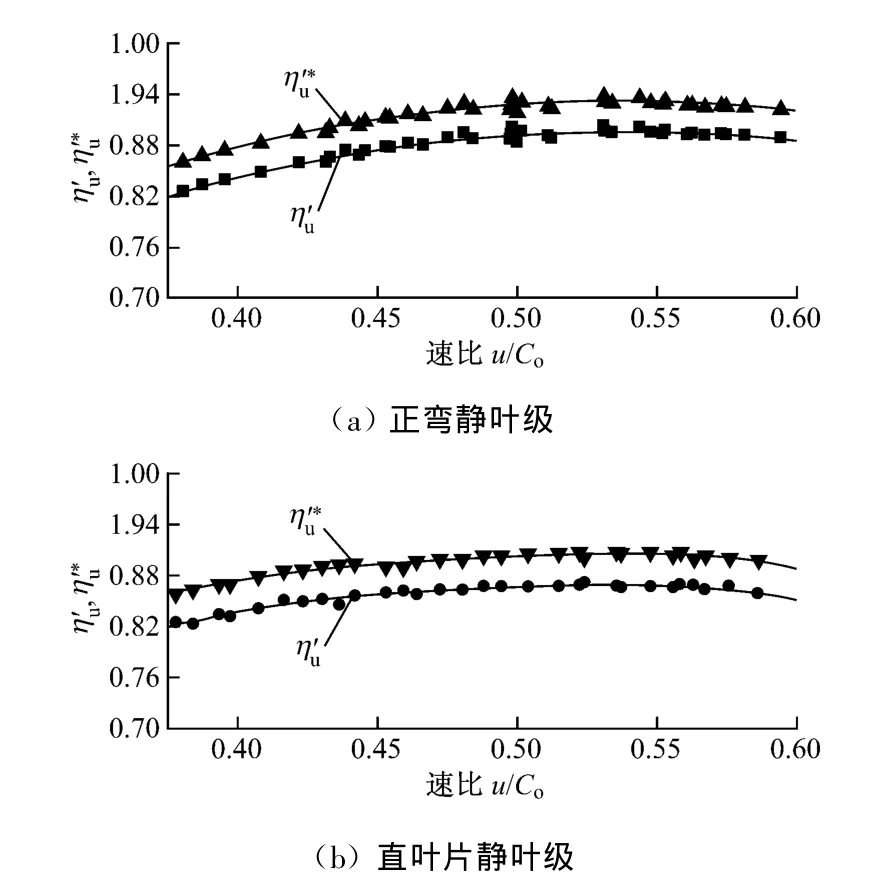
图2 正弯静叶级与直叶片静叶级轮周效率和滞止轮周效率随速比的变化Fig.2 Wheel efficiency and stagnated wheel efficiency vs.speed ratio for two turbine stages

图3 正弯静叶级与直叶片静叶级轮周效率随速比变化的计算和试验结果Fig.3 Calculation and test results of wheel efficiency vs.speed ratio for two turbine stages

3.2 反动度随速比的变化

图4给出了正弯静叶级与直叶片静叶级反动度随速比变化的计算和试验结果.从图4可以看出,计算值与试验值吻合较好.在试验和计算速比范围内,正弯静叶级与直叶片静叶级的反动度随速比的增大近似呈线性变化,当速比为0.5时,正弯静叶级根部和顶部反动度的计算值分别为0.090 0和0.341 9,直叶片静叶级根部和顶部反动度的计算值分别为0.070 6和0.318 4,可见直叶片静叶级根部和顶部反动度的计算值比正弯静叶级低0.02左右.

3.3 流量系数随速比的变化

图5给出了正弯静叶级和直叶片静叶级流量系数随速比变化的计算及试验结果.从图5可以看出,正弯静叶级和直叶片静叶级的静叶流量系数随速比的增大近似为一常数,级流量系数随速比的提高而减小.直叶片静叶级静叶流量系数和级流量系数的计算结果均大于正弯静叶级.流量系数的计算值比试验值大5%左右,主要原因可能是:①实际气流的出气角存在差异;②计算模型中没有考虑叶片型面与壁面交界处的圆角对实际通流面积的削弱因素,后一因素在模化缩小的透平级中更突出.

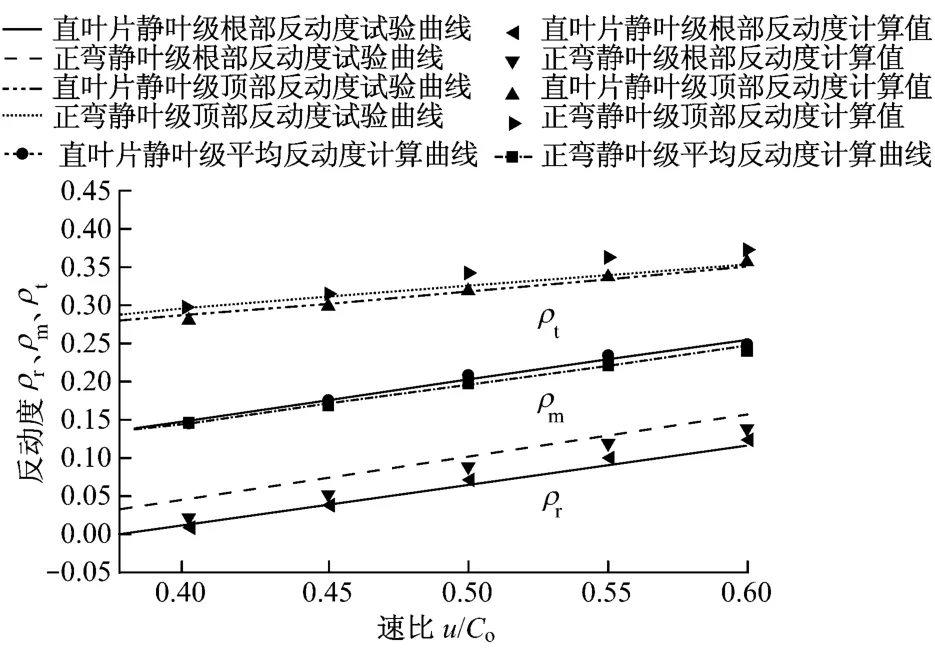
图4 正弯静叶级与直叶片静叶级反动度随速比变化的计算和试验结果Fig.4 Calculation and test results of reaction vs.speed ratio for two turbine stages

图5 正弯静叶级与直叶片静叶级流量系数随速比变化的计算和试验结果Fig.5 Calculation and test results of stage discharge coefficient vs.speed ratio for two turbine stages

3.4 级能量损失分析

在轮周效率的计算中,扣除了静叶损失、动叶损失、叶顶漏气损失和排气损失4个部分,在速比为0.5时,正弯静叶级和直叶片静叶级能量损失的计算结果见表1.从表1中数据可以看出,在速比为0.5时,直叶片静叶级轮周效率的计算结果和试验结果分别比正弯静叶级低2.6%和2.42%,2个级的轮周效率无论是绝对值还是相对变化量,其试验与计算结果均基本一致.从能量损失计算结果来看,造成正弯静叶级级效率比直叶片静叶级提高的主要原因是正弯静叶级的静叶损失和动叶损失均比直叶片静叶级小,而排气损失和叶顶漏气损失变化较小.忽略排气损失和叶顶漏气损失的变化,在正弯静叶级轮周效率的增量中,由于静叶级能量损失系数下降使轮周效率提高的量占55%,由于动叶级能量损失系数下降使轮周效率提高的量占45%.

图6给出了正弯静叶级与直叶片静叶级静叶能量损失系数沿叶高分布的计算和试验结果.由图6可以看出,直叶片静叶在根部和顶部均存在较大的端损区,而正弯曲叶片由于叶片弯曲在根部和顶部的作用,其端损区及端损均减小.叶片中部型损的试验值明显低于计算值,致使静叶能量损失系数的试验值低于计算值约1%(表1).

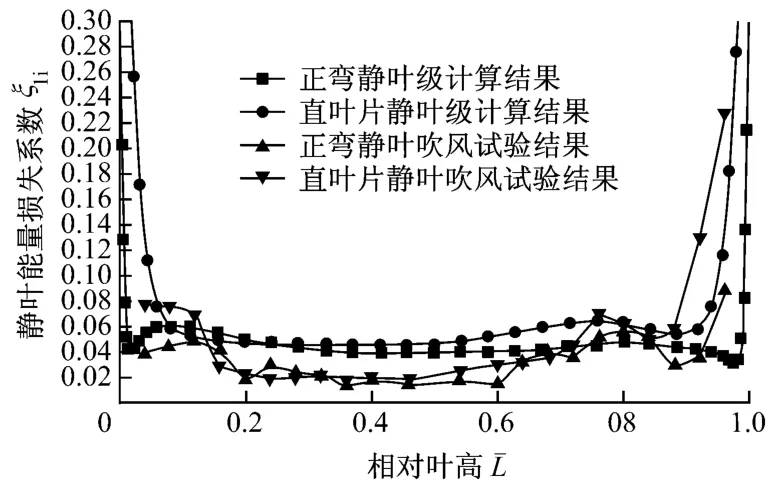
图6 正弯静叶级与直叶片静叶级静叶能量损失系数沿叶高分布的计算和试验结果Fig.6 Calculation and test results of stator energy loss coefficient vs.blade height for two turbine stages

图7给出了正弯静叶级与直叶片静叶级动叶能量损失系数沿叶高分布的计算结果.从图7可以看出,虽然2个级的动叶一样,但由于直叶片静叶两端较大的端损区对动叶的影响,使得直叶片静叶级的动叶在叶片两端有较大的端损区,造成动叶整体损失增加.

图7 正弯静叶级与直叶片静叶级的动叶能量损失系数沿叶高的分布Fig.7 Calculation and test results of rotor energy loss coefficient vs.blade height for two turbine stages

图8 正弯静叶级与直叶片静叶级ZU平面动叶进气角沿叶高的分布Fig.8 Rotor inlet angle projecting on ZU plane vs.blade height for two turbine stages

图8给出了正弯静叶级与直叶片静叶级ZU平面动叶进气角沿叶高分布的计算结果.从图8可以看出,直叶片静叶级在根部和顶部的动叶进气角均小于正弯静叶级,在中部略大于正弯静叶级,但变化一般在3°以下,仅在根部极小区域达到5°.由于2个级的试验采用同一动叶轮,进气角的变化会造成动叶损失的变化,但对照图7的损失曲线可知,进气角的变化不是动叶损失变化的主导因素.

4 结 论

(1)与采用相同叶型的直叶片静叶级相比,正弯静叶级可改善端壁的二次流流动,使静叶和动叶损失均有较大减小,速比为0.5时的试验和计算结果表明:正弯静叶级的级效率提高约2.4%～2.6%.级效率的提高是通过静叶损失与动叶损失的下降获得的,静叶约占55%,动叶约占45%.

(2)由于正弯静叶叶片力在根部使气流向下压、在顶部使气流向上压的作用,正弯静叶级根部和顶部的反动度均比直叶片静叶级大0.02左右.直叶片静叶级的流量系数略大于正弯静叶级.

[1]蔡颐年.蒸汽轮机[M].西安:西安交通大学出版社,1988.

[2]张兆鹤,崔琦,梁安江.有关叶栅损失的探讨[J].上海汽轮机,2002(1):54-61.

[3]王仲奇.透平机械原理[M].北京:机械工业出版社,1979.

[4]陈海生.弯曲叶片透平叶栅和单级轴流风机气动特性的实验和数值模拟研究[D].北京:中国科学院研究生院,2002.

[5]梁安江.静叶斜置对叶栅性能及级特性影响的研究[D].上海:上海发电设备成套设计研究所,2002.

[6]刘网扣.正弯静叶透平级静、动叶间吸漏气对级气动性能影响的试验和计算分析[D].上海:上海发电设备成套设计研究院,2009.

[7]冯师颜.误差理论与实践数据处理[M].北京:科学出版社,1996.