循环流化床锅炉汽温自抗扰控制器的优化设计

王子杰, 黄 宇, 韩 璞, 王东风

(华北电力大学控制科学与工程学院,保定071003)

循环流化床锅炉汽温具有时变、大滞后和大惯性的特点,而且由于循环流化床锅炉结构上的特点,使得给水流量的变化对汽温影响较大,这一点与煤粉炉不同,通常的串级PID常规控制方法几乎无能为力[1].因此,针对循环流化床锅炉汽温的动态特性,笔者将自抗扰控制(ADRC)引入循环流化床锅炉汽温控制系统中.但是,由于ADRC需要整定的参数较多,没有统一的整定方法,整定的过程和效果在很大程度上依赖于经验,且整定的过程耗时而繁琐,因此,参数整定问题已成为目前ADRC研究的焦点之一.张文革将时间尺度技术应用到自抗扰控制器的参数整定中,已取得了一定的成果[2].Zhiqing Gao从频域角度分析并推导出线性自抗扰控制器的参数确定方法[3].由于自抗扰控制器中存在非线性因素,虽然这些非线性因素有利于系统的调节,但也使得自抗扰控制器的参数调整不如PID参数调整直观.

在优化理论方面,量子遗传算法[4-6](quantum genetic algorithm,QGA)是一种相对新颖的优化算法,它基于量子计算原理的概率优化方法,以量子计算的一些概念和理论为基础,用量子位编码来表示染色体,用量子门作用和量子门更新来完成进化搜索,具有种群规模小、收敛速度快等特点.但QGA的旋转角查找计算复杂度较高,对于多参数复杂函数优化容易早熟收敛.为此,本文提出了基于混沌变异算子的小生境量子遗传算法,可有效克服QGA的缺点,通过几个典型函数的测试,结果表明了本算法的有效性;同时,把该算法应用于自抗扰控制器主要参数的寻优,并对其进行了仿真,仿真结果表明：优化后的自抗扰控制具有良好的控制效果,该算法应用于循环流化床锅炉汽温系统的控制可行有效.

1 自抗扰控制原理

1.1 自抗扰控制器的基本结构

自抗扰控制器的结构示于图1,它由3个相对独立的部分构成：①跟踪微分器TD,其作用是安排过渡过程,并给出此过程的微分信号;②扩张状态观测器ESO,其作用是跟踪对象输出y,并估计对象的各阶状态变量和对象总扰动实时作用量;③非线性控制器NLSEF,它利用非线性状态误差反馈对被控对象进行控制.

图1 自抗扰控制器结构图Fig.1 The structu re sketch of active-disturbancerejection controller

1.2 自抗扰控制器的离散算法实现

以典型二阶对象为例,给出步长为h的欧拉法离散形式算法.假设对象为：

式中：w(t)为未知扰动;f(x,x◦,w(t))为未知函数,表示对象扰动的总和作用量;u(t)为控制输入;b为控制输入的系数,假设已知;x为系统的状态变量;y为系统输出.

1.2.1 TD的离散算法实现

离散TD的实现方程如下：

式中：v0(k)为参考输入信号;v1(k),v2(k)分别为离散TD的2个输出;h为步长;h0为滤波因子,一般取为3 h～10 h;r是TD的参数,其大小可以根据过渡过程快慢的需要和系统的承受能力来选择.

fhan(v1(k)-v0(k),v2(k),r,h0)的表达式如下：令x1=v1(k)-v0(k),x2=v2(k),则

式中：sign为符号函数.

适当选择跟踪微分器的参数r,就可以对参考输入v0(k)安排出期望的过渡过程v1(k)和该过渡过程的微分信号v2(k).

1.2.2 ESO的离散算法实现

离散ESO的实现方程如下：

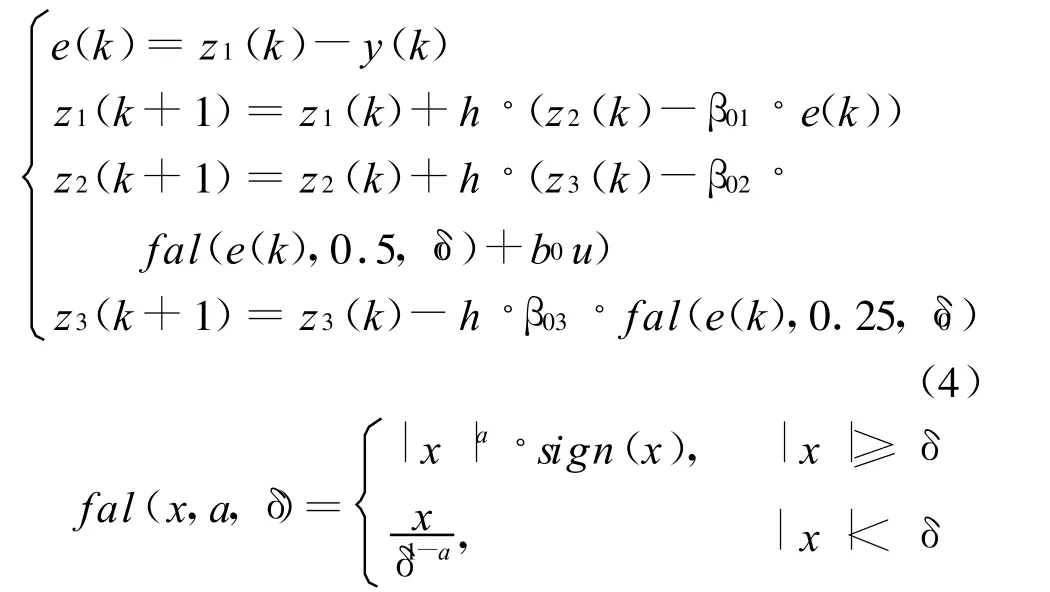
式中 ：z1 、z2 、z3 为 ESO 的状态变量 ;β01 、β02 、β03为可调参数,决定了ESO的估计能力;b0为补偿因子;δ0为可调参数,其大小可以取仿真步长h[7].

其中z1、z2能够很好地跟踪对象输出y及对象输出的变化率,z3用于估计出对象扰动的总和作用量 f(x(t),(t),w(t)),并反馈到控制量u(t).

1.2.3 NLSEF的离散算法实现

离散NLSEF的实现方程如下：

式中 ：一般取 α1=0.75,α2=0.5;b1,b2是控制器的参数.

其中只有b0、b1、b2 3个参数需要进行调整[7],而这3个参数与PID控制器的3个参数有很多相似之处,但是自抗扰控制器存在非线性环节,参数调整不如PID简单直观.为此,引入优化理论,对ADRC的控制参数b0、b1、b2进行优化整定,以搜索出控制器参数的最优值.

2 基于混沌变异算子的小生境量子遗传算法

2.1 量子遗传算法

量子遗传算法是一种新的遗传算法,在量子进化策略中,使用一种基于量子比特的编码方式.它最本质的特征就是充分利用了量子态的叠加和相干性,以及量子比特之间的纠缠态.在量子遗传算法中,一个量子位的状态可表示为：

式中：|0〉表示状态0,|1〉表示状态 1;α和β可以是复数,表示相应状态的概率幅,且满足下列归一化条件：

式中 ：|α|2表示|0〉的概率 ;|β|2表示|1〉的概率.

可以看出,如果有一个具有m个量子比特位的系统,那么它能同时表示出2m个状态.其描述为：

式中 ：|αi|2+|βi|2=1,i=1,2,…,m.

在变异中加入最优个体的信息来引导进化,从而加快算法的收敛,称为量子旋转门.

量子旋转门的调整操作如下：

式中：[αi βi]T为染色体中的第i个量子位;θi为旋转变异角,其大小和方向的调整策略见文献[5].

2.2 小生境进化策略

小生境技术是遗传算法中避免局部收敛和早熟、维持种群多样性的一种有效方法.小生境技术的思想是通过控制子种群之间的排挤和竞争,使各个子种群在进化中动态形成各自独立的搜索空间,从而实现对多个局部极值进行同步搜索.算法中的小生境半径定义了各个子种群独立的搜索空间,一旦某个小生境最优个体进入了其他小生境的搜索空间,则重置该个体,并在其所在的小生境内重新选择最优个体,从而使每个小生境子种群自然形成,降低了量子遗传算法陷入局部最优的概率.

2.3 混沌变异

混沌是自然界广泛存在的一种非线性现象,具有随机性、遍历性、初始条件敏感性等特点,已被广泛应用于随机优化.在寻优的过程中,对每个小生境的种群最优个体进行混沌迭代变异,变异空间随着代数的增加而逐渐减小.在进化初期,变异尺度大,有利于算法在广阔的空间搜索全局最优解;在进化后期,变异尺度小,在小空间内紧紧围扰局部极点精细搜索,有利于提高解的精度.本文使用的混沌映射迭代方程为：

式中：0＜y(1)＜1且y(1)≠1

2.4 基于混沌变异算子的小生境量子遗传算法

结合小生境策略全局优化与变尺度混沌变异精细搜索的优点,提出一种全新的量子遗传算法,具体流程如下：

(1)初始化小生境粒子种群.

(2)用适应度函数对种群中所有个体进行适应值评价,在每个子种群内部进行最优个体迁移保存.

(3)保留最优个体以及与之对应的旋转角度,判断是否满足终止条件.若满足,则算法终止,符合全局最优条件的保留为全局最优,否则执行下一步.

(4)对所有小生境子种群的最优个体实行混沌变异,进一步提高搜索的精度,然后再回到步骤(2),直到循环结束.

2.5 算法性能测试

为了检验本文提出算法的性能,将该算法应用到实数搜索空间的数值函数最优化领域中.利用如下几个函数进行测试：

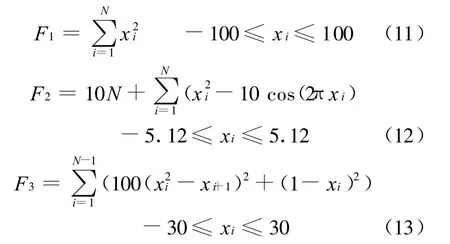
以上3个测试函数中 N=30,最大迭代次数G max=1 000,种群规模M=80,种群数量Niche=10.表1给出了50次运行的平均结果.

从表1中可以看出,本文提出的基于混沌变异算子的小生境量子遗传算法的计算精度明显优于遗传算法和标准量子遗传算法.

3 循环流化床汽温自抗扰优化控制

3.1 循环流化床燃烧系统的数学模型

根据文献[8-9],某国产循环流化床锅炉主汽温的传递函数如下：

式中：W1(s)为惰性区传递函数;W 2(s)为导前区传递函数;W H(s)为在给水流量扰动对主汽温的传递函数.

上式中对应锅炉负荷在25%～100%变化时,K1为0.8～0.5,T1为100～80 s;K 2为2～1,T2为50～35 s;K H为0.3～0.2,T H为 180～150 s.随负荷的增加,汽温对象的增益和时间常数均逐渐减小,而且表现出明显的大惯性和纯滞后特性,属于明显的难控制对象.

3.2 优化目标函数

根据热工过程控制系统设计中常用的性能指标,采用如下形式的目标函数：

同时,为了减少系统出现稳态误差,当运行时间t＞T时(T为调节时间估计最大值),其目标函数：

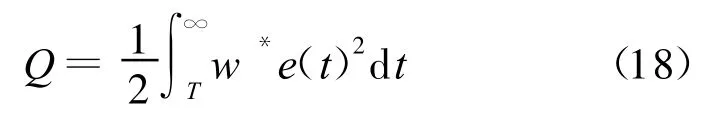
式中：w取一较大数值,在本文中选取w=1 000;T=2 000 s.

3.3 控制器参数整定结果及性能分析

由于控制方案采用串级控制方案,内回路仍然采用PID控制,其控制参数采用本文提出的基于混沌变异算子的小生境量子遗传算法进行寻优,寻优算法的基本参数见2.5节.

在100%负荷下,内回路PID优化结果为：k p=39.980 4;ki=0.082 3;kd=189.833 8.

利用本算法对自抗扰控制器参数进行寻优,算法迭代过程示于图2,其中Best J为目标函数值,最优Best J=233.558.

图2 迭代过程Fig.2 Iteration process

寻优得出的自抗扰控制器的最优参数为：b0=0.000 193;b1=0.058 98;b2=22.739 41.其在给定值作单位阶跃响应下的仿真结果示于图3(实线),调节时间为674 s(±5%),上升时间为425 s,超调量为9.08%.

同时,为了与PID控制器的性能进行比较,在图3中也给出了最优PID控制器的控制效果(图中虚线所示).对应外回路PID参数也是通过本文提出的优化方法得出的,其参数为：k p=2.629 5;k i=0.006 2;kd=191.202 3,PID控制器调节时间为1 094 s(±5%),上升时间为 469 s,超调量为9.56%.从图3可以看出,在给定值扰动下,自抗扰控制器的控制品质略优于最优PID控制器.

图3 100%负荷对象仿真曲线Fig.3 Sim ulation cu rve of the object under 100%load

由于过热汽温对象的惯性时间常数会受到负荷等其他因素的影响而产生很大改变,或者由于某种原因使得对象的增益发生变化,因此假定对象惰性区模型变化后分别为：

控制系统的其他环节保持不变,得到在设定值扰动下的响应曲线(图4).

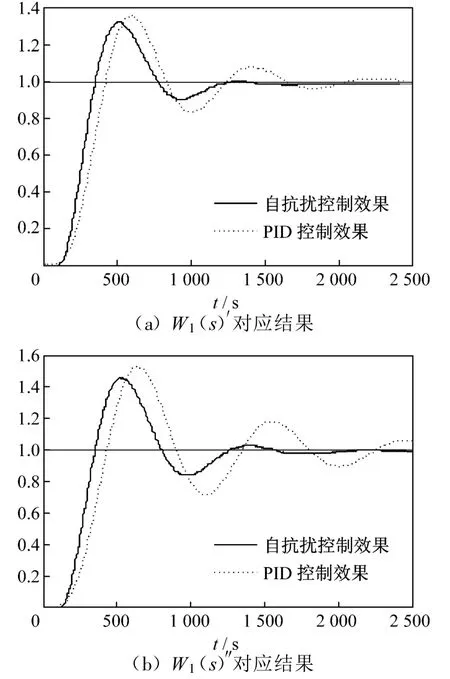
图4 对象模型发生变化时系统的响应输出曲线Fig.4 Output curves of system response when the object model is changed

从图4可以看出,通过本算法整定结果选出的最佳整定参数,在对象特性发生变化的情况下,仍能获得比最优PID控制器更好的控制效果,说明该算法具有较强的鲁棒性和较好的调节品质.

由于在循环流化床锅炉中,给水流量对汽温的影响较大,在100%负荷时,对给水作单位阶跃扰动,系统的响应曲线示于图5.

图5 扰动作用下系统的响应输出曲线Fig.5 Output curves of system response under disturbance

从图5可以看出,自抗扰控制器对扰动具有良好的抑制作用,效果明显优于最优PID控制器的控制效果.

4 结 论

本文所提出的基于混沌变异算子的小生境量子遗传算法,可有效克服量子遗传算法容易陷入局部极小的缺点,提高了量子遗传算法的计算精度.在此基础上,利用提出的算法对自抗扰控制器参数进行寻优,获得了在某典型工况下的最优自抗扰控制器参数.仿真结果表明：利用该算法得出的控制系统比最优PID控制系统的控制效果更好;同时,在对象特性发生变化以及给水流量发生变化的情况下,自抗扰控制器都能够获得较好的控制效果,具有较强的鲁棒性.

[1] 牛培峰.循环流化床锅炉汽温自适应解耦控制系统[J].自动化学报,1999,25(1)：127-132.

[2] 张文革.时间尺度与自抗扰控制器[D].北京：中科院系统科学研究所,1999.

[3] GAO Z Q.Scaling and band wid th-parameterization based controller tuning[C]//Proceedings of the 2003 American Control Conference.Denver,USA：[s.n.],2003：4989-4996.

[4] NARAYANAN A,MOORE M.Quantum-inspired genetic algorithms[C]//Proceedings of IEEE Internationa l Conference on Evolutionary Computation.Piscataw ay,USA：[s.n.],1996：41-46.

[5] 焦嵩鸣,韩璞,黄宇,等.模糊量子遗传算法及其在热工过程模型辨识中的应用[J].中国电机工程学报,2007,27(5)：87-92.

[6] 王凌,吴昊,唐芳,等.混合量子遗传算法及其性能分析[J].控制与决策,2005,20(2)：156-158.

[7] 韩京清.自抗扰控制技术[J].前沿科学,2007,1(1)：24-31.

[8] 王东风.循环流化床锅炉汽温系统的多模型自适应预测控制[J].自动化仪表,2003,24(7)：46-49.

[9] 刘吉臻,岳俊红,刘向杰,等.循环流化床锅炉主汽温的模糊预测函数控制[J].动力工程,2007,27(4)：537-540.