基于Ansys电磁轨道炮临界速度分析

高 博 张建革 李 涌

（1.郑州机电工程研究所，郑州 450015；2.海军驻郑州地区军事代表室，郑州 450015

1 引言

电磁轨道炮是由在两条平行联接着大电流源的固定导轨和一个与导轨保持良好电接触、能够沿着导轨轴线方向滑动的电枢组成，如图1所示。当接通电源时，电流沿着一条导轨流经电枢，再由另一条导轨流回，从而构成闭合回路。当强大的电流流经两平行导轨时，在两导轨之间产生强大的磁场，这个磁场与流经电枢的电流相互作用，产生强大的电磁力，该力推动电枢和置于电枢前面的弹丸沿着导轨加速运动，从而获得高速度。电枢在轨道上运动过程中，导轨将承受移动动载荷（电磁扩张力）的作用。当电枢到达某一固定速度，即临界速度时，有可能产生产生瞬时高应力和高应变，加剧导轨的烧蚀。

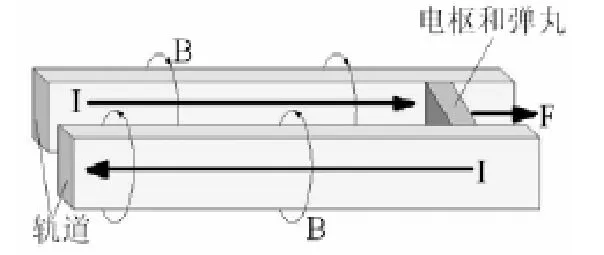
图1 电磁轨道炮原理图

2 轨道炮系统的简化建模

电磁轨道炮的通用结构形式如图2所示。

图2 轨道炮通用结构形式

在这里，轨道主要起传导电流的作用；封装主要用来维持轨道炮的炮口形状，以抵消电磁扩张力的扩张作用；支撑材料和绝缘体将轨道和外部封装隔离开来，并加固整体结构。弹丸在导轨上运动时，导轨将会承受不均匀的电磁压力，并且该电磁压力随着电枢的运动而向炮口移动，直至弹丸离开炮口。因此，该过程可以将轨道炮模型简化为图3所示。该模型将导轨简化为一固定在弹性支撑上的梁，导轨下面的支撑材料和封装简化为一系列间断的弹簧，并固定在地面上。因此轨道简化模型的动力学方程

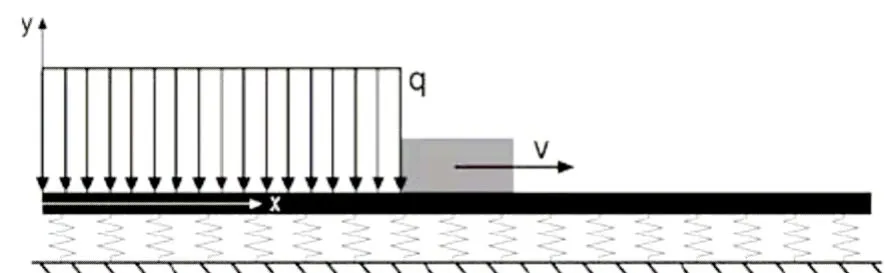
图3 轨道炮动力学模型

载荷函数 q[ 1−H(x−Vt)]在上述方程中表示以恒定速度 V沿着轨道向前移动的电磁压力，以海维塞得阶跃函数表示。电磁压力q也假设为恒定，因此

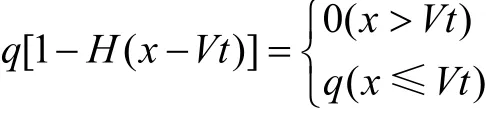
用数值方法求解方程（1），可求得临界速度

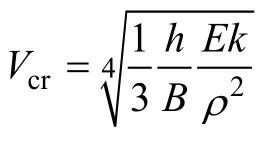
其中h和B分别为轨道厚度和高度，E和ρ分别为轨道弹性模量和密度，k为支撑材料的弹性系数。

3 ansys中仿真计算结果

本例中假设轨道长2.75m，轨道为铜导轨，建模时用101个节点即100个单元表示轨道梁，每个节点下面安装一个弹簧，图4为ansys中的结构模型。

图4 轨道炮仿真模型

根据试验参数，求得Vcr=1145m/s；用ansys进行仿真时其他条件不变，仅改变载荷的移动速度V，按 V=450m/s，V=800m/s，V=Vcr=1145m/s，V=1600m/s分别进行仿真，以中间节点（节点51）作为比较对象，分析各种不同速度下该节点的纵向最大位移值。仿真结果如图5～8所示。

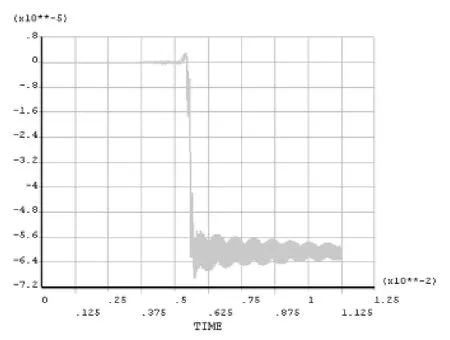
图5 V=450m/s

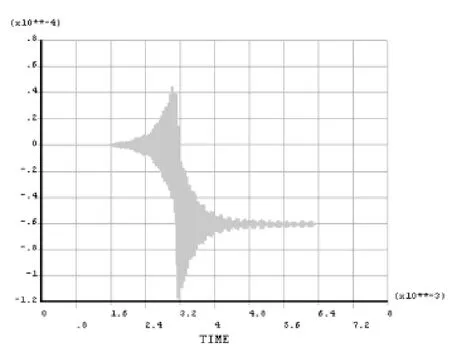
图6 V=800m/s

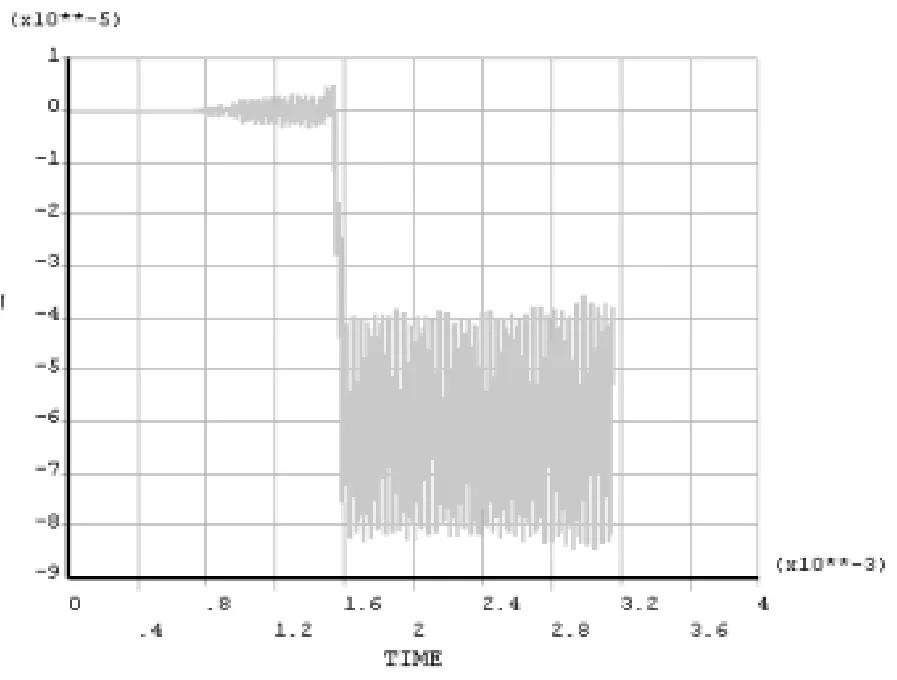
图7 V=Vcr=1145m/s

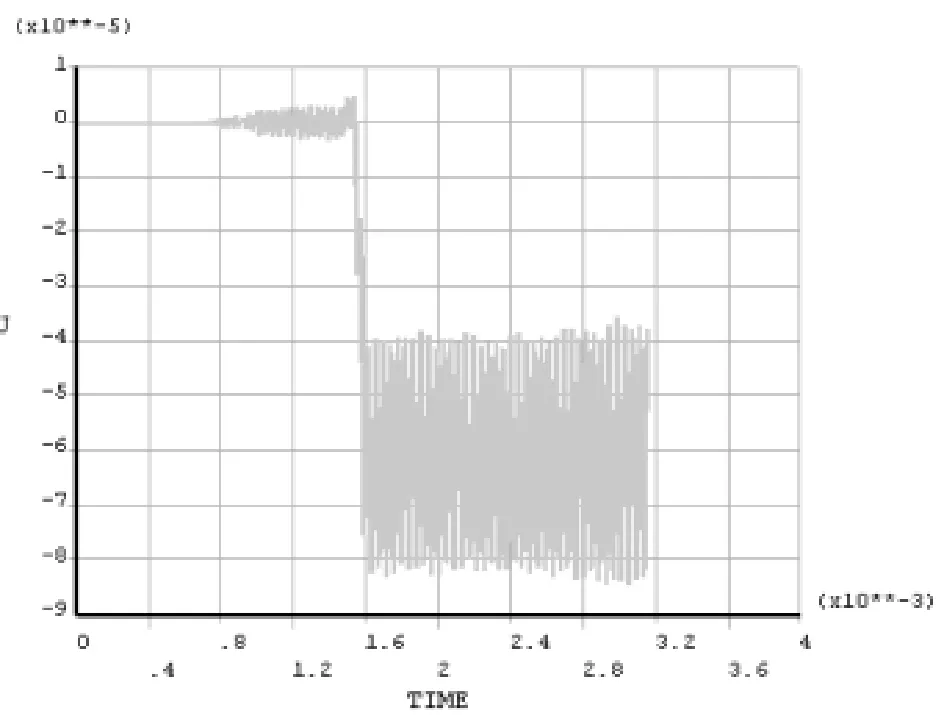
图8 V=1600m/s

另外，我们比较了不同的支撑材料弹性系数值对轨道炮导轨应变值的影响，如图9～11所示，3张图分别表示弹性系数kf=4.15e9，kf=5.15e9，kf=6.15e9时，电枢载荷分别以临界速度运行时，轨道的纵向应变图。

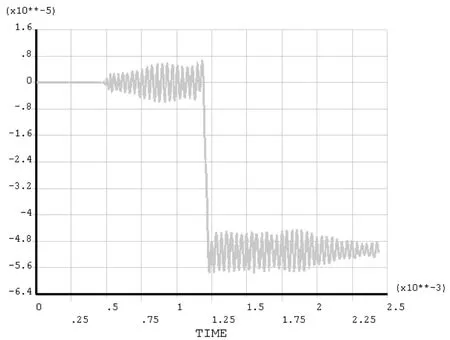
图9

图10

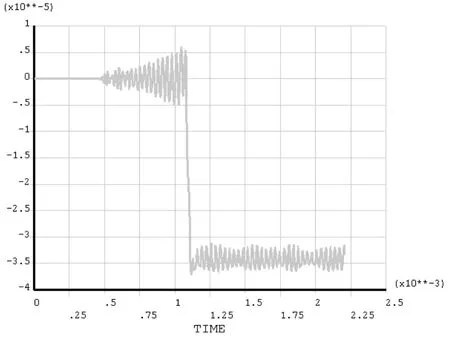
图11

4 结果分析

由仿真结果可知：

（1）不同载荷速度下节点51的纵向最大位移值见表1。

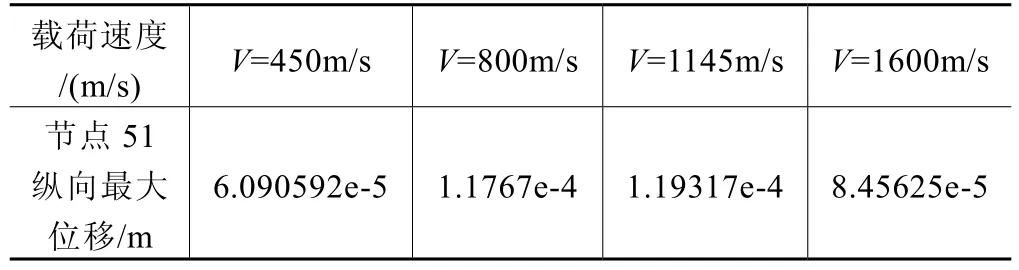
表1

（2）不同弹性系数下，载荷以临界速度运行时，节点51的纵向最大位移值见表2。

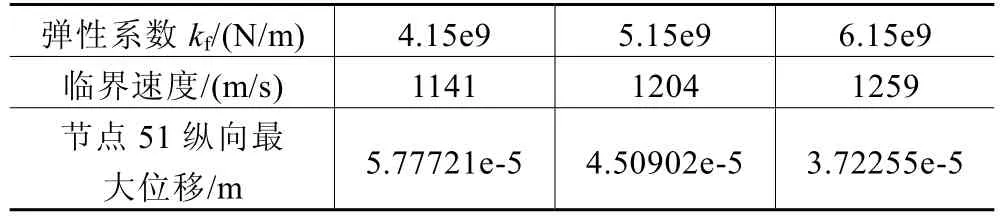
表2

通过上述两组数据，我们可以的出以下结论：

（1）当电枢速度V=Vcr时，导轨的纵向应变最大，即此时导轨的烧蚀最严重，当电枢速度大于或小于临界速度时，导轨的纵向应变均小于临界速度时对应的应变值，因此仿真结果可以充分证明电磁轨道炮发射过程中临界速度的存在以及理论简化建模的准确性。

（2）设计过程中，支撑材料的弹性系数对轨道的纵向应变影响比较大，并且随着弹性系数的增大，轨道的纵向应变值呈现明显减小的趋势，这对于减轻轨道的烧蚀至关重要。

因此，我们在对轨道炮进行设计过程中一方面要充分考虑临界速度对轨道应变的影响，

设计时要尽可能地通过优化轨道炮系统中的各个参数，提高轨道炮的临界速度，至少要使轨道炮的临界速度大于所预定的炮口速度，从而减少对导轨的烧蚀影响；另一方面在提高临界速度的过程中也要找到主要的影响因子，通过仿真可以看出，支撑材料的弹性系数便是其中之一，设计时要在条件允许的情况下尽可能地提高支撑材料的弹性系数，从而以最快的方式提高轨道炮的临界速度，从而得到合理的结构形式。

[1]倪栋,段进,徐久成等.通用有限元分析ANSYS7.0. 北京∶电子工业出版社,2003.10.

[2]王莹,肖峰.电炮原理.北京∶国防工业出版社,1995.

[3]Jerome T. Tzeng. Dynamic Response of Electromagnetic Railgun Due to Projectile Movement[J].IEEE Transaction on Magnetics, Vol. 39, No. 1, 472-475, 2003.