基于灰色系统模型的国库现金流预测*

□ 牛润盛 刘 琼

(1、中国人民银行广东汕尾市中心支行，广东 汕尾 516600;2、广东汕尾市职业技术学院，广东 汕尾 516600)

我国学者郑聚龙教授于1982年创立了灰色系统理论，经过20多年的发展，已形成以系统分析、信息处理、建模预测、决策控制为主要内容的系统体系，广泛应用于工程控制、经济管理、社会系统等众多领域。其中的灰色动态预测模型自提出以来在我国的许多行业得到了广泛应用，本文将运用灰色系统模型对国库现金进行预测。

一 灰色系统模型概念及DPS数据处理系统

灰色系统模型通过将波动性较大的离散的随机原始序列作累加生成，得到指数规律性较强的累加生成序列，再经序列建模的参数估计后，将计算结果逆向累减得到原始序列预测值。根据方程阶数和变量个数不同，有 GM(1，1)、GM(N，1)、GM(1，N)等类型。

灰色系统模型(Grey Model，GM)具有弱化序列随机性、波动性，挖掘系统演化规律的独特功效;另一个显著特点是所需样本数据小，仅用4个数据就可以估计出模型参数，且可达到一定的模拟精度，对大样本数据的模拟精度反而不高;使用灰色系统理论的思想、方法对原始观测数据进行必要处理，将会大大改善统计模型的拟合及预测性能。

DPS数据处理系统(Data Processing System)，采用全屏幕交互编辑方式设计，配有多级下拉式菜单，用户使用时整个屏幕犹如一张工作平台，随意调整，操作自如，故形象地称其为DPS数据处理工作平台，简称DPS平台。DPS系统集数据全屏幕编辑制表、试验设计及统计分析、多元分析、数值计算以及建立各种数学模型等多项功能为一体，广泛用于教学、科研和生产各个领域。

二 灰色系统模型的一般建模过程

灰色系统模型的一般建模过程如下:

(一)对原始序列累加处理

X(0)为原始非负序列①:

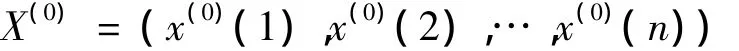
其中，x(0)(k)≥0，k=1，2，…，n;

一次累加生产序列②(即1-AGO序列)，表示为X(1):

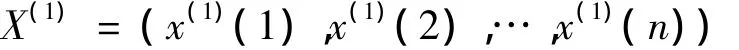
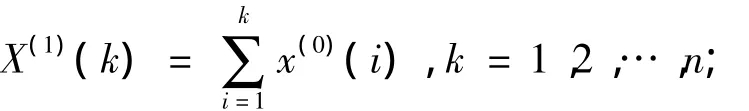
由X(1)的相邻项平均得到X(1)的紧邻均值生成序列Z(1)，表示为:

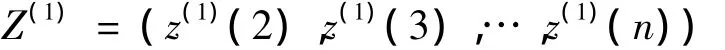
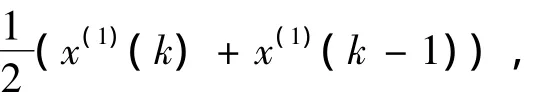
根据上述序列，有灰色系统模型GM(1，1)的基本形式:

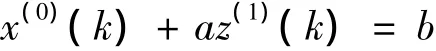
对应的白化方程形式③:

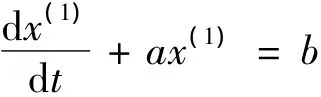
其中，a为发展系数，b为灰色作用量，都是待定参数。

(二)构造GM(1，1)模型方程组的矩阵形式，并求解参数

GM(1，1)模型的微分方程基本形式:

有方程组的矩阵形式:Y=Bα

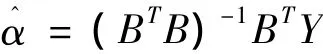
(三)求的时间响应序列，累减得到原序列的预测值

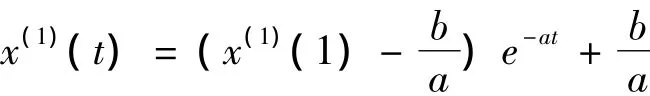
相应地，GM(1，1)模型基本形式x(0)(k)+az(1)(k)=b的时间响应序列:

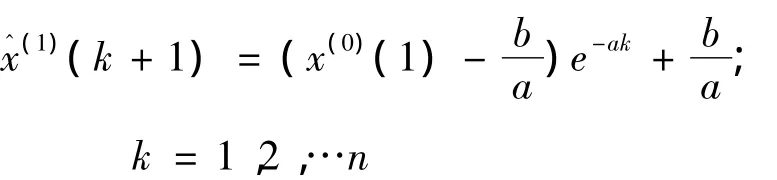
累减得还原值:

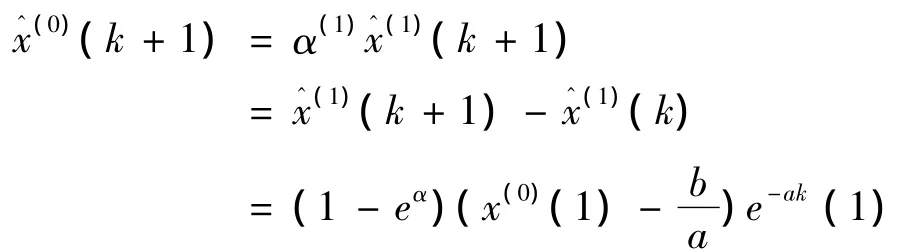
(四)模型检验

X(0)为原始序列,为相应的模拟序列，ε(0)=X(0)-为残差序列，则X(0)的均值、方差分别为:

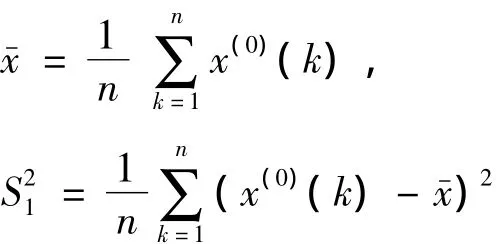
残差的均值、方差分别为:

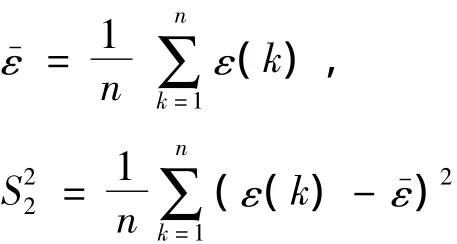
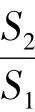
一般均方差比值C越小越好(因为C小说明S2小，S1大，即残差方差小，原始数据方差大，说明残差比较集中，摆动幅度小，原始数据比较分散，摆动幅度大，所以模拟效果好，要求S2与S1相比尽可能小)，以及小误差概率p越大越好，给定 α，ε0，C0，p0的一组取值，就确定了检验模型模拟精度的一个等级，常用的精度等级见表1。软件DPS的分析结果也提供了C、p的检验结果。

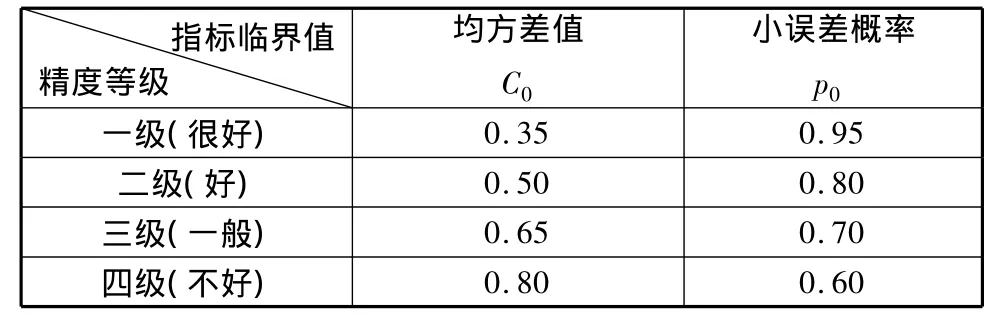
表1 精度检验等级参照表

(五)残差修正模型

当GM(1，1)模型的精度不符合要求时，可用残差序列建立GM(1，1)模型，对原来的模型进行修正，以提高精度。

原序列X(0)的残差序列表示为:ε(0)=(ε(0)(1)，ε(0)(2)，…，ε(0)(n))，如果序列中存在负数 ε(0)(i)，i=1，2，…n，为使残差序列满足灰色模型系统的要求，需对序列先进行正则化处理:

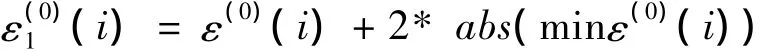
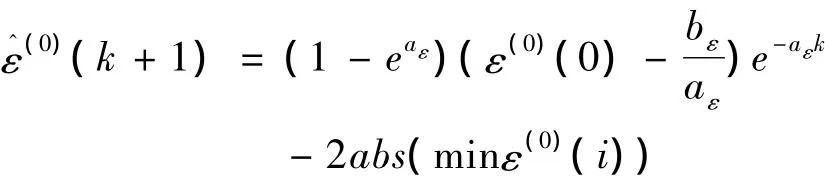
从而对原模型公式(1)修正，得到残差修正模型:

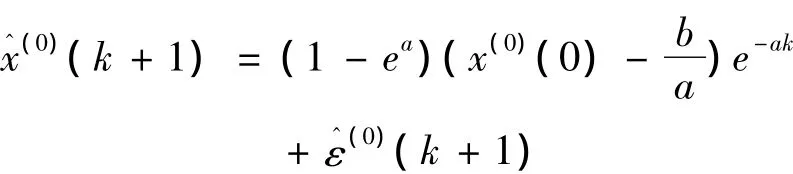
(六)建立新陈代谢GM(1，1)进行动态预测

在实际建模过程中，原始数据序列的数据不一定全部用来建模。我们在原始数据序列中取出一部分数据，就可以建立一个模型。一般说来，取不同的数据，建立的模型也不一样，即使都建立同类的GM(1，1)模型，选择不同的数据，参数a，b的值也不一样。这种变化，正是不同情况、不同条件对系统特征的影响在模型中的反映。

设原始数据数列

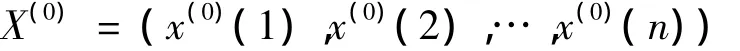
根据所用样本数据的不同，有以下4种GM(1，1)模型

1、用X(0)=(x(0)(1)，x(0)(2)，…，x(0)(n))建立的GM(1，1)模型称为全数据GM(1，1);

2、∀k0〉1，用X(0)=(x(0)(k0)，x(0)(k0+1)，…，x(0)(n))建立的GM(1，1)模型称为部分数据GM(1，1);

3、设x(0)(n+1)为最新信息，将x(0)(n+1)置入X(0)，称用X(0)=(x(0)(1)，x(0)(2)，…，x(0)(n)，x(0)(n+1))建立的模型为新信息GM(1，1);

4、置入最新信息x(0)(n+1)，去掉最老信息x(0)(1)，称用X(0)=(x(0)(2)，…，x(0)(n)，x(0)(n+1))建立的模型为新陈代谢GM(1，1)，又叫动态等维灰色系统模型。

根据经验，以预测精度为标准，新陈代谢模型相对是比较理想的模型。一般情况下，随着系统的发展，老数据的信息意义将逐步降低，在不断补充新信息的同时，及时地去掉老信息，建模序列更能反映系统在目前的特征。尤其是系统随着量变的积累，发生质的飞跃或突变时，与过去的系统相比，已是面目全非。去掉已根本不可能反映系统目前特征的老数据，显然是合理的。因此本文将建立新陈代谢GM(1，1)进行预测。

三 灰色系统模型预测的实证分析

本文选用的数据是汕尾市2008年1月-2009年12月国库库存余额月均值，共24个样本数据，使用软件是数据处理系统DPS7．054。

(一)数据与模型选取

灰色系统模型在小样本数据方面有独特优势，最少使用4个样本即可估计参数，本文将使用前4个月的数据对第5个月数据，建立GM(1，1)进行预测。具体来说，使用2008年1-4月数据建立GM(1，1)模型，对2008年5月预测，然后2008年2-5月数据建立新陈代谢GM(1，1)模型，以此类推，每次建立的新陈代谢模型的样本数据都是4个，预测期限都是1。

(二)模型检验结果及相对误差

24个月均数据共建立20个GM(1，1)模型，其模型检验参数模型检验结果及相对误差(表2)。表2中，除少数几个相对误差较大外，新陈代谢模型预测的效果还是比较好的。对比实际值和相对误差的绝对值发现(图1)，灰色模型的预测相对误差主要出现在实际值突变点。

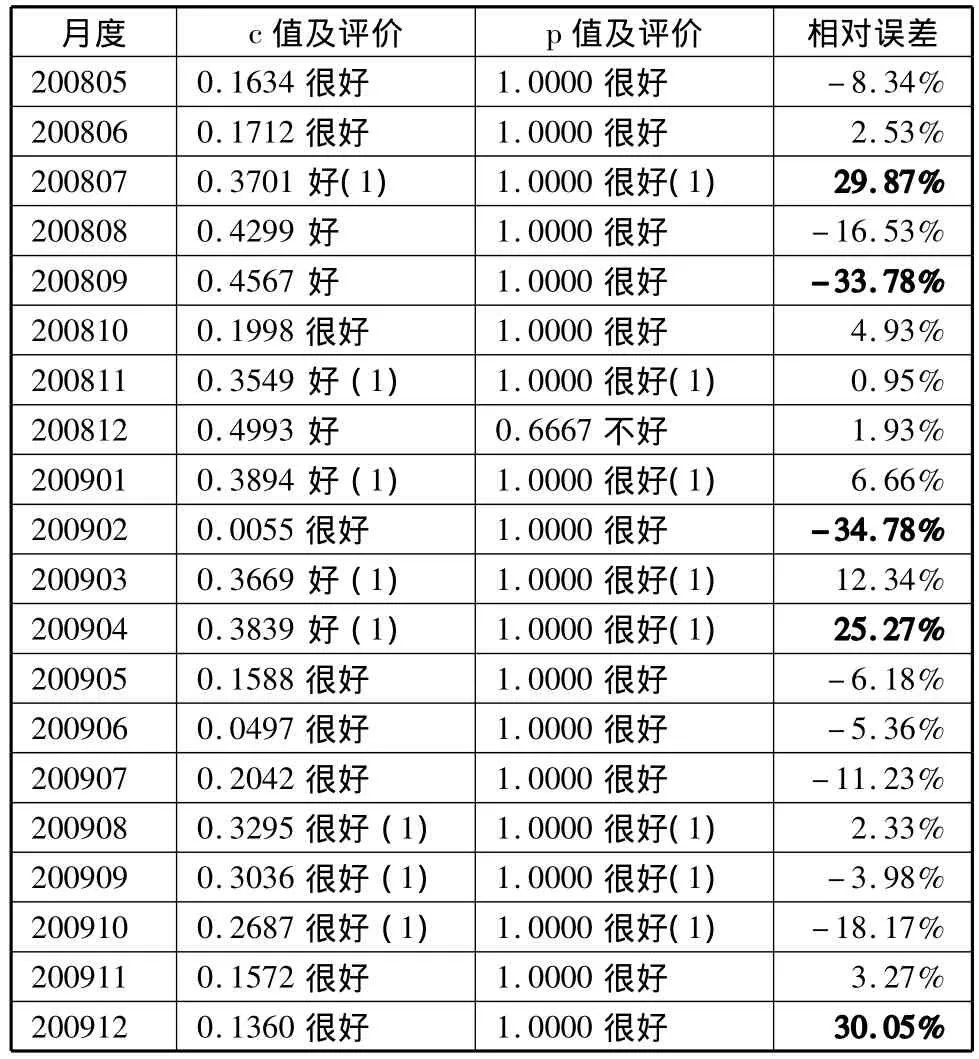
表2 GM(1，1)模型检验结果及预测精度

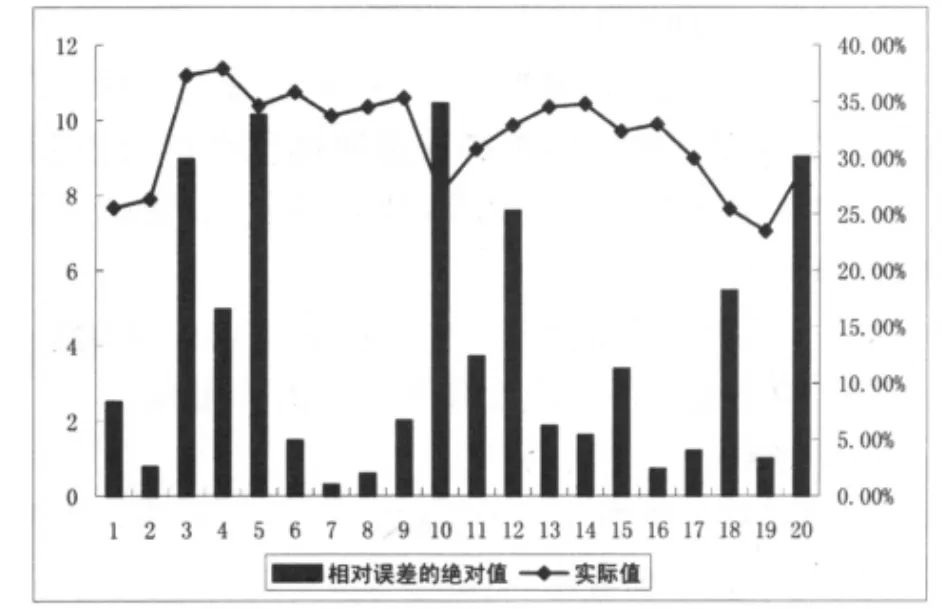
图1 实际值和相对误差的绝对值对比

四 灰色系统模型与其他预测方法的结合

本文采用的新陈代谢灰色系统模型，使用前4期的数据预测第5期，并动态更新数据进行1步预测，最大限度的利用了新信息，减少了老信息对模型的影响，但正因如此也忽略了国库现金流的季节性、周期性，从而在突变点的预测效果不理想。如果能把灰色系统模型与其他预测方法结合或许能解决这个问题。

任何一种模型只是研究对象若干侧面中某一个(或某几个)侧面，同时由于系统的发展演化过程，往往是许许多多可知因素和未知因素、确定性因素和不确定性因素相互作用的结果，仅用单一模型难以全面地揭示研究对象的发展变化规律。在众多模型中，不同模型各有其不同特点，对于揭示研究对象的某一侧面的变化规律有不同优势。灰色系统模型通过数据累加的方法，将序列波动性进行研究，但是模拟序列时仅仅使用指数方法，如果能结合线性回归、ARMA、神经网络等方法，有可能深化对系统演化规律的认识，提高预测的精度。

注释

①灰色系统模型要求原序列不含负数;方便起见，字母大写表示某一序列，对应小写表示序列的一个元素．

②一般序列经过一次累加或更高次累加表现出很好的指数特征;大写字母右上角括号内数字代表序列的累加次数，如0代表没有经过累加，1代表累加一次;代表序列每个元素的小写字母后面括号内数字代表其是元素排序，即第几个元素．

③详细内容见参考文献2《灰色系统理论及其应用》p151-167．

［1］邓聚龙．灰色理论与方法［M］．北京:石油工业出版社，1993．

［2］刘思峰，郭天榜，党耀国等．灰色系统理论及其应用［M］．北京:科学出版社:l999．