谐波级数表示与周期时变参数模型间关系

曲 强， 金 明 录

（1.大连理工大学 信息与通信工程学院，辽宁 大连 116024；2.辽宁科技大学 电子与信息工程学院，辽宁 鞍山 114051）

0 引 言

循环平稳随机过程的研究主要起始于20世纪70年代，最初的研究主要集中在循环平稳随机过程的分解上，将循环平稳随机过程分解为一组平稳随机过程的表达式，这些平稳随机过程之间是相关的.之后研究的重点又放在信号的自相关函数和功率谱上，由于信号是周期的或几乎周期的，可以用傅里叶级数来表示.随后Gradner又提出了谱相关理论和谱冗余概念，并将其应用于解决各种实际问题之中［1］.

循环平稳随机过程的分析与处理已经广泛应用于生产和生活的各个领域，越来越受到各学科对其研究的重视，并成为信号处理学界近年来感兴趣的研究热点之一［2～4］.对于循环平稳随机过程的模型已有众多研究，文献［5］研究了适用于循环平稳随机过程的线性时变周期系统的周期滤波器的设计问题，提出了采用直接型和时间基函数展开型自适应滤波器设计问题，文献［6、7］分别研究了采用周期自回归模型和向量自回归模型实现对二阶循环平稳随机过程的建模问题，文献［8］研究了线性周期时变模型与线性时不变多输入多输出结构间的等价性关系.此外，文献［9、10］将谐波级数表示应用到电磁场分析与计算之中并获得较好的效果.

谐波级数表示（HSR）和周期时变参数模型是描述循环平稳随机过程的两种常用参数化方法，本文从循环平稳随机过程的谐波级数表示出发，研究谐波级数表示与周期时变参数模型间的关系，并提出一种构造周期时变参数模型的方法，最后通过仿真验证这两种模型的一致性.

1 循环平稳随机过程及谐波级数表示

1.1 循环平稳随机过程的定义

若一个随机过程x（t）的均值Mx（t）与时间有关，是时间t的周期函数，则称该随机过程为一阶循环平稳随机过程，即其均值满足

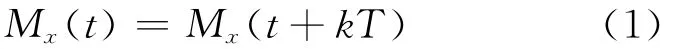
其中Mx（t）＝E［x（t）］，是随机过程x（t）的统计均值；T表示周期；k＝1，2，3，….

若一个随机过程x（t）的时变自相关函数定义为

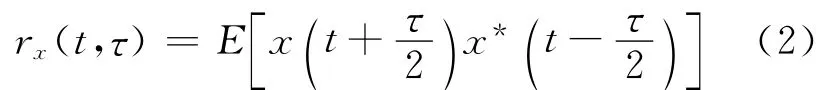
当对于每一个固定的延时τ，rx（t，τ）是关于时间变量t的周期函数，则称该随机过程是二阶循环平稳随机过程.既然rx（t，τ）是关于t的周期函数，rx（t，τ）可以表示为傅里叶级数的形式.令α＝n/T，n＝1，2，3，…，T是rx（t，τ）的周期，则有

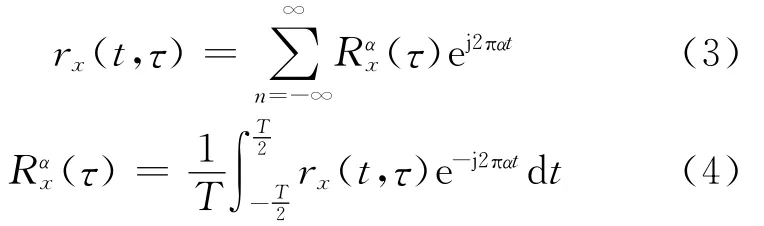
其中（τ）被称为循环自相关函数，α为循环频率.当α＝0时，Rαx（τ）就是通常的自相关函数.对于一个循环平稳随机过程而言，必定存在一个循环频率α≠0，使得循环自相关函数Rαx（τ）不为零.

1.2 循环平稳随机过程的谐波级数表示

由文献［1］可知，周期为T的循环平稳随机过程x（t）可以用一组联合平稳随机过程｛xp（t），p＝0，±1，…｝表示，即

其中

由式（6）可知，谐波级数表示中的第p个分量xp（t）ej2πpt/T可以看做是输入x（t）通过理想带通滤波器的输出.该带通滤波器的传递函数为

这样，从频域很容易理解谐波级数表示的本质，它是将x（t）分解为以1/T的整数倍频率为中心频率及带宽为1/T的分量之和.虽然式（5）适用于任意的随机过程，但它特别适用于周期为T的循环平稳随机过程，这时xp（t）之间是联合平稳的，它们之间存在相关性；当xp（t）之间不相关时，x（t）为平稳随机过程.

2 理论分析

循环平稳随机过程除了可以采用谐波级数表示外，周期时变参数模型（周期自回归模型、周期滑动平均模型以及周期自回归滑动平均模型）也是表示循环平稳随机过程的常用方法.接下来，将从循环平稳随机过程的谐波级数表示出发，证明通过适当的变换可以将谐波级数表示转化为相应的周期时变参数模型，进而得到一种求取循环平稳随机过程周期时变参数模型的方法.

对式（5）中的x（t）以Ts＝T/M为周期进行采样可得

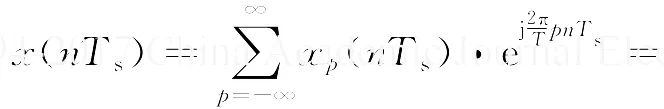
令p＝rM＋m，上式可化为

由于平稳随机过程的和还是平稳的，定义M个新的过程式（9）可化为

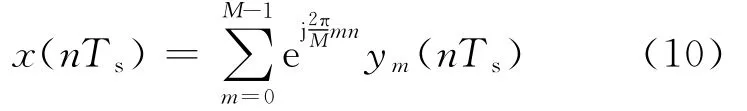
将nTs简写为n，并令n＝cM＋d，式（10）可以表示为

根据Wold分解定理，平稳随机过程ym（cM＋d）可以采用滑动平均（MA）模型来表示，即

其中w（·）为白噪声序列.将式（12）代入式（11）可得

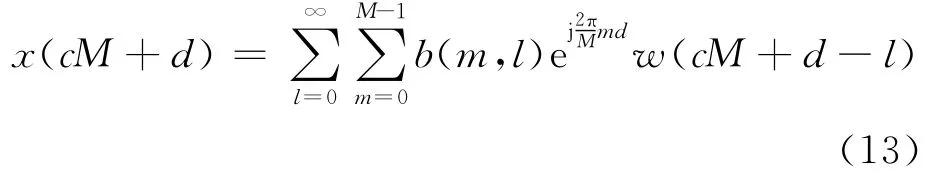
尽管式（13）中的b（m，l）是时不变的，但ej2πmd/M是时变的，因此式（13）本质上还是一个时变参数模型.另一方面，因为ej2πmd/M关于d的周期是M，因此也是周期的，令

因为b（d＋cM，l）＝ … ＝b（d＋M，l）＝b（d，l），所以式（13）可以表示成如下的周期滑动平均（周期MA）参数模型的形式：

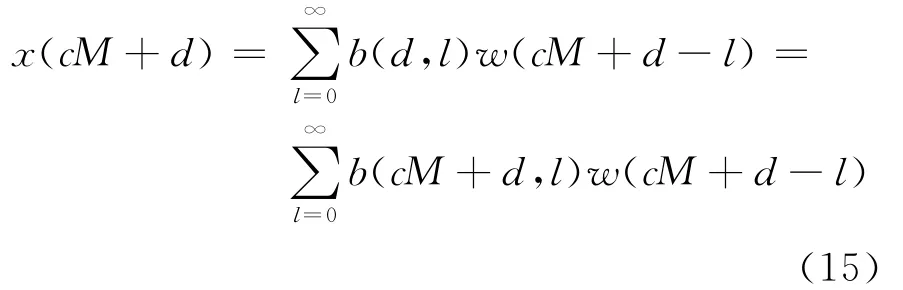
若令n＝cM＋d，则式（15）可以表示为

至此证明了由谐波级数表示可以获得相应的周期 MA参数模型.在假设多项式B（z）＝b（n，0）＋b（n，1）z－1＋…＋b（n，q）z－q＋… 所有的根都位于单位圆内时，式（16）所示的周期MA模型是可逆的，可以表示为如下周期自回归滑动平均（周期AR）模型形式：

其中每个a（n，i）均可由全部b（n，l）的某种函数来表示，由于b（n，l）是周期的，a（n，i）也是周期的，且它们的周期相同.周期自回归滑动平均（周期ARMA）模型是周期AR模型和周期MA模型之和，因此下面的周期ARMA模型将具有更广泛的代表性.

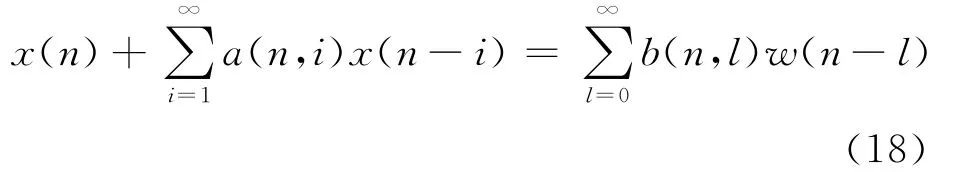
考虑到实际应用的需要，周期ARMA模型的阶数可以取保证一定精度情况下的有限值.设AR部分和MA部分的阶数分别为p和q，则式（18）所示的模型可以表示为

综上可知：对循环平稳随机过程的谐波级数表示进行适当的变换，可以得到相应的周期MA模型、周期AR模型和周期ARMA模型表示.

3 仿真研究

为了验证上述方法的正确性，对由循环平稳随机过程的谐波级数表示获得的周期MA参数模型的性能进行仿真.考虑如式（20）所示的谐波级数表示：

其中a（n）为平稳随机过程，该信号是按照如下方法产生的：首先产生一段在［－1，1］均匀分布的白噪声，将该白噪声通过传递函数为H（z）＝1/（1－0.9z－1）的低通滤波器后而得到.由式（20）可知，该循环平稳随机过程的归一化循环频率为α＝0.2，经过简单的推导可以得出其循环自相关函数为

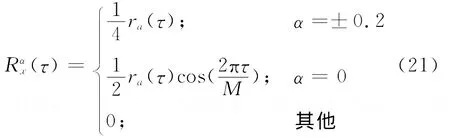
式中：ra（τ）为平稳随机过程a（n）的自相关函数，其表达式为

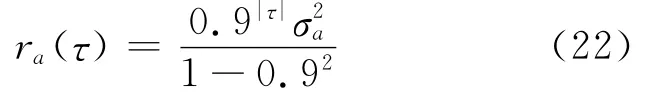
其中为平稳随机过程a（n）的方差.在仿真中＝0.33，样本点数为1 000，最大延时为40，归一化循环频率（按采样频率进行归一化处理）采样间隔为0.1，并采用高阶AR模型来逼近MA模型的方法建立平稳随机过程a（n）的MA模型，选择高阶AR模型的阶数为100，MA模型的阶数为16，当获得MA模型的参数估计后，采用式（16）构造周期MA模型，则所获得的周期MA模型输出信号的循环自相关函数如图1所示.

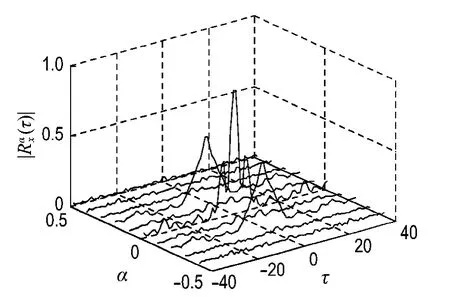
图1 循环自相关函数的幅值Fig.1 Amplitude of cyclic autocorrelation function

由图1可知，当α＝0和α＝±0.2时，周期MA模型估计的信号循环自相关函数不为零，而其他α值的循环自相关函数均为零，与式（21）所示的理论结果相一致，从而说明了本文方法的有效性.

为了进一步验证谐波级数表示与周期MA模型间的一致性，仿真中选取另外100组与辨识模型无关的样本进行模型校验，校验结果如图2所示，其横坐标为样本点数，纵坐标为输出信号的幅值.由图2可知，周期MA模型的输出与谐波级数模型的输出基本一致，从而进一步说明了本文方法的有效性.

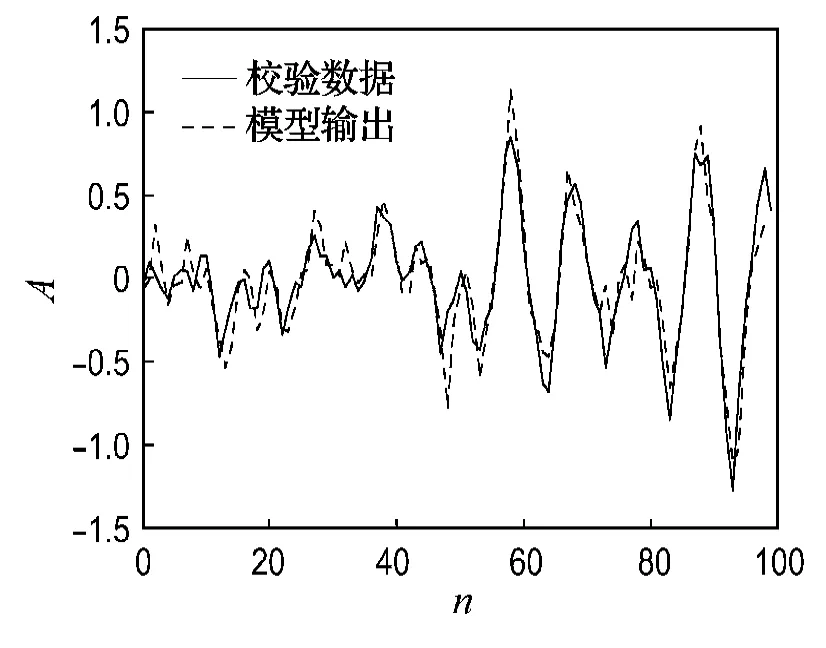
图2 模型校验结果Fig.2 Checked results of model

4 结 论

本文从循环平稳随机过程的谐波级数表示出发，给出了在一定精度要求下，由循环平稳随机过程谐波级数表示获得周期时变参数模型的方法，并通过仿真验证了该方法的有效性.

［1］王宏禹.非平稳随机过程分析与处理［M］.北京：国防工业出版社，1999：245－285

［2］JACHAN M， MATZ G， HLAWATSCH F.Time－frequency ARMA models and parameter estimators for underspread nonstationary random processes ［J］. IEEE Transactions on Signal Processing，2007，55（9）：4366－4381

［3］FARHOOD M，BECK C L，DULLERUD G E.Model reduction of nonstationary LPV systems［J］.IEEE Transactions on Automatic Control，2007，52（2）：181－196

［4］GAD E，NAKHLA M.Efficient model reduction of linear periodically time－varying systems via compressed transient system function ［J］.IEEE Transactions on Circuits and Systems，2005，52（6）：1188－1204

［5］陈 喆，王宏禹，邱天爽.适用于LPTV系统的周期自适应滤波器的研究［J］.电子与信息学报，2003，25（7）：884－891

［6］XI Feng，LIU Zhong.Modeling and prediction of cyclostationary chaotic time series using periodic autoregressive models［C］//International Conference on Communications，Circuits and Systems.Beijing：IEEE，2005：721－725

［7］XI Feng，LIU Zhong.Modeling and prediction of cyclostationary chaotic time series using vector autoregressive models ［C］// IEEE International Symposium on Signal Processing and Information Technology.Beijing：IEEE，2006：468－473

［8］MCLERNON D C.Relationship between an LPTV system and the equivalent LTI MIMO structure［J］.IEE Proceedings on Vision，Image and Signal Processing，2003，150（3）：133－141

［9］NGUYEN H H，NAMIHIRA Y.Electromagnetic field calculated by a new method of spreading variable［C］ // The First International Conference on Communications and Electronics.Hanoi：IEEE，2006：456－462

［10］KUDINTSEVA I G， MYAND S V，NICKOLAENKO A P，etal.Time domain solution for the natural sub－ionospheric ELF pulse ［C］//1998 International Conference on Mathematical Methods in Electromagnetic Theory.Kharkov：IEEE，1998：295－299