一类变幂率的无标度网络模型构建和分析

那 日 萨， 张 书 超， 穆 青

（大连理工大学 管理学院，辽宁 大连 116024）

0 引 言

现实世界中许多系统都可以用复杂网络来描述，20世纪末，Albert等在对互联网的研究中发现了无标度网络（scale－free network），即节点度分布服从幂律分布，从而开辟了人类对于复杂网络系统认识的新天地.

BA模型［1］是第一个无标度网络演化模型，它捕捉到了无标度网络形成的增长和择优连接这两个必不可少的机制，说明了大规模复杂网络自组织成为无标度状态的原因.BA模型虽然比较准确地把握了现实世界中网络最基本的特点，较好地解释了无标度网络的形成机制，但其与现实网络相比，仍有一定的差距，如多数现实网络具有很大的集聚系数，它们的度分布指数γ一般介于（2，3）［2～4］，相反BA 网络的集聚系数随着网络规模增大趋于0且其度分布指数γ＝3.

为了对现实的复杂网络进行更深入的分析和研究，还需要对BA模型进行扩充，使它更加符合实际.刘慧等［5］兼顾局域演化、增长，以及局域与局域外存在较弱连接等3方面因素的加权网络，发现它服从幂律指数为（2，3）的幂律分布.Krapivsky等［6］研究了非线性的择优连接机制，并证明线性择优连接时的幂率分布指数γ∈（2，∞）.Dorogovtsev等［7］考虑了老节点之间的连接或者断开的情况，用节点连通的平均度的变化率来建立模型，并计算出该模型的网络幂指数γ＝2＋1/（1＋2c），其中c∈R.Albert等［8］建立的模型则加入了一个老节点之间连接和已有边的重新连接这两种情况.但如何用连续域的解析方法建立和论证具有一般意义的复杂网络演化模型仍是需要解决的问题，这对于细致地分析复杂网络的演化过程具有重要意义.本文基于BA模型（新增节点的度为m），引入老节点之间的线性择优连接机制（每次新增p条边），建立一类变幂率的无标度网络模型，用连续域的方法［9］给出这类复杂网络演化的解析结果，并给出该网络的集聚系数；同时通过一些实际网络数据的分析，说明该网络模型的有效性和合理性.

1 模型的演化规则

BA模型只考虑了新加入节点与系统已存在节点的连接情况，忽略了系统已存的老节点间的连接情况，为此基于BA模型，本文引入老节点之间的连接机制，构建一类新的网络演化模型，其演化规则描述如下：

（1）在初始时刻t＝0，假定系统中已有少量（m0个）节点.

（2）t＝1时刻，新增一个度为m（m≤m0）的节点（与系统中原有的m0个初始节点进行连接，并且m0个孤立点之间产生p条边（p≤m0（m0－1）/2））.

（3）在以后每一个时间间隔内，向系统增加一个度为m的新节点，其m条边择优连接到网络中已经存在的不同节点上，并且现有系统老节点间择优产生p条边，直至网络达到所需要的大小为止.这样在经过t个时间间隔后，便形成一个具有N＝m0＋t个节点、（m＋p）t条边的网络.

具体的演化示意图见图1，初始时刻m0＝5，若m＝3，p＝2.t＝1时，新增节点5与节点0、1、4相连，老节点2与3、3与4之间产生p＝2条边.t＝2时，新增节点6与节点3、4、5相连，已有节点0与2、3与5产生p＝2条边.

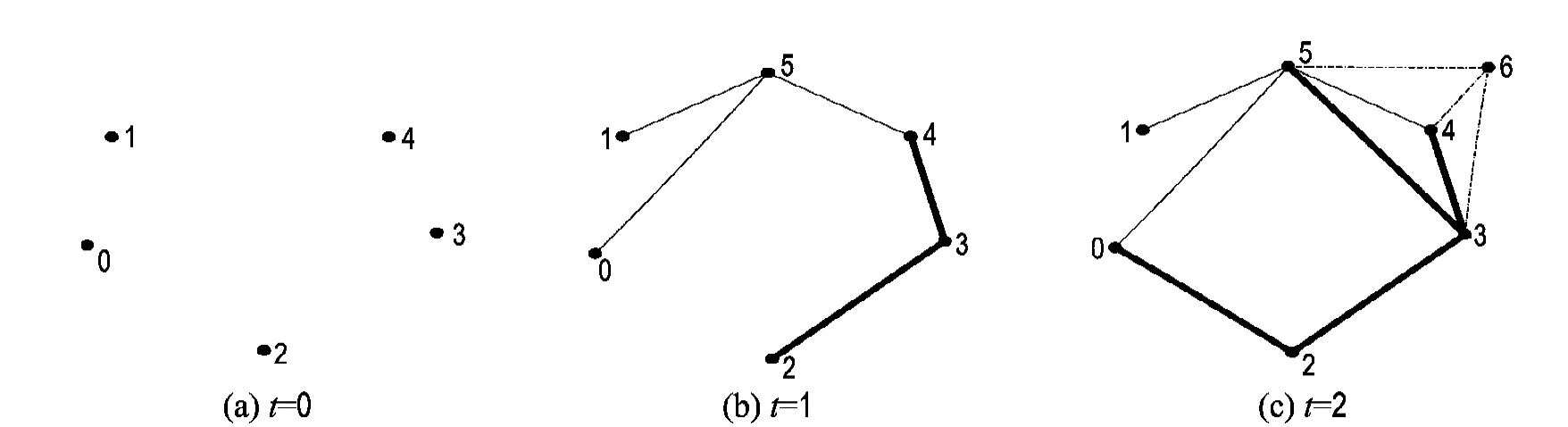
图1 网络演化示意图Fig.1 Sketch diagram of network evolution

下面给出该网络演化的解析方程.

2 网络模型的解析解及计算分析

在t时刻系统中有m0＋t个节点，设模型中i节点的连通度为ki（t）.根据前述演化规则，一方面考虑依据BA规则新增节点及其连接，一方面考虑老节点间的连接.

根据BA模型演化的择优连接规则，i节点与新增节点连接的概率为P i（t），其中Pi（t）取决于该节点的连通度，

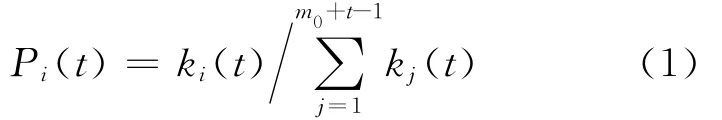
假设ki（t）连续，由于新增节点与老节点间的连接，以及老节点之间的连接均服从择优连接规则，对已有节点i，有

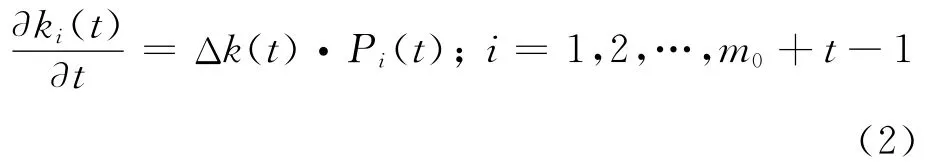
其中Δk（t）表示t时刻网络系统连通度的增量.在一个时间间隔网络系统连通度的变化Δk（t）由两部分构成，一是由新增节点增加的m条边导致的新增连通度m，二是由老节点产生p条边导致的新增连通度2p.因此有Δk（t）＝m＋2p，又考虑到则有

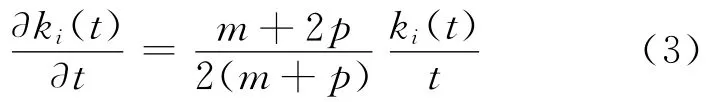
设节点i是t i时刻添加到系统的，则连通度ki（ti）＝m，此即为式（3）中微分方程的初始条件.通过计算，可得方程（3）的解

考虑节点连通度ki（t）小于k的概率P（ki（t）＜k）可表示为

假设时间t服从均匀分布，即

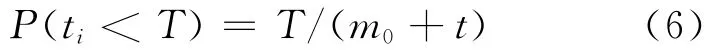
则

即

那么节点连通度的分布函数P（k）为

从中可得节点度分布呈幂率分布，其幂指数为

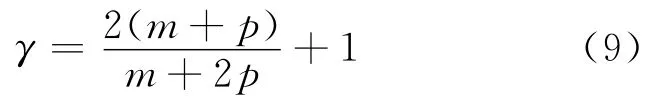
式（9）可改写为

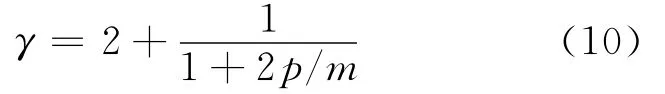
如果令c＝p/m，则式（10）与文献［7］的结果相同.由式（10），节点度分布的幂指数γ∈ （2，3］，这与目前实际网络幂指数的值是符合的.p与m取值不同时γ的变化如下：

（1）当p＝0时，γ＝3，即转化为BA模型；

（2）当pm时，即老节点连接的边远小于新节点连接的边时，γ接近3；

（3）当pm时，即老节点之间的连接远大于新加入节点产生的边时，γ接近2.

这说明，本文模型能够更好地描述实际网络演化问题，并且，BA演化模型只是其一个特例.

图2给出了选取不同的p、m下利用理论结果式（8）计算得到的节点连通度分布函数图形.

图2是初始有7个点按照本文所述的演化规则演化到10 000个点的网络后节点的度分布情况.

通过图2可以看出，在m＝3的情况下，随着p的增大，曲线斜率的绝对值减小，即随着p/m的增大，γ减小，结合式（10）可得γm＝3，p＝1＝2.6，γm＝3，p＝7＝2.18.图3给出了一个随机模拟节点连通度分布与理论分布函数比较的图.

通过图3可以看出，随机模拟理论模型的节点连通度的分布结果一致，此时理论节点度分布的幂率指数γm＝3，p＝1＝2.6.

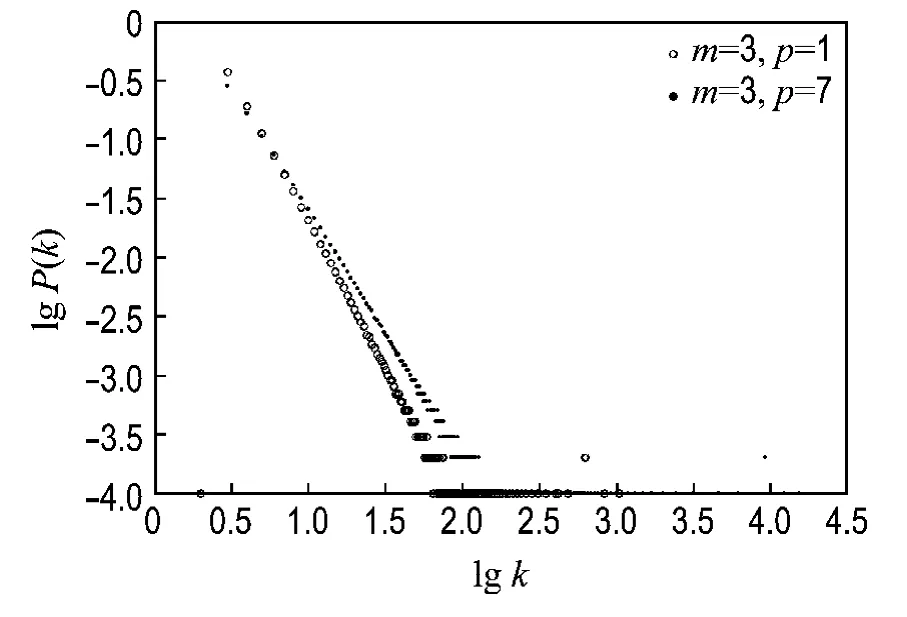
图2 不同的p、m下节点连通度分布函数图形Fig.2 The diagram of distribution function of node connectivity in different p，m

图3 连通度分布与理论分布的比较（m0＝5，m＝3，p＝1）Fig.3 The comparison of connectivity distribution and theoretical distribution function（m0＝5，m＝3，p＝1）

3 网络的集聚系数和平均路径

根据定义，节点i的集聚系数Ci等于它的k i个直接邻居之间实际存在的边数E i占所有可能存在 的 边 数k i（ki－1）/2 的 比 例，即Ci＝2Ei/［ki（ki－1）］.整个网络的集聚系数指的是所有节点集聚系数的算术平均值.可见，Ci只与两个变量E i和k i有关，只有当Ei和k i变化时，Ci才随着改变.章忠志等［9］曾给出与BA网络等价的一个网络的集聚系数.由于在本模型中，只有新节点与老节点之间才建立连接，当新节点连接到节点i且与i的邻居进行连接时，或者节点i的邻居之间发生连接时，节点的ki和E i会发生改变，从而改变Ci的值.Ci满足下面的动态方程：

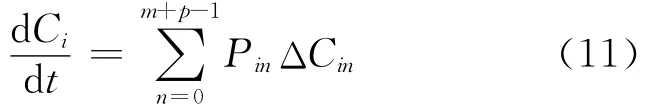
其中ΔCin表示新节点连接到节点i和它的n个邻居时集聚系数的变化值，Pin表示这一变化的概率.ΔCin满足下式：

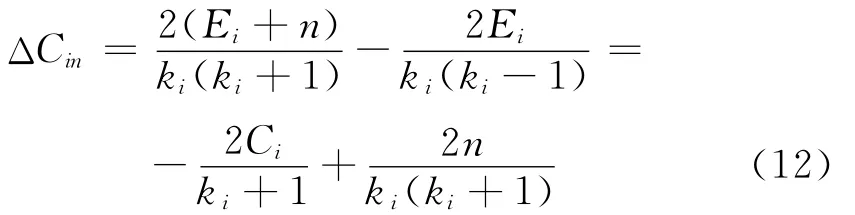
Pin由两部分的乘积构成：第1部分是有一条新边连接到节点i的概率，这一概率由式（3）给出；第2部分指的是其余（m＋p－1）条新边连接到节点i的n个邻居的概率，它等价于每次成功概率为n（i）/（2m＋2p）t的（m＋p－1）重贝努利试验中，成功n次的概率.n（i）表示节点i的邻居数目，其值可通过下面的积分获得.

综上可得Pin的关系式为

由式（14）知：n＞1时，Pin很小，可以忽略.将式（4）、（12）、（14）代入方程（11），忽略低阶项，得

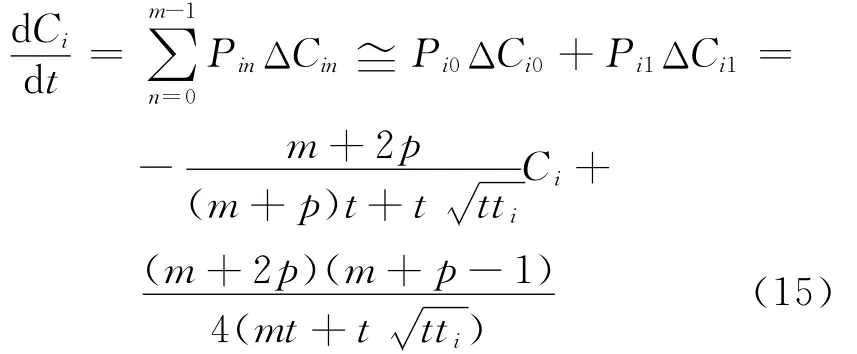
由式（15），可得到Ci随时间的演化公式：

对式（16）进行积分计算，就可得到整个网络的平均集聚系数

可见，根据该演化模型，可推定其平均集聚系数随着网络规模的增大而迅速下降.当p＝0时，

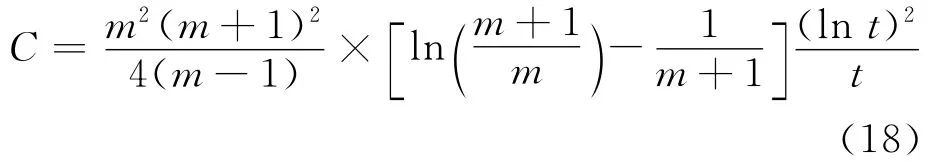
由式（18）知该演化模型的平均集聚系数与BA网络完全相同，BA模型只是该演化模型的特例.

网络的平均路径长度是指网络中所有节点对之间的平均最短距离，它描述了网络节点之间的分离程度.这里节点间的距离指的是从一节点到另一节点所要经历的边的最小数目.平均路径长度的计算公式为，其中d ij为节点i和j之间的最短距离，N为网络的规模.关于随机网络平均路径长度的解析计算，目前还没有普适的一般性方法.BA模型平均路径的较精确解直到最近才被Chen等［10］给出，可见复杂网络平均路径长度求解的困难.在今后的工作中，将对本文模型的平均路径长度的解析计算进行深入研究.

4 几个实际网络参数的估计

在现实生活中，实际的许多网络如电影演员合作网等呈现出无标度现象，这些网络相应规模下的幂率分布指数和节点平均连通度见表1.

表1 实际网络的无标度现象Tab.1 The scale－free phenomenon in the real networks

这里假设实际的网络是由BA模型演化而来，设网络初始有m0个节点，经过w时间，则有〈k〉＝2mw/（m0＋w），当w→∞时，m则近似为实际网络的平均度〈k〉的1/2，将m、γ代入式（10）可以计算出p.本文模型是同时考虑新增节点产生连接和老节点间的连接，则有〈k〉＝2（m＋p）w/（m0＋w），所以可近似地认为〈k〉＝ （m＋p）/2，这样可以由算出的p和〈k〉推出m的值，结合式（10）可得本文模型的γ，具体结果见表2.

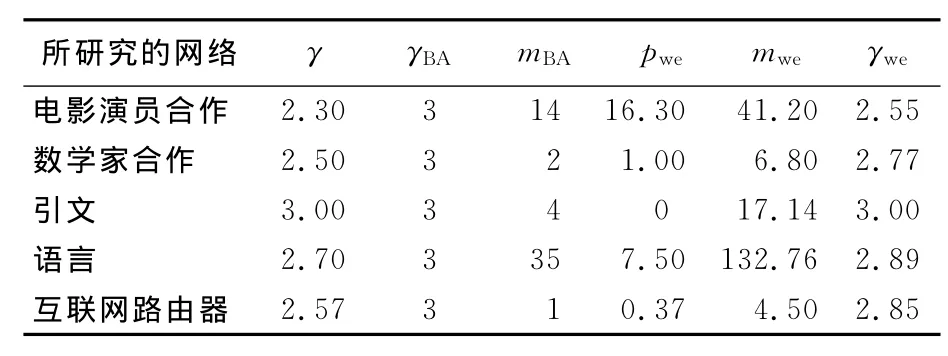
表2 实际网络参数的估计Tab.2 The estimation of parameters on the real networks

表2中γBA表示BA模型推出的幂率分布指数，mBA表示假设实际网络遵照BA模型演化时近似推得的BA模型中的m值，pwe表示由γ、mBA结合式（10）计算的p值，mwe是根据pwe和〈k〉近似得到的本模型中m值，γwe则是将pwe、mwe代入式（10）计算得到的本模型的幂率分布指数值.

通过表2可以看出本模型所得到的幂率分布指数比BA模型更接近于实际网络，从而也证明了本模型的合理性和适用性.

5 结 语

用连续域的解析方法建立和论证具有一般意义的复杂网络演化模型，对于分析大规模复杂网络的演化规律、准确计算网络各项综合指标（如集聚系数）具有重要意义.本文提出了一类变幂率的无标度网络模型，模型在BA模型的基础上，加入系统已存节点之间的连接（其连接隐含择优连接机制），并用连续域方法给出了该模型节点连通度分布函数的解析解和网络的集聚系数.通过模拟计算分析，验证了本文所提出的变幂率的网络模型为无标度网络，并且其幂率为2（m＋p）/（m＋2p）＋1，通过调节m和p的值，可以让其幂率在（2，3）变化.当p＝0时，该模型与BA模型是一致的.通过一些实际网络的数据，近似计算出本模型的幂率分布指数，验证了该模型较之BA模型更具合理性和有效性.当然这里仅考虑了老节点之间产生新连接的问题，现实网络涉及的其他问题并没有加入到模型中，在今后的研究中，将进一步完善.

［1］BARABSI A L， ALBERT R， JEONG H.Mean－field theory for scale－free random networks［J］.Physica A，1999，272（68）：173－187

［2］ALBERT R，BARABSI A L.Statistical mechanics of complex networks［J］.Reviews of Modern Physics，2002，74（1）：47－97

［3］DOROGOVTSEV S N，MENDES J F F.Evolution of networks［J］.Advances in Physics，2002，51（4）：1079－1187

［4］NEWMAN M E J.The structure and function of complex networks［J］.SIAM Review，2003，45（2）：167－256

［5］刘 慧，李增扬，陆君安.局域演化的加权网络模型［J］.复杂系统与复杂性科学，2006，3（1）：36－43

［6］KRAPIVSKY P L，REDNER S，LEYVRAZ F.Connectivity of growing random networks ［J］.Physical Review Letters，2000，85（21）：4629－4632

［7］DOROGOVTSEV S N，MENDES J F F.Scaling behaviour of developing and decaying networks［J］.Europhysics Letters，2000，52（33）：33－39

［8］ALBERT R，BARABASI A L.Topology of evolving networks：local events and universality ［J］.Physics Review Letters，2000，85（24）：5234－5237

［9］章忠志，荣莉莉.BA网络的一个等价演化模型［J］.系统工程，2005，23（2）：1－5

［10］CHEN Fei，CHEN Zeng－qiang，WANG Xiu－feng，etal.The average path length of scale free networks［J］. Communications in Nonlinear Science and Numerical Simulation，2008，13（7）：1405－1410

［11］BARABSI A L， ALBERT R.Emergence of scaling in random networks ［J］.Science，1999，286（5439）：509－519

［12］NEWMAN M E J. Scientific collaboration networks.I.Network construction and fundamental results［J］.Physics Review E，2001，64（1）：016131

［13］CANCHO R F I，SOLE R V.The small－world of human language ［J］. Proceedings of the Royal Society B，2001，268（1482）：2261－2265