孔隙湿度对混凝土初始弹性模量影响

白 卫 峰， 陈 健 云， 孙 胜 男

（1.大连理工大学 建设工程学部，辽宁 大连 116024；2.华北水利水电学院 钢结构与工程研究所，河南 郑州 450011；3.聊城大学 建筑工程学院，山东 聊城 252059）

0 引 言

混凝土是由水泥、水、粗细骨料人工合成的复合材料，待硬化成型后细观结构包括灰泥、粗骨料和孔隙三相；混凝土材料宏观力学性能由细观各相介质的体分比和界面特性共同决定.其中细观孔隙对混凝土力学性能产生重要的影响.普通混凝土作为典型的多孔性复合材料，孔隙率一般不小于8%～10%.孔隙可分为两类[1]，一类为活性孔隙，呈毛细管状分布，尺寸10 nm～10μm，在水环境中可由孔隙水填充，因此活性孔隙体系受到混凝土加工时间、湿度和暴露工况共同作用，对混凝土的力学性能和耐久性产生重要的影响；另一类为非活性孔隙，尺寸0.5～4.0 nm，呈球状分布，加工成型后由气泡填充，不受环境湿度和暴露条件的影响，孔隙水不能渗入.在基础结构的设计当中，为提高混凝土材料的抗冻融特性，常采用引气混凝土.对于这类混凝土，当中的非活性孔隙所占体分比具有相当的比重，能够产生均匀、稳定、封闭、互不连通的微小气泡，避免了毛细管道的形成，缓和了孔隙水的影响[2].

在水环境中工作的混凝土强度降低，弹性模量升高.Yaman等[1]的试验表明，在同一孔隙率下，与干燥混凝土相比，饱和混凝土的泊松比和弹性模量有所增大；同时在试验中详细记录了两种类型微孔隙的体分比，以及对混凝土初始模量产生的总体效果.研究表明[3]，混凝土材料的弹性模量和强度等力学性能随非活性孔隙体分比的增长呈现成比例减小的趋势，并受活性孔隙体分比及其饱和度的影响.因此有必要区分开两类孔隙并分别加以考虑其对材料力学性能的影响.

考虑到混凝土作为典型的多相复合材料，许多学者采用细观力学的等效夹杂理论预测材料的力学性能.对于干燥混凝土，Yang等忽略微孔隙的影响，建立了单夹杂模型[4]和双夹杂模型[5]；Nilsen等[6]建议模型应该考虑灰泥、骨料和过渡区域三相.对于湿态饱和混凝土，Yaman等[1]和王海龙等[7]分别采用 Kuster－Toksoz（K－T）方法和Mori－Tanaka（M－T）方法建立了单夹杂模型.在众多夹杂问题求解的方法中[8、9]，M－T 方法物理概念清晰，解答较为合理，便于实际应用，被广泛地应用于各种复合材料有效性能的预测.本文尝试采用M－T平均应力场概念下的等效夹杂方法，建立双类软化夹杂模型（理想无孔隙混凝土为基体、活性和非活性孔隙为两类软化夹杂），区分两类微孔隙在不同饱和度条件下的影响，预测混凝土材料力学性能.

1 双类软化夹杂模型

图1为本文采用的混凝土代表体积单元模型示意图.此模型中，将理想混凝土固相（灰泥和粗骨料的复合体，认为两者无缺陷地粘结在一起）看做是一种均匀弹性材料，作为基体；两类孔隙分别作为两类弹性软化夹杂，均匀嵌入在基体当中.干燥条件下，两类孔隙均由空气填充；湿态环境下，活性孔隙则改由孔隙水填充.Km、Ki1、Ki2分别表示混凝土基体相和一、二类夹杂的体积模量；Gm、Gi1、Gi2分别表 示三相的剪切模量；fm、fi1、fi2分别表示三相的体分比.满足fm＝1－fi1－fi2（1）

1.1 饱和混凝土初始模量预测

首先考虑饱和混凝土的情况，定义g为饱和度，满足

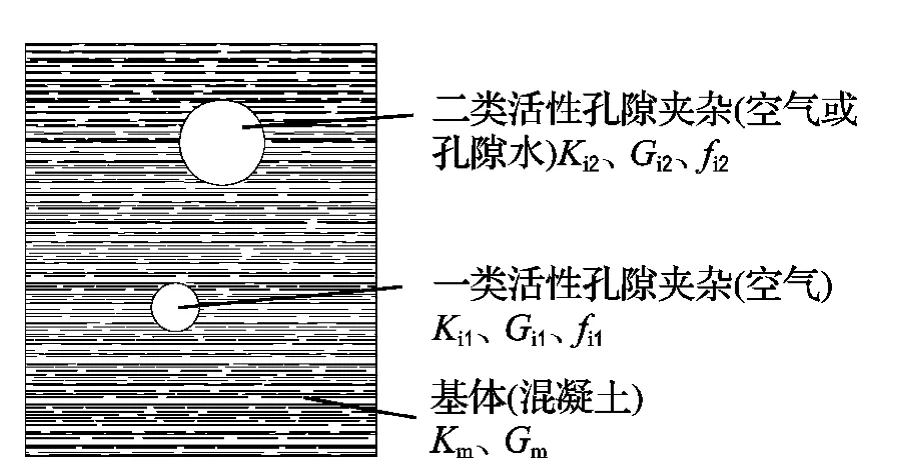
图1 混凝土代表体单元示意图Fig.1 Sketch map for representative volume of concrete

其中fw代表孔隙水的体分比.饱和情况下，g＝1.

首先不考虑夹杂的存在，假设混凝土代表体单元完全由理想均质基体填充，则在远场均匀应力σ作用下的本构关系可表示为

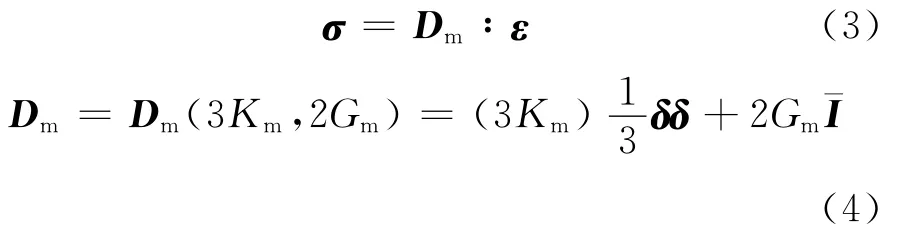
式中：Dm为混凝土基体的弹性张量；ε为基体对应应变；珔I为四阶等同单位张量.

由于夹杂的存在，实际复合材料基体内的应变场与均匀纯基体内的应变场相差一个扰动值εm，相应的扰动应力为σm，则实际基体内平均应力为

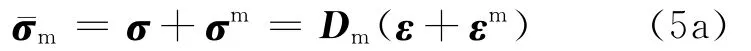
或

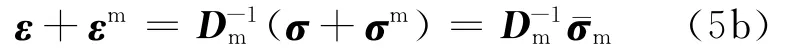
两相孔隙夹杂内的应变和应力场不同于基体，假设分别相差ε′i1、ε′i2和σ′i1、σ′i2.夹杂的应力扰动问题可以采用Eshelby等效夹杂理论处理，两相夹杂的平均应力珔σi1和珔σi2可表示为

协调柔性可以划分为：企业面对动态变化的环境，能够敏锐捕捉机会，比潜在及现有竞争对手更快地做出调整；企业能够更快地寻找到新的资源，并将其进行整合；企业能够比潜在及现有竞争对手更快地进入新市场；企业能够在多变的环境中高效利用资源。

其中Di1、Di2为两相夹杂的弹性张量；ε＊i1、ε＊i2为两相夹杂的等效特征应变.满足

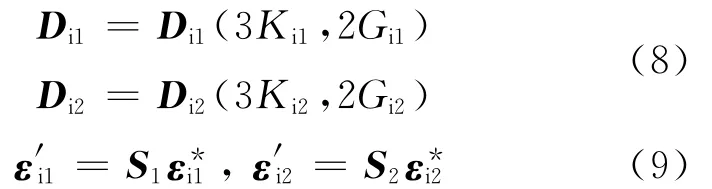
其中S1、S2为四阶Eshelby张量，与基体的弹性性质及夹杂物的形状有关.

令

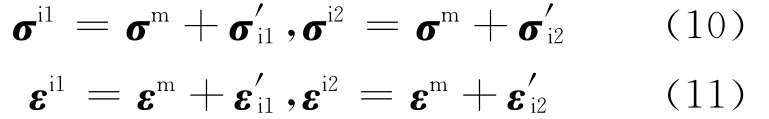
则σm、σi1、σi2分别为基体、一类夹杂、二类夹杂的扰动应力；εm、εi1、εi2分别为基体、一类夹杂、二类夹杂的扰动应变.

根据M－T方法平均应力场的概念，代表体单元中的平均扰动应力为零，满足

将式（9）、（10）代入式（6）、（7）得

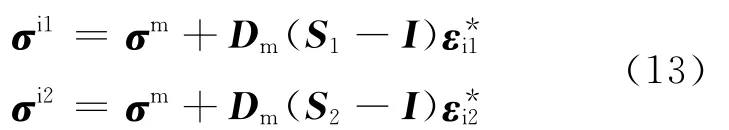
由式（12）、（13）得

将式（14）代入式（6）、（7），求解得到

其中

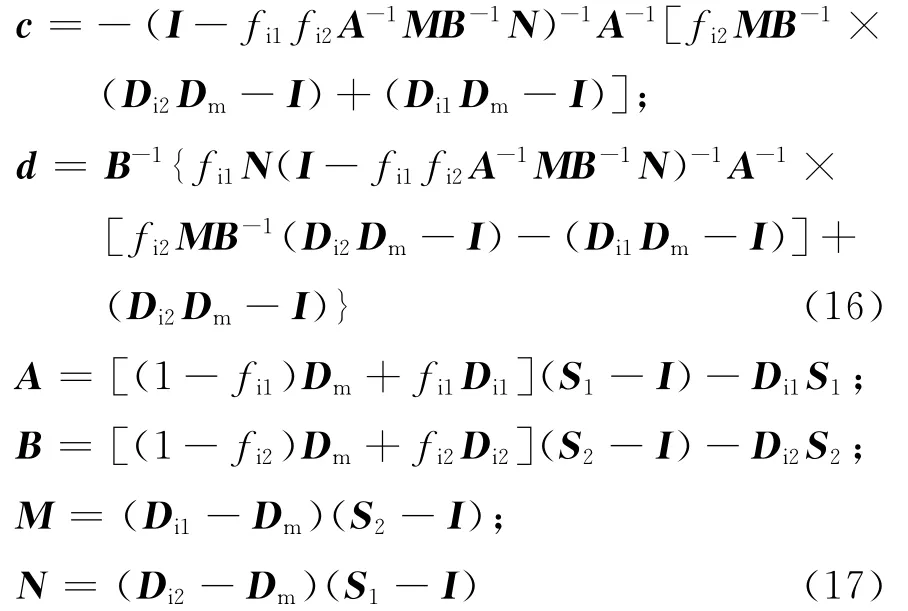
根据式（5）、（9）、（11）、（15），代表体单元整体的平均应变珔ε可表示为

其中珚D表示混凝土材料代表体单元等效弹性张量.则可得

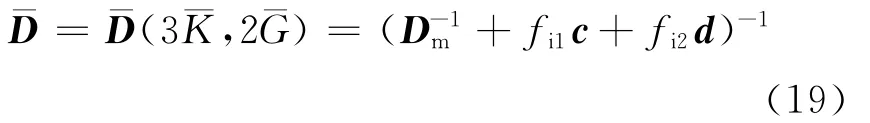
和表示孔隙混凝土的等效体积模量和剪切模量.

忽略两类孔隙大小、形状的区别和影响，均采用圆球形状模拟，Eshelby张量可表示为

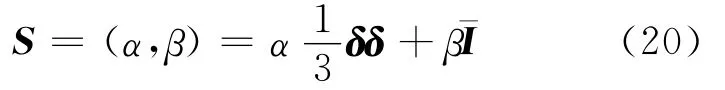
其中

根据四阶各向同性张量的乘法规则：若N＝N（a，b），K＝K（c，d），则N∶K＝ （ac，bd）.由式（19）可得孔隙混凝土材料的等效体积模量和剪切模量分别为

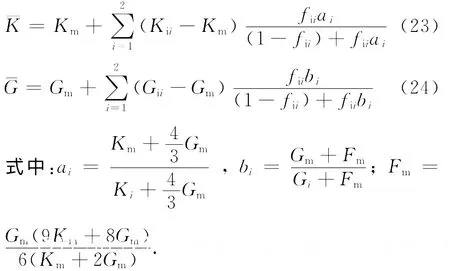
由弹性力学可得缺陷混凝土的弹性模量为

对于饱和混凝土，活性孔隙完全被孔隙水填充，fw＝fi2.由式（23）、（24）可知，只要知道了理想混凝土基体相的体积与剪切模量（即混凝土对应孔隙率为0的相应模量）、两相孔隙夹杂的体分比、空气和孔隙水的体积和剪切模量，就可以预测饱和混凝土的等效体积和剪切模量.

由于长期的水化作用，饱和混凝土的活性孔隙率和孔隙直径与干燥情况下相比均变小，饱和混凝土的有效活性孔隙体分比采用

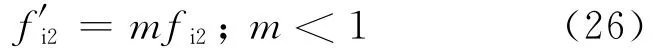
计算.由微观流体力学可知孔隙水存在较大的表面张力和粘滞力；同时考虑到进一步水化作用，使得孔隙水对混凝土的剪切模量有所贡献，参考文献［7］，本文通过拟合Yaman等的试验结果［1］得到如下以fi2为自变量计算饱和混凝土等效剪切模量珚的经验公式：

1.2 不同湿度混凝土初始模量预测

在实际试验中，通常采用饱和湿度混凝土研究孔隙水对材料力学性能的影响，忽略了不同饱和度情况的影响.而实际处于水环境中结构的不同部位往往处于不同饱和度的湿度状态；在饱和湿度和常态湿度之间存在一个过渡区域，采用有限元方法进行分析时，为准确模拟结构的受力状态，需要预测出这一区域材料的初始模量.本文采用近似方法预测不同饱和度情况下混凝土材料的初始模量.

对于任意非饱和湿度情况，0＜g＜1.若不考虑水化作用以及两类孔隙大小和形状的区别，则fw＝gfi2；非活性孔隙的体分比可采用f′i1取代fi1，即

有效的含水活性孔隙体分比为

代入式（23）可得等效体积模量.

等效剪切模量表示为

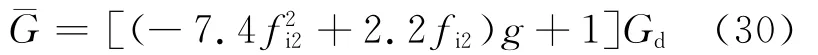
2 计算结果分析

构造算例，用本文模型计算结果与Yaman等[1]的试验结果进行比较分析.文献中通过回归分析得到的理想无孔隙混凝土材料参数以及推荐采用的基本参数见表1.文献中详细记录了不同孔隙率情况下（包括活性孔隙体分比和非活性孔隙体分比）干燥与饱和混凝土初始力学模量的试验结果.利用本文模型计算相同孔隙率条件下饱和和干燥混凝土的系列初始模量，比较结果见表2.计算中，m取0.8.

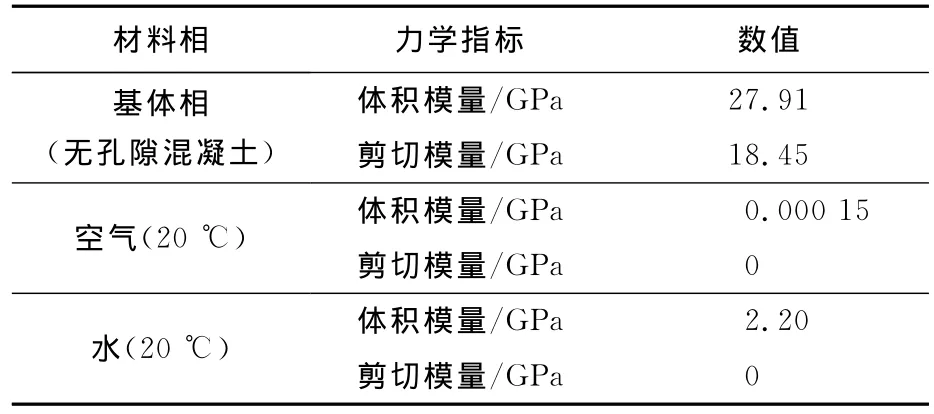
表1 混凝土三相的材料特性Tab.1 Properties of the three phases of concrete

表2给出了不同孔隙率条件下（包括不同的非活性孔隙率和活性孔隙率）干燥混凝土和饱和混凝土弹性模量的计算结果和试验结果的对比情况.图2显示了在两种孔隙体分比不变的情况下，不同饱和度对混凝土材料弹性模量的影响情况，可以发现随着饱和度的增加，混凝土的弹性模量大致呈线性增长.

表2 干燥和饱和混凝土理论和试验参数结果比较Tab.2 The comparison of properties of dry and saturated concrete between theoretical and experimental results

通过分析可得出：两种类型的孔隙含量以及孔隙水含量对混凝土的体积模量、剪切模量以及弹性模量有较大的影响.随着孔隙含量的增加，干燥混凝土的弹性模量明显减小.相同孔隙含量的混凝土材料饱和情况和干燥情况相比，饱和情况下，其中的活性孔隙由孔隙水填充，这部分孔隙水使得饱和混凝土的弹性模量明显高于干燥混凝土.而非活性孔隙不能填充孔隙水，因此不论干燥或者饱和情况，非活性孔隙率对混凝土弹性模量的影响可以认为是不变的.饱和混凝土和干燥混凝土弹性模量的区别是由于活性孔隙中填充的孔隙水所引起的.

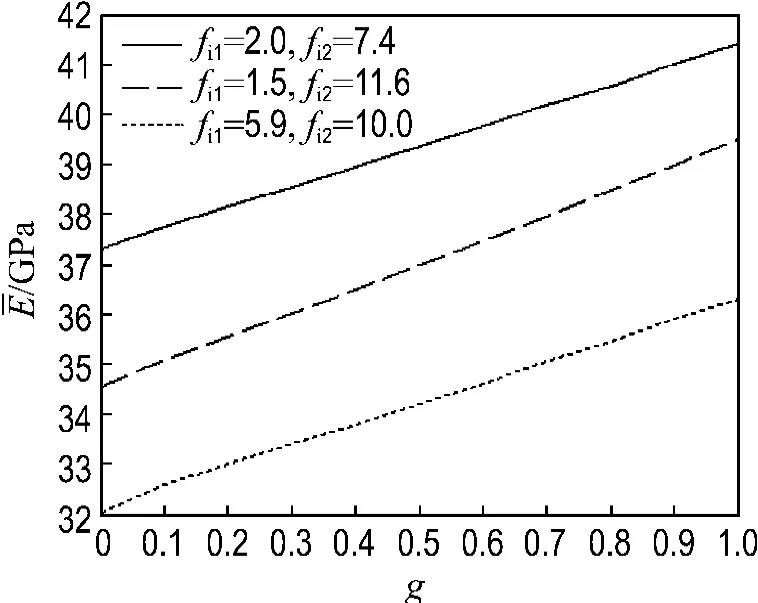
图2 不同饱和度情况下的混凝土弹性模量Fig.2 The elastic modulus of concrete undervariational saturation degrees

对于干燥混凝土，本文理论模型的计算结果与试验结果相比大致相符略微偏高.而对于饱和混凝土的情况，理论结果与试验结果吻合较好.在文中没有考虑两种孔隙的大小、形状对混凝土力学性能的影响.总之，孔隙水对混凝土力学性能的影响是一个复杂的物理化学过程，很难精确地模拟其效果.进一步的研究需要充分考虑水化作用的影响，根据试验结果拟合出以活性孔隙率为自变量的更加精确的经验公式.

3 结 论

基于等效夹杂理论和 Mori－Tanaka平均场的思想，本文采用细观力学方法建立了一种双类夹杂模型，用于探讨混凝土材料孔隙以及孔隙水对材料力学性能的影响机理.将细观孔隙区分为活性孔隙和非活性孔隙，并分别作为两类软化夹杂；活性孔隙可由孔隙水填充.本文模型物理意义明确，便于实际应用，可以预测不同饱和度情况下混凝土材料的初始参数，也可以用来解释孔隙和孔隙水的影响机理；特别适合于分析引气混凝土含水率对材料初始模量的影响.

随着孔隙率的增长，混凝土的弹性模量明显减小.由于非活性孔隙不能渗入孔隙水，在干燥或不同湿度情况下，这部分孔隙对混凝土力学性能的影响可以认为是不变的.在湿环境中，活性孔隙中渗入了孔隙水，使得这部分孔隙对材料力学性能的影响增大，增大了材料的力学模量；同时更主要的是，由于渗入的这部分孔隙水所产生的水化作用，改变了这部分活性孔隙率、孔隙尺寸和孔隙的形状以及产生的粘滞力和表面张力，使得湿态情况下混凝土的力学模量较干燥情况下增大的幅度更显著.

[1]YAMAN I O，HEARN N，AKTAN H M.Active and non－active porosity in concrete， Part II：Evaluation of existing models [J]. Materials and Structure，2002，35（3）：110－116

[2]商怀帅.引气混凝土冻融循环后多轴强度的试验研究 [D].大连：大连理工大学，2006

[3]MEHTA P K， MONTEIRO P J M.Concrete：Structure，Properties，and Materials[M].2nd ed.New Jersey：Prentice－Hall Inc.，1993

[4]YANG C C，HUANG R.A two－phase model for predicting the compressive strength of concrete[J].Cement and Concrete Research， 1996，26（10）：1567－1577

[5]YANG C C，HUANG R.Double inclusion model for approximate elastic moduli of concrete material[J].Cement and Concrete Research，1996，26（1）：83－91

[6]NILSEN A U，MONTEIRO P J M，GJORV O E.Estimation of the elastic moduli of lightweight aggregate[J].Cement and Concrete Research，1995，25（2）：276－280

[7]王海龙，李庆斌.饱和混凝土的弹性模量预测[J].清华大学学报，2005，45（6）：761－763

[8]黄克智，黄永刚.固体本构关系[M ].北京：清华大学出版社，1999

[9]杨庆生.复合材料细观结构力学与设计[M].北京：中国铁道出版社，2000