市场细分网站竞争模型及其稳定性分析

任 雅 威， 杨 德 礼， 刁 新 军

（大连理工大学 系统工程研究所，辽宁 大连 116024）

0 引 言

进入网络时代，人们的日常生活与互联网上形色各异的网站联系日趋紧密，与网站竞争相关的研究也引起了国内外众多学者的广泛关注.Maurer等［1］首先提出了一类网站动态竞争模型，并指出该模型中竞争的激烈程度不同会导致多个网站共享市场或者少数霸主赢家通吃的局面.文献［1］的工作表明互联网市场的主要特征可以通过一个基于Lotka－Volterra系统的网站竞争模型再现.这一模型可以表示为一个n元非线性微分方程组：

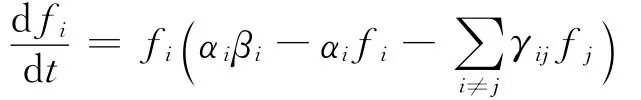
其中fi是网站i的市场占有率；αi是网站的增长率；βi是网站i的饱和市场占有率；γij表示网站i和j之间的竞争率，γij越大则由于网站j的存在而导致网站i的用户流失比率就越大.文献［2、3］的研究表明当同时引入竞争与合作机制时，文献［1］中模型会呈现出一些独特的现象；文献［4］放宽了文献［3］中模型的假设条件，并给出了完整的竞争策略分类；文献［5］考虑了竞争过程中的时滞；文献［6、7］强调了电子商务网站竞争过程中强者愈强的效应，给出了电子商务网站的竞争模型.

任何网站竞争模型都不能面面俱到，而只能是对特定假设前提下的现实网站竞争过程的抽象描述.本文考虑市场中存在细分市场的网站竞争模型，研究何时网站应该专注于细分市场，何时不应该进行市场细分.

1 市场细分的网站竞争模型

考虑n个网站竞争的情况，有r个网站的目标用户分布在整个市场中，而剩下的n－r个网站其用户分布在占整个市场θ份额的细分市场中.假设细分市场中的网站不参与细分市场以外的竞争，而目标市场为整个市场的网站同时参与细分市场的竞争.为了便于入手，不妨把整个问题分为两个子问题.

（1）在非细分子市场中，有r个网站争夺容量为1－θ的子市场份额，r个网站的竞争模型为

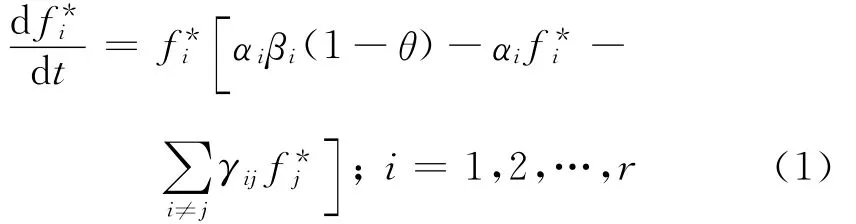
（2）在细分子市场中，有n个网站争夺容量为θ的子市场份额，n个网站的竞争模型为

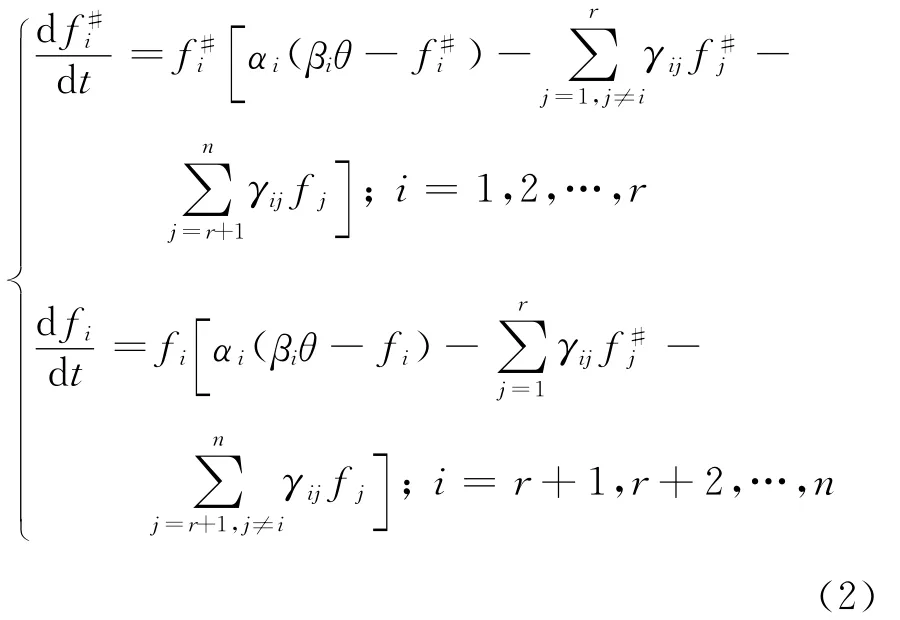
其中fi＃＝θfi且0≤fi＃≤θ，是网站i在细分子市场中的占有率.

系统（1）、（2）分别描述了两个子市场中网站竞争的情形.对于整个市场而言，当时.因此结合系统（1）、（2）就可以给出市场细分的网站竞争数学模型：

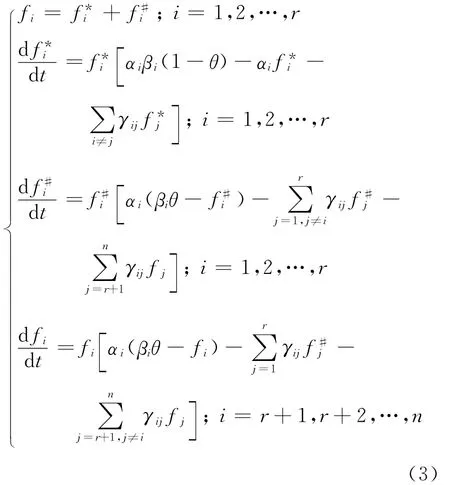
2 3个站点竞争的情况

对于模型（3）所描述的非线性系统，从最简单的而又足以说明问题的情形入手.考虑3个网站组成的系统，其中2个网站采用全市场策略，1个网站采用细分市场策略.网站1、2的目标用户分布在整个市场中，而网站3的目标用户则分布在市场容量为θ的细分市场中.

此时，在非细分子市场中，子系统模型为

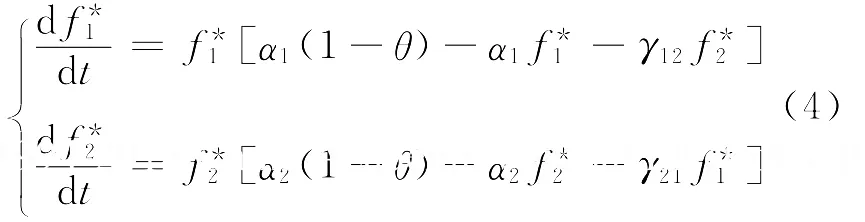
在细分子市场中，子系统模型为

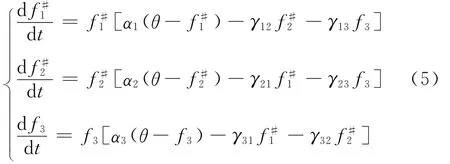
结合系统（4）、（5）从而得到存在细分市场的三网站竞争系统的模型为

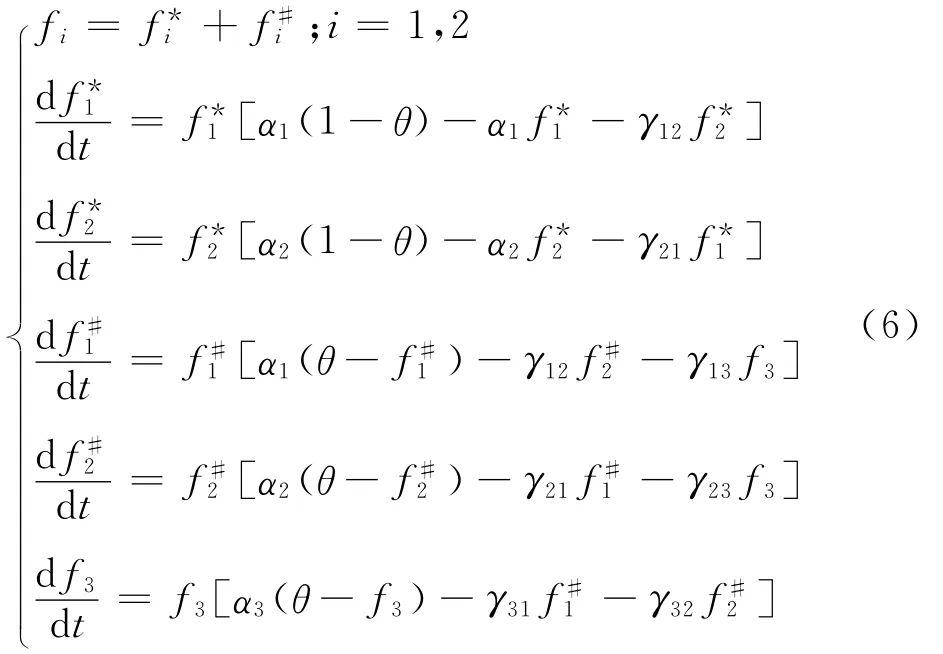
2.1 非细分市场中的情形

要研究系统（6）所描述的模型，不妨首先分别分析系统（4）、（5）.易知系统（4）的奇点有4个，分 别 为

下面分析各奇点的稳定性.系统（4）对应的Jacobi矩阵可表示为

将点P1、P2、P3、P4分别代入即可得到各个奇点所对应的Jacobi矩阵.为讨论系统（4）平衡点的局部稳定性，计算其在各平衡点处的Jacobi矩阵的特征根.

系统（4）在P1点处的Jacobi矩阵的特征根，由α和θ的取值范围可知，因此P1点为不稳定结点.

系统（4）在P4点处的Jacobi矩阵的特征根分别为和，此时，当时不全为负，P4点是不稳定奇点；当时点为稳定结点.

结合以上分析，对于系统（4）可以得出如下引理.

（2）当α/γ＞1时，P4点为稳定结点，P2、P3点是不稳定奇点.

此时对系统（4）进行数值仿真其相图如图1所示.系统（4）在不同条件下的竞争过程如图2所示.

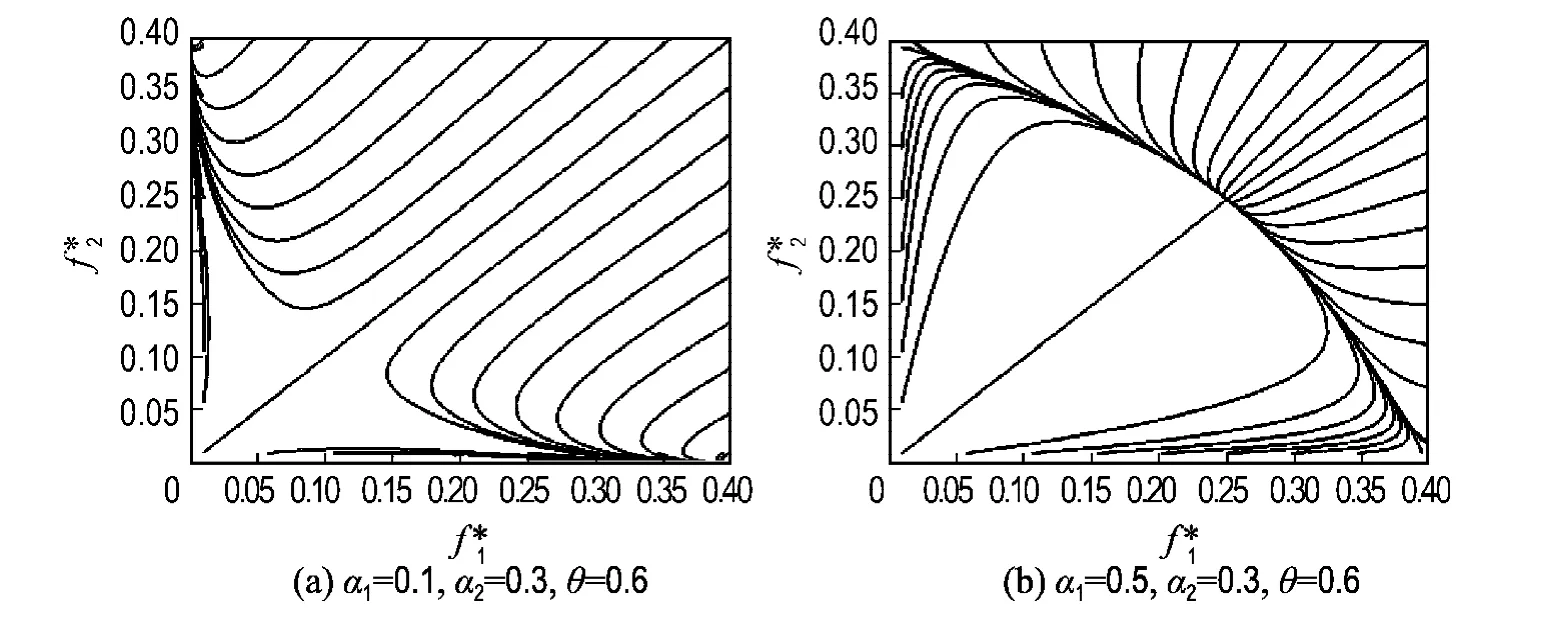
图1 系统（4）的相图Fig.1 Phase diagram of System （4）

图2 系统（4）的网站竞争过程示意图Fig.2 Schematic of competitive processes between websites of System （4）

2.2 细分市场中的情形

下面分析各奇点的稳定性.系统（5）对应的Jacobi矩阵可表示为将点分别代入即可得到各个奇点所对应的Jacobi矩阵.为讨论系统（5）平衡点的局部稳定性，计算其在各奇点处的Jacobi矩阵的特征根.

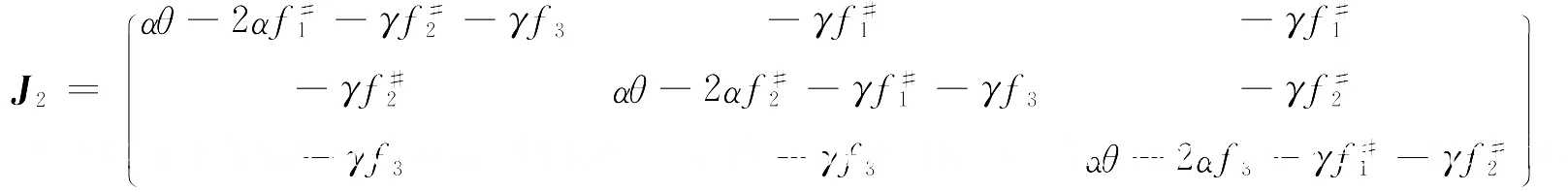
系统（5）在Q1点处的Jacobi矩阵的特征根，由α和θ的取值范围可知λ1，λ2，λ3＞0，因此Q1点为不稳定结点.

系统（5）在Q8点处的Jacobi矩阵的特征根分别为此时，当α/γ＜1时，λ1、λ2、λ3不全为负，Q8点是不稳定奇点；当时点为稳定结点.

结合以上分析，对于系统（5）可以得出如下引理.

（2）当α/γ＞1时，Q8点为稳定结点，Q2、Q3、Q4点是不稳定奇点.

此时对系统（5）进行数值仿真其相图如图3所示.系统（5）在不同条件下的竞争过程如图4所示.

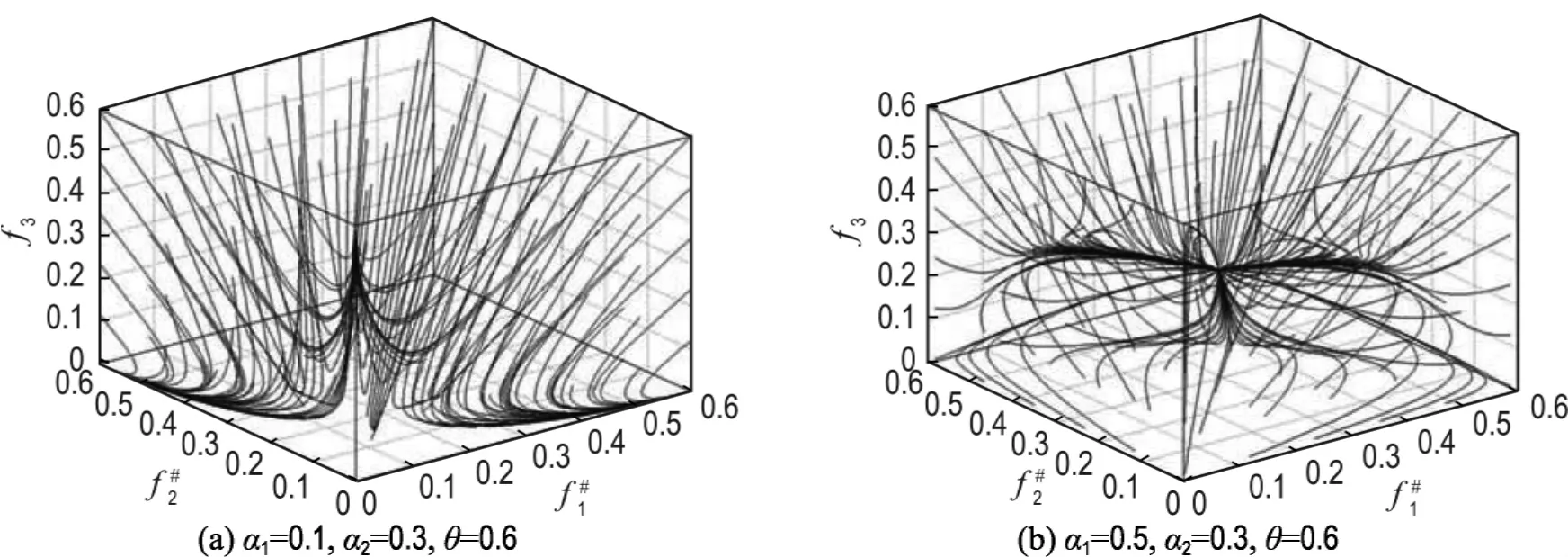
图3 系统（5）的相图Fig.3 Phase diagram of System （5）

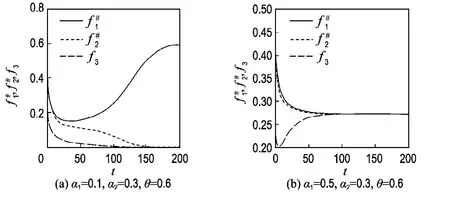
图4 系统（5）的网站竞争过程示意图Fig.4 Schematic of competitive processes between websites of System （5）

2.3 整体市场中的情形

与文献［2、8］类似，给出如下定义：

定义1 如果0＜α/γ＜1，则称系统（6）中的各网站之间属强竞争；如果α/γ＞1，则称系统（6）中的各网站之间属弱竞争.

由于当i∈ ［1，r］时θfi，根据引理1、2可得下面定理.

定理1 在第一象限，三网站市场细分的网站竞争模型稳定的平衡点有5个.令，则这5个平衡点分别是

（2）当α/γ＞1时，O1点为稳定结点，O2、O3、O4、O5点是不稳定奇点.

此时对系统（6）进行数值仿真其相图如图5所示.系统（6）在不同条件下的竞争过程如图6所示.

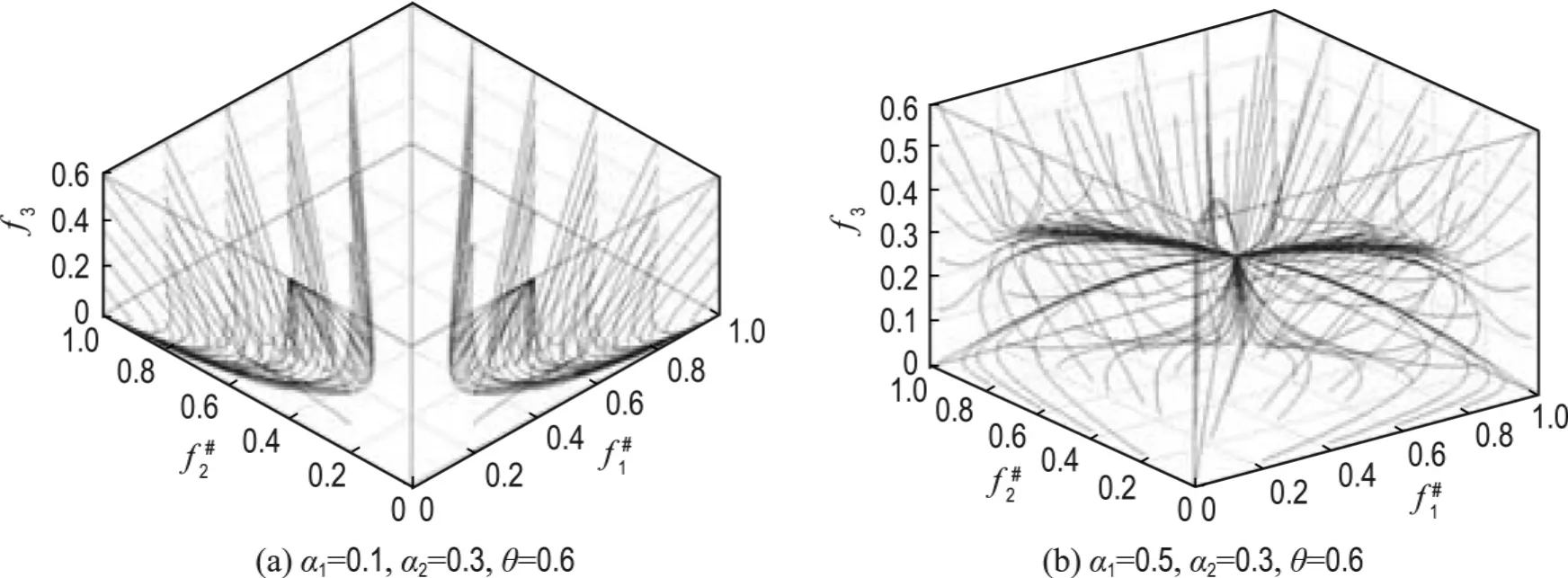
图5 系统（6）的相图Fig.5 Phase diagram of System （6）

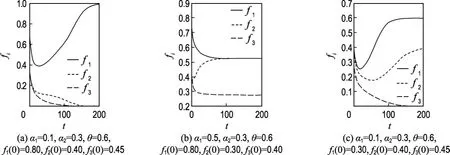
图6 系统（6）的网站竞争过程示意图Fig.6 Schematic of competitive processes between websites of System （6）

3 参数分析

由上述分析可知，系统（6）在参数取值发生变化时均衡状态会随之发生改变.在基于Lotka－Valterra系统的网站竞争模型所描述的三网站竞争系统中，如果网站间的竞争非常的激烈，则访问了一个网站的用户将不再去访问其他的网站，由文献［3］知，对于基于Lotka－Valterra系统的网站竞争模型而言，激烈的市场竞争直接导致初始市场占有率高的站点成为霸主，而其他站点消亡.而由定理1知，在本文所描述的市场细分的网站竞争模型中，情况则有所不同.

当市场中各网站之间的竞争关系属弱竞争时，系统中各网站可以共存，但因为在θ的取值范围内均有因此未进行市场细分的网站最终保有较高的市场占有率，此时，对于参与市场竞争的网站来说，进行市场细分就不是最优的选择了.在互联网发展初期，一些综合性的门户网站占据着主要的市场份额恰好成了这一结论的佐证.

当市场中各网站之间存在强竞争关系时，网站竞争的结果不再是单纯的趋于O2或O3点，而是呈现“赢家通吃”的局面，通过进行适当的市场细分并且初始市场占有率满足时，竞争结果有可能趋于O4或O5点，从而弱者有可能在激烈的竞争中生存下来；而当θ＞0.5时，弱者专注于细分市场甚至会在竞争中胜出.这一结论很好地解释了在网络经济日趋成熟的今天，诸如优酷、泡泡网、淘宝、阿里巴巴等专注于某一细分市场的网站纷纷崛起，新的综合性门户网站却鲜有出现的现象.

4 结 语

在本文所建立的存在细分市场的网站竞争模型中，如果网站间的竞争关系属于弱竞争，未进行市场细分的网站最终保有高市场份额，从而在竞争中处于优势地位.如果市场中各网站之间存在强竞争关系，弱者有可能通过适当地对目标市场进行细分而在激烈的市场竞争中生存下来，避免整个市场呈现“赢家通吃”的局面.如果弱者锁定的细分市场潜力巨大，则弱势网站甚至可能后来居上在竞争中胜出.

本文及以往的网站竞争模型均假设网站推广过程类似于生物学中的种群增长及病毒扩散，即网站推广策略为病毒营销模式，而实际情况并不完全如此.很多运营商在进行网站推广的时候，综合运用了传统推广模式和病毒营销模式，显然研究这一类网站相互竞争的情况是很有意义的工作，有待于进一步拓展.另外，以往模型均假设忽略推广成本，假设网站在竞争中以追求市场份额最大化为目标，而阿里巴巴一度陷入困境正是因为忽略了推广可能付出的巨大成本而一味地追求大的市场份额，因此，对于网站竞争过程的成本与效益进行分析也是有待于进一步研究的内容.

［1］MAURER S M，HUBERMAN B A.Competitive dynamics of web sites ［J］.Journal of Economic Dynamics and Control，2003，27（11－12）：2195－2206

［2］LPEZ L，SANJUAN M A F.Defining strategies to win in the Internet market［J］.Physica A：Statistical Mechanics and Its Applications，2001，301（1－4）：512－534

［3］WANG Yuan－shi， WU Hong. Dynamics of a cooperation－competition model for the WWW market［J］. Physica A：Statistical Mechanics and Its Applications，2004，339（3－4）：609－620

［4］JIANG Ji－fa， CHENG Zhi－xin. The complete strategic classification for a cooperation－competition model in the WWW market［J］.Physica A：Statistical Mechanics and Its Applications，2006，363（2）：527－536

［5］XIAO M，CAO J.Stability and Hopf bifurcation in a delayed competitive web sites model ［J］.Physics Letters A，2006，353（2－3）：138－150

［6］LI Y H，ZHU S M.Competitive dynamics of e－commerce web sites ［J］. Applied Mathematical Modelling，2007，31（5）：912－919

［7］李艳会，朱思铭 .一类电子商务网站竞争模型分析［J］.中山大学学报，2003，42（5）：6－10

［8］吴 红，王世远 .网站竞争模型的定性分析 ［J］.控制理论与应用，2005，22（2）：218－222