六角形目经编网片和菱形目有结绞捻网片水动力性能比较研究

2010-06-13许永久黄洪亮冯春雷周爱忠

浙江海洋大学学报(自然科学版) 2010年4期

许永久，黄洪亮，王磊，冯春雷，张勋，周爱忠，张禹

（中国水产科学研究院东海水产研究所，农业部海洋与河口渔业重点开放实验室，上海 200090）

海水养殖网箱是我国近年来发展较快的渔业设施，随着网箱的养殖已逐步推向海况条件更为复杂的湾外半开放或开放海域，对网衣材料性能和网片的结构提出了更高的要求[1-4]。目前，国内外对网箱网片的研究多集中于网片的力学性能和数学模拟研究[1-7]，有关六角形目和菱形目等不同结构网片之间的比较研究已有部分作者报道，但主要偏重于其材料性能和拉伸力学性能[8-10]，对于六角形网目网片的水动力学性能的研究，宋伟华等[3]对其进行过理论分析，未从试验角度去验证。李玉成、詹杰民等[11，12]通过模型试验对有结、无结网片的水阻力系数进行比较分析，对不同结构网片之间的分析较少涉及。本文通过网箱网片模型试验，研究2种规格网片在不同水平缩结、不同流速下的阻力性能和水平与垂直运动变化，以期为网箱设计和渔用网片的选配提供数据参考，同时，本试验通过对六角形目网片网目尺寸探讨和试验分析，为六角形目网片的设计和计算提供理论参考。

1 材料与方法

1.1 试验设备

网片模型试验在东海水产研究所网具模型试验水池进行。试验静水池主尺度：90 m（长）×6 m（宽）×3 m（深），拖车车速范围0～4.0 m/s时，相对精度P≤1%，测力系统使用Lu-A型测力传感器，量程1 000 N；测力仪器的线性误差小于满量程的0.05%。

1.2 试验网片及装配

试验网片为规格1.7 m×1.7 m的方形网片，平面框架为1.7 m×1.7 m的可拆卸的刚性框架，其模型按相关标准制作[13]，具体参数见表1。网片框架，固定于方形浮体上，浮体前端连接测力传感器由拖车牵引。网片固定：根据缩结系数，网片四周固定在1.7 m×1.7 m的刚性框架上，网片框架由浮体4个角的绳索系紧固定。网片不固定：根据缩结系数，网片上部固定在1.7 m×1.7 m刚性框架上部，网片底端框架保留作重力牵引，两端框架均移出。框架具体装配如图1所示。

图1 网片框架装配图Fig.1 The layout of the frame system for the plane net

表1 实物网片及模型网片的主参数Tab.1 The main characteristics of full scale trawl nets and model trawl nets

1.3 试验方法

本试验采用《拖网模型试验水池试验方法》：渔具模型试验准则1（田内准则）进行[14]。模型大尺度比（λ）和小尺度比（λ′）均为 1。

1.3.1 网片阻力的测定和计算

模型网片和框架阻力通过测力传感器直接读取，并经过2个传感器数据处理后得到迎流方向总阻力，在同样速度下测得框架阻力，即得网片阻力=框架网总阻力-框架阻力，由于模型网（Fm）与实物网（Fs）大小尺度比均为1，Fm=Fs。在0.5～2 kn的相对流速范围内,对2种规格的模型网片进行阻力和水平、垂直运动变化试验。由于在静水池中采用拖动模型网片的办法来进行试验,故拖车的拖速作为水流速度。

1.3.2 2 种结构网片试验

试验选用六角形网目、菱形目有结绞捻网目2种网片，试验依次编号为N（0）、N（1）、N（2），网片的状态分为固定N（G）、不固定N（BG）。试验组合如下：

N（0）—N（G，BG）：为无网状态，平面框架固定与不固定试验；

N（1）—N（G，BG）：为六角形网目网片，a=16.7mm，缩结系数分别为 0.65、0.707、0.60；

N（2）—N（G，BG）：为菱形目有结绞捻网目网片，a=26mm，缩结系数分别为 0.65、0.707、0.60。

水平位移（Horizontal displacement，L）：运动过程中，网片底部与前部的水平间距（图2）。

与水平面垂直距离（H1）：运动过程中网片底部与水平面之间的垂直距离（图2）。

垂直位移（Vertical displacement，H2）：运动中网片底部位置与静止时网片底部位置的垂直间距（图2）。

六角形结构网目尺寸的计算：根据网目尺寸计算标准，按相邻3个六角形网目拉紧长度（包括3个连接边长，可视为菱形目结构的结节）的1/3测量结果可以看出（图3），六角形结构网目尺寸实际为4a，是菱形目的2倍。H1为与水平面垂直距离，H2为垂直位移，L为水平位移。

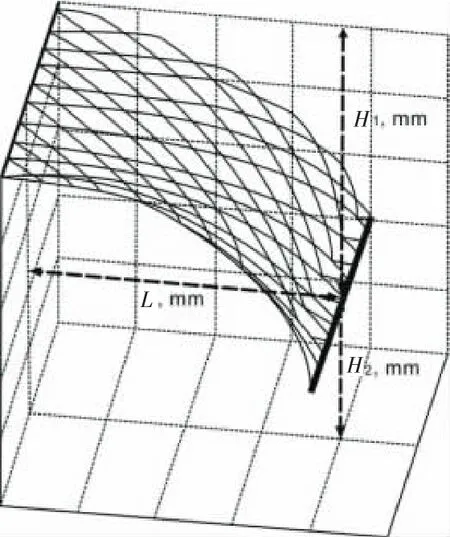
图2 网片的水平和垂直位移变化Fig.2 The variation of HD and VD

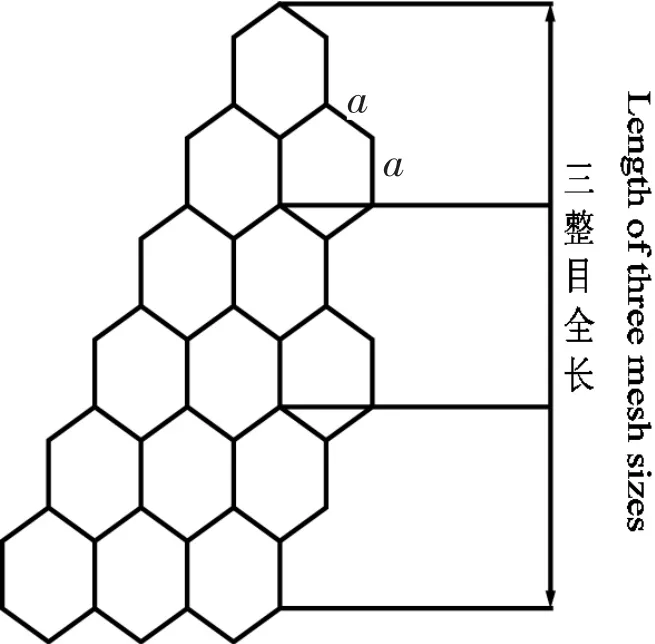
图3 六角形网目尺寸计算示意Fig.3 Sketch map of hexagonal mesh size calculation

2 结果与分析

2.1 相同规格网片不同水平缩结系数下流速与阻力之间关系

如图1所示，网片固定时，在不同水平缩结系数（0.65、0.707、0.6）条件下的阻力均随流速的增加而增加，其中六角形网目网片在水平缩结系数0.65时，阻力最低，水平缩结系数为0.6时，阻力次之，当缩结系数为0.707时，网片的阻力最大。有结绞捻菱形网目网片，在较低流速时（V＜1.5 kn），水平缩结系数为0.60时阻力最小，0.65时阻力最大。较高流速下（V＞1.5 kn），水平缩结系数0.60时阻力最大，0.707时阻力最小。菱形目有结网片试验结果，在水平缩结系数范围内（0.60～0.707），随着缩结系数的增加，网片阻力有减小趋势，与网片的线面积有关。根据相关理论计算可以得到，菱形目有结网片，在Et=0.707时，线面积最少，阻力组小。这与我国学者钟若英和周应祺等[17，18]结论相似。六角形目网片线面积根据计算，得到Et=0.707时最小，Et=0.60时最大。而试验中六角形目网片阻力变化却与此趋势相反，可能与其特殊的网目结构有关，也可能为网片的线面积随缩结系数差异太小，致使引起的阻力值变化。六角形目网片在0.5 kn流速时的网片最大阻力差值为10.192 N，2.0 kn时最大阻力差值为18.718 N，两者的变化率为83.7%。固定时的网片阻力变化说明在水平缩结系数（0.60～0.707）范围内，网片的有效投影面积变化不大。网片不固定时，在水流作用下产生垂直水平位移，受流线面积减小，平均阻力比固定时阻力小很多。从图1中（c，d）可以看出，随着流速的变化，受缩结影响，网片阻力差值变化也逐渐增大。由于网片不固定，缩结系数不仅对线面积产生影响，而且由于网片的密实度变化会引起网片漂流倾角变化。从而造成迎流面积发上变化，影响网片的阻力。

2.2 相同缩结系数下不同结构网片流速与阻力关系

固定网片阻力在V＞1.0 kn时普遍高于不固定网片，在较低流速下（V＜0.5 kn），固定网片与不固定网片阻力相差不大（图 2）。图 2（a，b，c）所示，网片固定时，2种网片之间的阻力差值随流速有增加的趋势。根据菱形网片线面积计算公式[17]：SX=4 ad×TtNn，计算网片线面积。Et为0.65、0.707、0.60时，有结绞捻目网片的线面积分别为0.468 3 m2、0.462 1 m2、0.482 2 m2（考虑结节影响，结节dk/d=3）。六角形目网片的线面积按照定义结合上述网目尺寸计算方法，Et为0.65、0.707、0.60时，分别为0.604 7 m2、0.573 6 m2、0.640 9 m2（六角形目网片由于其结构特殊，其网目尺寸无计算标准，本方法考虑其为正六角形，具体在讨论中进行了分析）。根据网片阻力计算公式R=Cx×ρSV2，网片阻力与其线面积有关。六角形目网片线面积较大，阻力因而较大，与试验结果吻合。六角形目网片的尺寸（a=16.7 mm）较小，比菱形目网片（a=25）小40%，是其线面积较大，阻力大原因之一。另外，六角形目网片垂直边为双线结构，是其线面积增加的又一原因。

不固定网片在低流速下（V＜1.5 kn），网片阻力变化趋势与固定网片相同，六角形目网片阻力较大，无结菱形目网片阻力较小。流速V＞1.5 kn时，菱形目有结绞捻网片阻力较大，六角形目网片阻力较小。由于不固定网片的阻力受流速、结构变化影响较大，试验中，网片形成倾角和拱度，线面积等计算较为复杂。因此其阻力之间的比较仍需要更进一步试验分析。

2.3 网片的水平位移与垂直位移运动变化

2.3.1 相同网片不同缩结系数下水平和垂直位移变化

网箱网片的水平垂直运动，关系到其在水中的变形，网片不固定时，下加框架，牵引网片运动。试验中，最小流速时（0.5 kn），网片变形不大，形成网片曲面也不明显。此时在忽略网片拱度条件下，网片的斜边长度X可视为网片起初静止时距水平面距离，得。垂直位移H2=X-H1。图6为2种网片在不同水平缩结下水平垂直位移随流速的变化关系，水平垂直位移与流速成指数关系。可以看出，相同网片水平和垂直位移受缩结影响较小，说明不同缩结系数对于网片的变形影响较小。水平垂直位移均随着流速的增加而增大。相同流速下，水平位移的变化比垂直位移变化大。主要由于起始时，水平方向上影起阻力大于网片向上运动的力，图 6（a，b，c）中可以看出，六角形目网片和有结绞捻网片，在Et=0.707时水平位移均最小，在Et=0.60时最大。这种变化趋势与其受到的阻力有很大影响。垂直位移的变化规律与水平位移相似，2种结构网片在Et=0.60时，垂直位移均最大，在Et=0.707，0.65时，垂直位移较小。最后比较认为，相同网片的水平位移与缩结关系不明显。垂直位移在缩结范围内（0.60～0.707）随着缩结减小有逐渐增大的趋势。

图4 网片固定时阻力与流速关系（固定与不固定）Fig.4 Relationship between fishing net resistance and velocity of flow during fixation or not

图5 相同缩结网片阻力与流速关系Fig.5 Relationship between fishing net resistance and velocity of flow during the same Et

2.3.2 相同缩结系数不同网片水平和垂直位移变化

网片的结构差异引起其阻力变化，也相应的影响其运动变化。相同缩结系数下网片水平和垂直位移随流速的变化关系如图7所示，比较发现，六角形目网片水平和垂直位移在不同缩结下均较大，有结绞捻网片水平和垂直位移均较小。图 7（a，b，c）所示，六角形目网片水平位移比有结绞捻平均大32.6%，垂直位移大31.8%。而在Et为0.65、0.707、0.60时六角形目网片比有结绞捻网片分别大29.1%、24.1%、32.9%。六角形目网片水平垂直位移最大与其线面积有关，由于网片在水中的受流面积变化影响网片的阻力和流态的变化，线面积越大，其受流面积越大，受到的作用力也越大。通过比较发现，网片阻力引起的位移变化占显著作用，但其他因素也对运动变化有影响，如流态的影响等。有结绞捻网片线面积计算值偏大，说明其结节的用线量考虑过多，其结节在水中所受的作用力有限。

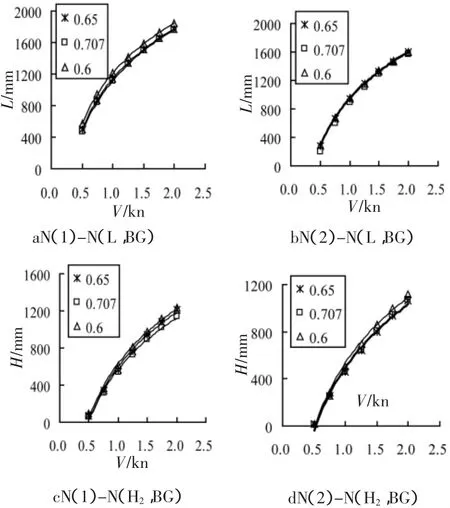
图6 不同缩结系数下流速与水平和垂直位移关系Fig.6 Relationship between displacement variation andvelocity of flow in different Et

图7 不同网片流速与水平和垂直位移关系Fig.7 Relationship between displacement variation and velocity of flow during the same Et

3 讨论

3.1 六角形目网片的缩结和网片线面积计算

六角形目网片网目尺寸和缩结的研究国内较少报道，仅见国外有相关研究，本次实验选用六角形结构主要考虑其在国内网箱和远洋拖网渔业中有较多应用[3，15]。传统观点认为，六角形目网片在作业中可降低渔具阻力，增大拖网速度，在网箱中，使用六角形目网片可使网箱的容积变化率较小，网箱易于移动[16]。六角形网片缩结系数根据定义计算，假设试验中六角形为正六角形。其缩结系数按照有关文献[3，17，18]计算可得，六角形目网片水平缩结系数Et分别为0.65、0.707、0.60时，En为0.88、0.853 5、0.90。线面积计算如图3所示，将六角形目网片垂直边视为菱形的结节，然后按传统方法进行线面积计算（由于垂直边为双线，每个网目计算线面积时，增加一个垂直边的线面积）。得到其Et为0.65、0.707、0.60时线面积分别为0.604 7 m2、0.573 6 m2、0.640 9 m2。同理，有结绞捻目网片在 Et为 0.65、0.707、0.60 时的线面积为 0.468 3 m2、0.462 1 m2、0.482 2 m2。2种网片的线面积计算时，考虑网线的粗度平均（d=2 mm），六角形为正六角形，有结绞捻网片结节直径dk与网线线径d关系为dk/d=3[17，18]。

3.2 水平缩结系数差异对网片阻力及运动的影响

相同网片，不同缩结系数之间的差异对网片的阻力性能和运动有影响，根据有关结论，菱形网片在水平缩结系数为0.707时，网片的利用率最大，用线量最小[17]。有结菱形绞捻网片阻力，在缩结0.707时，阻力最小，而在稍小的缩结下（0.65，0.60）阻力较大，与此观点相符。试验选取的缩结系数均在最佳缩结之内。随着缩结系数的增加，网片的用线量逐渐减少，阻力降低。在缩结为0.65～0.707之间时，网片的用线量和线面积差异不明显。这也说明在越接近最佳缩结时，网片的阻力和运动变化越相近。根据有关研究[3]，六角形目网片在Et=0.866时，网片的用线量最小，与菱形目网片相同，在缩结越接近0.866时，网片的用线量越小，阻力越小。试验中，六角形网片阻力值随缩结的这种变化趋势正好相反，可能因为六角形网目尺寸较小，以及六角形直边使用双线，网线粗度（d）增加，使得d，a等因素在阻力中的影响增加。也可能是缩结系数之间的线面积的差异不明显，造成了阻力结果较为接近。图3-a中也可看出，缩结0.707与0.60几乎接近。

根据我国有关学者的聚乙烯网片阻力计算公式[18]：R90=k×SsV1.8(R90-网片与水流垂直时阻力kg；Ss-网片线面积；k-阻力系数，取最大值58.2)，试验中，有结菱形目网片阻力与计算结果基本相符，相差不大。六角形目网片在Et=0.707时，阻力最大，与线面积公式计算结果不符，可能受网目结构的影响，具体原因有待更多试验分析。缩结系数差异对于水平垂直位移的影响不大，可能与缩结系数引起的阻力差异有关。由于网片不固定时的流态和运动较复杂，缩结的变化对其影响有待后续研究。

3.3 网片的差异对于网片阻力和运动变化的影响

六角形目网片，缩结在Et=0.866时，网片的缩结面积最大，利用率最高，与菱形网片最佳缩结0.707存在差异，其值比菱形网片最佳缩结系数0.707大，当菱形网片最佳缩结时，用线量最少，六角形网片用线量未达到最少。由平面网片的一般公式可知，网片阻力与线面积及网目尺寸相关，六角形目网片线面积较大，阻力最大，与试验结果趋势吻合。而有结绞捻网片的计算阻力比试验阻力稍大（平均计算阻力/试验测试阻力=1.08），原因主要是与有结绞捻网片网线光滑，在试验过程中与水摩擦力较小，而六角形经编网片其网线表面粗糙带毛边，与水摩擦力，造成了试验阻力较大，而实际计算时，并没有考虑这些因素。另外，理论计算考虑结节直径过大，也是造成有结绞捻网片计算线面积过大的原因。网片的运动变化随网片结构差异而变化，因为受阻力的影响，网片的水平垂直位移发上相应的变化。阻力对于运动变化起显著作用，但试验结果比较发现，其他因素如流态等也对网片运动变化产生影响。

3.4 网片的阻力性能以及设计分析

深水网箱中，网衣（网片）是主要受力部分，根据相关研究，整体网片阻力占整个网箱箱体阻力的88.9%[19，20]。改善网片网衣的性能对于提高整个箱体的性能有明显的益处。经编网片是网箱中广泛使用的网具材料[21，22]，主要为避免网片结节对鱼体表面伤害的影响。而在试验中，有结绞捻的阻力性能和运动变化均优于六角形经编网片，与绞捻网片的网线光滑，水摩擦力较小有关。六角形目网片的结构与菱形不同，从试验结果发现，六角形目网片在相同缩结时，阻力更大，与传统观点认为六角形目网片节省阻力略有差异。说明网线粗度d和网目结构对阻力的影响要大于缩结对阻力的影响，具体需要进一步的试验分析。

[1]袁军亭.网片的三维力学模型研究及应用[D].上海：上海水产大学,2007：8-17.

[2]宋伟华,杨永位.六角形目孔片的研究[J].水产科技情报,1999,26（6）：248-251.

[3]FREDRIKSSON D W,SWIFT M R，IRISH J D，et al.Fish cage and mooring system dynamics using physical and numerical models with field measurements[J].Aquacultural Engineering,2003,27：117-146.

[4]BALDWIN K，CELIKKOL B，STEEN R，et al.Open aquaculture engineering:mooring and net pen deployment[J].Mar Technol Soc J,2000,34(1)：53-67.

[5]王飞,丁天明.圆柱形网箱锚绳受力特性的数值模拟[J].海洋水产研究,2007,28（2）：36-44.

[6]COLBOURNE D B，ALLEN J H.Observations on motions and loads in aquaculture cages from full scale and model scale measurements[J].Aquacult Engineering,2001,24(2)：129-148.

[7]FREDRIKSSON D W.Open ocean fish cage and mooring system dynamics[D].Durham,NH:The University of New Hampshire,2001.

[8]石建高,王鲁民,徐卓君.高强度聚乙烯菱形网目经编网片的力学性能初步研究[J].中国海洋大学学报：自然科学版,2006,36（3）：410-414.

[9]石建高,王鲁民.渔用高强度聚乙烯和普通聚乙烯六角形经编网片的拉伸力学性能比较研究[J].海洋水产研究,2007,28（6）：72-76.

[10]张立英,侯恩淮,张春桂.用计算机计算拖网网片的剪裁与吃扣缝合[J].中国水产科学,1994,1(1)：61-64.

[11]李玉成,桂福坤,张怀慧,等.深水养殖网箱试验中网衣相似准则的应用[J].中国水产科学,2005,12(2)：179-186.

[12]詹杰民,胡由展,赵陶,等.渔网水动力试验研究及分析[J].海洋工程,2002,20(2)：49-59.

[13]SC/T 4014-1995拖网模型制作方法[S].北京：中国标准出版社,1995.

[14]SC/T 4011-1995拖网模型水池试验方法[S].北京：中国标准出版社,1995.

[15]许永久,张敏,邹晓荣,等.我国智利竹筴鱼中层拖网网具性能研究[J].上海水产大学学报,2008,17(2)：215-221.

[16]王鲁民,黄洪亮,王明彦,圆形重力式网箱阻力性能研究[J].中国海洋大学学报:自然科学版,2006,34（4）：555-559.

[17]钟若英,赵瑞生,王维权.渔具材料与工艺学[M].北京：中国农业出版社,1996：177-189.

[18]周应祺,许柳雄,何其渝.渔具力学[M].北京：中国农业出版社,2004：51-71.