全数字接收机中基于准自适应短时反馈的残余频偏纠正算法
2010-06-11孙文胜徐福新
孙文胜,刘 婷,徐福新
(杭州电子科技大学通信工程学院 杭州 310018)
1 引言
20世纪80年代中后期,一种新的接收机概念——全数字接收机[1~3]出现在人们的视野中。与传统的无线电数字通信接收机不同,全数字接收机在数字通信接收机的模拟处理区引入了数字处理技术。在全数字接收机中,数字下变频的本地振荡信号是一个固定频率的自由振荡信号,它不可能和输入信号的载波频率完全相等,它们之间必然存在频差,为了实现载波同步,必须估计和消除频偏误差。传统的数字通信系统通常采用锁相环实现载波同步[4],受无线传输及相关器件的影响,用锁相环锁定载波相位和时钟相位并非真正的无偏估计;而全数字接收机采用高速信号处理技术,可以更加精确地估计并纠正频偏。
全数字接收机的开环频率估计算法主要有数据辅助和非数据辅助两种,从试验结果来看,这些频偏算法虽然大大降低了系统的频偏,但是没有完全解决频偏估计问题,仍然有剩余频偏无法得到纠正。由于这些残余频偏对系统造成的误码率影响很大,因此对残余频偏的纠正是一个不能忽略的问题。参考文献[5]提出利用数据帧内各个OFDM符号的循环前缀分别进行残余频偏纠正的算法,该算法虽然能够较好地纠正每个OFDM符号内的残余频偏,但是复杂度较高,在实际应用中较难实现。参考文献[6]提出利用象限旋转、坐标平移等操作从数据符号中提取相位信息来纠正残余频偏,其计算涉及符号取反、虚实交换、累加等,且仅适用于多径衰落信道。参考文献[7]提出基于NDA采用PLL的判决反馈结构对残余频偏进行估计补偿,但采用基于判决的反馈结构可能会带来错误传播,恶化接收机性能。本文提出的纠正残余频偏算法采用均方误差值作为衡量标准,通过调节步长来改善残余频偏,计算方法简单,硬件容易实现,仿真结果显示性能良好。
2 残余频偏
在全数字接收机中,设ck为发送的数据信号序列,Δω为载波频偏,θ为载波初始相偏,n(k)~N(0,2σ2)为方差是σ2的加性高斯白噪声,r(k)表示经定时恢复后的数据信号,则在定时恢复理想的条件下满足以下条件。
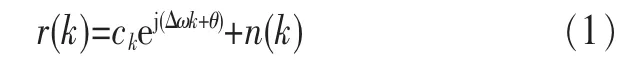
在实际中,受所采用的频偏估计算法的精度和噪声等因素的影响,由频偏估计算法计算得到的载波频偏Δω并不等于真实存在的频偏值,即接收信号经过频偏纠正后仍存在剩余频偏,此时实际的数据信号可表示如下。
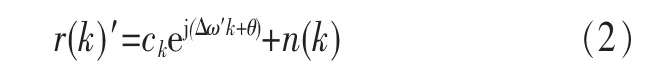
式中,Δω′代替了原来的Δω,表示纠正后的残余频偏。
接收机的载波同步问题包括频偏纠正和相位补偿两方面,一般来说,相位补偿的前提是频偏得到了很好地估计和校正,但在残余频偏的影响下,实际的相位补偿应表示为:

将式(2)代入式(3)运算后得到:
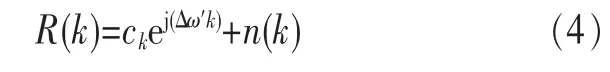
从式(4)可以看出,残余频偏经过一段时间跨度后会转化为残余相位,用φk表示残余相位,n(k)为相位噪声,则有:

由于载波频偏没有得到很好的纠正,因此这种附加相位偏移不能用统计相位估计方法纠正。这些相位噪声会导致星座图模糊,影响系统的误码率性能。尤其在256QAM这样的信号情况下,由于星座图上的信号点分布密集,因此残余频偏转换对相位噪声的影响非常严重。
表1给出了在不同信噪比、初始频偏不同的条件下,Kay估计器[8~9]的残余频偏Δf及误码率Pe(设实验100次,估计结果取100次实验结果的均值)。表1中ΔF为Kay估计校正前频偏,SNR为信噪比,Δf为Kay估计校正后的残余频偏。从表1中可以看出,即使在高信噪比条件下,仍然存在几Hz的残余频偏,其导致了解码性能的下降。
3 均方误差准自适应短时反馈算法
为了校正残余频偏,并且考虑到无线信道通常在缓慢地变化,本文提出了一种均方误差准自适应短时反馈算法。这里的反馈与锁相环的反馈不同,它是根据设定的均方误差门限,用快速迭代法求出残余频偏,并以此值为基准对随后的信号进行纠正,因求得的均方误差时间及迭代时间极短,所以我们称之为“短时反馈”;均方误差的取样数和取值间隔取经验值,它们的取值对结果不会造成决定性的影响,这种方法我们称之为“准自适应法”。在时间间隔到来之时,首先取样进行运算,运算过程中信号的纠正按规定的步长值进行,运算后得到最新的残余频偏,后续的信号按此纠正,即后续的步长值取前一次纠正后计算出的残余频偏值。如此反复,既保证了在信道变化时能即时计算出残余频偏的大小,也让计算简单化,并且不用考虑时延的影响。下面详细介绍这种算法。
数字化了的接收机基带信号,通过载波频差纠正、载波相位误差纠正和时钟误差纠正后,符号输出为{Ii(t),Qi(t)},如果{Ii(t),Qi(t)}对应星座图上的坐标点与星座图上的标准信号点{aj,bj}距离最近,在数字通信中通常将{Ii(t),Qi(t)}判决为信号{aj,bj}。定义接收机N(N是个经验值)个信号的均方误差为σ,σ的取值如下。
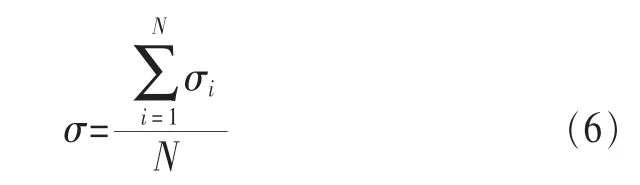
式(6)中的 σi由式(7)得到:
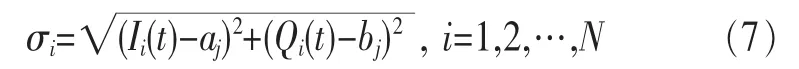
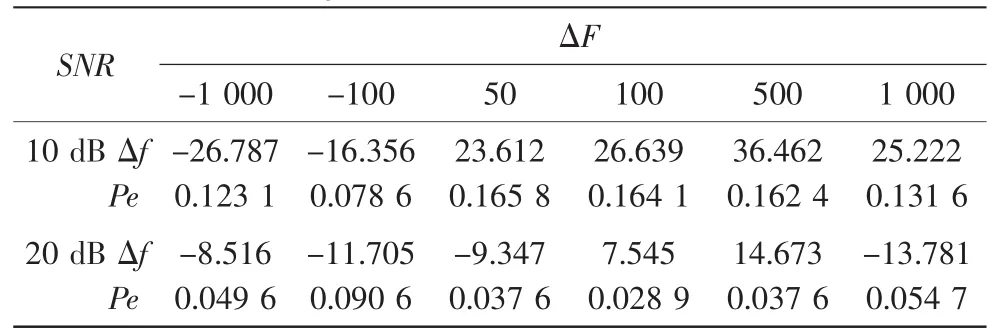
表1 Kay估计器的残余频偏及误码率
式(7)实质上是把解调后的信号点在星座图上的位置与最近信号点(i、j不一定相同)的位置进行比较,记录它们之间的距离差。连续N个信号点都进行这样的误差统计,然后按照式(6)求距离差的均方误差。根据实际要求的误码率,规定一个误差门限值(取经验值),当σ大于此值时,就表示{Ii(t),Qi(t)}距离参考信号点{aj,bj}较远,误码率达不到要求,需要采用本算法进行纠正。
由于在接收机前采用了类似Kay估计器的频偏估计算法,因此得到的频偏值比较接近真实值,此时残余频偏是小频偏,这个残余频偏值可能为正,也可能为负。在这种情况下,可以采取逐次逼近的方法进行频偏纠正。现将算法步骤介绍如下。
①根据式(7)计算当前均方误差σ。
②规定一个合适的步长L。第一次纠正L Hz,L取经验值。由表1可知:原始频偏越大,残余频偏越大;信噪比越小,残余频偏越大。因此,可根据原始频偏及信噪比确定适合的步长。这里需要说明的是,L的大小并不影响算法的结果,仅影响迭代次数,在完成第一次残余频偏纠正后,可将上次纠正的残余频偏值作为下次的步长L。
③设本次纠正后的均方误差为σ′,前一次纠正后的均方误差为σ。首先纠正L Hz,计算σ′,把它与σ比较。如果σ′<σ,继续按此步长纠正并计算均方误差,直至 σ′>σ,此时改变步长值为-L/2 Hz,即缩小步长值为原来的1/2并向相反方向纠正频偏,相反方向纠正频偏至σ′>σ时,调整步长值为L/4,即步长值反向并缩小2倍,继续迭代并比较σ′与σ之值。如此反复至σ′的值小于规定的均方误差判决门限值即可。
④如果第一次纠正L Hz后σ′>σ,则说明纠正方向不对或者步长过大,此时直接将步长调整为-L/2进行纠正,其余操作如③。
此算法的关键在于不断比较后一次与前一次均方误差值,当后一次均方误差值比前一次小时按原来步长纠正频偏,当后一次均方误差值大于前一次时,纠正方向改变,纠正数值减小为原来的一半。通过不断迭代,残余频偏得以良好的消除。把每次反馈进行频偏纠正的值累加起来就可以得到残余频偏值。
一般在信道不改变的情况下,残余频偏的变化是缓慢的,可以认为在一段时间内残余频偏值是不变的,所以一次残余频偏纠正具有一定时间的持续有效性。这就是说适当的纠正间隔也是必要的。虽然通过短时反馈能够较准确地计算出残余频偏,但是在对后续接收信号的纠正中如何判断纠正的有效时间以及如何利用均方误差阈限准确地判决残余频偏并进行计算显得非常关键。在实验中对均方误差阈限值进行研究,发现它受某些参数的影响。下面就MPSK和MQAM说明均方误差阈值实验取得的过程。
(1)MPSK解调码元周期与均方误差阈限的关系
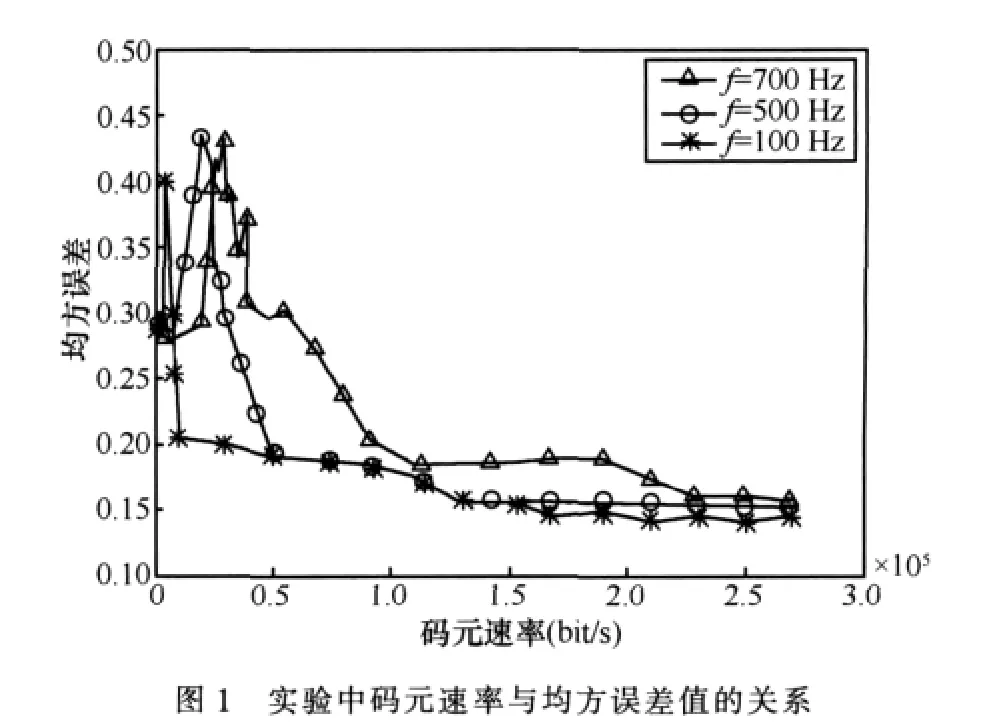
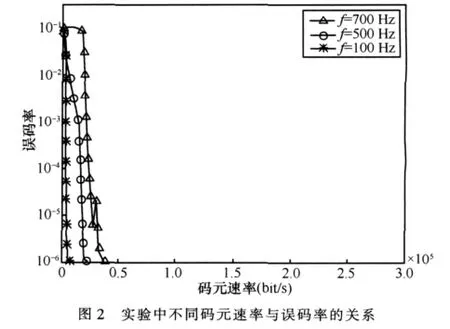
首先探究在MPSK解调中码元周期、预设频偏同均方误差之间的关系,这里以解调8PSK信号为例进行说明,并用码元速率来表达码元周期,码元速率与均方误差值的关系如图1所示,不同码元速率与误码率的关系如图2所示,三条曲线分别代表三种不同的预设频偏下的曲线。
在图1可以发现,当码元速率达到某一个固定值的时候,如果继续下降,均方误差值出现显著上升的趋势并随着码元速率减小到一个峰值然后骤然下降。当均方误差从峰值下降时,对应的图2的误码率仍然保持很快的增长趋势,甚至当均方误差值低于判决阈限时(如图1中表示的0.3),图2中的误码率攀升到接近于10-1。这个问题很重要,它关系到在什么情况下可以使用提出的均方误差短时反馈算法纠正残余频偏。
以8PSK为例,将解调后的点与8PSK星座图上8个标准点进行比较,并且计算解调后的点与标准星座图上点的距离差,将距离标准点最近的点判定为属于此标准点,正是因为这样,在偏差大时判定可能出错。如图3所示,解调后本应为A位置的点在不同频偏情况下分别偏移到了a、b、c,可以看出 a点与 A点的位置非常接近,根据式(6),当大部分解调后的点处于这种情况(其他标准点B、C、D、E、F、G、H同A点)时,生成的均方误差值一般低于判决阈限,此时可认为无需进行频偏调整。当偏移点为b时,如果解调后的点均为这种情况,显而易见均方误差值要高于判决阈限,这时候就要对其进行残余频偏纠正,使解调后的点最大程度地向A点靠近。但当点的位置偏移到c时,判决时与它对应的标准点为B,如果大部分解调后的点的情况如此,虽然系统的均方误差值会很小,但是误码率极高,这种情况无法利用均方误差短时反馈算法进行残余频偏纠正。
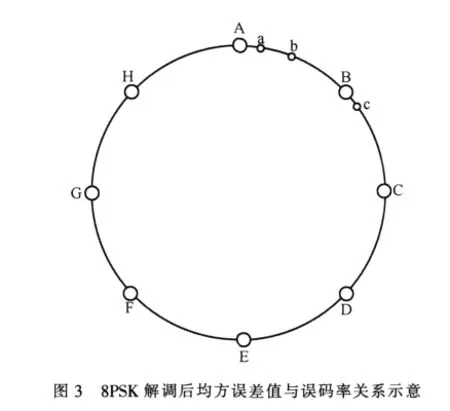
同时将图2中码元速率的临界值对应到图1中不难发现,对应系统要求的误码率可得到对应的均方误差值,此值即可作为均方误差阈限值。实验中预加的不同频偏值对应的曲线在近乎零误码率下的均方误差值的阈限是相同的,这说明系统中的频偏值不影响均方误差短时反馈算法中判决阈限值的设定。从图1中可以看出:当预设频偏为700 Hz时,判决阈限约为0.35;当预设频偏为500 Hz时,判决阈限约为0.35;当预设频偏为100 Hz时,判决阈限仍约为0.35。
(2)MQAM解调M值与均方误差阈限的关系
在MQAM中不同的M值所对应的零误码率下的均方误差阈限随着M值的变化而变化。假设已调制的信号最大幅度为1,则MQAM为矩形的最小码距为:
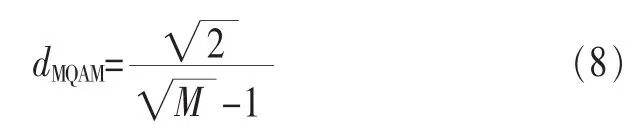
式(8)说明,随着M值的增大,各标准点之间的最小码距是逐渐递减的,也就是说M值越大,其抗干扰能力越差。如图4所示,未纠正残余频偏前,很小的残余频偏也会导致256QAM的星座图十分模糊。
由于高阶的MQAM系统其码距很小,因此算法所要求的均方误差阈值也应相应减小。实验得出在MQAM中M值与均方误差阈值的关系如图5所示,可以看出在MQAM中零误码率的均方误差阈值是随着M值的增加而减小的。
图6给出了256QAM残余频偏调整之后的星座图,与图4对比可明显看出去除残余频偏的256QAM星座图比有残余频偏的256QAM星座图清晰,也就是说去除残余频偏后得到的码元误码率明显降低。
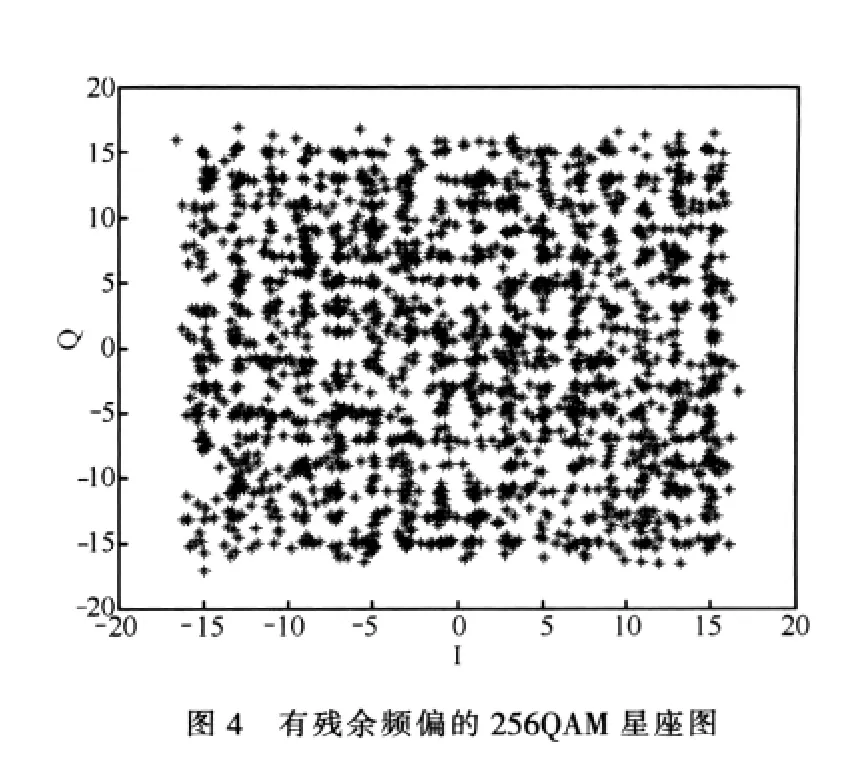
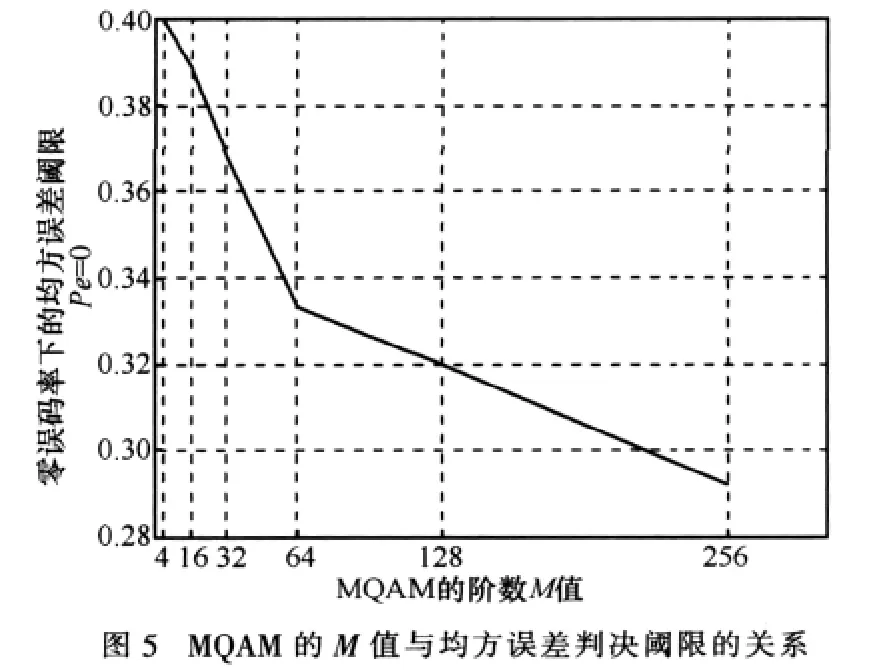
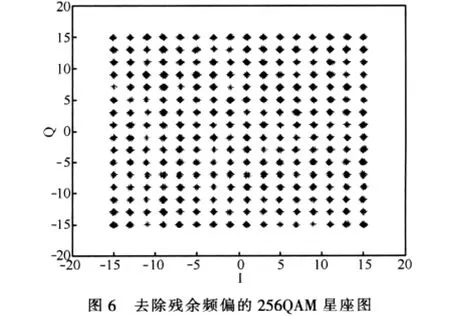
表2给出了利用均方误差反馈算法经多次实验后得到256QAM系统的误码率等相关实验数据。
需要注意的是,本文提出的这种残余频偏纠正算法不能独立地成为一种频偏算法解决方式,它的应用必须建立在系统已经通过较为有效的频偏估计算法对频偏进行纠正的基础上,只有这样才能对频偏进行更有效的纠正。
4 结语
本文提出了一种纠正残余频偏的均方误差反馈算法,并说明了均方误差阈值的选取方法。此算法以一定的运算量为代价,达到对残余频偏有效纠正的目的。Matlab仿真结果表明,利用此算法纠正残余频偏后系统误码率明显降低。
在实际应用中,可利用一个适当大小的存储器来存储每次经过频偏纠正后的数据,以备下次反馈之用。在信道条件相对稳定的情况下,残余频偏的变化是缓慢的,可以认为在一段时间内残余频偏的频偏值是固定的,这时利用已得到的残余频偏值直接对信号进行纠正,只需进行一两次迭代即可,也就是说在信道条件稳定的情况下,较小的计算量也能弥补系统误码率性能不足之处,满足实时处理的要求。
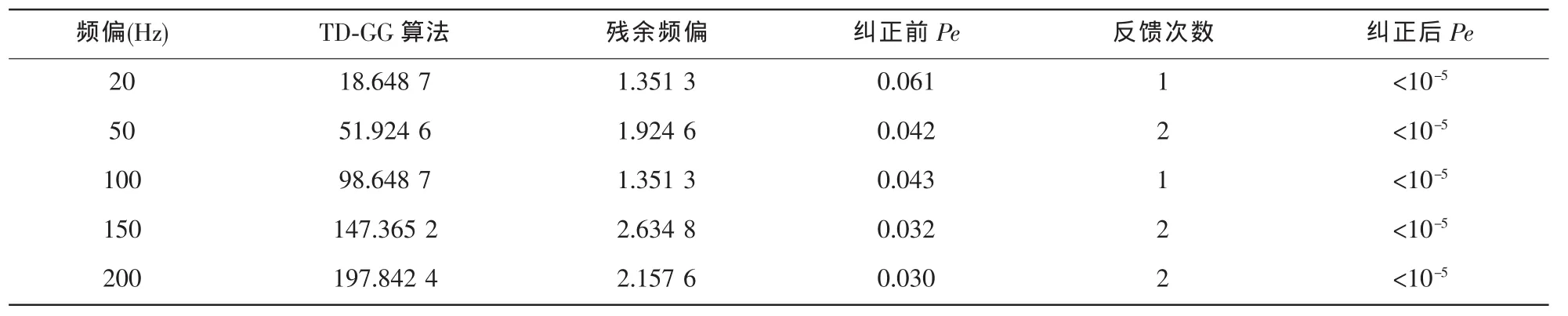
表2 256QAM均方误差反馈算法实验数据
1 张公礼.全数字接收机理论与技术.北京:科学出版社,2005
2 戈稳.雷达接收机技术.北京:电子工业出版社,2005
3 Tsui J著,杨小牛等译.宽带数字接收机.北京:电子工业出版社,2002
4 陈红.锁相环同步检波技术及在视频检波中的应用.现代电子技术,2008(15):184~192
5 彭小勇.一种新的基于循环前缀的残余频偏纠正算法.中国电子学会第十一届青年学术年会论文集,2005:215~219
6 李颖.相干QPSK/QAM OFDM系统中的残余频偏补偿算法.2005年通信理论与信号处理年会论文集,2005:275~281
7 Linling K.A time-frequency decision-feedback Loop for carrier frequency offset tracking in OFDM systems.IEEE Transactions on Wireless Communications,2005,4(2):367~373
8 Gini F,Giannnakis G B.Frequency offset and symbol timing recovery in flat-fading channels:a cyclostationary approach.IEEE Transactions on Communications,1998,46(3):400~411
9 Kay S.A fast and accurate single frequency estmator.IEEE Transactions On ASSP,1989,37(12):1987~1990
