直线一级倒立摆控制策略研究及仿真分析

梁春辉,冯 雷,张 欣

(长春工程学院电气与信息工程学院,长春130012)

0 引言

倒立摆系统是研究控制理论的一种典型的实验装置,具有成本低廉,结构简单,参数和结构易于调整的优点。然而倒立摆系统具有高阶次、不稳定、多变量、非线性和强耦合特性,是一个绝对不稳定系统。倒立摆实物仿真实验是控制领域中用来检验某种控制理论或方法的典型方案,它对一类不稳定系统的控制以及对深入理解反馈控制理论具有重要的意义。倒立摆系统在研究双足机器人直立行走、火箭发射过程的姿态调整和直升机飞行控制领域中有重要的现实意义,相关的科研成果已经应用到航天科技和机器人学等诸多领域[1]。

伴随着控制理论的不断发展,对倒立摆的控制也出现了采用经典控制理论、现代控制理论和人工智能控制理论等多种控制理论的方案和控制方法。本文首先建立了直线一级倒立摆的数学模型,并设计了PID控制器、极点配置法控制器、线性二次最优控制器,应用系统频率响应法进行分析与校正,最后用MATLAB软件进行仿真。

1 直线一级倒立摆建模及性能分析

1.1 数学模型建立[2]

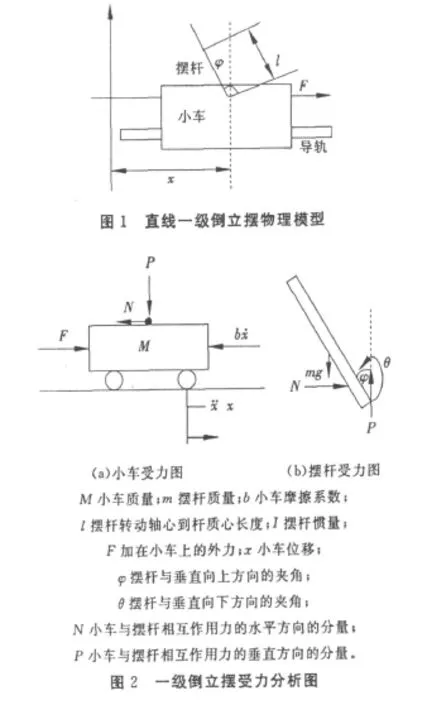
在忽略了空气阻力和各种摩擦之后,可将直线一级倒立摆系统抽象成小车和匀质杆组成的系统,如图1所示,而小车及摆杆受力分析见图2所示,其机械部分遵守牛顿运动定律,其电子部分遵守电磁学的基本定律,因此可以通过机理建模得到系统较为精确的数学模型。

用u表示被控对象的输入力F,应用牛顿运动定律,得到线性化微分方程表达式:

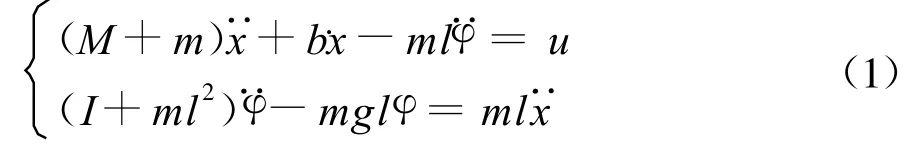
进而分别得到直线一级倒立摆在经典控制理论和现代控制理论中的数学模型。

(1)以输入力u为输入量,以摆杆摆角φ为输出量的传递函数:

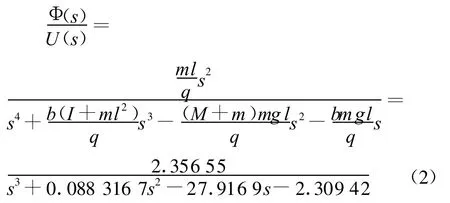
其中,q=(M+m)(I+ml2)-(ml)2

(2)以小车加速度v=¨x为输入,以摆杆摆角φ为输出量的传递函数:

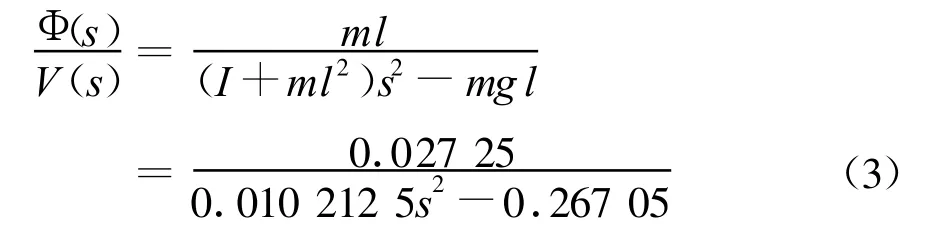
(3)状态空间表达式:

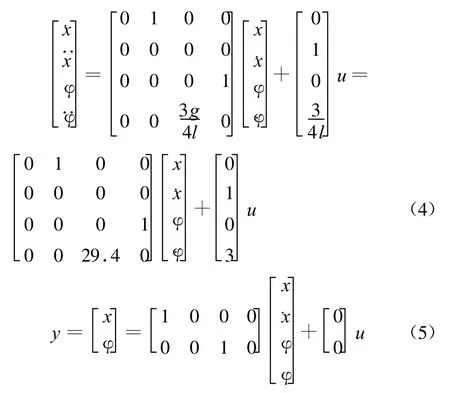
1.2 性能分析

应用模型1分析系统稳定性,用MAT LAB软件绘制系统阶跃响应曲线如图3所示,可知系统不稳定。应用模型3分析系统能控性和能观性,可知

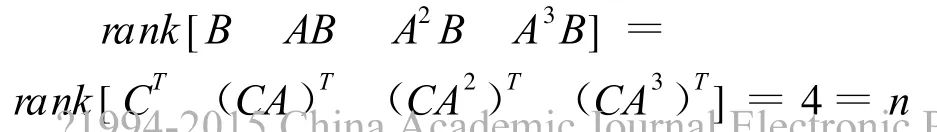
系统具有能控性和能观性。因此可以对系统进行控制器设计,使系统稳定。

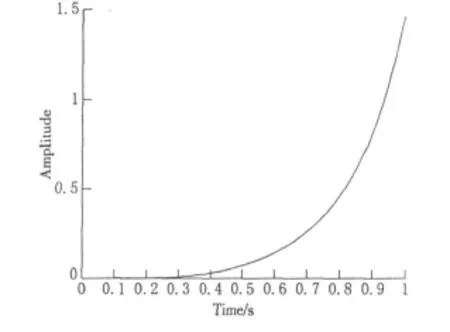
图3 一级倒立摆单位阶跃响应曲线

2 用经典控制法分析直线一级倒立摆

2.1 PID控制[3-4]

PID控制器结构简单,容易调节,且不需要对系统建立精确的模型,在实际控制中应用较广。对于本例,经过验证和总结前人的经验,可知一般的PID控制器只能对倒立摆摆杆的摆角进行控制,而不能对小车的位置进行控制,所以想到设计双闭环PID控制器。PID控制器主要在于参数的调整,可以根据经验确定,这里我们采用稳定边界法整定参数。对于公式(6)所示的PID控制器传递函数,

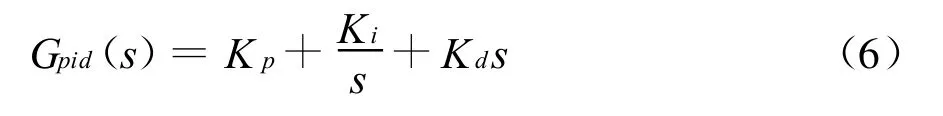
参数整定步骤如下:

(1)将控制器的积分系数Ki和微分系数Kd均设置为0,比例系数Kp设置为较小的值,使系统投入稳定运行。

(2)逐渐增大比例系数Kp,直到系统出现等幅震荡,并记录此时的临界震荡增益K和临界震荡周期T。

(3)根据K和 T的值,采用经验公式Kp=0.6K,Kd=0.125T,Ki=0.5T,计算出调节器的各个参数,即Kp、Ki和Kd的值。

通过反复实验,小车位置PID参数整定为:Kp=-85,Ki=-90,Kd=-67;摆杆PID参数整定为:Kp=230,Ki=0,Kd=60。在MAT LAB/SIMULINK环境下依据模型3建立一级倒立摆双闭环仿真模块如图4所示。仿真结果如图5～6所示,小车的位置,摆杆角度均能得到有效控制。

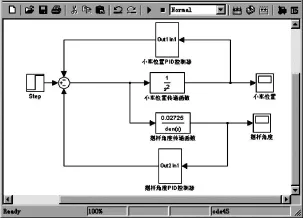
图4 PID控制仿真模块

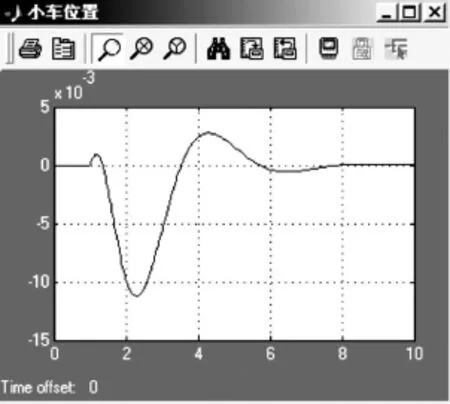
图5 PID控制小车位置仿真曲线

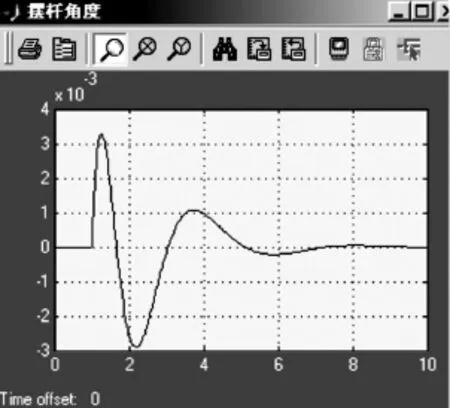
图6 PID控制摆杆摆角仿真曲线

2.2 频率响应分析与校正[5]

由数学模型2可以绘制其伯德图如图7所示,可知其相位裕量为0,采用超前校正装置进行校正,使得系统的稳态位置误差常数为10,相位裕量为50,增益裕量等于或大于10分贝。设超前校正装置

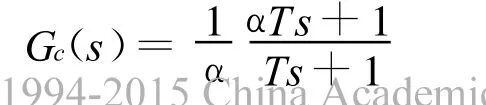
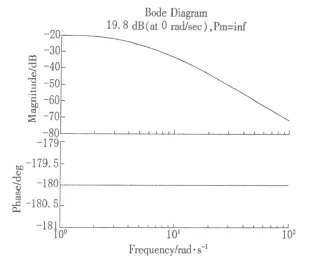
图7 串联校正前一级倒立摆的伯德图

根据误差要求得校正前系统传递函数为

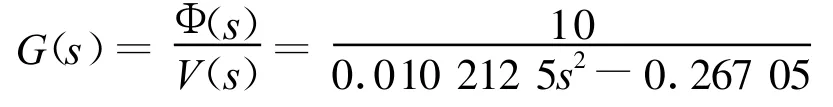
令 φm=50°+5°=55°,得到10.1,

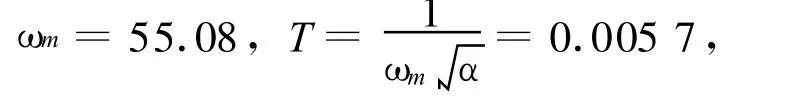
校正后系统传递函数为

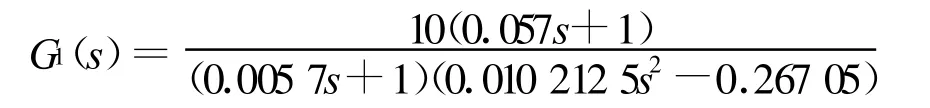
绘制其伯德图如图8所示,可知校正后系统的相角裕度和幅值裕度满足要求,可达到稳定状态。

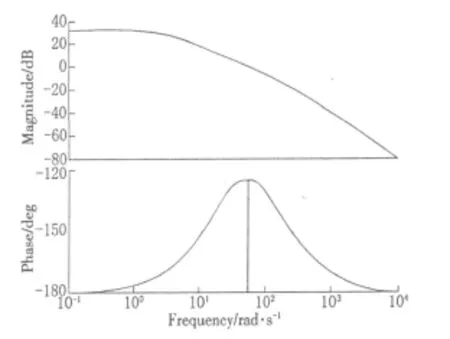
图8 串联超前校正后一级倒立摆的伯德图

3 用现代控制法分析直线一级倒立摆[6]

3.1 极点配置法

在1.2我们已经得到结论:一级倒立摆系统是状态可控的,所以可以通过状态反馈的方法将极点配置在期望的位置。这里反馈矩阵k可以采用系数匹配法、Ackermann配置算法和Gura-Bass算法。根据要求,并留有一定的裕量,我们选取期望的闭环极点为:

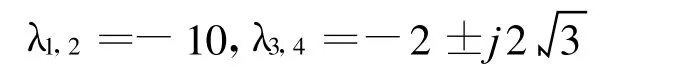
则根据期望的特征方程:

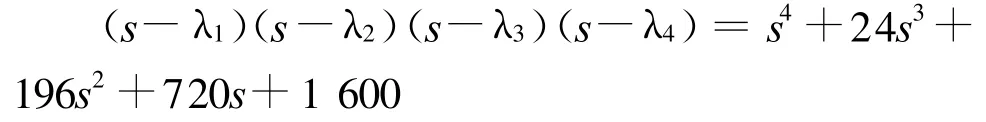
应用MAT LAB软件可以得到状态反馈增益矩阵为:

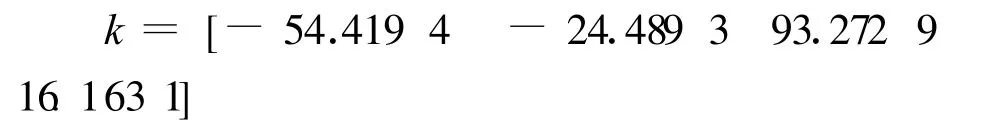
并得到一级倒立摆的仿真图如图9～10所示。

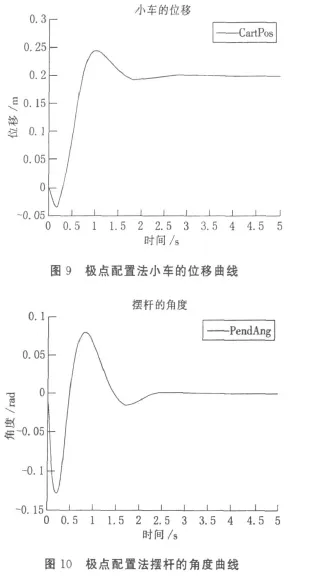
由以上的仿真图可知,极点配置法可以对倒立摆系统能够进行有效的控制,并且具有良好的稳态性能。

3.2 最优控制法

通过线性二次型最优设计方法在实际的倒立摆控制系统设计中得到了广泛的应用,具有较好的鲁棒性与动态特性以及能够获得线性反馈结构等优点。最优控制理论主要是依据Pontriagin极大值原理,通过对性能指标的优化来寻求使目标极小的控制器。

为了总结出Q1,1和Q3,3与系统响应时间的关系,我们通过改变 Q1,1和Q3,3后不断进行MAT LAB仿真实验,得到如下Q1,1和Q3,3与响应时间的关系表格。

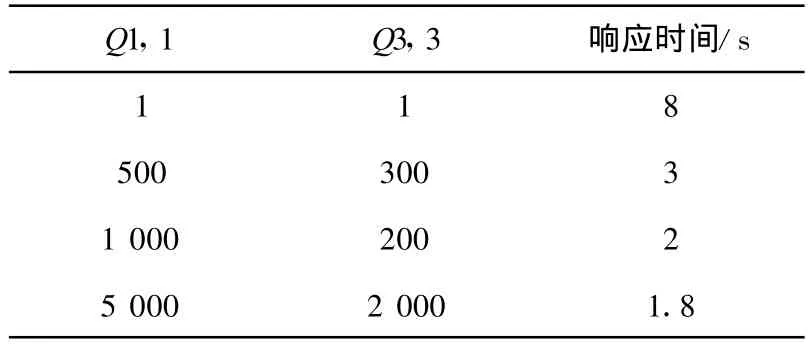
表1 Q1,1和Q3,3与响应时间的关系

本实例中我们可以选取Q1,1=1 000,Q3,3=200,此时摆杆角度的超调量足够小,同时上升时间也比较短。利用MAT LAB仿真可以得到仿真图如图11～12所示。

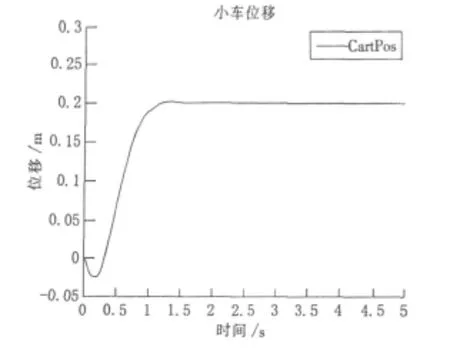
图11 最优控制小车的位移曲线

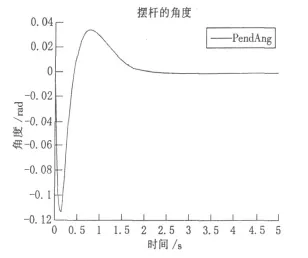
图12 最优控制摆杆的角度曲线

由仿真图可以看出,LQR控制器对小车的速度和摆杆的角度均有良好的控制效果,所以该算法对倒立摆的控制是有效的。

4 结语

本文以直线一级倒立摆为研究对象,在建立了其数学模型的基础上,分别从经典控制理论和现代控制理论出发分析系统的相关性能。从MATLAB仿真结果可知,PID控制可以更好地抑制超调,但调节时间较长。采用极点配置法,系统快速性较好,但超调量稍大。线性二次最优控制法则保证了稳定性和快速性,具有最优越的性能。

[1]张东军,丛爽.倒立摆控制系统研究综述[J].控制工程,2003,7(10):9-12.

[2]李晓燕.平面一级倒立摆系统的智能控制策略研究[D].山西:太原理工大学,2005:25-40.

[3]丛爽,张冬军,魏衡华.单级倒立摆三种控制方法的对比研究[J].系统工程与电子技术,2001,23(11):47-49.

[4]杨世勇,徐莉苹,王培进.单级倒立摆的PID控制研究[J].控制工程,2007,14(S0):23-24.

[5]胡寿松.自动控制原理[M].5版.北京:科学出版社,2007:243-296.

[6]郑大钟.线性系统理论[M].2版.北京:清华大学出版社,2002:254-370.