随机激励下非线性振动系统特性的定性分析
2010-06-08孔宪仁杨正贤徐大富
孔宪仁,廖 俊,杨正贤,徐大富
(哈尔滨工业大学 卫星技术研究所,哈尔滨 150086)
0 引言
结构在随机振动试验时,有时会超出线弹性范围,此时线性模型已经不能满足需要,为正确地研究结构特性,需要建立非线性模型。非线性动力学系统的辨识通常有3个步骤:一是识别非线性的存在;二是判别非线性的性质;三是建立系统的非线性模型进行参数识别。目前判别非线性的存在已经比较成熟,主要有幅值域、频域、时域方法[1]。
定性研究包括系统非线性的定位、非线性类型、非线性方程几种,本文集中研究非线性类型这部分。Feldmen 研究了时域中应用Hilbert变换判别随机激励下系统非线性类型的方法[2];Stasze 应用小波变换、Franco 应用Gabor 变换研究了系统非线性定性方法[3];K.Worden[4]等研究了正弦激励下非线性系统频响函数图及奈奎斯特图随外激励量级变化而发生的变形,根据系统分别存在非线性阻尼和非线性刚度时变形的规律不同而由此判断系统中非线性的类别,并给出了非线性定性分析的准则。本文参考文献[4]的准则,旨在给出随机激励下,通过系统频响函数图及奈奎斯特图随外激励量级的变化进行定性分析的方法,并将系统扩展到多自由度上。
本文对几种带有非线性因素的系统模型进行了近似求解,并分别画出了它们的等效频响函数图及奈奎斯特图,得到随机激励下系统频响函数随外激励量级的变化规律,从而给出了适用于随机激励的,通过等效频响函数随激励量级变化的趋势来判别系统非线性特性的方法。
1 解李雅普诺夫方程求随机响应方差
对于线性时不变系统可以写成方程[2]
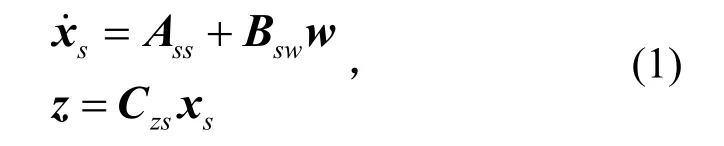
式中:sx为状态向量;w为输入向量;z为输出向量;A、B、C为响应维数的常量矩阵;下标s、w、z表示矩阵维数。
假设输入为白噪声,则输入的功率谱矩阵为对称正定的常量矩阵Wuu。状态变量的稳态协方差矩阵表示为

其中Xss为协方差矩阵。
容易证明式(2)满足李雅普诺夫方程
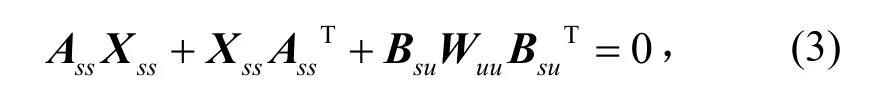
其中W为激励w的功率谱矩阵乘以2π得到的矩阵。
对ssA进行特征值分解,则得

式中:ssE为特征向量构成的矩阵;ssΛ为特征值构成的对角线矩阵。
经过矩阵推导求得李雅普诺夫方程的解的矩阵形式为

式中:1矩阵为合适维数的矩阵元素全为1的矩阵;符号“./”表示矩阵之间对应元素的相乘运算。
得到输出z的均方根(RMS)值为

这样仅通过式(5)和式(6)矩阵运算即可以求得所有响应点均方根值(或方差)。
对于一般线性结构的动力方程
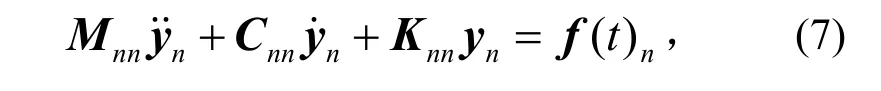
可令

式中:Mnn、Cnn、Knn分别为系统的质量、阻尼和刚度矩阵;I为n乘以n维的单位矩阵;Onn为元素为零的n乘以n维矩阵。
将式(8)代入式(5)、(6)即可很方便地得到随机激励作用下响应的方差。采用适当Czs矩阵可以获得响应的位移、应力的方差值以及von mises屈服应力等。令Czs=[InnOnn],可以得到响应位移的方差值。
上述过程也可以使用模态叠加方法进行缩减,再采用适当的Czs将方差值从模态坐标返回到原坐标下。
将式(7)通过模态变换到模态坐标下[3],则得

其中Mmm、Zmm、Ωmm、Φnm分别为模态质量、模态阻尼比、固有频率和模态的矩阵。经过推导可以得到模态坐标下的李雅普诺夫方程及其解法。
可令
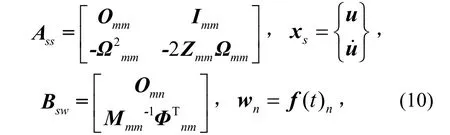
当Czs=[ΦnmOnm],通过式(4)、(5)、(6)即可解出各自由度位移响应的方差值。
2 等效线性化方法[1,5]
从非线性随机振动工程分析的角度来看,如果非线性程度不是太强,不考虑分叉、跳跃等本质非线性现象,则等效线性化法已经取得了较大的进展,是相对有效且简单可行的方法,是工程实际中最具有应用潜质的预测非线性系统随机响应的近似方法[6]。其基本思想为用有精确解的线性系统代替给定的非线性系统,并使两方程之差在某种统计意义上最小。文献[7]比较了以能量差为基础以及以方程差为基础的等效线性化方法计算的随机振动响应,认为以能量差为等效准则的方法效果要好。
考虑具有随机激励的单自由度非线性系统,其动力学方程为
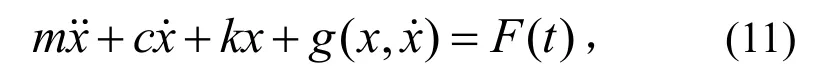
其中: (,)gxx˙为非线性项,m、c、k分别为系统质量、阻尼、刚度。建立等效的线性化方程
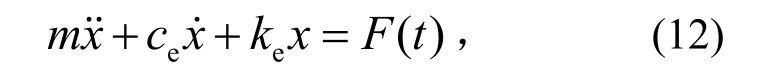
其中ce、ke为等效的阻尼系数和刚度系数。以能量差最小为准则可求得ce、ke分别为
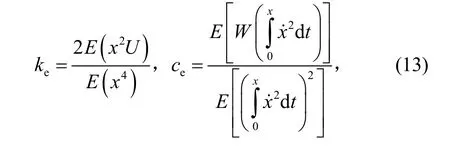
以方程差为基础的等效阻尼系数和刚度系数可通过下式获得[7]:

先设定ce、ke的一个初始值,求解式(11)得到x的某统计值,代入式(13)或(14)求得新的等效系数。经过反复迭代后得到所求的值。一般将式(11)的等效系数的结果化成E(x⋅xT)的形式或其中的元素来表示,这正是式(2)得到的解,用它来参与迭代,效率和精度将得到很大的提高。只需通过式(8)或者式(10)转换成状态空间表示的运动方程,其协方差矩阵即可求得,并参与到等效线性化的迭代计算中,从而获得稳定的等效线性化的系数。本文采用能量差为准则的等效线性化方法对系统进行处理。
3 几种情况下的非线性特性研究
根据线性等效原理,等效频响函数为
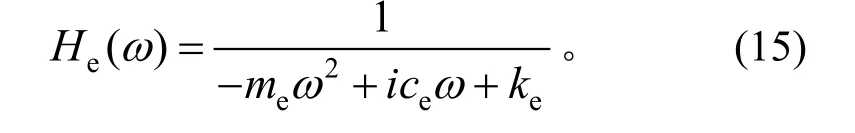
将几种情况下的近似解分别代入式(15)即可得到存在于不同非线性特性系统的等效频响函数。
3.1 单自由度情况

令m=1、c=5、k=100,功率谱S0分别为1、4、8、12,ε=1时为硬弹簧,ε=-1时为软弹簧;则不同量级随机激励下的硬弹簧和软弹簧的等效频响函数图与奈奎斯特图如图1~图4所示。
由图1~图4可以看出,当存在非线性刚度时,系统频响函数随着激励量级增大而发生改变。当K3>0时,图1中系统固有频率随激励量级增加而增加,发生向上移频现象;图2中奈奎斯特图向内收缩,系统呈现典型的单自由度硬弹簧性质[8]。由图3、图4可知,当K3<0时,图3中系统固有频率随外加激励量级增加而降低,发生向下移频现象;图4中奈奎斯特图向外膨胀,呈现软弹簧性质。在随机激励试验中,可应用不同量级的频响函数曲线与外激励的变化规律定性地分析系统中存在的非线性类型,从而指导系统建模。

图1 不同量级随机激励下硬弹簧等效线性化频响函数图(k3>0)Fig.1 Linearized FRF of a cubic stiffness model for different levels of random excitation(k3>0)
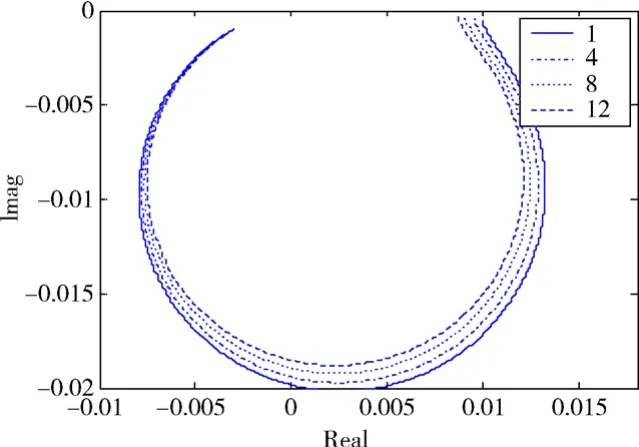
图2 不同量级随机激励下硬弹簧等效奈奎斯特图(k3>0)Fig.2 Nyquist plot of a cubic stiffness model for different levels of random excitation(k3>0)
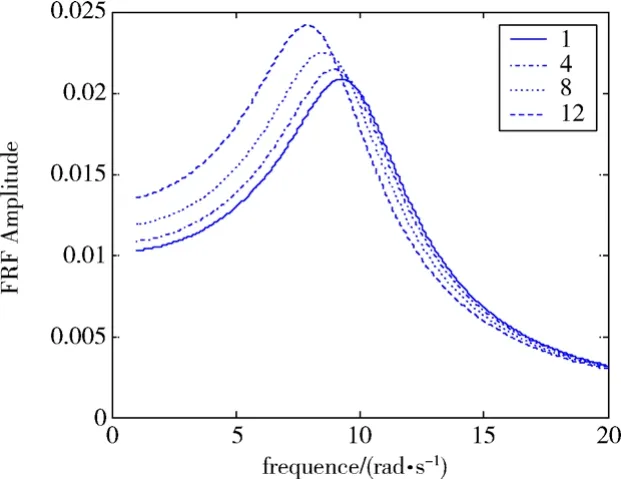
图3 不同量级随机激励下软弹簧等效线性化频响函数图(k3<0)Fig.3 Linearized FRF of a cubic stiffness model for different levels of random excitation(k3<0)
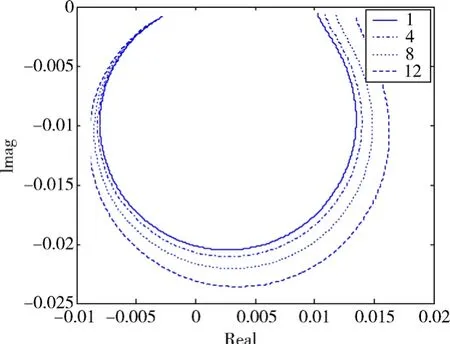
图4 不同量级随机激励下软弹簧等效奈奎斯特图(k3<0)Fig.4 Nyquist plot of a cubic stiffness model for different levels of random excitation(k3<0)
3.2 二自由度情况
图5为一个二自由度的系统,两个质量块之间存在非线性弹簧。
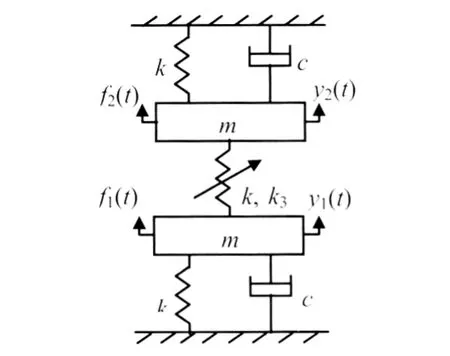
图5 二自由度系统模型Fig.5 A 2 DOF model
3.2.1 非线性硬弹簧在两质量块之间非线性硬弹簧的动力学方程为
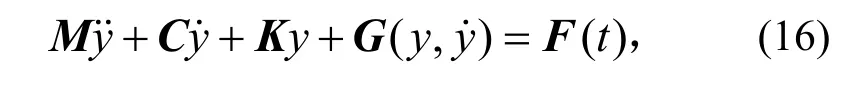
式中:

其中m=1,k=3 000,k3=2×108,c=20。激励功率谱S1=S2,分别为1、1.5、2、2.5。该系统经过变量替换可变换成一个线性单自由度系统和一个带非线性硬刚度单自由度系统的叠加[4],这在系统频响函数中得到体现,见图6、图7。

图6 不同量级二自由度H11等效线性化频响函数图Fig.6 Linearized FRF of H11 for a 2 DOF system under different levels of random excitation

图7 不同量级二自由度频响函数H11等效奈奎斯特图(k3>0)Fig.7 Nyquist plot of H11for the 2 DOF system under different levels of random excitation (k3>0)
图6显示,随着激励量级的增加,频响函数在第一等效共振频率处未发生频率漂移,在第二等效共振频率处频率向上漂移;图7显示,随着随机激励量级增大,奈奎斯特图的小圆出现明显向内收缩。这说明在第二阶模态上存在硬弹簧的非线性特征。这也证明了该方法对于非线性特性分析的正确性。对于其他3个频响函数也有类似特征,限于篇幅不予详述。
3.2.2 非线性硬弹簧与地面相连
将图 5中非线性的弹簧与连接地面和质量块的弹簧进行互换,其运动方程形式见式(16)。此时的系统两个自由度的运动方程都包含了非线性。限于篇幅只取了4个频响函数中的H11和H12进行分析计算,其他情况也可采用类似方法进行分析。式(16)中各常量的定义分别为
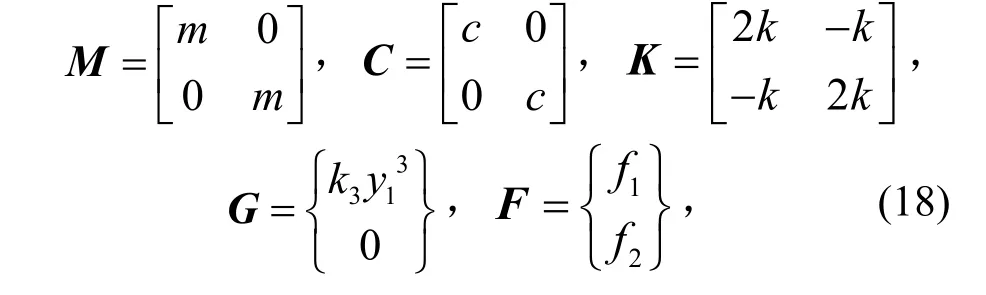
其中m=1,k=3 000,k3=2×108,c=20。激励功率谱S1=S2,分别为 1、2、4、8。
分析计算结果见图8~图11,其中:图8、图9分别为频响函数H11的幅值图和奈奎斯特图;图10、图11分别为频响函数H12的幅值图和奈奎斯特图。

图8 不同量级二自由度H11等效线性化频响函数图Fig.8 Linearized FRF of H11 for the 2 DOF system under different levels of random excitation
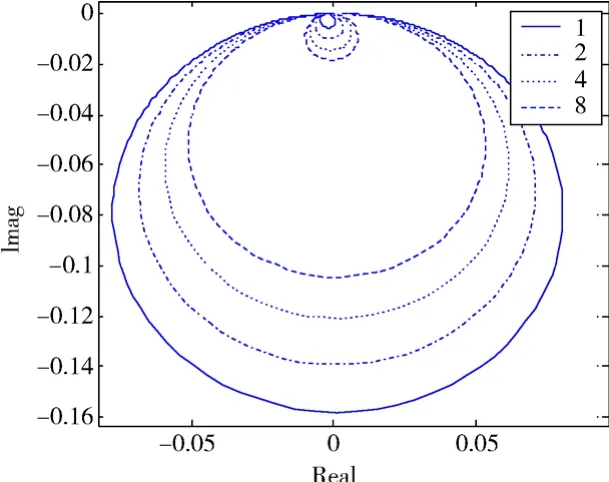
图 9 不同量级二自由度频响函数H11等效奈奎斯特图Fig.9 Nyquist plot of H11 for 2 DOFs system under different levels of random excitation

图10 不同量级二自由度H12等效线性化频响函数图Fig.10 Linearized FRF of H12 for the 2 DOF system under different levels of random excitation

图11 不同量级二自由度频响函数H12等效奈奎斯特图Fig.11 Nyquist plot of H12 for the 2 DOF system under different levels of random excitation
图8和图10显示,在两个自由度上,随着激励量级的增大,都有固有频率向上移动,这与硬弹簧的特性相同;随着激励量级的增大,图9中的小圆是向外扩张的,图11中的两个圆都有向外扩张的现象,这是单自由度情况下软弹簧的特点。可见,多自由度因为存在模态之间的能量传递,使得其非线性特性有了自身的特点,不能简单用单自由度的方法来分析。
4 结论
本文采用随机激励源,应用求解李雅普诺夫方程与等效线性化法对非线性特性进行了定性的研究。分别对单自由度与二自由度振动系统在随机激励下的非线性特性进行了分析,并给出了等效频响函数及奈奎斯特图随激励量级变化的规律,根据变化规律的不同给出随机激励下系统非线性定性研究的方法,对非线性动力学系统的定性研究及建模有一定的工程应用价值。
(References)
[1]朱位秋.随机振动[M].北京: 科学出版社, 1998
[2]Feldoman M.Nonlinear system vibration analysis using Hilbert transform-II forced vibration analysis method‘Forcevib’[J].Mechanical Systems and Signal Processing,1994, 8(3): 309-318
[3]Gaëtan Kerschen.Past, present and future of nonlinear system identification in structural dynamics[J].Mechanical Systems and Signal Processing, 2006, 20: 505-592
[4]Worden K, Tomlinson G R.Nonlinearity in structural dynamics: detection, identification and modelling[M].Insitute of Physics Publishing, 2001
[5]Elishakoff I, Zhang X.An appraisal of different stochastic linearization techniques[J].Journal of Sound and Vibration, 1992, 153(2): 370-375
[6]朱位秋.非线性随机振动理论的近期进展[J].力学进展, 1994, 24(2): 163-173
[7]罗务揆, 邢誉峰, 杨蓉.辛算法在随机振动响应求解中的应用[J].航空动力学报, 2008, 23(1): 37-43
[8]何蕊, 罗文波, 王本利, 等.基于Lyapunov指数的铝蜂窝板频率漂移机理分析[J].宇航学报, 2009, 30(2):463-467
