临近空间大气中子诱发电子器件单粒子翻转数值仿真研究
2010-06-08张振力蔡明辉韩建伟张振龙
张振力, 蔡明辉, 韩建伟, 张振龙
(1.中国科学院 空间科学与应用研究中心,北京 100190;2.中国科学院 研究生院,北京 100049)
0 引言
临近空间指离地面高度为20~100 km的区域。近年来,因其在科学研究和经济上的重要性,已引起了国际上的广泛关注[1]。大气中子是临近空间的主要辐射粒子,并且是这一区域诱发电子器件发生单粒子翻转最主要的原因,严重威胁着临近空间飞行器安全、可靠地工作[2-3]。20世纪80年代末,IBM和 Boeing公司联合开展了高空大气中子诱发器件单粒子效应的飞行试验研究,试验结果充分证明了大气中子能够诱发器件发生显著的单粒子效应[4]。随着器件加工工艺的不断发展,器件单元尺寸不断缩小,工作电压不断降低,使得器件抵御单粒子效应的能力不断降低,因此临近空间大气中子诱发器件发生单粒子效应的潜在危害也越来越大[5]。
本文研究了临近空间大气中子在不同时间、经度、纬度、高度下的能谱,计算结果和国外模型计算结果符合很好。计算了静态存储器(SRAM)中的 IMS1601芯片在不同能量各向同性的中子入射下的翻转截面,计算结果和地面试验结果符合较好。在国内首次计算出临近空间任意两地间飞行器上的 IMS1601芯片的翻转率,计算结果和国外飞行试验结果基本符合。
1 计算方法
1.1 大气中子能谱计算

图1 大气中子模型示意图Fig.1 The model of atmospheric neutron
大气中子是银河宇宙线、太阳质子与地球大气中的氧、氮等元素发生核反应生成的次级粒子。大气中子仿真计算模型的基本思路如图1所示[5]。首先计算不同时间下银河宇宙线和太阳宇宙线质子能谱;然后考虑地磁场对质子的屏蔽作用,计算不同位置的地磁截止刚度,得到不同位置的质子能谱;接着计算不同高度的大气成分;最后开始计算机仿真计算,得到大气中子能谱。大气中子能谱随经、纬度的变化主要归因于地磁截止刚度随经、纬度的变化,随高度的变化主要归因于大气成分随高度的变化。为了简化计算,首先用蒙特卡罗软件 FLUKA[6-7]计算出不同能量的单能质子在不同高度产生的中子能谱,然后计算出地磁截止刚度与经、纬度之间的关系,最后结合不同时间下银河宇宙线及太阳宇宙线的质子能谱,计算出不同的地磁截止刚度对应的中子能谱。这样一来输入时间、经度、纬度、高度就可以计算出该点的中子能谱。输入时间分3种情况考虑——太阳活动低年、太阳活动高年和太阳质子事件最强当天,太阳质子事件最强当天以1989年10月20日为例。本文的模型可以计算中子能谱的高度范围是0~100 km,经度、纬度覆盖全球。
1.2 单粒子翻转截面计算
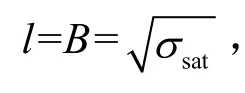
敏感体积内产生的次级重离子可以引起单粒子翻转,敏感体积附近产生的次级重离子也可以进入器件的敏感体积引起单粒子翻转。中子能量达到150 MeV时,中子诱发器件的翻转截面达到饱和[10]。为了确定敏感体积附近对单粒子翻转有贡献的区域大小,本文对500 MeV的中子与Si反应产生的次级重离子的射程进行了模拟计算,计算结果显示次级重离子在 Si中的射程绝大多数小于 4 μm。SRAM由多个存储单元构成,各个存储单元的单粒子翻转是相互独立的。为了节约计算时间,建立模型的时候只考虑一个存储单元[9]。敏感体积及其附近对单粒子翻转有贡献的区域称为相互作用区,相互作用区可简化为一个长宽高都比敏感体积的长宽高大8 μm(向两侧各拓展4 μm)的长方体。敏感体积设置为体探测器,用来记录每一次中子入射产生的所有次级粒子在敏感体积内的总沉积能量。中子单粒子翻转模型如图2所示。

图2 中子单粒子翻转模型立体示意图Fig.2 The 3-D sketch of the model of single event upset induced by neutron
翻转截面hid()Eσ与沉积能量dE之间的关系通常用Weibull函数描述,表达式为

其中:thE为引起翻转的临界能量;W为宽度因子;S为形状因子。
试验结果显示,热中子(中子与周围介质处于热平衡状态,其动能相当于分子热运动的能量。对于20 ℃,能量为0.025 3 eV)与10B反应也可以诱发单粒子翻转,但若改进半导体制作工艺,取代半导体中的掺杂元素10B,就可以大大减小热中子诱发器件的翻转截面[10]。除热中子外,10 MeV以下的中子诱发器件的翻转截面很小,因此本文忽略了能量低于10 MeV的中子诱发器件的翻转截面。翻转截面的计算可参考文献 [11],本文用GEANT 4软件[12-13]分别计算了10 MeV、15 MeV、30 MeV、50 MeV、100 MeV、150 MeV的6种能量中子各向同性入射时在敏感体积内沉积能量的积分能谱N(En,Ed)(沉积能量≥Ed的几率),其中En为中子能量。通过计算可以得到相应的微分能谱N'(E,E)。考虑到芯片对一定沉积能量E具有
n dd翻转截面σhi(Ed),则能量为En的中子引起的翻转截面为

将式(1)带入式(2),则得到

具体计算某一芯片的翻转截面时,可分别先计算10 MeV、15 MeV、30 MeV、50 MeV、100 MeV、150 MeV的6种中子诱发器件的翻转截面,其他能量的中子诱发器件的翻转截面采用指数插值的方法获得。
1.3 飞行过程中单粒子翻转率的计算
已知飞行航线的前提下,根据中子能谱与经度、纬度之间的对应关系以及翻转截面与中子能量之间的对应关系,就可以计算出某一芯片在飞行过程中的翻转率[11]

其中n()Eφ表示航天器在飞行过程中遭遇到的中子全向微分通量。
2 计算结果及验证
2.1 中子微分能谱和国外模型的对比
本文以太阳活动低年、20 km、北纬89°、东经45°为例计算中子微分能谱,为了验证结果的正确性,与国外模型 EXPACS进行了对比。EXPACS模型由日本原子能机构开发,得到了广泛认可[14]。本文计算结果与EXPACS结果如图3所示,对比发现结果符合很好。

图3 中子微分能谱对比图Fig.3 Comparison between differential spectra of neutrons
2.2 翻转截面模拟计算和地面试验结果的对比
本文以SRAM器件中的IMS1601芯片为例,计算其翻转截面随中子能量的变化关系,具体的器件参数参考文献[15]、[16]中的数据,如satσ=916 μm2/bit,h=5.5 μm,thE=3.84 MeV,W=13.5 MeV,S=1.2。为了和地面试验结果进行对比,本文除了计算各向同性入射的中子诱发器件的翻转截面外,也模拟了垂直入射的中子诱发器件的翻转截面。文献[2]报道了 IMS1601芯片的部分中子辐照试验结果。当中子能量大于50 MeV时,中子诱发器件的单粒子翻转截面与质子诱发器件的单粒子翻转截面相当[10]。针对 IMS1601芯片的高能中子的辐照试验数据缺乏,文献[15]报道了该器件高能质子的辐照试验结果。因此将中子的各向同性入射、垂直入射模拟计算结果,中子地面试验结果与高能质子试验结果绘制在同一图中,如图4所示,对比发现模拟计算结果和地面试验结果符合较好。

图4 翻转截面与中子能量之间的关系Fig.4 Relation between upset cross section and neutron energy
2.3 翻转率模拟计算和飞行试验结果的对比
IBM和Boeing公司联合开展了器件翻转率的飞行试验,对IMS1601芯片的翻转率进行了测试。文献[2]、[15]报道了飞行试验的位置和时间,通过数据调研得到1号航线和2号航线的飞行时间为太阳活动低年,3号航线为太阳活动高年[17-18]。本文对 IMS1601芯片的翻转率进行了模拟计算,计算结果和飞行试验结果如表1所示。
对比发现结果存在一定偏差。引起偏差的主要原因是翻转率的计算结果依赖于中子能谱和中子诱发器件的翻转截面的计算结果,而这两者都与真实情况存在着差异,最后导致翻转率模拟计算结果与实际飞行试验结果的偏差。但这种偏差都在同一数量级内,计算结果仍具有一定可信度。

表1 翻转率模拟计算与飞行试验结果对比Table 1 Comparison of SEU rate between simulation and flight test results
3 结束语
本文给出了临近空间大气中子诱发器件单粒子翻转率估算方法,计算出临近空间任意位置的中子能谱,计算了已知器件参数的IMS1601芯片在各向同性中子入射下的翻转截面,以及任意两个临近空间位置上飞行器的 SRAM 器件的翻转率。
本文模拟计算得到的翻转率与国外飞行试验结果基本符合。尽管存在差异,但这种简便快捷的计算方法给出的结果仍然是可信的,可为临近空间航天器的设计、制造及实际飞行提供指导作用。
(References)
[1]曹秀云.近空间飞行器成为各国近期研究的热点(上)[J].中国航天, 2006(6): 32-36
[2]Taber A, Normand E.Single event upset in avionics[J].IEEE Trans Nucl Sci, 1993, 40(2): 120-126
[3]Olsen J, Becher P E, Fynbo P B, et al.Neutron-induced single event upsets in static RAMs observed at 10 km flight altitude[J].IEEE Trans Nucl Sci, 1993, 40(2):74-77
[4]Normand E.Single-event effects in avionics[J].IEEE Trans Nucl Sci, 1996, 43(2): 461-474
[5]蔡明辉, 韩建伟, 李小银, 等.临近空间大气中子环境的仿真研究[J].物理学报, 2009, 58(9): 6659-6664
[6]Battistoni G, Muraro S, Sala P R, et al.The FLUKA code:description and benchmarking[C]//Proceedings of the Hadronic Shower Simulation Workshop 2006, AIP Conference Proceeding 896, 2007: 31-49
[7]Fasso A, Ferrari A, Ranft J, et al.FLUKA: a multiparticle transport code, CERN-2005-10[R], INFN/TC_05/11,SLAC-R-773
[8]李华.静态随机存储器单粒子翻转的Monte Carlo模拟[J].物理学报, 2006, 55(7): 3540-3545
[9]杨海亮, 李国政, 李原春, 等.质子和中子引起的单粒子效应及其等效关系理论模拟[J].原子能科学技术,2001, 35(6): 490-495
[10]Baggio J, Ferlet-Cavrois V, Duarte H, et al.Analysis of proton/neutron SEU sensitivity of commercial SRAMs—application to the terrestrial environment test method[J].IEEE Trans Nucl Sci, 2004, 51(6):3420-3426
[11]韩建伟, 叶宗海.质子引发的单粒子翻转率估算的研究[J].空间科学学报, 1999, 19(3): 266-271
[12]Allison J, Amako K, Apostolakis K.Geant4 developments and applications[J].IEEE Trans Nucl Sci, 2006, 53(1):270-278
[13]Santin G, Nartallo R, Nieminen P, et al.Geant4 in the space environment: tools and applications[C]//Proc Nuclear Science Symposium Conference Record, IEEE,2003: 1522-1526
[14]Sato T, Niita K.Analytical functions to predict cosmic-ray neutron spectra in the atmosphere[J].Radiat Res, 2006,166(3): 544-555
[15]Taber A H, Normand E.Investigation and characterization of SEU effects and hardening strategies in avionics,DNA-MIPR-92-501[R], 1995
[16]Norugmand E.Extensions of the burst generation rate method for wider application to proton/neutron-induced single event effects[J].IEEE Trans Nucl Sci, 1998, 45(6): 2904-2914
[17]都亨, 叶宗海.低轨道航天器空间环境手册[M].北京: 国防工业出版社, 1996: 348
[18]Naval Research Laboratory.The cosmic ray effects on micro-electronics(1996 revision)[EB/OL].[2009-09-10].http://creme96.nrl.navy.mil
