考虑初始几何缺陷的大型钢板筒仓构造措施的研究

2010-06-05敖晓钦陈向荣

水利与建筑工程学报 2010年1期

敖晓钦,陈向荣

(1.中铁上海设计院集团有限公司,上海 200070;2.西安建筑科技大学土木工程学院,陕西西安 710055)

1 筒仓概况及初始缺陷型式

筒仓实例如图1,环向加劲肋L140×12,竖向加劲肋-80×10@1200。施工时筒仓必须满足《钢结构工程施工质量验收规范》[1]的有关规定,本文以该规范作为考虑初始几何缺陷的取值依据,每段拼接板带的允许弯曲矢高为 δ0=L/1000,L为拼接板带高度。板带在两侧焊缝处产生凹陷,中部无凹陷,板带凹陷形状如图2所示,图中虚线表示筒仓中心线,R为筒仓半径。则板带中环向焊缝产生的凹陷形式按(1)式取值:

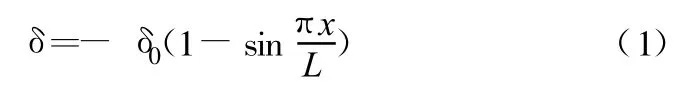
式中:δ0为焊缝收缩凹陷的峰值;L为拼接板带高度;x为板带任一点至板带边焊缝距离。

拼接板带每段高L=2000mm,所以,δ0=L/1000=2mm,为拼接板缺陷处的最大值。

采用ANSYS有限元程序对图1筒仓筒体按实际设计情况进行建模分析,仅对筒仓加劲肋的位置及尺寸的取值做改变,同时对筒仓的每段钢板按图2考虑初始缺陷。建模采用的钢材材料参数按《钢结构设计规范》[2]采用,材料为理想弹塑性,本构关系如图3所示[3,4]。

图1 落地式钢筒仓立面图(t为筒仓壁板厚,mm)

图2 环向轴对称缺陷形式

图3 理想弹塑性材料本构关系

2 加劲肋不同位置筒仓稳定性数值分析

筒仓加劲肋的设置范围有20 m～29.123 m(上部)、10 m～20 m(中部)及0～10 m(下部)三种情况。经过几何非线性分析,无论加劲肋设置在何处,筒仓的最大Mises应力都发生在筒仓底部,说明筒仓在受力时其底部更易屈服,因此应采取对其底部进行加强的构造措施。

三种情况下的筒仓结构在实际荷载[5]作用下材料均未屈服,总体上均是仓壁顶部的应力较小,随着深度的增加仓壁的应力也逐渐的增大,但在三种情况下筒仓结构的应力分布有较大区别,应力大小的分布范围不同。加劲肋设置在上部时的大应力分布范围相对较加劲肋设置在中部的大,而加劲肋设置在中部的大应力范围分布范围又相对较加劲肋设置在下部的更大。此处大应力分布范围是指仓壁应力σ＞110 N/mm2的分布范围。当筒仓上施加荷载为筒仓实际荷载时,加劲肋设在不同部位时筒仓产生的最大Mises应力分别为 f上=196 N/mm2、f中=196 N/mm2、f下=172 N/mm2,即f上=f中＞f下。这些都说明加劲肋设置在下部时对提高筒仓的承载力更有利。因为加劲肋有相当于增加钢板筒仓壁厚的作用[6],而同时最大应力发生在筒仓的底部,所以加劲肋设置在底部更有效,且能降低初始几何缺陷的影响[7]。

筒仓在实际荷载作用下,三种情况的最大Mises应力均小于材料屈服强度,表明所加荷载未达到极限荷载。现将所加荷载放大一倍作用到筒仓上,对比加劲肋在三种情况下筒仓极限承载力及位移的变化。

图4为三种不同加劲肋设置情况的荷载位移曲线图,纵坐标为施加荷载与加劲肋设置在底部时极限荷载的比值,无量纲,横坐标为产生的位移(mm)。

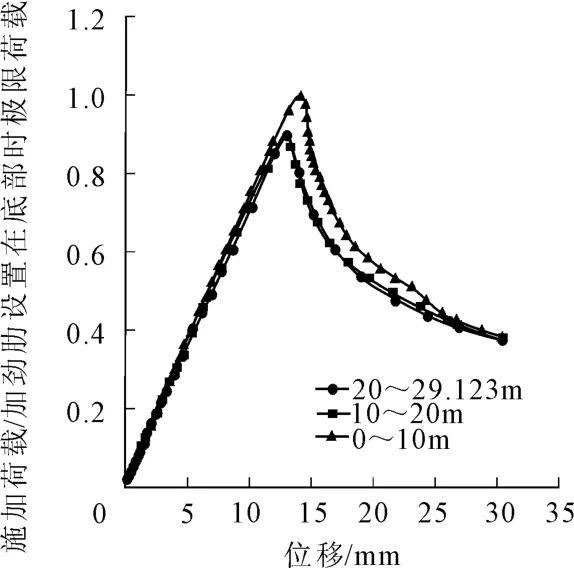
图4 荷载位移

从图4可知,当加劲肋设置在筒仓的底部时极限承载力最大,加劲肋设置在中部或者上部时筒仓的极限承载力约为加劲肋设置在底部时筒仓极限承载力的0.9倍,因此加劲肋设置在筒仓底部对提高筒仓的稳定性更有利,能有效提高其承载能力。

3 不同加劲肋构造筒仓稳定性数值分析

针对加劲肋设置在筒仓下部的情况,得到合理的加劲肋设置范围,并对环向加劲肋的厚度、宽度和竖向加劲肋的间距、宽度、厚度以及各自的宽厚比进行分析。

3.1 加劲肋设置高度变化

有限元模型建立时,环向和竖向加劲肋在筒仓底部设置,高度沿底部逐渐增加,从底部按每2000mm增加一个环向加劲肋,相应的竖向加劲肋沿高度方向增加2000mm,环向和竖向加劲肋相应尺寸均维持设计不变,其特征值屈曲承载力变化如图5。

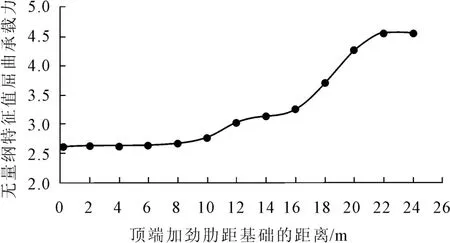
图5 加劲肋沿高度增加时筒仓无量纲特征值屈曲承载力

从图5可知,随着加劲肋设置范围不断增加,筒仓屈曲承载力不断提高,加劲肋设置在0～10 m至0～22 m段提高明显,设置小于0～10 m及高于0～22 m段变化较小。因此可采用增加加劲肋设置范围来提高筒仓极限承载力。考虑经济性及受力情况,取加劲肋设置在0～16 m分析环向和竖向加劲肋尺寸变化对极限承载力的影响。

3.2 环向加劲肋变化

当环向和竖向加劲肋设置在0～16 m时,变化环向和竖向加劲肋宽度及厚度,对比其承载力情况,得出合理的加劲肋尺寸。

3.2.1 环向加劲肋宽度变化

环向加劲肋宽度b1从60mm每隔20mm增加到180mm(其余尺寸维持与实例不变),对比其特征值屈曲承载力,如图6所示。纵坐标为筒仓特征值屈曲临界荷载与筒仓实际荷载比值。

由图6可知,特征值屈曲承载能力随着b1的增加而增大,但增大的幅度较小,几乎可以忽略不计。因此环向加劲肋宽度对钢板筒仓稳定性影响较小,但环向加劲肋不设时筒仓极限承载力下降较大,所以应选择较为合适角钢作为环向加劲肋。因环向角钢沿筒仓圆周方向是一个非常细长的构件,考虑到其自身的刚度及稳定性,应采用钢板对环向角钢加劲肋进行加强。同时为了方便施工并考虑经济性及施工习惯,建议取 b1=125mm的角钢。

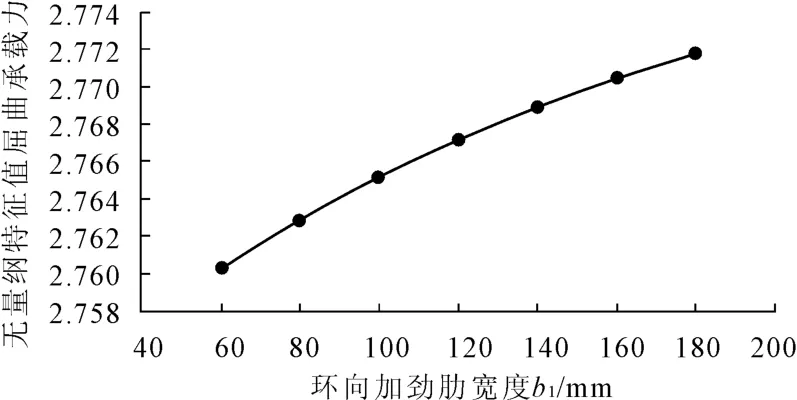
图6 不同环向加劲肋宽度无量纲特征值屈曲承载力

3.2.2 环向加劲肋厚度变化

环向加劲肋厚度t1从0每隔4mm增加到24mm(其余尺寸维持与实例不变),对比极限承载力。表1给出筒仓不同环向加劲肋厚度的屈曲荷载因子λ,λ为设加劲肋的极限荷载与无加劲肋极限荷载的比值。

表1 环向加劲肋厚度变化时筒仓屈曲荷载因子

t1=0为筒仓不设环向加劲肋的情况。由表1可知,屈曲荷载因子均为大于1的数,即设置环向加劲肋筒仓极限承载力均高于不设环向加劲肋筒仓极限承载力,提高10%以上,表明环向设置加劲肋可提高筒仓承载力,能降低初始缺陷对筒仓的敏感程度,对筒仓的整体稳定性有利。由表1可知,环向加劲肋厚度越大,筒仓极限承载力越高,但厚度变化对筒仓极限承载力提高不大,并不是环向加劲肋越厚越好,建议取 t1=10mm。

3.3 竖向加劲肋变化

3.3.1 竖向加劲肋宽度变化

竖向加劲肋宽度b2从80mm增加到150mm(其余尺寸维持与实例不变),对比其特征值屈曲承载力,如图7所示。纵坐标为筒仓特征值屈曲临界荷载与筒仓实际荷载比值。

图7 不同竖向加劲肋厚度无量纲特征值屈曲承载力

由图7可知,特征值屈曲承载力随竖向加劲肋宽度增大而增大,竖向加劲肋越宽对提高筒仓的稳定性有利。但宽度增大对提高其特征屈曲承载力不明显,特征值屈曲承载力相差不到3%。大可不必无谓增加竖向加劲肋宽度来提高筒仓承载力。为保证筒仓经济性,建议取b2=100mm。

3.3.2 竖向加劲肋厚度变化

竖向加劲肋厚度t2从4mm每隔2mm增加到20mm(其余尺寸维持与实例不变),对比其特征值屈曲承载力,如图8所示。纵坐标为筒仓特征值屈曲临界荷载与筒仓实际荷载比值。

图8 不同竖向加劲肋宽度无量纲特征值屈曲承载力

由图8可知,对竖向加劲肋设置间距为600mm～1600mm的各种情况,曲线趋势一致,均随着竖向加劲肋厚度的增加,筒仓承载力在增大的规律,且竖向加劲肋厚度在10mm之前的曲线斜率要大于在10mm之后的斜率,竖向加劲肋厚度t2＞10mm时曲线接近水平线。但厚度的增加对提高其特征屈曲承载力不明显,特征值屈曲承载力相差不到3%。因此不必无谓增加筒仓竖向加劲肋厚度来提高筒仓的承载力。为了保证筒仓经济性,建议取t2=10mm。

3.3.3 竖向加劲肋间距变化

由图8可知,筒仓的特征值屈曲承载力是随着间距的增大而减小,增大竖向加劲肋间距会降低筒仓的特征值屈曲承载力。但减小的幅度很小,不明显,特征值屈曲承载力最大值不会超过最小值的3%。由图8可见,筒仓竖向加劲肋间距取d=1600mm即可。