超磁机器鱼游动数值模拟及其控制

孙 发 明， 徐 新 生， 胡 俊 林， 杨 超

（大连理工大学 工业装备结构分析国家重点实验室，辽宁 大连 116024）

0 引 言

在医学领域和工业应用中，越来越迫切需要一种能在水或水介质中平稳灵活移动的新型管道微小型机器人[1].它能在水中被无线驱动，具有很高的机动性和灵活性，能够安全进入人体并且不会对各个器官造成负面影响.微小型机器人的最大优势就是能在非常小的空间内灵活工作.比如在医学方面，利用微小型机器人做一个精密手术能避免对患者手术开刀和缝补伤口，仅仅对受伤害的部位进行操作，而不影响周围的正常部分，将使患者的伤害减到最小.在工业上，也可利用微小型机器人去维护工业管道.目前有很多类型的微小型驱动器正在被研究，如Carrozza等[2]研究了用于结肠镜检查的基于蠕动爬行模式的形状记忆合金（SMA）驱动器.从仿生学角度看，该驱动器属于蠕动推进模式.梅涛等[3]模仿水母压水推进方式提出了仿水母型铁磁聚合体（FMP）驱动器.Saotome等[4]利用电磁铁设计了一种驱动器结构，实现了横向游动.Guo等[5]研制了能仿鱼尾摆动的离子传导聚合体膜（ICPF）驱动器，同时也提出一种能仿鱼尾摆动的新型电磁马达驱动器[6].Yamazaki等[7]设计了外磁场控制旋转前进的铁磁（Nd FeB）螺旋型驱动器.Jomie等利用电磁铁原理，设计出了可转弯的机器鱼驱动器[8].这些装置可控性和机动性有待改进.随着超磁致伸缩材料的出现和发展，更好地利用无线控制并设计特殊的机器鱼成为一个较好的选择，此方面的仿生机器鱼[9、10]受到关注.然而这些机器鱼驱动的关键技术和机理有待于进一步研究.

机器鱼鱼尾的摆动所提供的驱动力和外磁场控制这种摆动是该机器鱼设计的关键技术，同时也是本文的主要研究内容.

1 机器鱼驱动控制方程

1.1 鱼尾结构模型

所研究的超磁机器鱼由鱼体和鱼尾组成，鱼尾由贴或镀超磁致伸缩材料的矩形合金薄板构成.由于超磁致伸缩材料具有磁致伸缩特性，即在可变外部磁场作用下，其体积和尺寸会发生相应的改变，故而会对合金薄板产生一种动态荷载分布，由此带动鱼尾产生摆动.

如图1所示，采用笛卡儿坐标系，矩形鱼尾的长为L，宽为b，高为h.且贴或镀的超磁致伸缩材料（图1中黑色部分）厚度ξ（x）（板宽度方向均匀）相对合金薄板更薄，即ξ（x）h.

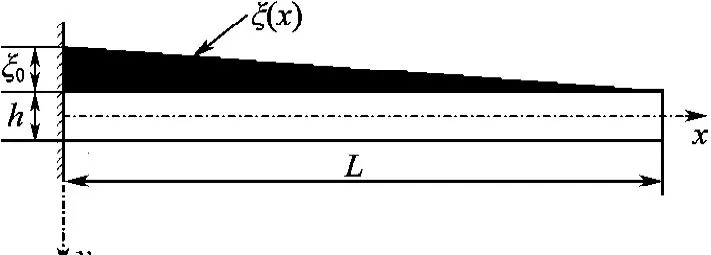
图1 悬臂夹层薄板参数及坐标系Fig.1 Cantilever interlayer plate parameters and coordinates

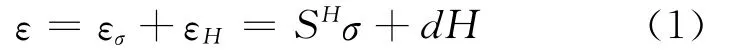
参照Clark的研究成果[11]，超磁致伸缩材料的伸缩与外磁场参数有一定的关系.该本构关系可以表示为其中ε代表总应变；SH为柔顺系数；σ为应力；d为动态磁致伸缩系数；H为外部磁场强度.而由外部磁场引起的应变为

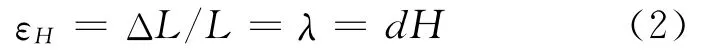
其中λ表示磁致伸缩系数.该材料具有磁性和弹性双重性质，并可以退化为单一材料性质，比如考虑纯弹性材料，令εH＝0且SH＝1/E即可，E为弹性模量.注意到外部磁场强度与磁感应强度B成线性比例关系，即

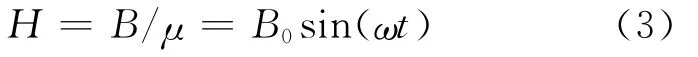
其中B0和ω分别为外部磁感应强度的幅值和磁场频率，μ为磁导率.由于贴或镀在弹性薄板的超磁材料在可变外磁场作用下出现伸缩现象，其对该板的作用可以归结为一种剪切力分布，最终可化为一种弯矩分布如下：

其中A为矩形鱼尾区域面积，E2为超磁材料的弹性模量.由式（4）可注意到超磁贴层厚度直接影响弯矩分布.根据真实鱼类肌肉分布特点，以超磁线性分布作为一阶近似模拟，ξ（x）＝－ξ0（1－x/L）－h/2，这里ξ0为一个常数.弯矩分布可以表示为 关 于x的 二 次 函 数， 即

1.2 鱼尾摆动力学机理

鱼尾由合金板和超磁致伸缩材料组成的夹层薄板构成，是该机器鱼的超磁动力驱动器（GMMA）.为揭示其主要力学行为，忽略超磁致伸缩材料层（ξ（x）h）对该结构弯曲刚度的影响，将驱动鱼尾简化成一个悬臂梁模型，如图1所示.根据微元分析，该模型的振动控制方程可以表示为

其中ρ为合金材料密度，转动惯性矩J＝bh3/12.在力学模型简化过程中，假定鱼尾没有扭转变形，并且鱼尾摆动所受的液体阻力近似与其在流场中产生的阻力相等[12、13].根据 Gerhart等[14]在低雷诺数情况下给出的阻力Fd＝αv∞L（其中α为常数，v∞为无穷远来流速度，L为特征长度），当鱼尾摆动时，其微元上产生的阻力为

其 中v∞＝w（x，t）/t，C为 阻 尼 系 数，C＝μ0π2L/2[ln（2L/b）－0.5＋ln 2]，μ0为液体粘性系数.

依据方程（4）～（6），可以得到鱼尾摆动的控制方程：

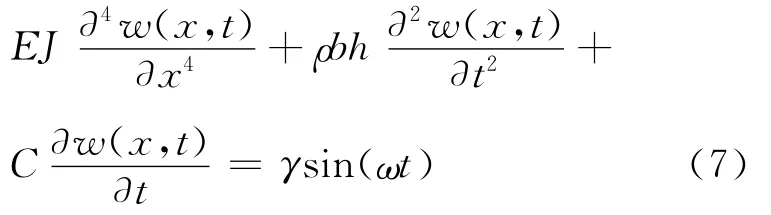
其中γ＝－E1bd B0（ξ0/L）2.模型所对应的边界条件可以写成

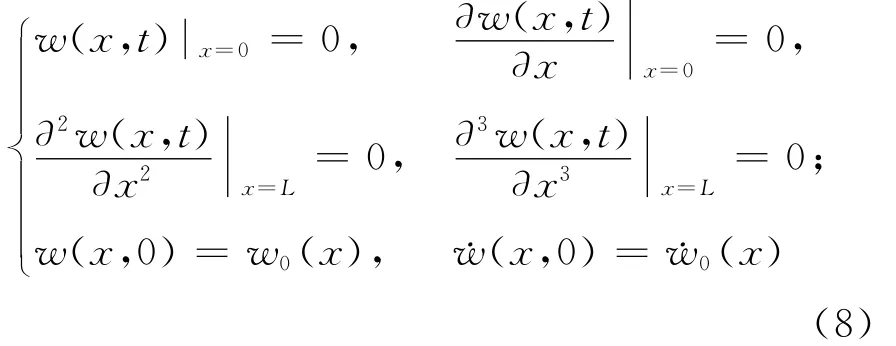
2 控制方程的求解

求解控制方程（7），采用分离变量方法，即

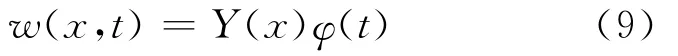
将式（9）代入式（7），则控制方程可以分离成两个独立的常微分方程组[15].

2.1 系统的固有频率[15]

无阻尼系统的自由振动第j阶固有频率可以表示为

相应的振型函数可以表示为

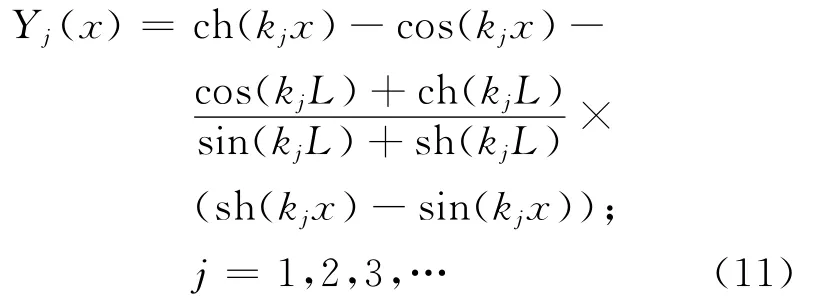
其中k1＝ 1.875/L；k2＝ 4.694/L；kj＝ （2j－1）π/2L，j≥3.

2.2 控制方程求解

依据振型函数的正交性，将控制方程乘以Yj（x），并沿梁长方向积分，则式（12）有如下形式：

通过简化，固有频率式（14）与式（10）是一致的.将控制方程（13）进一步简化，得

在讨论机器鱼稳态游动时，控制方程（15）的稳态通解为

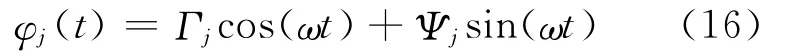
从式（9）、（11）和（16）可以得到鱼尾摆动的横向位移函数表达式.在此若为数值计算不妨取n阶振型叠加，即

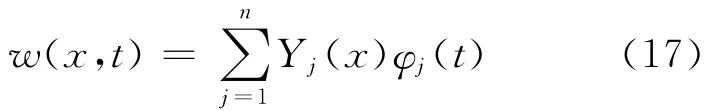
2.3 鱼尾摆动驱动力

鱼尾在可变外磁场控制驱动下，产生相应的摆动，对应的鱼尾摆动横向位移函数随鱼尾轴向位置和时间的变化而变化.在一个外部磁场变化周期内，鱼尾摆动时，其轴向每个微元所受的液体阻力为

因而在一个外部磁场变化周期内，鱼尾摆动产生的平均驱动力可以写成如下形式：

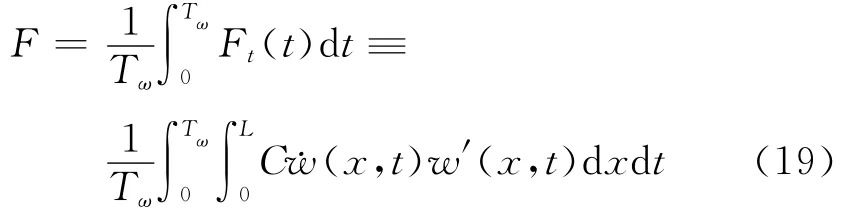
其中Tω＝2π/ω，是外部磁场变化的一个周期.应该指出，机器鱼鱼尾摆动引起的流场对该鱼是有影响的.根据文献[12、13]对振动板附近的流场分析、数值模拟和实验的研究结果，阻尼系数随振动的最大幅值w0降低，此时阻尼系数Cw＝C（1－χw0/L），χ是由实验等确定的参数.因此在计算式（19）时，应该用Cw代替C，这样计算是一个迭代的过程.

2.4 机器鱼游动速度

考虑机器鱼在鱼尾摆动向前游动中，其质心在x方向的位移和速度分别为u和v，v＝u，其运动方程可表示为

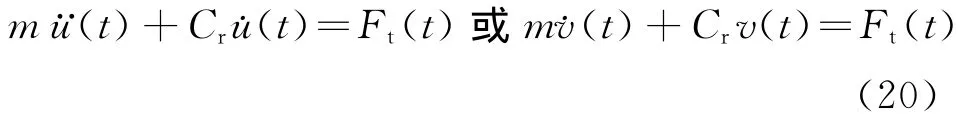
其中m为鱼体质量，Cr为x方向的阻尼系数.讨论机器鱼稳态游动，方程（20）的稳态解，即速度表达式可被解出：

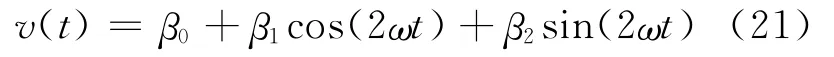
3 数值结果与分析

为了定性和定量地研究该问题，在这里给出一个具体的数值算例，参数选择如下：ξ0＝1.0×10－5m，b＝1.0×10－2m，h＝1.0×10－4m.鱼尾摆动的液体媒介为甘油，它的动力粘性系数μ0＝1.494 Pa·s.合金薄板采用铝合金材料（E＝7.0×1010Pa，ρ＝2.6×103kg/m3），超磁致伸缩材料[11]选择 TbFe2（E1＝9.4×1010Pa，d＝3.77×10－6m/A，B0＝10 T）.采用文献[12、13]的结果，取参数χ＝1.2.鱼尾长度是一个重要的几何参数，它也直接影响系统的固有频率.而外磁场频率接近系统的固有频率时会有特殊的现象.外磁场频率为系统的固有频率时，鱼尾长度与平均驱动力的关系如图2所示.图中Fn（n＝1，2，…，5）曲线代表外磁场频率为系统的n阶固有频率时的情况.从图中可以看出，鱼尾较长时平均驱动力则相当的小.当鱼尾长度选择0.22 m时，一阶固有频率响应的平均驱动力最大为0.15×10－6N；二阶固有频率响应的最佳长度为0.09 m，此时平均驱动力最大为1.53×10－6N；三阶固有频率响应的最佳长度为0.11 m，此时平均驱动力最大为0.28×10－6N；四阶与五阶固有频率响应的最佳长度分别为0.13 m和0.14 m，对应的平均最大驱动力分别为0.61×10－6N和0.25×10－6N.从图中还可以看出在限制鱼尾不太长的情况下，二阶固有频率响应的最佳长度对应的最大驱动力比其他的几个都大.也说明在一般情况下外磁场频率调整为系统的二阶固有频率会达到最佳效果.此外，对于不同的鱼尾长度存在一个最佳的外磁场频率，在此外磁场频率激励下平均驱动力最大.

图2 鱼尾长度与平均驱动力关系Fig.2 Relations between lengths of the fishtail and average propulsions

图3显示出在给定的鱼尾长度下外磁场频率与平均驱动力的关系曲线.图3（a）中5个固有频率分 别 为ω1＝65 Hz，ω2＝407 Hz，ω3＝1141 Hz，ω4＝2236 Hz，ω5＝3696 Hz.图3（b）中5个固有频率分别为ω1＝13 Hz，ω2＝83 Hz，ω3＝231 Hz，ω4＝453 Hz，ω5＝748 Hz.从该图可以看出当外界磁场频率接近系统固有频率时，平均驱动力会出现一个峰值.说明在控制机器鱼游动时应选取接近系统固有频率的外界磁场频率.图3（a）显示二阶固有频率响应的平均驱动力比其他几阶情况都大.并且外界磁场频率为偶数阶固有频率时的平均驱动力要比相邻奇数阶情况要大，这种现象与鱼尾摆动的模态（振型）有关.然而并非所有情况都是如此，图3（b）就给出了不同的结果和现象.由于鱼尾相对长一些，此时四阶固有频率响应的平均驱动力相对最大.但从平均驱动力的数值上看其最大值要比图3（a）最大值小得多.因此图2讨论的最佳鱼尾长度在机器鱼的设计中有着重要意义.

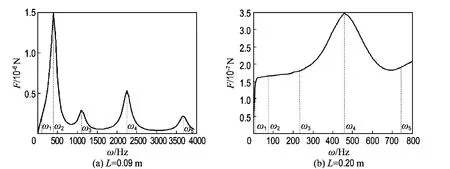
图3 外磁场频率与平均驱动力关系Fig.3 The relationship between the average propulsion and the frequency of the external magnetic fields

图3（a）、（b）中的第二阶和第四阶固有频率响应的平均驱动力是特殊的和关键的点.考察其对应的鱼尾摆动振型（模态）是必要的.图4中W为量纲一位移，图4（a）、（c）给出L＝0.09 m时外界磁场分别在第二阶和第四阶固有频率激励下一个周期内的鱼尾摆动振型.图4（b）、（d）给出L＝0.20 m时相应的情况.从图4（a）、（c）的比较可以看出，随着固有频率阶数的增加对应的振型波数也增加.比较图4（c）、（d），同样都是第四阶固有频率的激励，但振动模态差异很大.在摆动过程中，图4（d）的振型明显有一个向后传播的波，而图4（c）的振型接近于驻波.正是向后传播的波才使得机器鱼向前游动.图4（a）、（b）也有类似现象.图4（a）的鱼尾摆动模态与自然界鱼类巡游模式[16]有同样的规律.

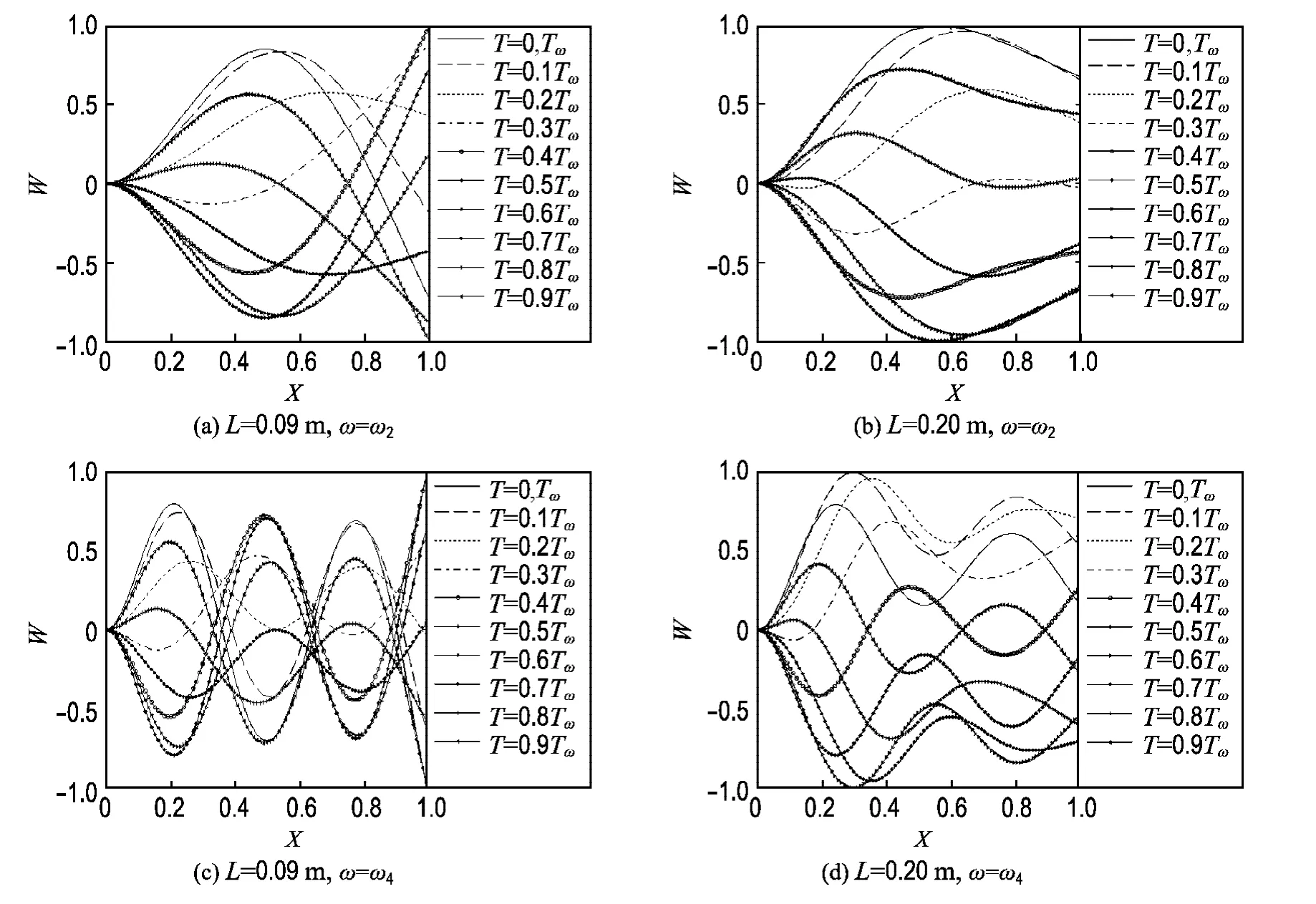
图4 在外界磁场激励下鱼尾模态Fig.4 The modals of the fishtail under the external magnetic fields

为了说明图2中所得到的最佳鱼尾长度，以L为0.07、0.09和0.11 m 为例，在外磁场0～1000 Hz频率段比较和分析其平均驱动力特点，从图5不难看出它们的最大峰值均对应其第二阶固有频率（674、407、273 Hz）.比较它们峰值处的平均驱动力数值大小，知L＝0.09 m的鱼尾驱动力最大.这就说明了比其长或短的鱼尾都不能达到最好的游动效果，再次验证了图2中存在最佳鱼尾长度的结论.对图2中的其他情况计算有类似的规律和结论.

图5 不同鱼尾长度对应的平均驱动力比较Fig.5 Comparison of average propulsions for different lengths of the fishtail

在机器鱼稳态游动中，其尾呈周期性摆动.在这一个周期内，鱼体游动速度是不均匀的并有独特的规律.为说明这种规律，不妨选取参数m/Cr＝4×10－6s和C/Cr＝10－2.由式（21）可得到速度分布.图3的结果表明对于不同的鱼尾长度存在一个最佳的外磁场频率ωopt，在此外磁场频率激励下平均驱动力最大.选取鱼尾长度L为0.05、0.10、0.20和0.30 m，图6（a）给出了其速度分布.从图中可以看出，鱼尾较长时，虽速度分布比较均匀但平均速度较小；鱼尾较短时，幅值较大，快慢不均匀，甚至会出现反向的速度（L＝0.05 m）.综合评价，鱼尾长度为0.10 m 的情况相对理想，其平均速度最大.由此可知鱼尾过长和过短都不利于机器鱼的游动.事实上L＝0.10 m的鱼尾比较接近图2中的最佳鱼尾长度0.09 m.所以在机器鱼的设计中，鱼尾长度是首要问题.当给定了鱼尾长度，外磁场频率也会对一个周期内的速度分布有一定的影响.对照图3（a），取鱼尾长度为0.09 m，考虑图3（a）峰值情况，即特别考虑外磁场频率为固有频率时的特点.图6（b）给出了外磁场频率为前5个固有频率时的速度分布.结果表明对应于高阶固有频率响应的速度分布幅值较小，鱼尾游动较均匀，当然平均速度也小；而对应于低阶固有频率响应的速度幅值较大.从图6（b）还可以看到外磁场在奇数阶（第一、第三和第五阶）固有频率激励下的速度分布中存在反向的速度，这是由对应的振型特征所决定的；外磁场在偶数阶（第二和第四）固有频率激励下的速度分布中就不存在反向速度问题.因此，在机器鱼的设计和控制中应该特别关注这个问题.

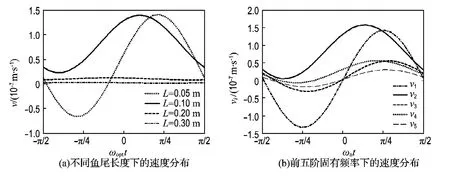
图6 机器鱼稳态游动中的速度分布Fig.6 The velocity distribution in the steady swimming of the robot fish

这里应该指出，在讨论中薄板（鱼尾）的宽度和厚度等是给定的参数，因而最佳的鱼尾长度0.09 m是被计算得到的.若这些参数被调整小一些，则可得到对应的最佳鱼尾长度.这样可以同样设计出小型或微型的超磁机器鱼.

4 结 论

通过外磁场控制超磁机器鱼的游动是可行的.此设计思想避免了携带动力系统，可以实现机器鱼的微型化.在外磁场作用下，机器鱼鱼尾被激励和摆动.鱼尾的摆动模态可以通过调节外部磁场频率来控制.当外磁场频率接近鱼尾系统固有频率时，鱼尾摆动的模态与系统该阶固有频率对应的模态一致，同时所产生的驱动力达到一个较大的峰值.因此，可以通过调整外磁场频率达到超磁机器鱼游动控制的目的.数值结果表明一般情况下系统的二阶固有频率的响应（鱼尾摆动模态）有最佳的工作效率.同时鱼尾长度对机器鱼的游动也有较大的影响.在鱼尾长度增加时，最佳的工作效率会出现在高阶的固有频率响应上.结果说明了各阶摆动模态都存在一个最佳鱼尾长度.这样通过改变鱼尾的长度，也可以调整机器鱼游动的姿态，以适应具体环境.机器鱼在稳态游动时，平均游动速度与平均驱动力成线性比例关系.本文研究结果和结论可为设计同类特种机器人提供借鉴.

[1]OTSUKA A.Development of an eating function support system－especially for severely disabled persons[J].Rigaku Ryoho Journal，1991，25：53－57

[2]CARROZZA M C，LENCIONI L，MAGNANI B，etal.The development of a microrobot system for colonoscopy[J].Lecture Notes in Computer Science，1997，1205：777－788

[3]梅 涛，陈 永，张培强，等.铁磁橡胶执行器与微型游泳机器人的尺度效应[J].光学精密工程，2001，9（6）：523－526

[4]SAOTOME H，OKUBO T，IKEDA Y.A novel actuator with Nd－Fe－B magnets swimming in parallel to the magnetic field [J].IEEE Transactions on Magnetics，2002，38（5）：3009－3011

[5]GUO S X，FUKUDA T，ASAKA K.A new type of fish－like underwater microrobot [J]. IEEE Transactions on Mechatronics，2003，8（1）：136－141

[6]GUO S X，SASAKI Y，FUKUDA T.Development of a novel type of microrobot for biomedical application [J]. Microsystem Technologies，2007，14（3）：307－314

[7]YAMAZAKI A，SENDOH M，ISHIYAMA K，etal.Wireless micro swimming machine with magnetic thin film [J].Journal of Magnetism and Magnetic Materials，2004，272（276）：e1741－e1742

[8]TOMIE M，TAKIGUCHI A，HONDA T，etal.Turning performance of fish－like microrobot driven by external magnetic field [J].IEEE Transactions on Magnetics，2005，41（10）：4015－4017

[9]FUKUDA T， HOSOKAI K， ARAI F. Giant magnetostrictive alloy （GMA）applications to micro mobile robot as a micro actuator without power supply cables [C]// Micro Electro Mechanical Systems， 1991， MEMS ′91， Proceedings. An Investigation of Micro Structures，Sensors，Actuators，Machines and Robots.Nara：IEEE，1991：210－215

[10]张永顺，李海亮，刘 巍，等.超磁致伸缩薄膜尾鳍机器鱼的仿生游动机理[J].机械工程学报，2006，42（2）：37－42

[11]CLARK A E. Ferromagnetic Material [M].Amsterdam：North－Holland Publishing Company，1980

[12]纪亨腾，范 菊，黄祥鹿.垂荡板水动力的数值模拟

[J].上海交通大学学报，2003，37（8）：1266－1270[13]HOLMES S，BHAT S，BEYNET P，etal.Heave plate design with computational fluid dynamics[J].Journal of Offshore Mechanics and Arctic Engineering，2001，123（1）：22－28

[14]GERHART P M，GROSS R J，HOCHSTEIN J I.Fundamentals of Fluid Mechanics[M].2nd ed.New York：Addison－Wesley，1992

[15]张亚辉，林家浩.结构动力学基础[M].大连：大连理工大学出版社，2007

[16]SFAKIOTAKIS M，LANE D M J，DAVIES B C.Review of fish swimming modes for aquatic locomotion [J]. IEEE Journal of Oceanic Engineering，1999，24（2）：237－251