基于FCM聚类的时间序列模糊关联规则挖掘

吕 志 军， 王 照 飞， 谢 福 鼎， 桑 雪

（1.大连理工大学 管理学院，辽宁 大连 116024；2.辽宁师范大学 计算机信息与技术学院，辽宁 大连 116081；3.大连理工大学 计算机科学与技术学院，辽宁 大连 116024）

0 引 言

时间序列是按照时间顺序取得的一系列观察值，它经常出现在诸如经济、商业、工程等领域中.生活中时间序列的数据很多[1、2]，如一个工厂装船货物数量的月度序列、股票每日波动、某化工过程产出的按小时观测值等.在科技期刊出版的评议方面，特别是网络环境下科技期刊的评议方面也可以发现时间序列的数据.如针对某一科技期刊累积5 a的月平均评议数据序列，针对某一篇学术论文1 a中某一时间段的平均评议数据序列等.近年来人们开始对时间序列进行深入的研究，尤其在时态数据的关联规则挖掘方面，做了大量的研究.其中，文献[3]研究了时间序列局部形态的确定性关联问题，文献[4]研究了时间序列形态和后期趋势的关联问题.事实上，时间序列中的形态形式具有不确定性和模糊性，将时间序列形态进行确定性归类和训练是不确切和不合理的，因而有必要引入模糊关联规则的概念.为此，本文提出能使每一个局部序列软化到代表形态中的模糊离散化处理方法，进而研究反映局部形态关联特征的模糊关联规则.

1 时间序列的预处理

1.1 时间序列的分解

用Y表示某个时间序列，该序列可以用下面几个部分表示：

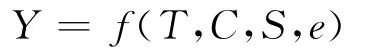
其中T为趋势项，表示长期看时间序列逐渐增加或减少的变化；C为循环项，表示时间超过1 a的周期性变动；S为季节项，表示1 a内的周期性变动；e为随机项，表示不可预期的偶然因素对时间序列的影响.

1.2 时间序列的预处理

时间序列往往受到偶然因素的影响产生随机变化.所以有时使用一些技术方法对数据进行平滑和反季节性处理，以便于更好地发现数据的规律.本文使用的是统计学中的一种时间序列清洗方法[5]，具体步骤如下.

第一步 估计趋势项T，然后得到季节项和误差项的乘积Se＝Y/T；使用中心滑动平均估计趋势项对月度数据使用6个月的中心滑动平均，将数据平滑：

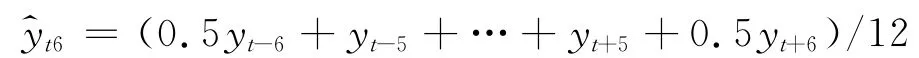
对于季度数据使用2个月中心滑动平均，将数据平滑：

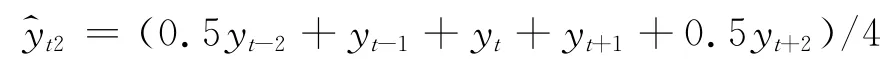
平滑后的数据已经没有季节性

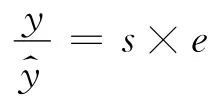
其中s为规范化后的季节因子.

第二步 去掉误差项，估计季节项S，把与不同季节对应的数字称为季节因子，对季节因子进行规范化；去掉长期趋势后的数据y/y＾包括季节和随机误差项.把不同年份相同季节的数据进行平均，就可以去掉误差项.

假设有4 a的月度数据，第一个数据用y1表示，依此类推，所有的数据可以表示为y1，y2，…，y48，用x1，x2，…，x48表示平滑后的数据，为了去掉误差项，把每一年的相同月份求平均：

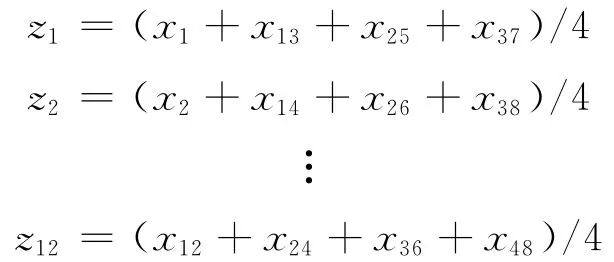
去掉随机误差项后就只剩季节项了，为了保证季节指数的平均数等于1，需要把季节因子规范化：

第三步 从原始数据中去掉季节项，得到经过季节调整的数据.

2 模糊C均值（FCM）聚类算法

1973年，Bezdek提出了模糊C均值（FCM）聚类算法[6]，FCM聚类算法依据每个数据点的隶属度来确定其属于某个类的程度.它首先将n个样本点xi（i＝1，2，…，n）划分为c个模糊类，然后求出每个模糊类的聚类中心，使得相似性价值函数达到最大，其中，每个样本点的隶属度取值范围为[0，1]，即隶属矩阵U的元素取值在[0，1]上.根据归一化原则，数据集隶属度的总和等于1：

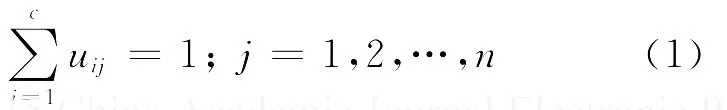
那么，FCM的价值目标函数被定义如下：

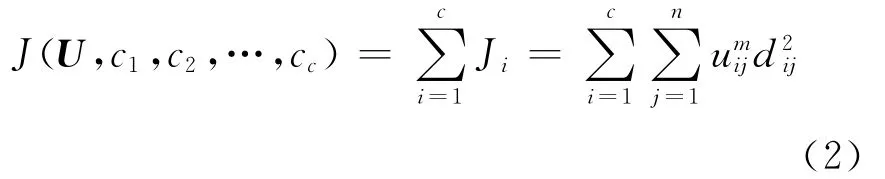
其中Ji为组i内的价值函数；uij∈[0，1]指第j个样本点属于第i个模糊类的程度；ci是第i个模糊类的聚类中心；dij＝‖ci－xj‖，指聚类中心ci与样本点xj之间的欧几里德距离；m∈ [1，∞），为加权指数.

若使得式（2）达到最小值，则必要条件为

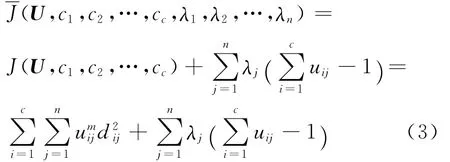
其中λj为式（1）中n个约束的拉格朗日乘子，j＝1，2，…，n.将所有输入参量求导，最小化式（2）的必要条件为

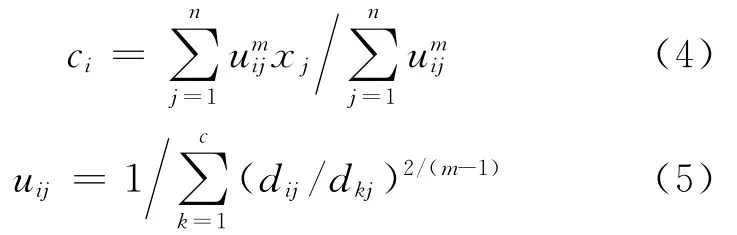
通过批处理方式，FCM以4个步骤确定聚类中心ci和隶属矩阵U：

步骤1 初始化隶属矩阵U，U中元素取为[0，1]的随机数，使其满足式（2）中的约束条件.

步骤2 根据式（4）计算聚类中心ci，i＝1，2，…，c.

步骤3 根据式（2）计算目标函数.若函数值小于预先定义的阈值，或相对上次目标函数的变化量大于预先定义的阈值，则算法中止.

步骤4 根据式（5）更新矩阵U作为新的隶属矩阵.返回步骤2.

对于一长度为n的时间序列按1.2中的预处理方法进行处理后，将其采用FCM聚类算法划分属性.

把每月相对于平均趋势的波动情况作为新的时间序列来替代原时间序列，而后对其使用上述方法进行模糊聚类，将其中的每一个局部序列软化到代表形态.

设X＝ ｛X1，X2，…，Xn｝为新时间序列，将一宽度为w的时间窗作用于X，形成一长度为w的子序列Yi＝ ｛Xi，Xi＋1，…，Xi＋w－1｝，将时间窗在时间序列X上从始点至终点进行单步滑移，形成一系列宽度为w的子序列M1，M2，…，MN－w＋1，记W（X，w）＝｛Mi｜i＝1，2，…，N－w＋1｝为由该时间序列X用宽度为w的滑窗移动出的子序列集合，将W（X，w）看做w维欧氏空间中的（N－w＋1）个点，然后用FCM方法进行聚类.

3 关联规则的并行挖掘

Apriori算法[7]是最著名的关联规则算法，已经为大部分商业产品所采用.目前，基于Apriori已经提出了若干种发现频繁属性集的并行算法.算法将候选项集并行化，对其进行划分并在每个处理器上分别计数，各处理器之间通过消息传递进行通信.计数分配（CD）是著名的关联规则并行算法，每个处理器对本地数据的候选进行计数，并将这些计数传播到所有其他处理器上.然后每个处理器进行全局计数，这些全局计数用于确定大项目集并生成下趟扫描时的候选.CD算法具有好的规模增长性、可扩展性和加速比性能.

利用并行算法处理后得到时间序列，对连续属性进行离散化，得到新的模糊属性数据集，将其划分在每个处理器上.本文设计了一个新的关联规则并行挖掘算法，采用SPMD模式，各处理器之间只交换本地模糊支持数，不进行数据交换.在数据扫描过程中，处理器可以异步、独立地计算本地模糊支持数.每次扫描结束时保持同步，并且所有处理器保存相同的候选集.下面是模糊关联规则并行挖掘算法.

输入：最小模糊支持度minSup；最小模糊信任度minConf

输出：关联规则集Sar

步骤1 设置并行处理器p1，p2，…，pn.

步骤2 将事务数据库划分为多个分区，并分别分配到每个处理器上.

步骤3 对每个处理器，采用FCM算法进行聚类，将其转化为新的数据集，结合连续属性离散化技术将得到的时间序列转换为新数据库，并根据最小模糊支持度minSup和最小模糊信任度minConf构建前缀树.

步骤4 依据步骤3在每个处理器上进行局部计数；对于事务数据库中的每个事务和候选项目集中的每个项目，如果某个项目属于某个处理器上的事务，则进行局部计数，并将它们传播到其他站点.

步骤5 计算全局计数，生成规则集.

4 实 验

本文的实验数据是1992－01至2008－12美国洛杉矶闹市区臭氧每月平均记录.表1为将数据统计记录按一年12个月进行分段后得到的数据.

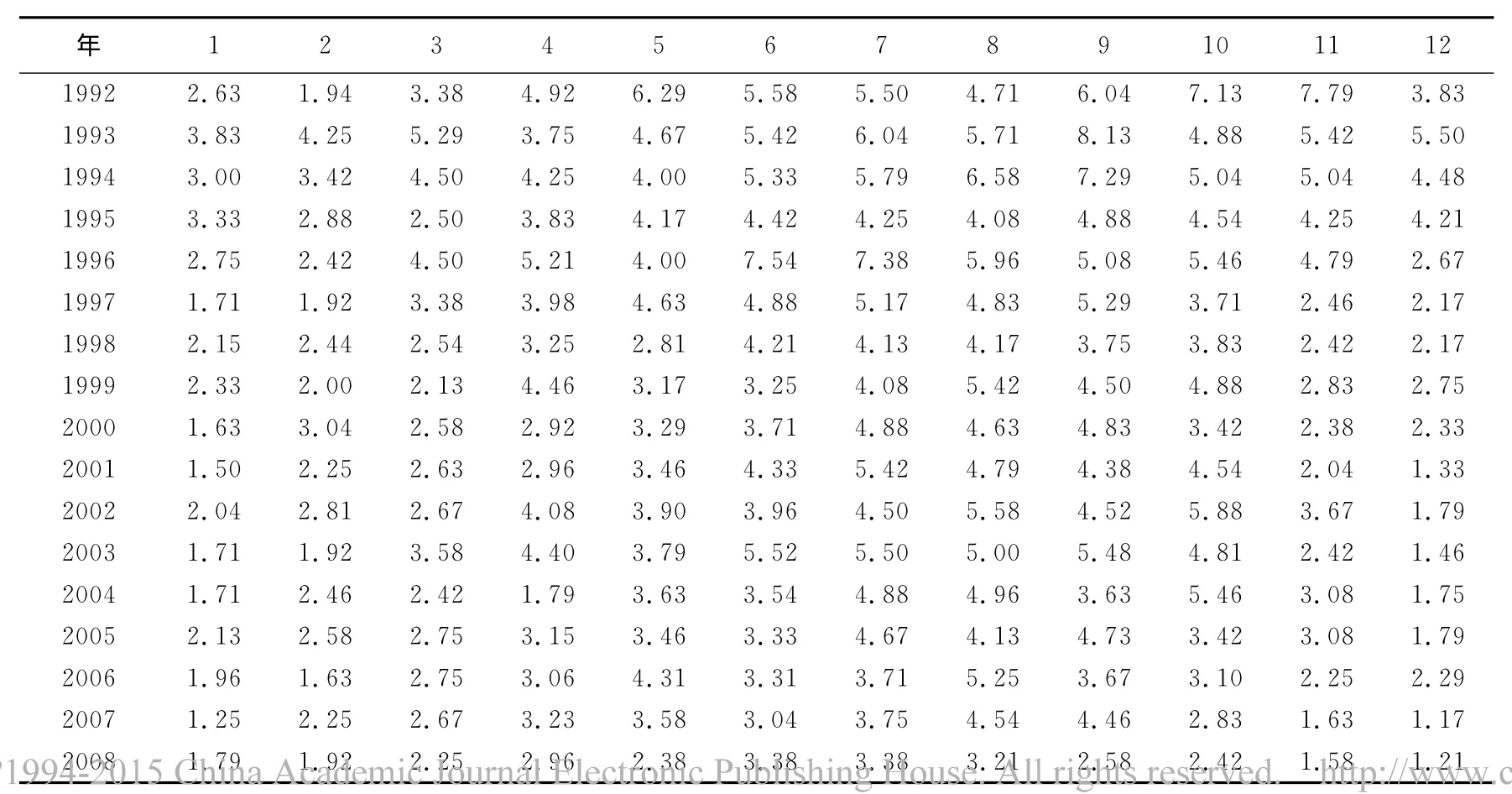
表1 洛杉矶闹市区臭氧每月时均记录Tab.1 Monthly averages of hourly readings of ozone in downtown Los Angeles

通过公式计算，得到每月相对于平均趋势的波动情况（见表2）.

本文的关联规则是在滑窗参数w（w＝3）、聚类类数（类数＝4）固定的条件下进行的.首先产生了A、B、C、D4种代表形态，如图1所示.

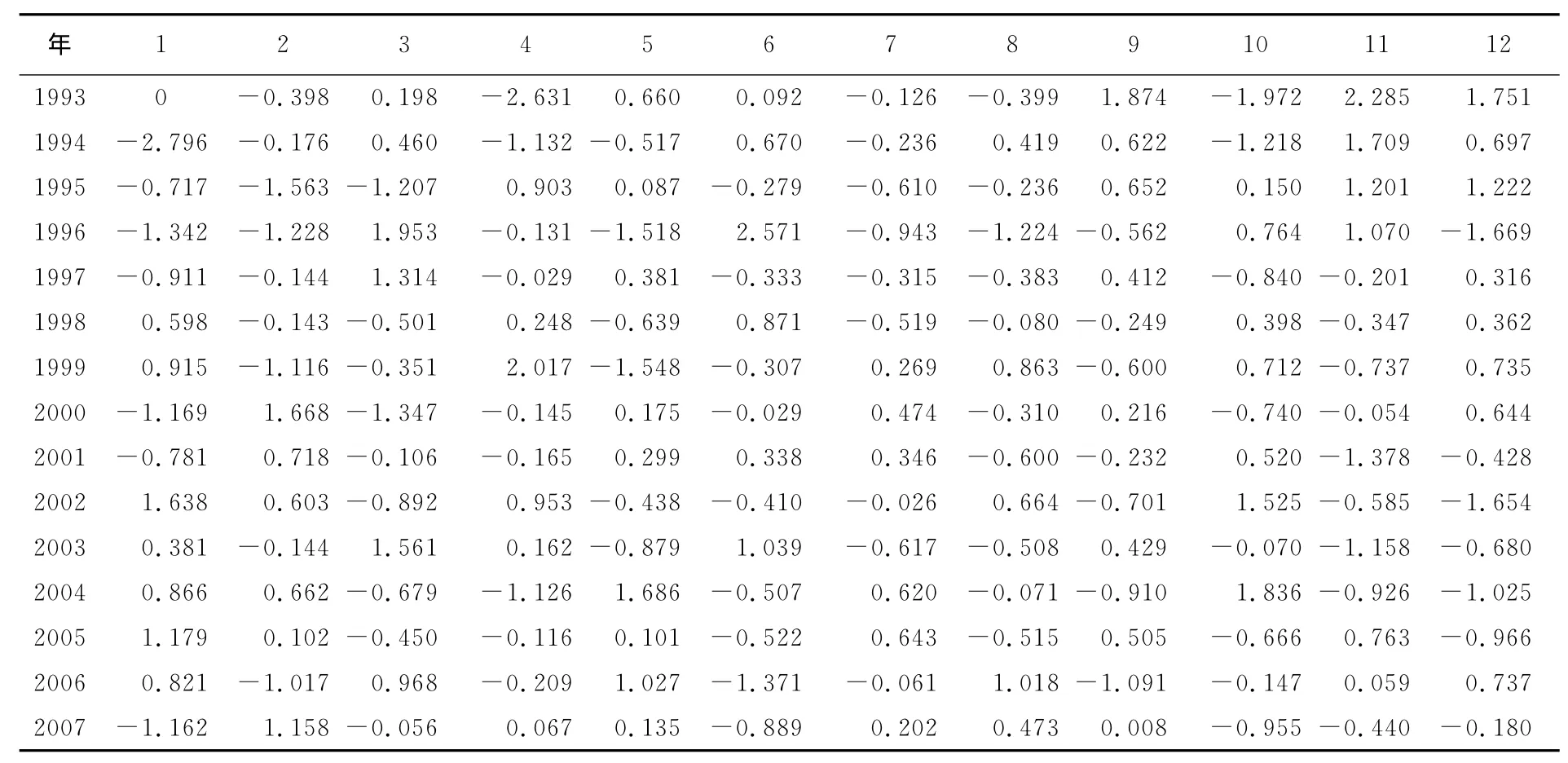
表2 相对于平均趋势的波动情况Tab.2 The fluctuations compared with the average trend %

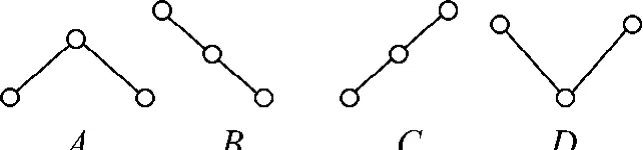
图1 波动关联规则的4种形态Fig.1 Four patterns of fluctuated association rules

再通过本文提出的算法对其进行规则的挖掘[8]，所得的模糊关联规则集如下：

支持度13.33%，置信度50%时，有

（1）2B＼3C＝＞7B＼9A

（2）7C＼8A＝＞10C＼12B

支持度13.33%，置信度67%时，有

（3）1C＼2A＝＞7C＼9D

（4）2A＼3D＝＞8A＼9D

（5）4D＼5A＝＞7C＼8C

（6）5D＼6A＝＞7D＼8A＼9D

（7）1B＼3A＝＞4B＼6C

（8）2A＼3B＝＞4D＼5A＼6B

（9）2A＼3D＝＞4A＼5B＼6B

支持度13.33%，置信度100%时，有

（10）8D＼9A＝＞10B＼11C＼12A

（11）4A＼5B＼6B＝＞7C＼8A＼9D

（12）4D＼5A＼6B＝＞10B＼12C

（13）1B＼2B＝＞5D＼6A

（14）8C＼9A＝＞10D＼11C＼12A

得到以上规则集后，对于2007年以后出现的新数据，通过本文所给出的方法进行反季节化处理和模糊离散化处理后，就可以对未发生的事件进行模糊形态估测.虽然2008年下半年的数据已经发生，但为便于实验，这里假定并未发生，采用上述方法进行了预测，预测结果与真实事件形态基本符合，证明了本文方法的有效性.

5 结 语

本文提出了基于FCM聚类的时间序列模糊关联规则挖掘算法.此挖掘算法首先采用FCM聚类算法对清洗后的时间数据进行模糊离散化处理，将每一个局部序列软化到代表形态中.采用改进的关联规则并行挖掘算法以发现频繁模糊属性集，最后由多个处理器并行地产生满足最小模糊信任度的模糊关联规则.实验证明，该并行算法具有好的可扩展性、规模增长性和加速比性能.

[1]GAO L，WANG X Y S.Continuous similarity－based queries on streaming time series [J]. IEEE Transactions on Knowledge and Data Engineering，2005，17（10）：1320－1332

[2]ZHANG Z G，CHAN Shing－chow.Robust adaptive Lomb periodogram for time－frequency analysis of signals with sinusoidal and transient components[C]//IEEE ICASSP.Philadelphia：IEEE，2005：493－496

[3]DAS G，LIN King－ip，MANNILA H，etal.Rule discovery from time series[C]//Proceeding of the 3rdInternational Conference of Knowledge Discovery and Data Mining.California：AAAI Press，1998：16－22

[4]MARK L，KLEIN Y，KANDEL A.Knowledge discovery in time series databases [J].IEEE Transactions on Systems，Man and Cybernetics，2001，31（1）：160－169

[5]GEORGE E P B，JENKINS G M，REINSEL G C，etal.时间序列分析预测与控制[M].顾 岚，等译.北京：中国统计出版社，1997

[6]高新波.模糊聚类分析及其应用[M].西安：西安电子科技大学出版社，2004

[7]AGRAWAL R，SHAFER J C.Parallel mining of association rules：design， implementation and experience[J].IEEE Transactions on Knowledge and Data Engineering，1996，8（6）：962－969

[8]TAN Pang－ning，STEINBACH M，KUMA V.数据挖掘导论[M].范 明，范宏建，等译.北京：人民邮电出版社，2006