一种基于局部特征的网络节点重要性度量方法

王 建 伟， 荣 莉 莉， 郭 天 柱

（大连理工大学 系统工程研究所，辽宁 大连 116024）

0 引 言

现实生活中的许多系统都可以通过网络的形式加以描述，如人际关系网络[1]、航空网络[2]、电力网络[3]、互联网络[4]、新陈代谢网络[5]、科研合作网络[6]等.近年来随着大规模网络实证研究的开展，对于哪些节点在网络功能运转中扮演重要角色的研究引起了国内外学者的广泛关注，并出现了许多结合不同实际背景的节点重要性评估方法[7～9].这些方法都基于节点之间的差异性，从某一角度探讨网络节点的重要性问题，如人际关系网络中节点本身的地位；通讯网络中节点对信息传播的控制能力；交通网络中节点处理信息的流量等.大体可以将这些方法分为三大类：节点关联性问题、最短路径问题和网络流问题，具体包括度、介数[10、11]、凝聚性[9]、特征向量[8]、子图[12]、网络流[13]、随机行走[14]等.其中基于度的重要性评估方法最为简单，它只强调节点与邻接节点连边的数量；介数刻画了节点或边对网络中信息或流的控制能力；凝聚性侧重于分析节点在网络中的几何位置；特征向量充分考虑与目标节点建立连接节点的重要性，并通过邻接节点的重要性来确定目标节点的地位；子图反映了节点在网络局部结构的贡献大小；网络流和随机行走都利用模拟现实的思想，分析网络节点在实际应用中的作用.

此外，网络节点重要性评估方法研究还有谭跃进等[15]提出的节点收缩方法，李翔鹏等[16]和许进等[17]提出的核与核度理论.前者与前面介绍的方法一样，从节点对网络的贡献出发评估其重要性；后者则采用了节点删除法的思想，用节点删除后对网络连通性破坏程度定义其重要性.

上述节点重要性评估方法的差异主要体现在对节点重要性的定义上，无论是基于节点显著性等价于重要性，还是破坏性等价于重要性，都需要给重要性一个合适的定义和度量方法.在现有的评估方法中，对网络节点重要性的度量都是侧重于全局和局域两个不同的角度.而基于全局的角度对网络中节点重要性的度量需要遍历整个网络，例如，节点介数的计算都要遍历整个网络，这在小规模的网络中具有一定的应用价值，但现实生活中的很多网络，网络规模非常庞大，结构非常复杂，想从全局的角度度量节点的重要性几乎是不可能的；网络流的方法既耗资源，又不太现实；而一些基于局域角度的度量方法，譬如：度方法不能很好地描述出节点之间的差异性，节点收缩方法又不能很好地体现研究节点本身的度的情况.鉴于此，基于节点度和邻居节点度，本文提出一种简单而有效的网络节点重要性的度量方法，即节点的度，节点的邻居节点的度越大，节点就越重要.这样一方面克服了全局方面应用的局限，又在一定程度上使得网络中心节点的判别方法得到简化，可以使得在效率、有效性等方面更优于已有的方法.

1 符号与方法的描述

1.1 网络的表示

网络可以用二元组（V，E）表示，其中V＝｛v1，v2，…，v n｝，代 表 节 点 集 合，E＝ ｛e1，e2，…，em｝，代表边的集合，n和m分别表示网络包含的节点数和边数.网络的邻接矩阵A为

其中aij∈ ｛0，1｝，i，j＝1，2，…，n，表示节点i与节点j之间是否有边相连，如果aij＝1，则表示节点i与节点j之间有边，否则表示节点i与节点j之间没有边.

1.2 方法描述

网络中节点的重要性与节点所连边的重要性是密切相关的.

公理1 连接节点的边越重要，节点越重要.

基于公理1，将从网络边的角度来探讨节点的重要性.设w ij表示边ij的权重，同时节点i的所有邻居节点表示为Гi.

定义1 边ij的权重定义为

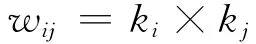
其中ki表示与节点i连接的边的数目，即节点i的度.令

其中e＝（111 … 1）T是n维列向量；b＝（b1b2…bn）T，bi表示为节点i的度.所以，边ij的权重可以表示为

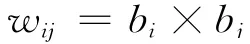
定义2 带有边权的节点i的权重定义为w i表示节点i所连边的权值之和.

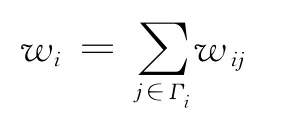
由定义2可以看出，节点i的重要度取决于节点i所连边的权值的大小，而边的权值有两个影响因素：一是节点i的度k i，另一个是节点i的邻居节点的度.相同条件下，如果节点i的度k i越大，同时所对应的邻居节点的度越大，该节点越重要.

定义3 为消除网络规模对节点权重的影响，定义归一化的节点i的重要性为

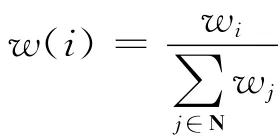
1.3 方法优势分析

图1描述了网络节点重要性与节点的度及节点邻居节点连接状况之间的密切关系.

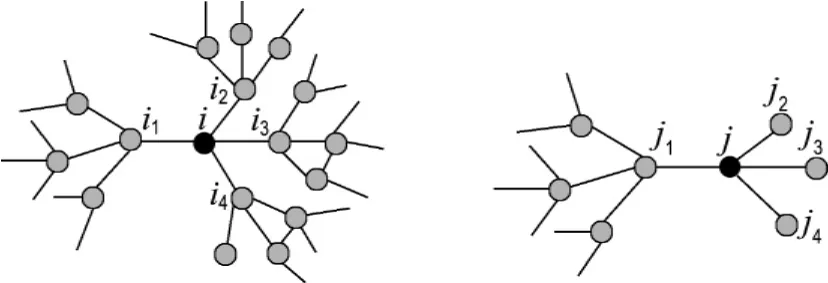
图1 局部特征方法的优势Fig.1 Advantages of local characteristics method

在图1中，很明显，节点i和j的局部特征影响了两个节点在网络上的重要性.在网络的拓扑结构上，虽然两个不同节点具有相同的度，然而由于邻居节点的影响，节点i的重要性明显高于节点j的重要性.可以看出，节点本身的度及其邻居节点特征都是不能够忽略的指标.由于考虑到了网络节点的局部特征，本方法对于度分布较为异质的网络，如具有无标度特性的网络：Internet、人际关系网络、科研合作网络、新陈代谢网络、引文网络以及电子邮件网络等，都能够比较细致地凸现节点之间的差异性，并比较客观地反映节点对网络整体的影响效应.

2 实例分析

选取艾滋病患者性关系网络作为研究对象，如图2所示.网络中节点表示带有艾滋病的患者，边表示两个艾滋病患者之间存在性关系.

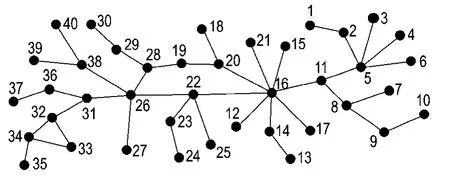
图2 艾滋病患者性关系网络[18]Fig.2 Sexy relation network of the patients with AIDS[18]

2.1 方法对比

分别用本文提出的方法、度方法、凝聚性方法、介数方法以及节点删除法对艾滋病患者性关系网络中节点的重要性进行评估，计算结果如表1所示.

在图2中，可以看到仅仅通过节点度并不能够很好地区别不同节点对网络整体的影响，例如，节点8、11、20和38尽管都拥有相同的度3，但由于所连接的邻居节点之间度的差异对它们的影响，4个节点在网络中所起的作用显然不同.实验结果表明基于局域角度的网络节点重要性的度量方法能更细致地刻画网络中节点之间的差异性.

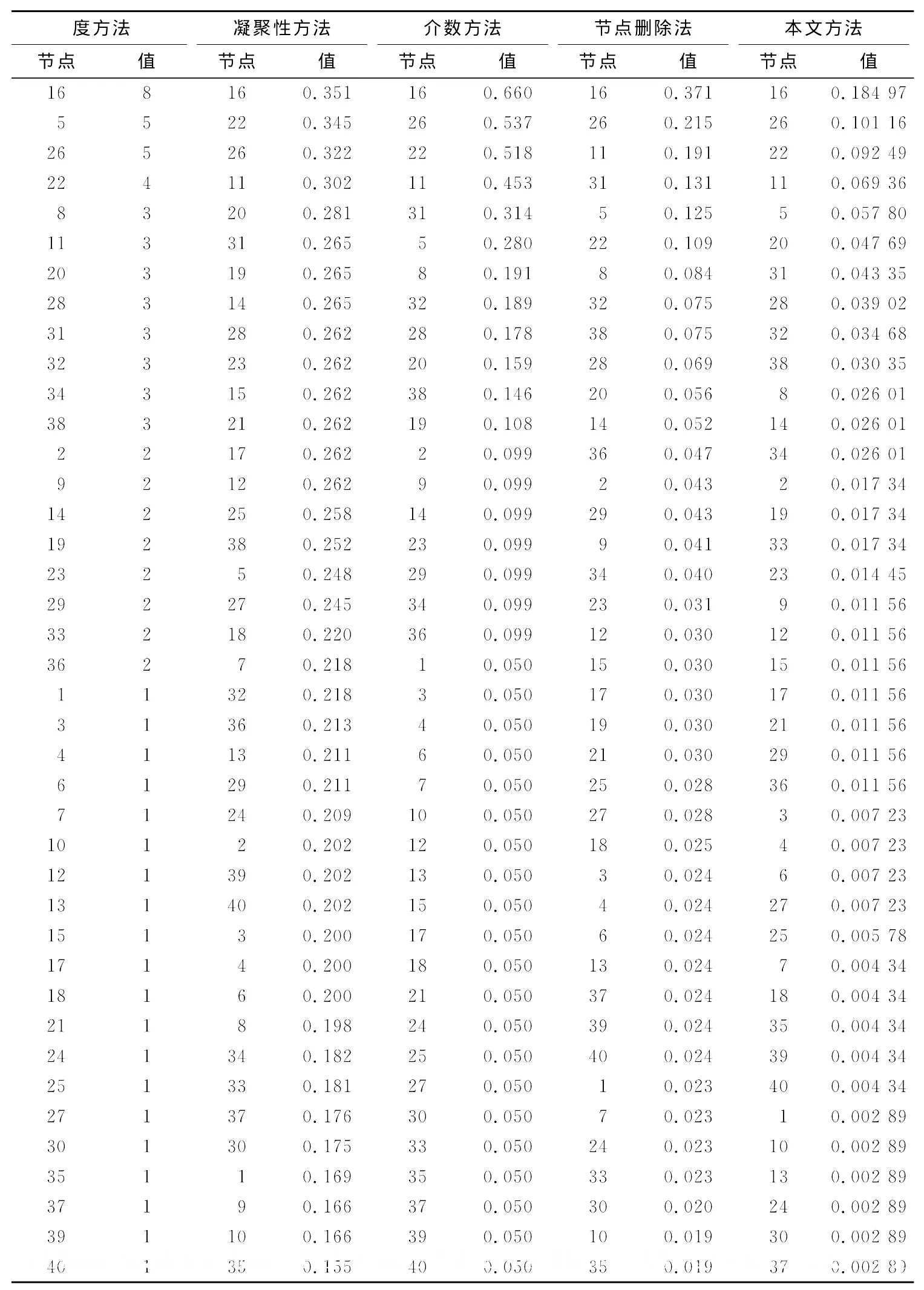
表1 节点重要性评估结果Tab.1 Valuable results of node importance

不同的指标是从不同的角度来探讨同一问题的，所以指标无所谓好坏，每个指标都有自身的优点和缺点，如节点度注重节点在局部的影响，而无法体现节点在网络中的整体作用；凝聚性强调节点对整个网络广播消息需要的总花费，而忽视了信息传播过程中的覆盖率等.本文提出的节点重要性的度量方法，从网络的局部特征入手，不仅能充分体现节点本身的影响力，而且也全面地考虑了节点的邻居对节点本身的间接影响效应，这在人际关系网络、渠道销售网络、传染病网络等许多实际网络中，在无法获得网络的全局信息和网络规模庞大的情况下，应用本文所提出的方法更符合事实，对实际应用有指导意义.

2.2 时间复杂度对比分析

几乎所有的复杂系统都可以抽象成网络模型，这些网络往往具有大量的节点，网络规模庞大，这使得在实际的情况下，考虑度量网络节点的重要性方法的同时，也不得不关注算法的时间复杂度，关注对大型的复杂网络应用此类方法能不能获得理想的计算能力.

本文对比了几类典型的网络节点重要性的评估方法，如表2所示.

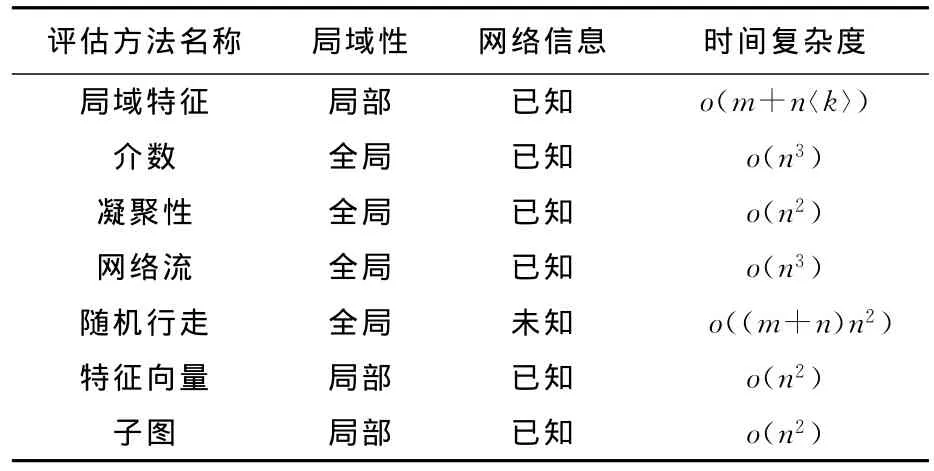
表2 时间复杂度对比Tab.2 Comparison of time complexity

方法的时间复杂度对比分析中，n为网络的规模，m为网络的边数目.从方法的时间复杂度对比中可以看到，本文提出的评估节点重要性的局部特征方法的时间复杂度仅为o（m＋n〈k〉），明显低于介数、凝聚性、网络流、随机行走、特征向量和子图等评估方法.而且，各方法对网络中节点评估的对比，也说明了此方法的有效性.在现实的绝大多数网络中，如Internet、WWW、电子邮件网络等，网络规模庞大，网络拓扑结构复杂，因此，急需一种简单、计算时间复杂度小，同时又有效的方法对网络节点重要性进行评估.而局域特征方法一方面克服了全局法应用的局限，又在一定程度上使网络中心节点的判别方法得以简化，计算的时间复杂度仅线性相关于网络的规模，因此可以使得在效率、方法的有效性等方面更优于已有的方法.本方法对于大型的复杂网络可以获得更理想的计算速度.

3 结论与展望

通过本文提出的方法与其他几种典型的节点重要性评估的方法结果的对比、算法的时间复杂度的分析，认为新方法具有以下优点：

（1）依据网络局部特征来评判网络中节点的重要性，避免了对网络全局架构的了解；

（2）方法简单有效，只考虑了所关注节点本身的度及其邻居节点的度的情况，在现实生活中，很容易获得数据；

（3）算法的时间复杂度很小，对于大型的网络而言是一个比较优越的算法.

从方法的对比中可以发现，本文所提出的方法与介数存在一定的关联性，如前面的几个重要节点序列是一致的，然而在某些节点上也存在很大的分歧，如节点33，虽然不同的方法考虑问题的角度不同，但是本文所提出的方法与节点的介数方法间的相似性，绝不是偶然.如果能够从网络的局域角度获得一种方法，并能够很好地代替介数方法，这样就有效地避免了介数方法存在的两个缺陷：一是要了解网络的全局信息，二是算法的高时间复杂度.寻找一种有效的方法更好地拟合介数方法，这将在实际的网络应用中具有更大的价值.

[1]NEWMAN M E J.The structure and function of complex networks[J].SIAM Review，2003，45（2）：167－256

[2]GUIMERA R，AMARAL L A N.Modeling the world－wide airport network [J]. The European Physical Journal B，2004，38（2）：381－385

[3]KINNEY R，CRUCITTI P，ALBERT R，etal.Modeling cascading failures in the North American power grid [J].The European Physical Journal B，2005，46（1）：101－107

[4]FALOUTSOS M，FALOUTSOS P，FALOUTSOS C. On power－law relationships of the internet topology [J].Computer Communications Review，1999，29（4）：251－262

[5]JEONG H，MASON S，BARABSI A L，etal.The large－scale organization of metabolic networks [J].Nature，2000，407（6804）：651－654

[6]NEWMAN M E J.The structure of scientific collaboration networks [J]. Proceedings of the National Academy of Sciences，2001，98（2）：404－409

[7]FREEMAN C L.A set of measures of centrality based on betweenness[J].Sociometry，1977，40（1）：35－41

[8]FREEMAN C L.Centrality in social networks：I.Conceptual clarication [J].Social Networks，1979，1（3）：215－239

[9]FREEMAN L C，ROEDER D，MULHOLLAND R R.Centrality in social networks：ii.Experimental results[J].Social Networks，1979，2（2）：119－141

[10]BARTHELEMY M.Betweenness centrality in large complex networks [J]. The European Physical Journal B，2004，38（2）：163－168

[11]GOH K I，OH E，KAHNG B，etal.Betweenness centrality correlation in social networks [J].Physical Review E－Statistical，Nonlinear，and Soft Matter Physics，2003，67（1）：017101－1－017101－4

[12]ESTRADA E，RODRGUEZ－VELZQUEZ J A.Subgraph centrality in complex networks [J].Physical Review E－Statistical，Nonlinear，and Soft Matter Physics，2005，71（5）：056103－1－056103－9

[13]PERRA N，FORTUNATO S.Spectral centrality measures in complex networks[J].Physical Review E－Statistical，Nonlinear，and Soft Matter Physics，2008，78（3）：036107－1－036107－10

[14]NEWMAN M E J.A measure of betweenness centrality based on random walk [J]. Social Networks，2005，27（1）：39－54

[15]谭跃进，吴 俊，邓宏伟.复杂网络中节点重要度评估的节点收缩方法[J].系统工程理论与实践，2006，26（11）：79－83

[16]李翔鹏，任玉晴，席酉民.网络节点（集）重要性的一种度量指标[J].系统工程，2004，22（4）：13－20

[17]许 进，席酉民，汪应洛.系统的核与核度理论[J].系统科学与数学，1993，13（2）：102－110

[18]KLOVDAHL A S.Socail networks and the spread of infectious diseases：the AIDS example[J].Social Science Methods，1985，21（11）：1203－1216