最大当量排队长度模型及其时空特性

姚 荣 涵， 王 殿 海

（1.大连理工大学 交通运输学院，辽宁 大连 116024；2.浙江大学 建筑工程学院，浙江 杭州 310058）

0 引 言

交通运输系统中存在很多排队现象，最大排队长度是车辆排队过程中的一个临界值[1].针对最大排队长度的研究并不多见.国外，有学者提出最大排队长度的解析表达式[2]；探讨无信号交叉口排队长度的分布[3]；还有学者针对无信号交叉口提出一种估计最大排队长度的宏观动态模型[4].国内，一些学者根据准冲击波方法或交通波理论计算信号交叉口红灯末或高速道路交通事故发生后车辆的最大排队长度[5～7].这些研究成果主要是求解了最大排队长度的数学期望.

在信号交叉口，红灯期间车辆形成排队，红灯末排队长度达到最大值，此刻是单个路段排队现象最为严重的时刻，同时也是车辆排队可能在路网中引起连锁反应的关键时刻.揭示这一最大排队长度的时空特性对探讨交通多米诺效应有重要意义.本文基于单车道路段当量排队长度模型建立最大当量排队长度（即红灯末当量排队长度）模型，并据此分析最大当量排队长度的时空特性.

1 模型建立

根据二流理论[8]，单车道路段当量排队长度模型为[9]

式中：Ld（t）为时刻t上、下游断面间的当量排队长度；N0为初始时刻t＝0上、下游断面间的车辆数；Nu（t）和Nd（t）为时刻t累计通过上、下游断面的车辆数；L为上、下游断面间的距离；km和kj为上、下游断面间交通流的最佳密度和阻塞密度.

假设时刻t对应于第j个采样周期末，则时刻t累计通过上、下游断面的车辆数为

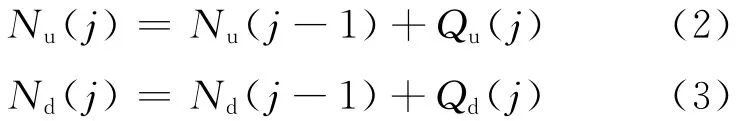
式中：Nu（j）和Nu（j－1）为第j和j－1个采样周期末累计通过上游断面的车辆数；Qu（j）和Qd（j）为第j个采样周期内通过上、下游断面的车辆数；Nd（j）和Nd（j－1）为第j和j－1个采样周期末累计通过下游断面的车辆数.

式（2）和（3）中j＝1，2，3，…；当j＝1时，Nu（0）＝0，Nd（0）＝0，即上、下游断面初始累计车辆数均为0.

将式（2）、（3）代入式（1），则

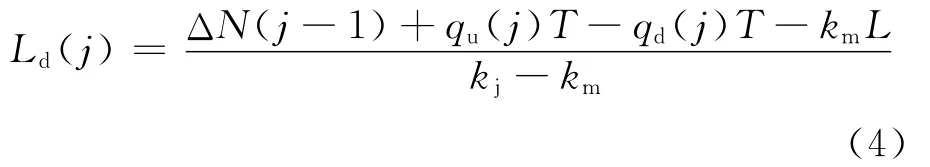
式中

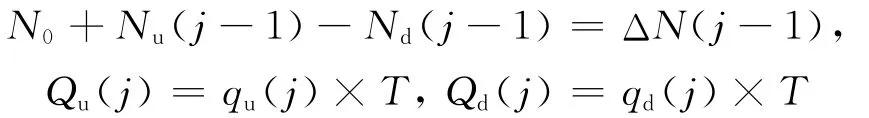
ΔN（j－1）为第j－1个采样周期末上、下游断面间的车辆数；qu（j）和qd（j）为第j个采样周期内通过上、下游断面的车流量；T为采样间隔.

在信号交叉口绿灯期间车辆处于释放过程中，从绿灯开始到绿灯结束，排队长度随着时间推移不断变短；红灯期间车辆在交叉口停车线前依次排队，从红灯开始到红灯结束，排队长度随着时间推移不断变长.在信号控制系统中，往往需要控制最大排队长度，因此预测最大当量排队长度也具有重要意义.下面来建立最大当量排队长度模型.

红灯开始时，到达停车线的车辆必须停车，此后来车必须依次排队.因而，红灯期间通过下游段面的车辆数为0，即qd（j）＝0，则式（4）简化为

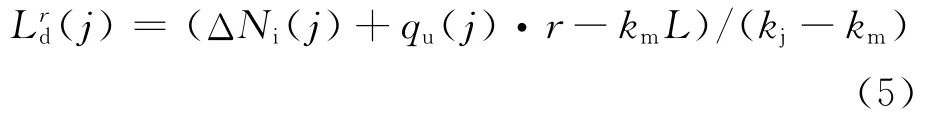
式中：（j）为第j个红灯末的当量排队长度，即最大当量排队长度；ΔNi（j）为第j个红灯初的滞留车辆数；qu（j）为第j个红灯期间即采样周期内上游到达的车流量；r为红灯时长.

根据信号配时理论可知[1]

式中：C为周期时长；u为绿信比.

假定红灯期间上游到达车流量为q，简写ΔNi（j）为N，将式（6）代入式（5）得

式中：为最大当量排队长度；N为红灯初滞留车辆数；q为红灯期间到达车流量.

2 时空特性

2.1 交通流特性

当N、C、u、L一定，最大当量排队长度与到达车流量的函数关系为

从式（8）来看，当N、C、u、L一定与q呈线性关系，见图1.直线斜率由周期时长和绿信比决定，截距由滞留车辆数和路段长度决定.周期越长，绿信比越小，斜率越大；滞留车辆数越多，路段越短，截距越大.

由图1（a）可见，当C、u、L一定，不同N形成的Lrd－q曲线族为一系列平行直线，直线斜率相同，滞留车辆数越多，截距越大；无论q取何值，同一q对应的相同ΔN均引起相同的ΔLrd，反之亦然；这说明此时L rd对q和N均不敏感.由图1（b）可见，当N、u、L一定，不同C形成的L rd－q曲线族为一系列不平行直线，直线截距相同，周期越长，斜率越大，随着q增大，直线族由收敛变得发散；周期越长，同一Δq引起的ΔLrd越大，这说明最大当量排队长度对周期较敏感；到达车流量越大，同一ΔC引起的ΔLrd越大，这说明最大当量排队长度在流量低时对周期不敏感，在流量高时敏感，流量越大，越敏感.由图1（c）可见，当C、N、L一定，不同u形成的L rd－q曲线族为一系列不平行直线，直线截距相同，绿信比越大，斜率越小，随着q增大，直线族由收敛变得发散；绿信比越小，同一Δq引起的ΔLrd越大，这说明最大当量排队长度对绿信比较敏感；到达车流量越大，同一Δu引起的ΔLrd越大，这说明最大当量排队长度在流量低时对绿信比不敏感，在流量高时敏感，流量越大，越敏感.由图1（d）可见，当C、u、N一定，不同L形成的Lrd－q曲线族为一系列平行直线，直线斜率相同，路段越长，截距越小；无论q取何值，同一q对应的相同ΔL均引起相同的ΔLrd，反之亦然；这说明此时Lrd对q和L均不敏感.

当q、C、u、L一定，最大当量排队长度与滞留车辆数的函数关系为

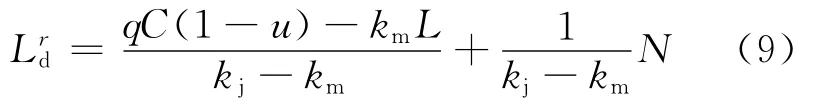
从式（9）来看，当q、C、u、L一定，Lrd与N呈线性关系，见图2.直线斜率是常数，截距由到达车流量、周期时长、绿信比和路段长度决定.到达车流量越大，周期越长，绿信比越小，路段越短，截距越大.

由图2（a）可见，当C、u、L一定，不同q形成的L rd－N曲线族为一系列平行直线，直线斜率相同，到达车流量越大，截距越大；无论N取何值，同一N对应的相同Δq均引起相同的Δ，反之亦然；这说明此时对N和q均不敏感.由图2（b）可见，当q、u、L一定，不同C形成的L rd－N曲线族为一系列平行直线，直线斜率相同，周期越长，截距越大；无论N取何值，同一N对应的相同ΔC均引起相同的Δ，反之亦然；这说明此时对N和C均不敏感.由图2（c）可见，当q、C、L一定，不同u形成的L rd－N曲线族为一系列平行直线，直线斜率相同，绿信比越大，截距越小；无论N取何值，同一N对应的相同Δu均引起相同的ΔLrd，反之亦然；这说明此时对N和u均不敏感.由图2（d）可见，当q、C、u一定，不同L形成的L rd－N曲线族为一系列平行直线，直线斜率相同，路段越长，截距越小；无论N取何值，同一N对应的相同ΔL均引起相同的ΔLrd，反之亦然；这说明此时Lrd对N和L均不敏感.

因此，在交通控制系统中，合理限制到达车流量或减少滞留车辆数可以有效缓解交通拥挤.

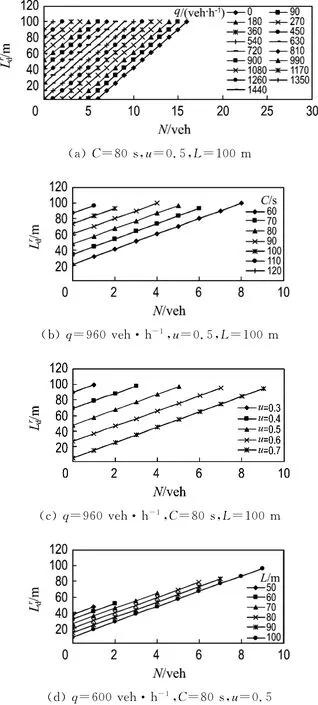
图2 最大当量排队长度与红灯初滞留车辆数Fig.2 Maximum equivalent queue length and number of blocked vehicle at beginning of red light

2.2 时间特性

当N、L、q、u一定，最大当量排队长度与周期时长的函数关系为

从式（10）来看，当N、L、q、u一定，Lrd与C呈线性关系，见图3.直线斜率由到达车流量和绿信比决定，截距由滞留车辆数和路段长度决定.到达车流量越大，绿信比越小，斜率越大.滞留车辆数越多，路段越短，截距越大.

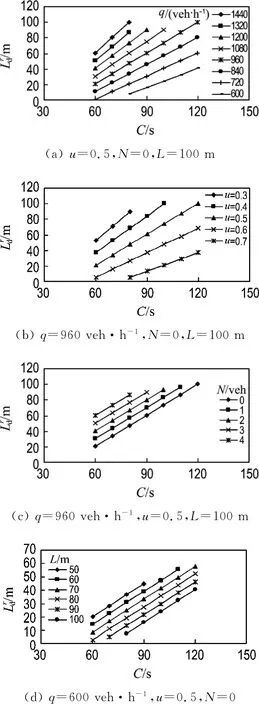
图3 最大当量排队长度与周期时长Fig.3 Maximum equivalent queue length and cycle length

由图3（a）可见，当u、N、L一定，不同q形成的L rd－C曲线族为一系列不平行直线，直线截距相同，到达车流量越大，斜率越大，随着周期变长，直线族由收敛变得发散；周期越长，同一Δq引起的ΔLrd越大，这说明最大当量排队长度对周期较敏感；到达车流量越大，同一ΔC引起的ΔLrd越大，这说明最大当量排队长度在流量低时对周期不敏感，在流量高时敏感，流量越大，越敏感.由图3（b）可见，当q、N、L一定，不同u形成的L rd－C曲线族为一系列不平行直线，直线截距相同，绿信比越大，斜率越小，随着周期变长，直线族由收敛变得发散；周期越长，同一Δu引起的ΔLrd越大，这说明最大当量排队长度对周期较敏感；绿信比越小，同一ΔC引起的ΔLrd越大，这说明最大当量排队长度在绿信比大时对周期不敏感，在绿信比小时敏感，绿信比越小，越敏感.由图3（c）可见，当q、u、L一定，不同N形成的L rd－C曲线族为一系列平行直线，直线斜率相同，滞留车辆数越多，截距越大；无论C取何值，同一C对应的相同ΔN均引起相同的ΔLrd，反之亦然；这说明此时Lrd对C和N均不敏感.由图3（d）可见，当q、u、N一定，不同L形成的Lrd－C曲线族为一系列平行直线，直线斜率相同，路段越短，截距越大；无论C取何值，同一C对应的相同ΔL均引起相同的ΔL rd，反之亦然；这说明此时Lrd对C和L均不敏感.

当N、L、q、C一定，最大当量排队长度与绿信比的函数关系为

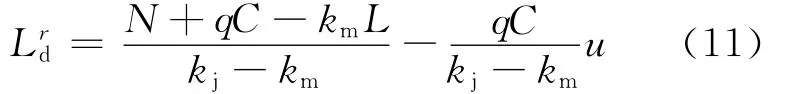
从式（11）来看，当N、L、q、C一定，Lrd与u呈线性关系，见图4.直线斜率由到达车流量和周期时长决定，截距由滞留车辆数、到达车流量、周期时长和路段长度决定.到达车流量越大，周期越长，斜率越小.滞留车辆数越多，到达车流量越大，周期越长，路段越短，截距越大.

由图4（a）可见，当C、N、L一定，不同q形成的Lrd－u曲线族为一系列不平行直线，直线截距相同，到达车流量越大，斜率越小，随着绿信比增加，直线族由发散变得收敛；绿信比越小，同一Δq引起的ΔLrd越大，这说明最大当量排队长度对绿信比较敏感；到达车流量越大，同一Δu引起的ΔLrd越大，这说明最大当量排队长度在流量低时对绿信比不敏感，在流量高时敏感，流量越大，越敏感.由图4（b）可见，当q、N、L一定，不同C形成的L rd－u曲线族为一系列不平行直线，直线截距相同，周期越长，斜率越小，随着绿信比增加，直线族由发散变得收敛；绿信比越小，同一ΔC引起的ΔLrd越大，这说明最大当量排队长度对绿信比较敏感；周期越长，同一Δu引起的ΔL rd越大，这说明最大当量排队长度在周期短时对绿信比不敏感，在周期长时敏感，周期越长，越敏感.由图4（c）可见，当q、C、L一定，不同N形成的L rd－u曲线族为一系列平行直线，直线斜率相同，滞留车辆数越多，截距越大；无论u取何值，同一u对应的相同ΔN均引起相同的ΔLrd，反之亦然；这说明此时Lrd对u和N均不敏感.由图4（d）可见，当q、C、N一定，不同L形成的L rd－u曲线族为一系列平行直线，直线斜率相同，路段越长，截距越小；无论u取何值，同一u对应的相同ΔL均引起相同的ΔLrd，反之亦然；这说明此时Lrd对u和L均不敏感.

因此，在交通控制系统中，适当缩短周期或增加绿信比可以有效缓解交通拥挤.

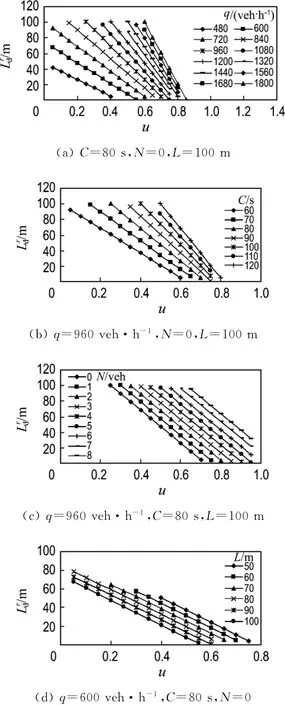
图4 最大当量排队长度与绿信比Fig.4 Maximum equivalent queue length and green ratio

2.3 空间特性

由于最大当量排队长度不能超过路段长度，当路段长度不同时，不同路段上的最大当量排队长度不具有可比性，将最大当量排队长度与其路段长度作比值，称为最大当量排队强度p L，这样就可比较路段长度对最大当量排队长度的影响.

式（7）两端除以L得

在式（12）中令p L＝Lrd/L，当N、q、C、u一定，p L与L呈反函数关系，见图5.根据实际意义，0≤p L≤1.

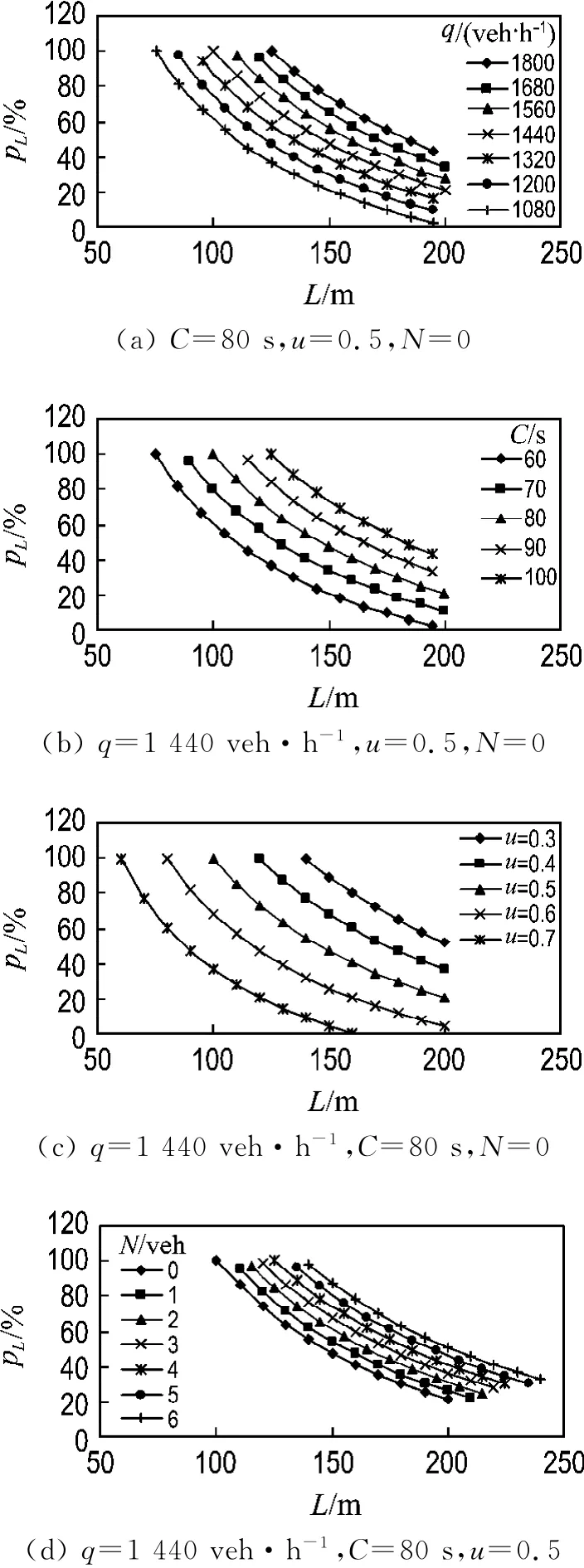
图5 最大当量排队强度与路段长度Fig.5 Maximum equivalent queue percent and length of link

由图5（a）可见，当C、u、N一定，不同q形成的pL－L曲线族为一系列近似平行的反函数曲线，随着路段长度增加，反函数曲线族由窄变宽；路段越长，同一Δq引起的ΔpL越小，这说明ΔpL对路段长度较敏感；路段越短，到达车流量越大，同一ΔL引起的ΔpL越大，这说明排队强度在流量高时对路段长度更敏感，在路段短时对到达车流量更敏感.由图5（b）可见，当q、u、N一定，不同C形成的pL－L曲线族为一系列近似平行的反函数曲线，随着路段长度增加，反函数曲线族由窄变宽；路段越长，同一ΔC引起的ΔpL越小，这说明ΔpL对路段长度较敏感；路段越短，周期越长，同一ΔL引起的ΔpL越大，这说明排队强度在周期长时对路段长度更敏感，在路段短时对周期时长更敏感.由图5（c）可见，当q、C、N一定，不同u形成的pL－L曲线族为一系列近似平行的反函数曲线，随着路段长度增加，反函数曲线族由窄变宽；路段越长，同一Δu引起的ΔpL越小，这说明ΔpL对路段长度较敏感；路段越短，绿信比越小，同一ΔL引起的ΔpL越大，这说明排队强度在绿信比小时对路段长度更敏感，在路段短时对绿信比更敏感.由图5（d）可见，当q、C、u一定，不同N形成的pL－L曲线族为一系列近似平行的反函数曲线，随着路段长度增加，反函数曲线族由窄变宽；路段越长，同一ΔN引起的ΔpL越小，这说明ΔpL对路段长度较敏感；路段越短，滞留车辆数越多，同一ΔL引起的ΔpL越大，这说明排队强度在滞留车辆数多时对路段长度更敏感，在路段短时对滞留车辆数更敏感.

因此，在交通控制系统中，优先协调短路段上、下游交叉口可以有效缓解交通拥挤.

3 灵敏度分析

前面从曲线族的形式上分析了最大当量排队长度对各变量的敏感程度，这些分析比较形象，属于定性分析.下面将运用偏微分方法进一步做定量分析，称为自变量对因变量的灵敏度分析.

从式（7）来看，最大当量排队长度是关于滞留车辆数、到达车流量、周期时长、绿信比和路段长度的一个非线性函数.为分析各变量的灵敏度，对该式求偏导数运算[10].各变量的一阶偏导数为

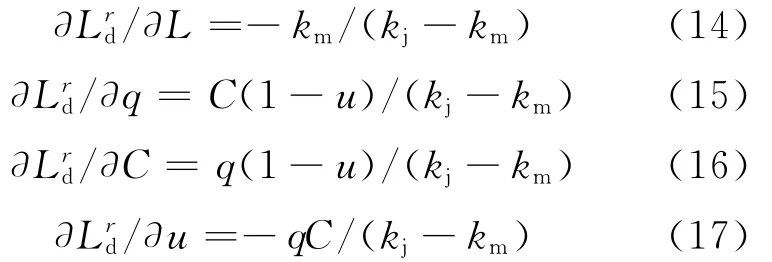
从上式可见，Lrd/N和Lrd/L为常数，Lrd/q、Lrd/C和Lrd/u为变量，这说明最大当量排队长度对滞留车辆数和路段长度的敏感程度与其他变量无关.

比 较 式 （13） 和 （14） 得 ｜Lrd/N｜＜｜Lrd/L｜，这说明最大当量排队长度对路段长度的反应较滞留车辆数更为敏感.

对式（15）～（17）分别求二阶偏导数得

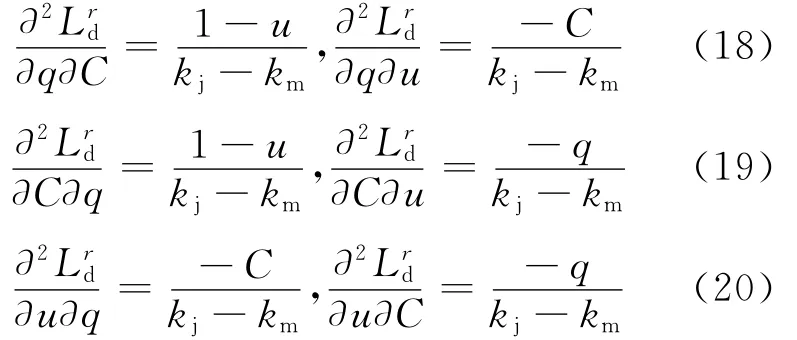
由式（18）～（20）可见，当q、C、u中某个变量一定时，Lrd对另外两个变量的敏感程度相同.

对二阶偏导数求偏导数，得三阶偏导数为

由式（21）～（23）可见，Lrd对q、C、u的敏感程度相同.

对比分析式（13）～（23）可知，最大当量排队长度对路段长度最为敏感，其次为滞留车辆数，对到达车流量、周期时长或绿信比的敏感程度均取决于另外两个变量.

4 结 语

以单车道路段当量排队长度模型为依据，建立了最大当量排队长度模型.通过数理统计方法分析了单个时空参数对最大当量排队长度的影响程度，即其交通流特性、时间特性和空间特性.运用偏微分方法求解了单个时空参数对最大当量排队长度的敏感程度，并分析了这些参数敏感性的优先级.研究成果可为优化或调整交通信号控制方案提供理论依据.

[1]全永燊.城市交通控制[M].北京：人民交通出版社，1989

[2]STEPHANOPOULOS G，MICHALOPOULOS P G.Modeling and analysis of traffic queue dynamics at signalized intersections[J].Transportation Research Part A：General，1979，13（5）：295－307

[3]HEIDEMANN D， WEGMANN H.Queueing at unsignalized intersections [J]. Transportation Research Part B：Methodological， 1997， 31（3）：239－263

[4]CHEVALLIER E，LECLERCQ L.A macroscopic theory for unsignalized intersections [J].Transportation Research Part B：Methodological，2007，41（10）：1139－1150

[5]隽志才，魏丽英，李 江.信号交叉口排队长度宏观模拟的自适应分析法[J].中国公路学报，2000，13（1）：77－80

[6]王殿海，景春光，曲昭伟.交通波理论在交叉口交通流分析中的应用[J].中国公路学报，2002，15（1）：93－96

[7]臧 华，彭国雄.高速道路异常状况下车辆排队长度的预测模型[J].交通与计算机，2003，21（3）：10－12

[8]HERMAN R，PRIGOGINE I.A two－fluid approach to town traffic [J].Science，1979，204（4389）：148－151

[9]姚荣涵，王殿海，曲昭伟.基于二流理论的拥挤交通流当量排队长度模型[J].东南大学学报（自然科学版），2007，37（3）：521－526

[10]丁洁玉，潘振宽，陈立群.基于微分/代数方程的多体系统动力学设计灵敏度分析的伴随变量方法[J].动力学与控制学报，2006，4（3）：205－209