一种新的灰神经网络及其在海洋平台振动控制中应用

崔 洪 宇，赵德有

（大连理工大学 船舶工程学院，辽宁 大连 116024）

0 引 言

灰色系统理论由邓聚龙于1982年首次提出[1]，其广泛用于经济管理、环境科学、控制工程、航空航天等领域[2、3].灰色系统理论通过灰色生成或序列算子的作用来弱化系统的随机性，挖掘系统潜在的规律，计算简单.但是，其预测精度比较低，并行计算能力弱，不太适合预测波动大的复杂系统.神经网络具有很强的抗噪声干扰能力、泛化能力和并行计算能力，但其将系统看做一个黑箱，网络结构很难确定.灰色理论中的灰数是只知道大概范围而不知道其确切值的区间数.神经网络的输出结果是以某一精度逼近一个固定值，由于辨识误差的存在，输出结果在某一中心值附近波动，所以按照灰色理论来定义，神经网络的输出实际上就是一个灰数，神经网络本身就包含灰的内容，因此将灰色理论和神经网络相融合，构造灰色神经网络模型，可以取长补短，充分发挥灰色理论和神经网络各自的优势.目前灰色理论和神经网络主要有以下几种融合方式[4、5]：在同一个系统中用灰色理论和神经网络分别解决不同的问题；灰色理论和神经网络按照串联方式连接；用神经网络来预测灰色预测模型的残差序列；用神经网络对灰色微分方程中的灰色参数进行白化.以往的灰色理论和神经网络的融合都是基于灰色模型G（1，1）和G（1，N）的融合，而基于灰决策理论和神经网络相融合的方法目前还没有看到.灰决策就是从多种对策中选择出最优对策的过程，神经网络也可以看做经过训练来逼近最优对策的过程，所以本文利用灰局势决策理论来构造神经网络的拓扑结构，确定神经网络各层神经元个数及神经元的输入输出运算.但基于原有效果测度的灰神经网络训练过程中很难收敛，所以本文提出一种新的效果测度.最后将本文所构造的基于新效果测度的灰神经网络（GNN）用于控制波浪荷载和风荷载作用下引起的海洋平台的振动响应，并通过数值算例验证本文所提出控制方法的有效性.

1 灰神经网络

1.1 效果测度定义[6]

定义1 设A＝ ｛a1，a2，…，am｝为事件集，B＝ ｛b1，b2，…，bn｝为对策集，S＝ ｛sij＝ （ai，bj）｜ai∈A，bj∈B｝（i＝1，2，…，m；j＝1，2，…，n）为局势集，P＝｛p1，p2，…，pl｝为目标集，u（h）ij≥0（h＝1，2，…，l）为局势sij在目标ph下的效果样本值.

定义2 令Meff为变换，u（h）ij为目标ph下的局势sij（∈S）的效果样本为在Meff下的像，

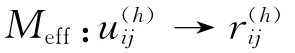
当满足

（1）具有正极性

1.2 新的效果测度及证明

本文提出新的效果测度如下：

定理1 若为正极性，则上限效果测度为

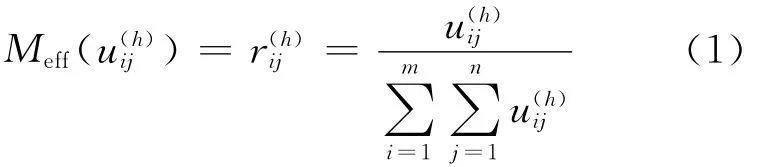
证明 （1）为正极性

（2）∈ [0，1]

定理2 若为负极性，则下限效果测度为

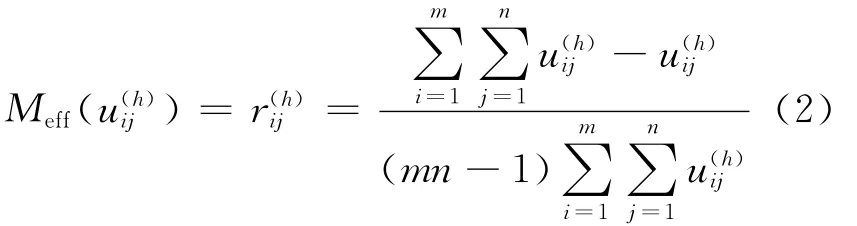
（2）∈ [0，1]

定理3 若为中极性，则适中效果测度为

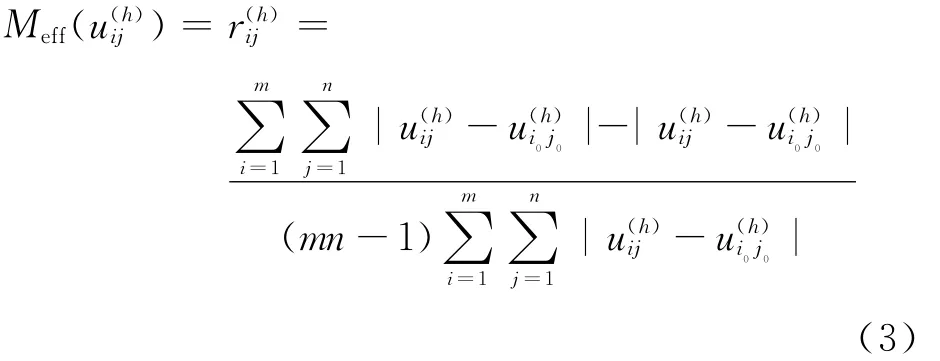
其中为目标ph下的指定效果适中值.证明同定理2证明.

1.3 灰局势决策及算例

灰局势决策是专门解决灰色系统多目标对策问题的一种方法，即对于同一个事件的许多对策，挑选其中效果最好的对策来应对.灰局势决策的具体步骤如下[7]：

步骤1 给定事件集A和对策集B，根据事件集A与对策集B构造局势集S；

步骤2 确定决策目标集P；

步骤3 求局势sij在目标ph下相对应的效果样本矩阵

步骤4 求目标ph下的一致效果测度矩阵，即根据不同的效果测度求效果测度矩阵

步骤5 根据各目标在决策中的权重，确定各目标的决策权η1，η2，…，ηl，其中

步骤7 确定最优局势si0j0.

利用文献[6]中算例（购房的灰局势决策）数据，应用本文的新效果测度灰局势决策方法来计算最优决策.购买住房为事件a1；有3类房屋可供选择（即对策），分别为b1（普通房）、b2（高层住宅）和b3（别墅）；投资者考虑5个目标p1（房价）、p2（质量）、p3（环境）、p4（地理位置）和p5（舒适度）.各类目标下的效果样本和极性如表1所示.

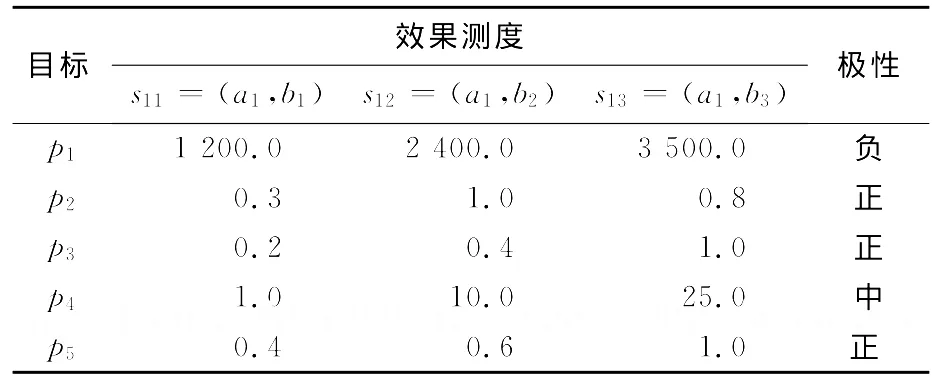
表1 目标下的效果样本和极性Tab.1 Effect samples and polarity in goal

分别应用基于原效果测度和本文新效果测度的灰局势决策计算了综合效果测度，结果见表2.

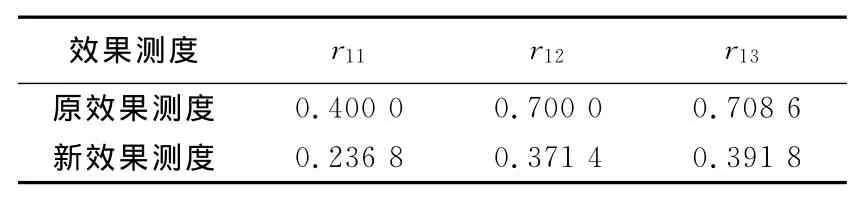
表2 综合效果测度Tab.2 Comprehensive effect measure

本文还应用两种方法分别计算了文献[6]中的算例（深海电缆参数的灰局势决策）、文献[7]中的算例（建设项目方案的灰局势决策），计算得到的综合效果测度结果分别见表3和4.

表3 文献[6]算例综合效果测度Tab.3 Comprehensive effect measure for examplein Lit.[6]

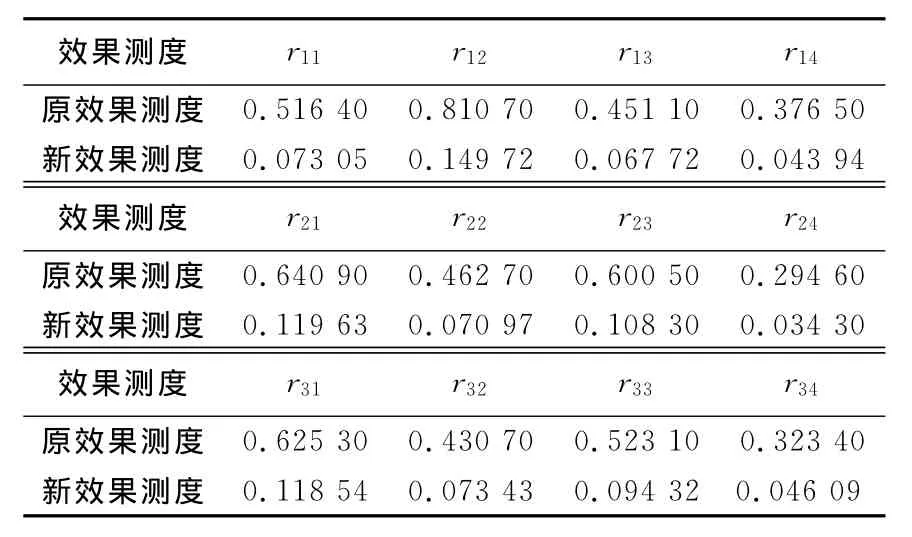
表4 文献[7]算例综合效果测度Tab.4 Comprehensive effect measure for example in Lit.[7]

通过对以上算例结果的分析可以看出，本文提出的新效果测度方法是合理的、有效的.

1.4 GNN结构及训练

本文应用灰局势决策理论来构建神经网络拓扑结构，给定事件集A＝｛a1｝，根据事件集来确定网络的输出为单输出；神经网络结构共5层，网络结构如图1所示.

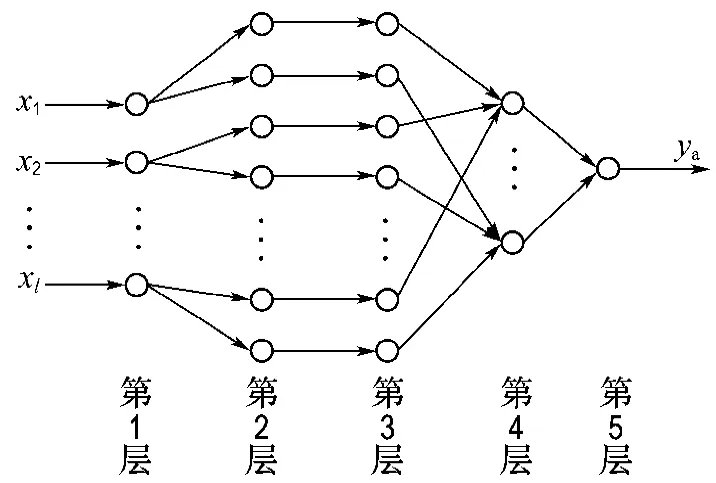
图1 GNN结构Fig.1 Structure of GNN

第1层 输入向量为

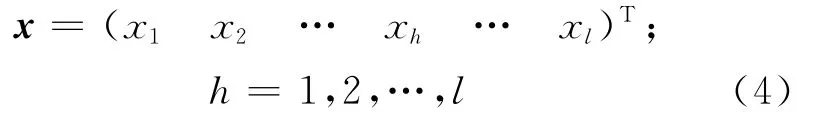
其中，根据目标集P＝ ｛p1，p2，…，p l｝来确定输入空间的维数为l，输入向量的特征x h分别对应灰局势决策目标集中的目标p h.

第2层 该层神经元的激励函数为Gauss函数，神经元的输出为

其中，该层神经元的输出∈[0，1]对应灰局势决策中局势sj（∈S）在目标ph下的效果样本值.chj和σhj分别为各效果样本值对应的中心和方差.

第3层 神经元的输出为

其中，神经元的输出r对应灰局势决策中效果样本值的效果测度

第4层 神经元的输出为

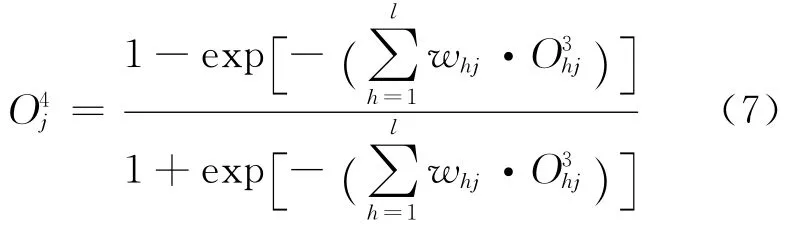
其中w hj为权值.

第5层 输出层，神经元的输出为

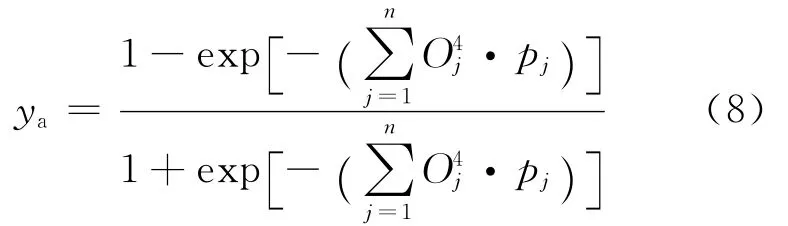
其中p j为权值.

通过梯度下降法训练网络中的各未知参数，取误差指标函数为

其中ds为网络期望输出.

2 基于GNN的海洋平台振动自适应预测逆控制

2.1 导管架式海洋平台模型的建立

导管架式海洋平台属于大柔度复杂结构，平面刚架结构为结构工程中一种较常用的简化计算模型，因此本文将海洋平台简化成平面刚架结构.动态刚度阵法（DSM）可按结构自然节点来划分单元，减少了结构的自由度，简化了计算模型，而且计算结果也十分准确[8].本文采用DSM法建立海洋平台计算机模型.具有n个自由度的受控导管架式海洋平台的运动方程为

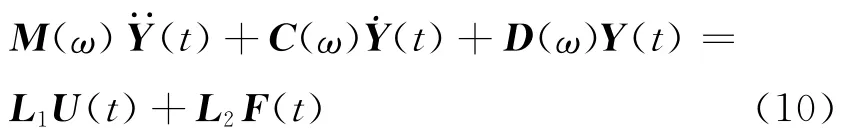
式中：M（ω）和D（ω）分别为n×n阶的总质量和总刚度矩阵，它们都是关于角频率ω的函数；C（ω）为n×n阶总阻尼阵；Y（t）、Y（t）和Y··（t）分别为n维位移、速度和加速度向量；U（t）为m维控制力向量；F（t）为r维外扰力向量；L1为n×m阶控制力位置矩阵；L2为n×r阶外扰力位置矩阵.

2.2 自适应逆控制系统结构

自适应逆控制的过程是首先辨识出被控对象的逆模型，然后将辨识的逆模型串联到被控对象的输入端作为控制器来控制被控对象的动态性能[9、10].本文应用 GNN 辨识平台系统的逆模型作为自适应预测逆控制器，即通过t时刻的平台顶部响应来预测t＋Δt时刻作用在平台顶部的控制力，利用预测控制来减小时滞对控制系统控制性能的影响.用GNN预测逆建模结构如图2所示.

图2 预测逆建模结构框图Fig.2 Block diagram of predictive inverse model

图中，M＝z＋1为导管架式海洋平台系统预测逆建模的参考模型为GNN辨识的平台预测逆模型，P为平台系统模型，us（k）为作用在平台顶部的力，ys（k）为在力us（k）作用下平台顶部的响应为的辨识输出.辨识平台系统的预测逆模型，使误差es（k＋1）→0.由于GNN辨识误差的存在，使得

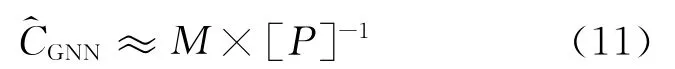
本文基于GNN的自适应预测逆控制系统结构如图3所示.图中z－1为单位延迟，u1（k＋1）和u2（k＋1）为作用在平台顶部的控制力，fa（k＋1）为通过压力传感器采集的作用在平台上的波浪荷载，nb（k＋1）为风荷载等扰动引起平台系统响应的加性噪声.

图3 基于GNN的预测逆控制系统结构框图Fig.3 Block diagram of the control system based on GNN predictive inverse model

自适应预测逆控制系统结构分为两部分：前馈控制部分和扰动消除控制部分.

其中前馈控制部分中存在如下关系式：

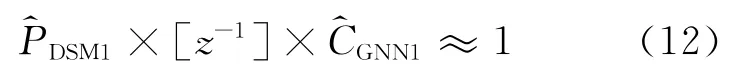
即通过前馈控制器输出预测控制力u1（k＋1）作用在平台顶部，来控制波浪荷载fa（k＋1）作用下引起平台系统顶部的振动响应.

扰动消除控制部分中存在如下关系式：

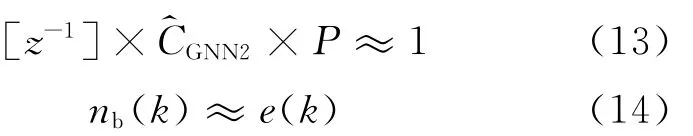
即通过扰动消除控制器输出预测控制力u2（k＋1）作用在平台顶部，来控制风荷载等扰动引起平台系统顶部响应的加性噪声nb（k＋1）.

在系统中将前馈控制、动态刚度阵法建模及GNN辨识中的误差当做被控平台系统响应的加性噪声，用Nb（k）来表示，则

控制系统结构可以等效为图4所示的结构.等效后可以直接采集平台系统顶部的响应信号y，作为的输入信号，这样更有利于进行在线实时控制.

图4 等效的基于GNN的预测逆控制系统结构框图Fig.4 Block diagram of the equivalent control system based on GNN predictive inverse model

3 数值算例

3.1 导管架式海洋平台模型

平台结构总高140 m（距离海床），设计水深80 m，甲板的2层设备层和3层生活区组块高共计20 m，甲板尺寸为60 m×60 m，水平及斜杆尺寸为 0.8 m×0.02 m，竖杆尺寸为 1.6 m×0.04 m，水平支撑4层.桩腿断面尺寸为 1.46 m×0.04 m，桩腿入土深为100 m.导管架式海洋平台桩腿之间的间距比较大，远大于5倍至10倍桩腿直径，故相邻桩腿之间的群桩效应忽略不计.将导管架式海洋平台等效成平面刚架结构，等效后平台由下至上各层的质量分布分别为3000、2500、2000、12000 t，等效后的导管架式海洋平台结构简化示意图如图5所示.

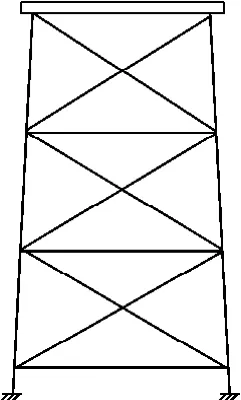
图5 导管架式海洋平台结构简化示意图Fig.5 Sketch of the simplified jacket offshore platform

3.2 GNN设计、训练及泛化

用GNN来辨识导管架式海洋平台的逆模型，GNN的输入为平台顶部的响应（位移、速度、加速度），输出为施加在平台顶部的作用力.根据灰局势决策理论构建神经网络的拓扑结构，选定事件集A＝ ｛a1｝，对策集B＝ ｛b1，b2，…，b7｝，构建局势sij∈S（i＝1；j＝1，2，…，7）.确定目标集P＝ ｛p1，p2，p3｝，其中p1、p2、p3分别对应 GNN的3个输入量，即平台顶部的位移、速度和加速度响应；第2层为21（3×7）个神经元，根据灰局势决策各目标下的效果样本值确定；第3层为21（3×7）个神经元，根据灰局势决策各目标下效果样本值的效果测度确定；第4层为7个神经元，根据灰局势决策中的综合效果测度确定；输出层为1个神经元，根据事件集确定.网络结构中，chj和σhj的初值根据输入数据的范围和离散化的区间来确定，w hj和p j初值选（－1，＋1）均匀分布的随机数.用1500组数据作为训练样本，将输出数据归一化到（－1，＋1）；用1200组数据作为泛化样本，检验本文所提出的GNN的泛化能力，泛化曲线如图6所示.分别用相同的训练样本，对BP网络和基于原效果测度GNN网络进行训练，训练误差见表5.

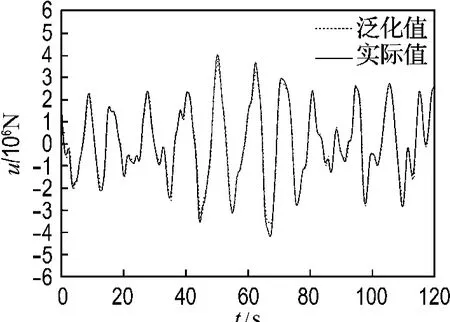
图6 GNN泛化结果Fig.6 Generalized results of GNN

表5 神经网络训练误差Tab.5 Neural network training error

从图6和表5可以看出，基于新效果测度的GNN具有很强的辨识和泛化能力.应用GNN辨识出被控系统精确的逆模型作为控制器，然后连接到被控平台系统的输入端，就形成了预测逆控制系统.

3.3 荷载作用下海洋平台振动主动控制

导管架式海洋平台在复杂的海洋环境中工作，受到的主要荷载为波浪荷载和风荷载，本文通过数值方法模拟波浪荷载和风荷载时程.作用在平台上的波浪荷载采用改进的P－M谱通过Morison公式计算得到[11]，其中波浪的有效波高Hs为7.5 m，平均周期T0为8 s.作用在平台上的脉动风速的时程用线性滤波法中的自回归模型来模拟[12]，其中10 m 高程标准风速为25 m/s，脉动风速的功率谱密度函数采用Davenport谱.图7为数值方法模拟的120 s波浪荷载时程，图8为数值方法模拟的120 s风荷载时程.

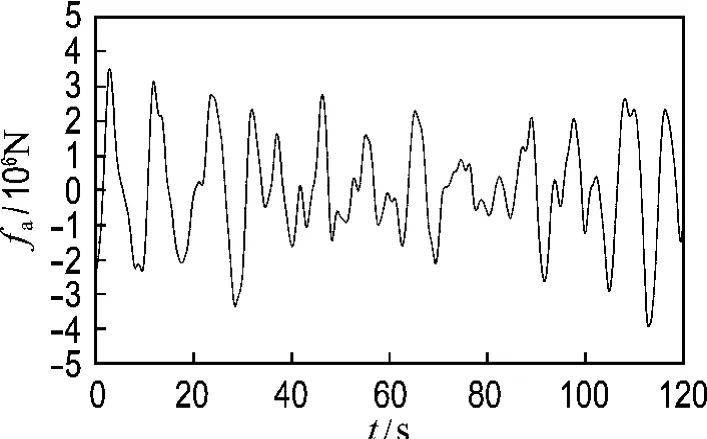
图7 作用在平台上的波浪荷载时程Fig.7 Wave load time history on platform

图8 作用在平台上的风荷载时程Fig.8 Wind load time history on platform

在图7所示的波浪荷载和图8所示的风荷载作用下，平台顶部的位移响应时程如图9所示.从图中可以看出风荷载使平台顶部的位移发生了明显的变化.

应用本文的控制方法，对导管架式海洋平台进行自适应预测逆控制.未控制和控制后平台顶部位移响应时程如图10所示.从图中可以看出，本文的控制方法可有效地控制平台顶部的位移响应.

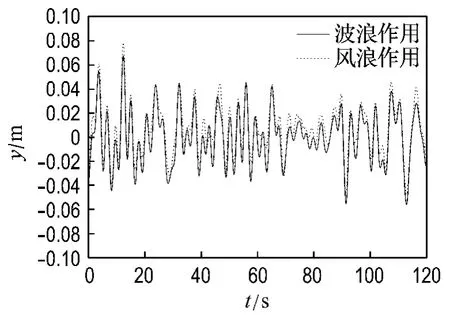
图9 平台顶部位移响应时程Fig.9 Displacement response time history on top platform

图10 未控制和控制后的平台顶部位移响应时程Fig.10 Displacement response time history without and with control on top platform

4 结 语

本文首先提出了一种新的效果测度，并通过证明和算例验证了其合理性和有效性.将基于新效果测度的灰局势决策理论和神经网络相融合，构建了一个新型的灰神经网络，该神经网络结构明确、计算简单，充分发挥了灰局势决策理论和神经网络的优点，弥补了各自的不足.将本文构建的神经网络作为自适应预测逆控制器，对导管架式海洋平台进行振动主动控制.通过数值仿真结果可以看出，本文所提出的灰神经网络具有很强的辨识和泛化能力.基于灰神经网络的自适应预测逆控制方法可以有效地控制在波浪荷载和风荷载共同作用下引起的导管架式海洋平台顶部的位移响应.

[1]邓聚龙.灰色控制系统[J].华中工学院学报，1982，10（3）：9－18

[2]CHIANG H K，CHEN C A，LI M Y.Integral variable structure grey control for magnetic levitation system [J]. Electric Power Applications，2006，153（6）：809－814

[3]LU M，WEVERS K.Application of grey relational analysis for evaluating road traffic safety measures：advanced driver assistance systems against infrastructure redesign [J].Intelligent Transport Systems，2007，1（1）：3－14

[4]万 星，周建中.改进灰色神经网络模型在电量预测中的应用[J].水力发电，2007，33（6）：69－72

[5]XIANG G Y，WEI D Y.The virtual manufacturing model of the worsted yarn based on artificial neural networks and grey theory [J].Applied Mathematics and Computation，2007，185（1）：322－332

[6]邓聚龙.灰预测与灰决策[M].武汉：华中科技大学出版社，2002

[7]刘思峰，党耀国，方致更.灰色系统理论及其应用[M].北京：科学出版社，2004

[8]周 平，赵德有.动态刚度阵法在船体总振动计算中的应用[J].船舶力学，2006，10（4）：126－132

[9]WIDROW Z，WALACH E.Adaptive Inverse Control[M].New Jersey：Prentice－Hall Inc.，1996

[10]SALMAN R.Neural networks of adaptive inverse control systems [J]. Applied Mathematics and Computation，2005，163（2）：931－939

[11]聂 武，刘玉秋.海洋工程结构动力分析[M].哈尔滨：哈尔滨工程大学出版社，2002

[12]舒新玲，周 岱.风速时程AR模型及其快速实现[J].空间结构，2003，9（4）：27－32