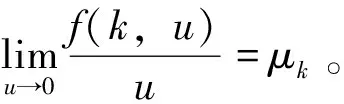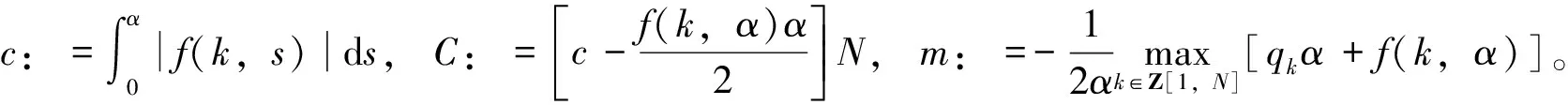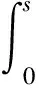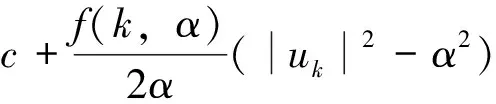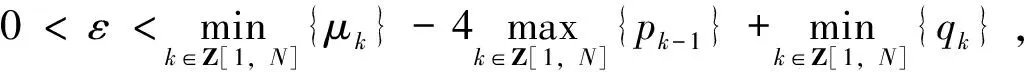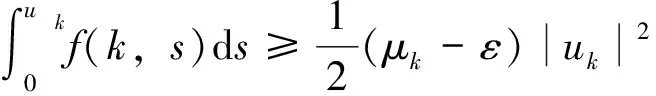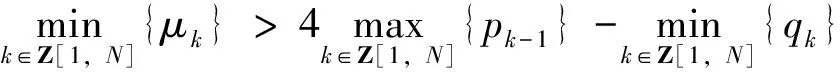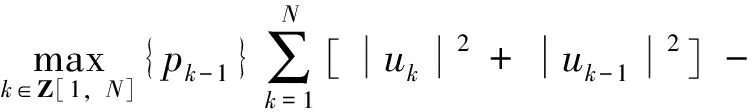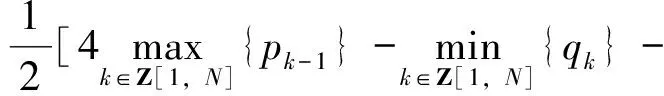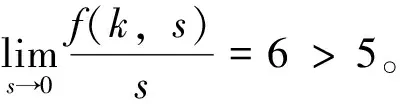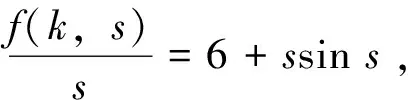一类二阶非线性差分方程边值问题的多重解*

连福云, 徐远通

(1.中国海洋大学数学系, 山东 青岛 266100; 2.中山大学数学与计算科学学院, 广东 广州 510275)

记Z，R分别为整数集与实数集。对于任意的a,b∈Z且a≤b，记Z[a,b]={a,a+1,…,b-1,b}。对于任意给定的正整数N且N>2，我们考虑如下二阶非线性差分方程边值问题 (简记为 BVP)

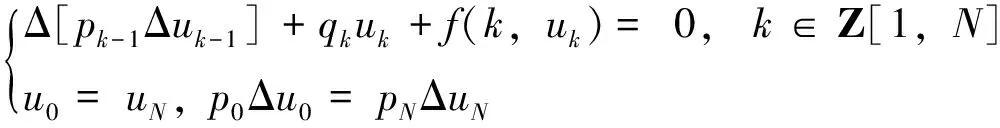
(1)

其中f:Z[1,N]×R→R关于第二个变量连续，pk∈R(k∈Z[0,N])，qk∈R(k∈Z[1,N])， Δuk=uk+1-uk，Δ[pk-1Δuk-1]=pkΔuk-pk-1Δuk-1，k∈Z。方程 (1) 可看作如下方程的离散形式

(p(t)x′(t))′+q(t)x(t)+f(t,x(t))=0,t∈R

该方程是广义的Emden-Fowler方程，关于广义的Emden-Fowler方程的知识可参阅综述文章[1]。非线性差分方程已经广泛应用于研究计算机科学、经济学、神经网络、生态学及控制论等学科中出现的离散模型，关于差分方程的一般背景及基本理论可参阅文献[2-3]。许多作者已经对差分方程边值问题解的存在性应用不同的方法进行了深入的研究，这些方法主要有上下解方法[4-5]、不动点定理[5-6]， 拓扑度理论等[7]。值得注意的是，近几年来已有许多作者用临界点理论研究 BVP 解的存在性，这是很有力的工具，可参阅文献[8-11]。目前关于BVP (1) 多解性的研究结果较少，可见参考文献[10-11]。 文献[10]中作者在满足条件

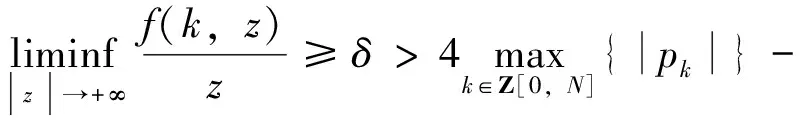
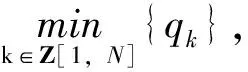
(2)

的前提下得到了BVP (1) 至少有两个非零解的充分条件。文献[11]中作者在满足条件

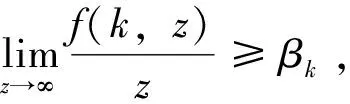
∀k∈Z[1,N]

(3)

的前提下得到了BVP (1) 至少有2N个解的充分条件。

本文利用临界点理论对BVP (1) 的多重解的存在性提出新的判别准则，该结果对条件 (2) 或者 (3) 不满足的情况下仍然可以判断某些BVP (1) 的多重解的存在性。

1 基本引理及变分框架

设E是一个Banach 空间，I∈C1(E,R)。如果u0∈E满足I′(u0)=0，则称u0为I的临界点，I(u0)=c称为I的临界值。如果u(n)⊂E，I′(u(n))有界，I′(u(n))→0 (n→∞) 蕴含u(n)有收敛子列，则称I满足 Palais-Smale条件，简称P.S.条件。令θ表示Banach空间E的零元素，Sn-1表示(n-1)维单位球面。关于临界点理论的基本知识可参阅文献[12-13]。

引理1[13]设E是实Banach空间，I∈C1(E,R)是有下界的偶泛函且满足P.S.条件。假设I(θ)=0，存在集合K⊂E使得K通过奇映射同胚于Sn-1，并且supKI<0。则I至少有n对不同的临界点。

对u=(u1,u2,…,uN)∈RN，令‖u‖max=max{|u1|,|u2|,…,|uN|}，其中|ui|表示ui的绝对值。 对任意k∈Z[1,N]，假设

(H1) 存在α>0使得f(k,α)≤0并且qkα+f(k,α)<0成立；

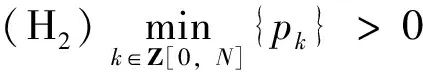
(H3)f(k,u)关于u是奇函数。

定义

引理2 假设(H1)、(H2)、(H3) 对任意k∈Z[1,N]成立，并且存在(u0,u1,u2,…,uN,uN+1)∈RN+2使得

(4)

则‖u‖max≤α，从而(u0,u1,u2,…,uN,uN+1)是 BVP (1) 的解。

证明反证法。假设存在k0∈Z[1,N]使得|uk0|>α及|uk|≤α，k∈Z[1,k0-1]。

(I) 如果uk0>α且k0>1，则u1≤α。由 (H1) 及h的定义知h(k0,uk0)≤0。

一方面，由 (4) 及 (H2)，有pk0Δuk0=pk0-1Δuk0-1-qk0uk0-h(k0,uk0)≥pk0-1Δuk0-1>0。

从而uk0+1>uk0>α并且h(k0+1,uk0+1)≤0。因此

pk0+1Δuk0+1=pk0Δuk0-qk0+1uk0+1-h(k0+1,uk0+1)≥pk0Δuk0>0

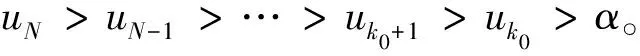
另一方面，根据(4) 的边界条件，有p0u1=p0u0+pNuN+1-pNuN>p0u0=p0uN。从而uN

(II) 如果uk0>α且k0=1，分以下三种情形考虑。

(i) 如果u0α，则由 (H1) 及h的定义知h(1,u1)≤0。由 (4) 及 (H2)，有

当代社会致力于实现可持续性发展与包容性增长，因此，社会治理追求的价值目标不是单一的，面对着人本、公正、效率、秩序、法治等多元价值，必须合理调适价值冲突，努力实现价值平衡。“大调解”体系建设作为一项社会工程，也面临着价值选择与协调的问题。“枫桥经验”导向下的诸暨市的相关探索与实践，为此交出了一份比较理想的答卷。

p1Δu1=p0Δu0-q1u1-h(1,u1)≥p0Δu0>0，从而u2>u1>α且h(2,u2)≤0。因此

p2Δu2=p1Δu1-q2u2-h(2,u2)≥p1Δu1>0，从而u3>u2>α。重复上述过程，得到uN>uN-1>…>u1。

再由 (4) 的边界条件u0=uN知u0>u1，因此得出矛盾。

(ii) 如果u0=u1且u1>α，类似于情形 (i)，有uN+1≥uN≥uN-1≥…≥u1。再由 (4) 的边界条件u0=uN，p0Δu0=pNΔuN，得到uk≡u0，∀k∈Z[0,N+1]。从而由 (4) 及h的定义可得

(iii) 如果u0>u1且u1>α，则由(4) 的边界条件、(H1) 及h的定义知h(N,uN)=h(N,u0)≤0。

一方面，由 (4) 及 (H2)，有

0>p0Δu0=pNΔuN=pN-1ΔuN-1-qNuN-h(N,uN)≥pN-1ΔuN-1

从而uN-1>uN>α且h(N-1,uN-1)≤0。因此

0>pN-1ΔuN-1=pN-2ΔuN-2-qN-1uN-1-h(N-1,uN-1)≥pN-2ΔuN-2

另一方面，根据 (4) 的边界条件，u0=uN，因此得出矛盾。

(III) 如果uk0<-α，由 (H3) 及h的定义，类似于 (I)、(II) 的证明过程可得出矛盾。 证毕。

现在我们建立 BVP (4) 的变分泛函。 令

E={u|u=(u0,u1,…,uN,uN+1)∈RN+2,u0=uN,p0Δu0=pNΔuN}

2 主要结论

若uk>α，则由h的定义，

因此对任意u=(u0,u1,…,uN,uN+1)∈E，

(5)

从而I在E上有下界。

定义

K={(u=(u0,u1,u2,…,uN,uN+1)∈E|‖u‖=ρ}

易知K⊂E且K通过奇映射同胚于SN-1。对k∈Z[1,N]并且u∈K，有|uk|≤‖u‖=ρ

由引理1，I至少有N对不同的临界点。从而 BVP (4) 至少有N对不同的解。再由引理2，BVP (1) 至少有N对不同的解且每个解u=(u0,u1,u2,…,uN,uN+1)∈E满足|uk|≤α，k∈Z[1,N]。

例1 考虑如下边值问题

(6)

参考文献：

[1] WONG J S. On the generalized Emden-Fowler equation [J]. SIAM Rev, 1975, 2 (17): 339-360.

[2] AGRAWAL R P. Difference equations and inequalities [M]. New York: Marcal Dekker, 1992.

[3] ELAYDI S. An introduction to difference equations[M]. 2nd ed. New York: Springer-Verlag, 1999.

[4] AGRAWAL R P, O’REGAN D. Boundary value problems for discrete equations [J]. Appl Math Lett, 1997, 10: 83-89.

[5] HENDERSON J, THOMPSON H B. Existence of multiple solutions for second-order discrete boundary value problems [J]. Comput Math Appl, 2002, 43: 1239-1248.

[6] ATICI F M, CABADA A. Existence and uniqueness results for discrete second-order periodic boundary value problems [J]. Comput Math Appl, 2003, 45: 1417-1427.

[7] THOMPSON H B, TISDELL C. Systems of difference equations associated with boundary value problems for second-order systems of ordinary differential equations [J]. J Math Anal Appl, 2000, 248: 333-347.

[8] AGARWAL R P, PERERA K, O’REGAN D. Multiple positive solutions of singular and nonsingular discrete problems via variational methods [J]. Nonlinear Anal, 2004, 58: 69-73.

[9] BAI D Y, XU Y T. Nontrivial solutions of boundary value problems of second-order difference equations [J]. J Math Anal Appl, 2007, 326: 297-302.

[10] HE X M, WU X. Existence and multiplicity of solutions for nonlinear second order difference boundary value problems [J]. Comput Math Appl, 2009, 57: 1-8.

[11] LIANG H H, WENG P X. Existence and multiple solutions for a second-order difference boundary value problem via critical point theory [J]. J Math Anal Appl, 2007, 326: 511-520.

[12] CHANG K C. Critical point theory and applications [M]. Shanghai: Shanghai Science and Technical Press, 1986.

[13] RABINOWITZ P. Minimax methods in critical point theory with applications to differential equations [C]//CBMS Reg Conf, 65, Amer Math Soc, 1986.