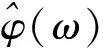一类新三元紧支撑正交小波及其构造*
2010-06-05徐应祥关履泰许伟志
徐应祥,关履泰,许伟志
(中山大学科学计算与计算机应用系, 广东 广州 510275)
小波分析是在Fourier分析基础上发展起来的数学分支,它是Fourier分析、泛函分析、数值分析的完美结晶。自小波分析产生的近二十多年来,小波分析理论逐步得到系统化,其理论包含的内容丰富而深刻,且应用极其广泛,遍及信号分析、图像处理、计算机识别、地震勘探等众多领域。为使小波变换成为真正的实用工具,必须构造不同的小波。对于一元小波的构造经Daubechies等众多学者的工作,其理论与方法已相当成熟[1-7]。但现实世界的大量现象是多元信号,如图像信息和视频信号等。当前,人们大多用张量积(乘积型或可分的)小波处理多元信号。数值实验表明,用张量积小波进行数据的分解与重构不能很好地揭示高频信带的特征。为弥补这些缺陷,就有必要研究非张量积型多元小波的理论和构造方法。注意到设计和构造非张量积正交小波仍然是一件相当困难的工作,现在这方面的工作并不太多[8-13],其理论和方法远不像一元小波那样成熟。
文献[13]提出了一种三元正交小波的构造方法,构造过程相对较为复杂,不易实现,在文献中也没有给出具体的算例。受前人工作的启发,本文的主要目的是给出一类不同于文献[13]的新的三元正交非张量积小波的构造方法。并对相应的结果进行了详细证明,给出具体例子,由构造过程可知该方法较为简单易行。
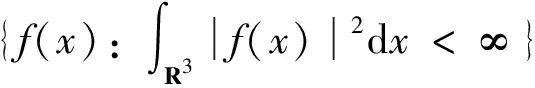
v0=(0,0,0),v1=(1,0,0),v2=(0,1,0),
v3=(0,0,1),v4=(1,1,0),v5=(1,0,1),
v6=(0,1,1),v7=(1,1,1)
则有
(vi+2Z3)∩(vj+2Z3)=φ,i≠j
(1)
其中i,j=0,1,…,7,2T={2x:x∈T},T1+T2={x1+x2:x1∈T1,x2∈T2},φ是空集。换句话说Z3可分解为如下8个子集
{(2i,2j,2k):i,j,k∈Z},
{(2i+1,2j,2k):i,j,k∈Z},
{(2i,2j+1,2k):i,j,k∈Z},
{(2i,2j,2k+1):i,j,k∈Z},
{(2i+1,2j+1,2k):i,j,k∈Z},
{(2i+1,2j,2k+1):i,j,k∈Z},
{(2i,2j+1,2k+1):i,j,k∈Z},
{(2i+1,2j+1,2k+1):i,j,k∈Z}。
定义1 若L2(R3)的闭子空间序列{Vj}j∈Z满足:(i)Vj⊂Vj+1,∀j∈Z
(2)
(3)
(iii)f(x)∈Vj⟺f(2x)∈Vj+1,∀j∈Z
(4)
(iv)f(x)∈Vj⟺f(x-k)∈Vj+1,∀k∈Z3
(5)
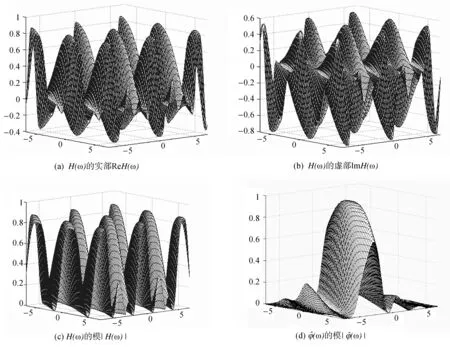
(v)存在函数φ(x)∈V0,使{φ(x-k)}k∈Z3构成V0的一组Riesz基,即存在常数0 (6) 且{φ(x-k)}k∈Z3在V0中完备。 则称{Vj}j∈Z为L2(R3)上的一个多尺度分析,称φ(x)为尺度函数。进一步若{φ(x-k)}k∈Z3构成V0的一组正交基,则称φ(x)为正交尺度函数。以下均设φ(x)为正交尺度函数。 (7) (8) 定理1[12]由式(8)确定的H(ω)满足如下关系: (9) (ii) |H(ω)|≤1,H(0,0,0)=1 (10) (11) (12) 定理2[12]共轭滤波器H(ω)与Gp(ω)(p=1,…,7)有如下关系: (13) (14) 由前可知,构造三维小波正交尺度函数与三维小波函数的关键是构造满足定理1的滤波器H(ω)。由定理1知H(ω)满足如下的条件 H(0,0,0)=1, H(π,0,0)=H(0,π,0)=H(0,0,π)= H(π,π,0)=H(π,0,π)=H(0,π,π)= H(π,π,π)=0 (15) 为满足此条件,我们构造如下形式的H(ω) (16) 其中N1,N2,N3是任意取定的3个正整数,m12,m13,m21,m23,m31,m32是任意取定的6个非负整数。Q(ω)是一个三元三角多项式。显然这样的H(ω)满足条件(15)中除H(0,0,0)=1外的所有条件,但后面可以证明这样构造的滤波器也满足H(0,0,0)=1。 记 再记y1=cos2(u1),y2=cos2(u2),y3=cos2(u3),P(y1,y2,y3)=p1(y1)p2(y2)p3(y3),则P是关于ω1,ω2,ω3的三角多项式,且p1(1-y1),p2(1-y2),p3(1-y3)都是正的仅含余弦的三角多项式,由引理2知存在仅含余弦的三角多项式Q1(u1),Q2(u2),Q3(u3)使得|Q1(u1)|2=p1(1-y1),|Q2(u2)|2=p2(1-y2),|Q3(u3)|2=p3(1-y3)。于是选取Q(ω)=Q1(u1)Q2(u2)Q3(u3),则可得到: 定理3 若取 (17) 其中N1,N2,N3是任意取定的三个正整数,m12,m13,m21,m23,m31,m32是任意取定的六个非负整数,则这样选取的H(ω)满足定理1,即H(ω)是三元正交共轭滤波器。 证明首先,我们有 于是有 而由引理3可知 i=1,2,3 另由构造中所得H(ω)的表达式可知H(π,0,0)=H(0,π,0)=H(0,0,π)=H(π,π,0)=H(π,0,π) =H(0,π,π)=H(π,π,π)=0,因此,在上式中如果令ω=(0,0,0),便立即可得H(0,0,0)=1。 综上所述,如此构造的H(ω)是一个三元正交共轭滤波器。 显然,我们这种方法不同于文献[13]的方法。我们的方法更为简单直接。 定理4 根据定理3中三元正交共轭滤波器H(ω)构造的三元尺度函数φ(x)当m12=m13=m21=m23=m31=m32=0时是可分的,而当m12,m13,m21,m23,m31,m32不全为零时是不可分的。 证明当m12=m13=m21=m23=m31=m32=0时H(ω)是可分的,故如此构造的三元尺度函数是可分的。当m12,m13,m21,m23,m31,m32不全为零时H(ω)是不可分的,故如此构造的三元尺度函数是不可分的。 由定理3,定理4可构造出一大类的三元可分与不可分的正交尺度函数。另外从定理3看出如此构造的三元正交共轭滤波器H(ω)具有有限长度,即只有有限个hk不等于零,因此根据此滤波器构造出的三元尺度函数与小波函数都是紧支撑的。令z1=e-iω1,z2=e-iω2,z3=e-iω3,则定理3构造的共轭滤波器可表为 于是有 定理5 类似于文献[1]中对二元小波理论中的讨论,可选取三元小波对应的Gp(ω)(p=1,…,7)如下 G1(ω)=G1(z1,z2,z3)= (18) G2(ω)=G2(z1,z2,z3)= (19) G3(ω)=G3(z1,z2,z3)= (20) G4(ω)=G4(z1,z2,z3)= (21) G5(ω)=G5(z1,z2,z3)= (22) G6(ω)=G6(z1,z2,z3)= (23) G7(ω)=G7(z1,z2,z3)= (24) 证明由H(ω)的周期性,并应用引理3和引理3中的记号,可知 类似地,经简单计算可知对于其他的m有 因此若令a0j=H(ω+πvj),aij=Gi(ω+πvj),其中i=1,…,7;j=0,1,…,7,则矩阵A=(aij)是一个酉矩阵,所以可如此选取Gp(ω)(p=1,…,7), 并且ψp(x) (p=1,…,7)是相应的三元小波函数。 显然,由于H(ω)具有有限长度,所以由定理5中选取的Gp(ω)(p=1,…,7)也具有有限长度,因此由定理5构造的三元正交小波是具有紧支撑的三元小波。 定理6 用定理3中三元正交共轭滤波器H(ω)构造的三元尺度函数φ(x)具有如下的消失矩性质: (i)当m12=m13=0时,尺度函数φ(x)关于x1具有N1阶消失矩,即 (25) (ii)当m21=m23=0时,尺度函数φ(x)关于x2具有N2阶消失矩,即 (26) (iii)当m31=m32=0时,尺度函数φ(x)关于x3具有N3阶消失矩,即 (27) 例1 取N1=N2=N3=1,m12=m13=m21=m23=m31=m32=0,则 此即三元Harr小波的共轭滤波器。 例2 取N1=N2=N3=1,m12=m13=1,m21=m23=m31=m32=0,则得不可分正交共轭滤波器 例3 取N1=2,N2=N3=1,m12=1,m13=m21=m23=m31=m32=0,则得不可分正交共轭滤波器 图1 ReH(ω),lmH(ω),|H(ω)|及的图形 参考文献: [1] DAUBECHIES I. Lectures on wavelets [M].Philadelphia: Society for Industrial and Applied Mathematics, 1992. [2] DAUBECHIES I. Orthonormal bases of compactly supported wavelets [J]. Comm Pure and Appl Math, 1988, 41: 909-996. [3] 关履泰.小波方法与应用[M]. 北京:高等教育出版社, 2007. [4] ANDREAS R. The wavelet transform on Sobolev spaces and its approximation properties [J]. Numer Math, 1991,58: 875-894. [5] BOWNIK M. The construction ofr-regular wavelets for arbitrary dilation [J]. J Fourier Anal Appl, 2001,7: 489-506. [6] HAN B. Symmetry property and construction of wavelets with a general dilation matrix [J]. Linear Algebra Appl, 2002, 35:207-225. [7] PETUKHOV A. Construction of symmetric orthogonal bases of wavelets and tight wavelet frames with integer dilation factor [J]. Appl Comput Harmon Anal, 2004, 17: 198-210. [8] KAROUI A. A note on the design of nonseparable orthonormal wavelet bases ofL2(R3)[J]. Applied Mathematics Letters, 2005, 18(3):293 -298. [9] LI Y Z. On the holes of a class of bidimensional nonseparable wavelets [J]. Journal of Approximation Theory, 2003,125(2): 151-168. [10] HE W J, LAI M J. Construction of trivariate compactly supported biorthogonal box spline wavelets [J]. Journal of Approximation Theory, 2003,120:1-19. [11] SKOPINA M. On construction of multivariate wavelets with vanishing moments [J]. Appl Comput Harmon Anal, 2006, 20:375-390. [12] 龙瑞麟.高维小波分析[M].北京:世界图书出版公司, 1995. [13] 黄永东,程正兴.三元正交小波的构造[J].应用数学,2006, 19 (1):176-182.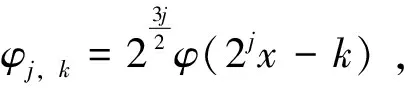

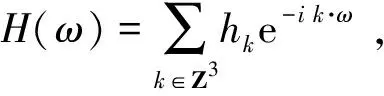

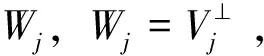
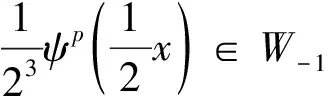
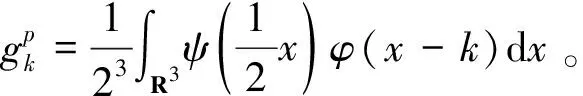
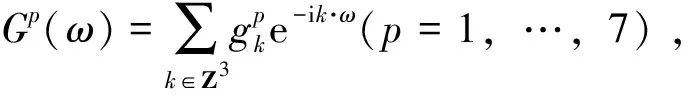
1 三维小波共轭滤波器的构造
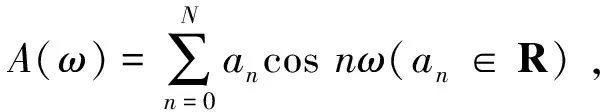
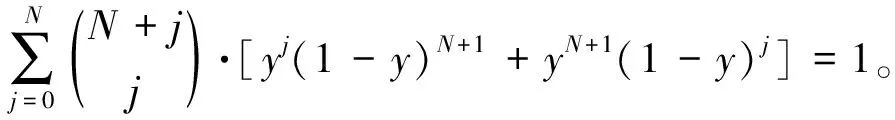

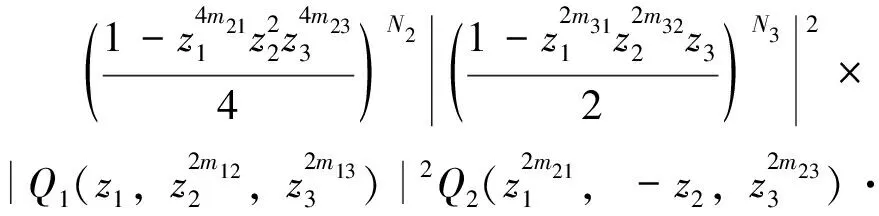

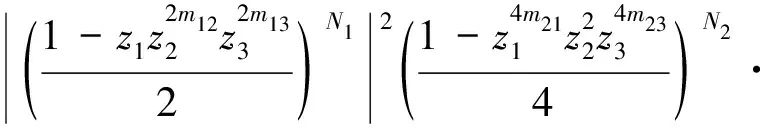
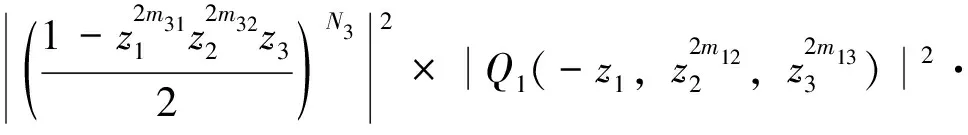
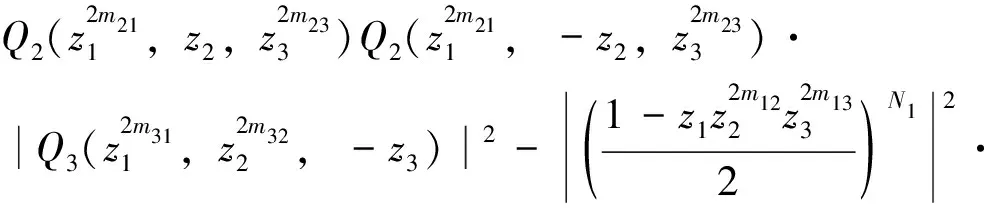
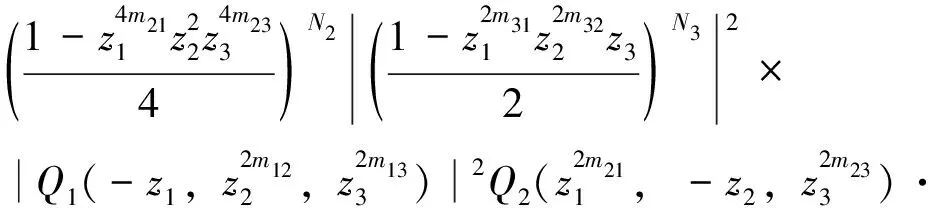
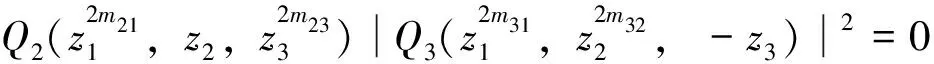
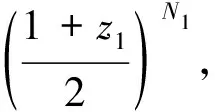

2 数值例子