基于MCE-CA的东莞市紧凑城市形态模拟*
2010-06-05陈逸敏李少英刘小平
陈逸敏,李少英,黎 夏,刘小平
(1.中山大学地理科学与规划学院,广东 广州 510275;2.中山大学管理学院,广东 广州 510275)
我国正处在快速城市化时期,根据中科院的预计,2025年我国城市化水平将达到55%左右[1]。许多城市的发展出现了无序蔓延的状况[2],对资源和环境造成严重的影响[3-4],产生诸如乱占耕地、违背规模经济原理的乡镇工业化等问题[5]。对于城市蔓延的遏制,西方学者提出了紧凑城市(Compact City)、精明增长(Smart Growth)等理论和对策,如Jenks等在其论著中对紧凑城市的概念及其城市形态进行探讨[6-7];国内也有学者根据开展紧凑城市的实证研究[8-10]。在紧凑城市中用地较为密集,对道路交通的依赖大为减少,石油等能源的消耗得以降低[2],因此具有很大的优越性。紧凑型城市的紧凑性体现在诸多方面:如紧凑的空间形态、用地密集布局、集约型的土地利用、人口密度高等特点。研究表明,城市空间形态与可持续发展有密切的联系[11]。本文主要探讨紧凑城市空间形态在抑制城市蔓延方面的积极作用。利用嵌入规划目标的元胞自动机(Cellular Automata,CA)模型,模拟出紧凑的城市空间形态。将规划结果与现实城市形态加以比较,体现紧凑城市形态的优越性。
城市作为一个复杂系统,传统的自上而下的研究方法存在较大的弊端。CA作为一种自下而上的研究方法,常用于自组织系统演变过程的研究[12],很多学者将其应用到城市地理研究中[13-16]。这些研究多集中于城市发展模拟和预测,而城市自身及模拟模型等方面具有诸多不确定性,使CA在城市模拟方面受到一定限制[17]。在CA中嵌入城市规划目标,可以模拟出在各种规划策略下的城市发展情景,因此CA模型在城市规划方面具有很大的价值。目前已有学者开展了将可持续发展理论纳入城市发展规划的CA模拟研究[18-19]。
本文以广东省东莞市为例,利用MCE-CA的方法开展城市形态的模拟。模型考虑了城市发展区位属性和农田适宜性,通过AHP方法确定模型的参数。在模拟2001-2005年的城市形态演变基础上,预测了未加干预情形下2010和2020年的城市空间形态,进而与紧凑城市形态模拟结果进行对比,通过紧凑度和优质农田消耗量来体现紧凑城市形态的优越性。
1 MCE-CA模型
多准则判断CA模型(MCE-CA)最早由Wu和Webster[20]提出,是一种简单、易于实现的CA模型。模型中一个元胞j在t+1时刻的状态由其元胞i及其邻域在t时刻的状态所决定。具体如何发生这种状态的转变,则需要靠转换规则来确定。MCE-CA的转换规则可以用式(1)和(2)表示:
(1)
(2)
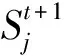
(3)
其中,vn为空间变量,wn为权重。Ri为限制性因素,如当元胞i处于限制发展区时,Ri取值为0;否则取值为1。权重的值可以用层次分析法(AHP)获取[21]。该方法通过将所有变量进行两两比较重要性来最终确定各自的权重。首先建立一个比较矩阵,输入变量两两比较后得到的相对重要性得分,包括:1/9、1/8、1/7、1/6、1/5、1/4、1/3、1/2、1、2、3、4、5、6、7、8或者9。其中1/9表示变量A与变量B相比极不重要,9则表示变量A与变量B相比极重要,1则表示两者同等重要。当输入的得分值能够通过一致性检验时,则产生各个变量的权重值;否则需要重新进行重要性评分以通过一致性检验。
本文将MCE-CA模型用于城市形态模拟,所考虑的区位因素包括一系列空间可达性变量和农田适宜性(varg)。可达性变量包括:市中心可达性(vcity)、镇中心可达性(vtown)、高速公路可达性(vhway)、铁路可达性(vrway)和一般道路可达性(vroad)。由于缺少详细的地块农业适宜度数据,本文使用多年归一化植被指数(NDVI)平均值来近似的替代农业适宜性varg。NDVI指数能够有效反映植物的生长状况,是一种对农田优质程度的间接评价。NDVI利用式4计算,其中TM4、TM3分别为TM影像的4波段和3波段。
(4)
此外,城市发展概率还与局部邻域的发展密度Ω有关。本文将邻域定义为3×3的摩尔邻域,发展密度Ω表示为:
(5)
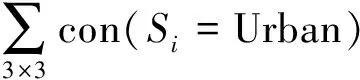
Ra=1+(-lnγ)β
(6)
最后,在考虑发展区位、邻域发展密度和随机性因素后,元胞发展概率可以用式7来表示。在求出元胞i的发展概率之后,利用随机函数生成取值范围为(0, 1)之间的随机数ε,若发展概率大于ε,则i发展为城市用地,否则仍保持当前状态,如式(8)所示。
(7)
(8)
2 研究区及数据
由于缺乏科学规划和管理,东莞市出现了城市发展无序蔓延的问题,大片农田和果园被推平,城市用地呈现较为分散、零乱的格局,直接威胁城市发展的可持续性。通过对1995、1999、2001、2003和2005年的Landsat TM遥感影像进行分类,提取城市用地信息,并计算紧凑度[22]、信息熵[23]的变化情况,如表1所示。各个年份的紧凑度指数都比较低,且不断下降,表明城市用地趋于分散,斑块趋于破碎。信息熵指数逐年上升,同样体现出城市发展日趋无序,空间格局越来越凌乱。因此,有必要通过科学的城市规划,对城市发展进行干预,遏制城市无序蔓延。
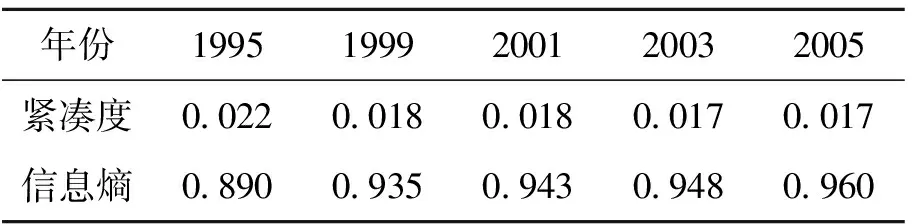
表1 1995-2005年东莞市城市用地紧凑度和信息熵
利用GIS获取模型所需的空间数据,如图1所示,包括2001和2005年的土地利用数据,市中心、镇中心可达性,铁路、高速公路和一般道路可达性,以及农田适宜性。所有数据的分辨率均统一到100 m×100 m;空间变量的数值均进行了归一化,取值范围在0和1之间。

图1 CA模拟所需的空间数据
3 模型运行结果与比较
首先将模型用于现实城市形态演变的模拟。利用专家打分和层次分析法(AHP)求取各个空间变量的权重值,分别为0.082(vcity)、0.124(vtown)、0.274(vhway)、0.074(vrway)、0.404(vroad)和0.042(varg)。将2005年与2001年的土地利用数据叠加,提取新增的城市用地信息。与2001年相比,东莞市2005年新增了160 km2的城市用地,平均每年以5.7%的速度增长,增速很快。城市用地主要沿交通干线扩张,用地呈现出破碎、分散的空间格局。
现实城市形态模拟结果如图2所示,初步的目视判别显示两者的用地空间格局均体现出了较高的一致性。进一步采用点对点比较的方法对模拟结果与实际用地格局进行比较,如表2所示。其中城市用地模拟结果的生产精度、用户精度均超过77%,非城市用地的模拟结果的精度也都超过了80%,整体精度在82%以上,能够满足实际应用的需要。因此,验证结果表明上述权重组合准确反映了各个空间变量在城市发展中所起到的作用,可以用于未来城市空间形态的预测。利用上述权重组合分别模拟了东莞市2010和2020年的城市形态(图2)。为使未来城市形态趋于紧凑,避免用地过于分散、破碎,需要采取措施对城市空间扩张的趋势加以干预。此外,尽管城市发展需要消耗后备的土地资源,如农田,但盲目的城市扩张将会导致大量优质农田的流失。因此,应该有选择性的利用城市后备土地资源,尽量减少优质农田的流失。基于上述规划目标,本文首先利用AHP方法确定各个变量的重要性,加强了农田适宜性,城市中心、镇中心可达性变量的影响,最后得到用于模拟紧凑城市形态的权重值组合:0.297(vcity)、0.245(vtown)、0.065(vhway)、0.047(vrway)、0.048(vroad)和0.298(varg)。
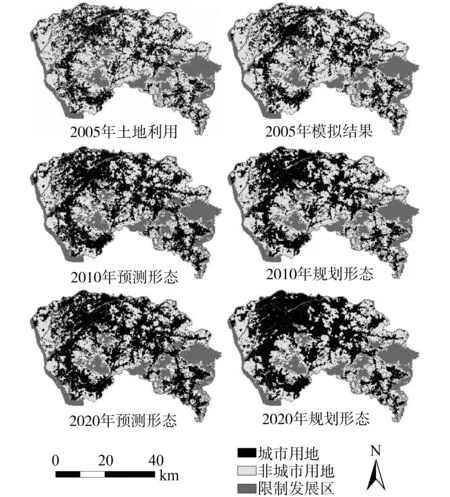
图2 AHP-MCE-CA模拟结果
表2 现实形态模拟结果混淆矩阵
Table 2 Validation of AHP-MCE-CA
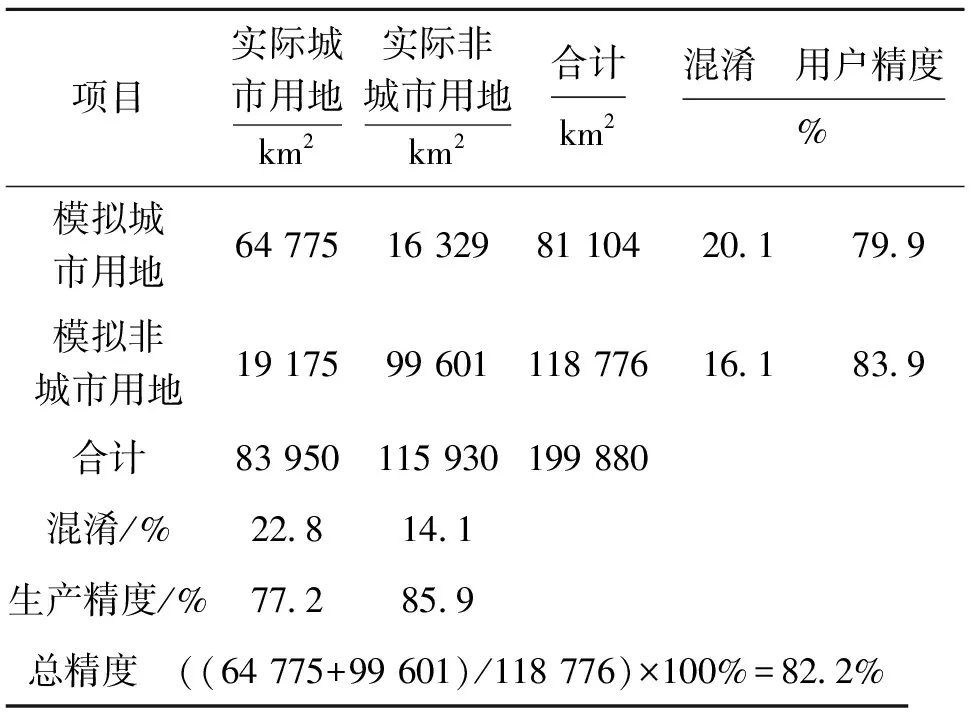
项目实际城市用地km2实际非城市用地km2合计km2混淆 用户精度%模拟城市用地64 77516 32981 10420.179.9模拟非城市用地19 17599 601118 77616.183.9合计83 950115 930199 880混淆/%22.814.1生产精度/%77.285.9总精度 ((64 775+99 601)/118 776)×100%=82.2%
利用紧凑城市形态的权重值组合模拟了2010和2020年的城市形态。初步的目视对比可以发现,在紧凑城市模型的限制下城市无序蔓延的趋势得到了遏制,用地逐渐趋向于紧凑,城市用地凌乱布局的状况得到改善。对紧凑城市形态与预测的现实形态模拟结果进行统计和比较。两者的城市规模在2020年均达到1 166 km2左右,现实城市形态稍高比紧凑形态稍高出1.8 km2。由于对城市空间扩张趋势施加了人为干预,紧凑城市形态在紧凑度上远大于未施加干预的现实城市形态(0.035>0.023,约提高了52.2%)。此外,假定varg> 0.5的属于优质农田,通过统计优质农田损耗情况发现:紧凑城市形态减少了对优质农田的侵占,所消耗的优质农田数量与现实城市形态相比约减少了19.4%(181.1 < 216.3,单位:km2)。可见紧凑城市形态的规划结果能够起到优化城市发展的作用。
4 结 论
当前我国处在快速城市化的阶段,部分城市出现了城市蔓延的情况,若不加以调控势必影响城市的可持续发展。相比之下,紧凑的城市形态因有助于提高用地效率、保证城市发展的可持续性等诸多优点而受到提倡。本文利用在MCE-CA中嵌入规划目标进行紧凑城市形态模拟的方法,生成紧凑型的城市空间格局,并通过与未施加人为干预的现实城市发展形态进行比较。结果表明,紧凑城市形态避免了城市用地凌乱布局的问题,在城市规模与现实发展情形相当的条件下,所消耗的优质农田较少,节省了约19.4%,起到了优化城市发展的作用。
参考文献:
[1] 中国科学院可持续发展战略研究组. 2005年中国可持续发展报告[M]. 北京:科学出版社, 2005: 35-61.
[2] 陈海燕, 贾倍司. 紧凑还是分散?——对中国城市在加速城市化进程中发展方向的思考[J]. 城市规划, 2006, 30(5): 61-69.
[3] MULDAVIN J S S. Environmental degradation in heilongjiang: policy reform and agrarian dynamics in China’s new hybrid economy[J]. Annuals of the American Geographers, 1997, 87(4): 579-613.
[4] ASH R F, EDMONDS R L. China’s land resources, environment and agricultural production[J]. The China Quarterly, 1998, 156: 836-879.
[5] 韩笋生, 秦波. 借鉴“紧凑城市”理念, 实现我国城市的可持续发展[J]. 国外城市规划, 2004, 19(6): 23-27.
[6] JENKS M, BURTON E, WILLIAMS K. The Compact City: A sustainable urban form? [M]. London: E & FN Spon, 1996.
[7] WILLIAMS K, BURTON E, JENKS M. Achieving Sustainable Urban Form[M]. London and New York: Taylor & Francis Group, 2000.
[8] 余颖, 扈万泰. 紧凑城市——重庆都市区空间结构模式研究[J]. 城市发展研究, 2004, 11(4): 59-66.
[9] 付海英, 郝晋珉, 安萍莉,等. 基于精明增长的城市空间发展方向分析——以山东省泰安市为例[J]. 资源科学, 2007, 29(1): 63-69.
[10] 刘纪远, 王新生, 庄大方,等. 凸壳原理用于城市用地空间扩展类型识别[J]. 地理学报, 2003, 58(6): 885-892.
[11] BANISTER D, WATSON S, WOOD C. Sustainable cities: transport, energy and urban form[J]. Environment and Planning B, 1997, 24: 125-143.
[12] WHITE R, ENGELEN G. Cellular automata and fractal urban form: a cellular modelling approach to the evolution of urban land-use pattern[J]. Environment and Planning A, 1993, 25:1175-1199.
[13] CLARKE K C, HOPPENS S, GAYDOS L. A self-modifying cellular automaton model of historical urbanization in the San Francisco Bay area[J]. Environment and Planning B: Planning and Design, 1997, 24: 247-261.
[14] HEROLD M, GOLDSTEIN N C, CLARKE K C. The spatialtemporal form of urban growth: measurement,analysis and modelling[J]. Remote Sensing of Environment, 2003, 86: 286-302.
[15] LI X, YEH A G O. Neural-network-based cellular automata for simulating multiple land use changes using GIS[J]. International Journal of Geographical Information Science, 2002, 16(4): 323-343.
[16] LI X, YEH A G O. Data mining of cellular automata’s transition rules[J]. International Journal of Geographical Information Science, 2004, 18(8): 723-744.
[17] 黎夏, 叶嘉安, 刘涛,等. 元胞自动机在城市模拟中的误差传递与不确定性的特征分析[J]. 地理研究, 2007, 26(3): 443-451.
[18] LI X, YEH A G O. Constrained cellular automata for modelling sustainable urban forms[J]. Acta Geographical Sinica, 1999, 54(4): 289-298.
[19] LI X, YEH A G O. Modelling sustainable urban development by the integration of constrained cellular automata and GIS[J]. International Journal of Geographical Information Science, 2000, 14(2): 131-152.
[20] WU F, WEBSTER C J. Simulation of land development through the integration of cellular automata and multicriteria evaluation[J].Environment and Planning B, 1998, 25: 103-126.
[21] SAATY T L.A scaling method for priorities in hierarchical structures[J].Journal of Mathematical Psychology,1977,15(3):234-281.
[22] 黎夏, 刘凯. GIS与空间分析——原理与方法[M]. 北京:科学出版社, 2006: 88-89.
[23] 黎夏. 珠江三角洲发展走廊1988-1997年土地利用变化特征的时空分析[J]. 自然资源学报, 2004, 19(3): 307-315.
