交流电机铁耗的工程计算方法分析*

罗应立， 赵海森， 姚丙雷， 陈伟华

(1.华北电力大学电气与电子工程学院，北京 102206;2.上海电器科学研究所(集团)有限公司，上海 200063)

0 引言

在中小型电机研制和设计过程中，需要对比分析的设计方案通常可达数十种甚至更多，且对每种方案都要进行必要的损耗分析;在制定电机系统节能方案时，也需要对运行在不同条件下的电机进行损耗分析。损耗分析的难点之一在于铁耗的准确计算，这是由于铁耗影响因素繁多，迄今尚未获得能够反映所有铁耗影响因素的计算公式或模型。因此，简易实用的铁耗工程计算方法便得以广泛应用。

涉及到铁耗计算模型方面的研究，最早可追溯到1892年，Steinmetz首次针对铁磁材料提出了磁滞损耗计算模型［1］;1924年，Jordan进一步将铁磁材料损耗分为磁滞和涡流两项［2］，这一结论在学术界得到普遍认可，在电机铁耗计算中得到广泛应用。通常情况下，铁耗的工程计算方法主要针对齿部和轭部磁路进行计算，且均通过引入经验系数计及铁耗影响因素，不同方法的区别就在于经验系数的选取。以异步电机为例，经典计算方法［3－4］中，计算齿部铁耗时磁滞损耗经验系数取1.2，涡流损耗经验系数取1.5，计算轭部损耗时两者的经验系数均取 2.4;实用计算方法［5，11－13］中，齿部和轭部经验系数分别取2.5和2。此外，相同方法中经验系数也可能不同［11］。

虽然已有大量文献对铁耗工程计算方法进行介绍［3－8，10－13］，但由于其计算方法有多种且每种方法中经验系数各不相同，因此如何选择公式和经验系数成为实际应用中面临的一个首要问题。为此，本文从铁磁材料损耗计算基础出发，对铁耗的几种工程计算方法发展历程及其应用状况进行了系统介绍，并针对目前国内应用最多的实用计算方法，以Y系列不同规格异步电机为例，对其计算误差进行了详细分析;最后对铁耗工程计算方法进行了总体评价，并提出了需要进一步研究的问题及解决途径。

1 交流电机铁耗的计算基础

1.1 交变磁场条件下铁磁材料损耗的分类

在工程中，通常将铁磁材料在交变磁场中产生的损耗分为磁滞和涡流损耗［3－7，10－13］两类。当铁磁材料受周期性磁化时，磁密B和磁场强度H的变化如图1(a)中O→P→Q→R→S→T→O曲线所示，可以看出，当H增加(减小)时，B并不减小(增加)，该过程导致的能量损失称为磁滞损耗;涡流损耗是由于铁磁体的导电性能，当其处于交变磁场时，材料内会感应涡流，进而产生以焦耳热形式消耗的能量［13］，如图1(b)所示。

1.2 实测铁磁材料交变磁化损耗计算模型

1.2.1 磁滞损耗计算模型

对于磁滞损耗，文献［3－4，13］中指出其大小与交变磁化的频率f及磁密B之间有如下关系:

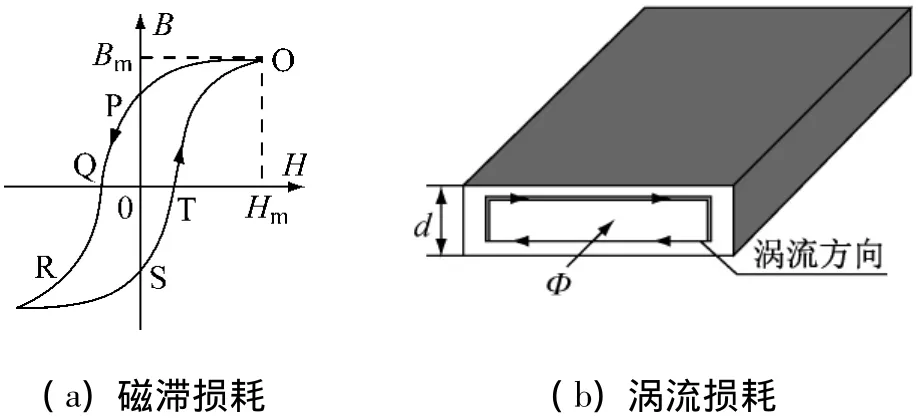
图1 磁滞和涡流损耗

式中:σ——取决于材料特性的常数;

α——磁滞损耗研究的先导Steinmetz命名，称为 Steinmetz系数，通常取 1.6～2.2［3，13］。

两者均可通过损耗测试数据求得。

当磁密小于1 T时，文献［3］中指出式(2)是很精确的:

文献［3－4，13］中还指出，式(3)精度更高:

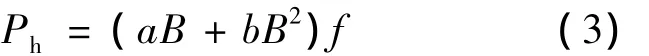
当磁密在1 T≤B≤1.6 T时，式(3)中第一项系数a接近零，而电机内磁密通常都大于1 T，故式中第一项可忽略不计［4，13］，故磁滞损耗仍可按式(1)计算，但与式(1)不同的是式中α取2，如下:

1.2.2 涡流损耗计算模型

对于涡流损耗，文献［3－6，13］在图1(b)所示的硅钢片模型基础上，推导出在正弦交变磁场下，单位重量薄片中的涡流损耗可由式(5)表示:

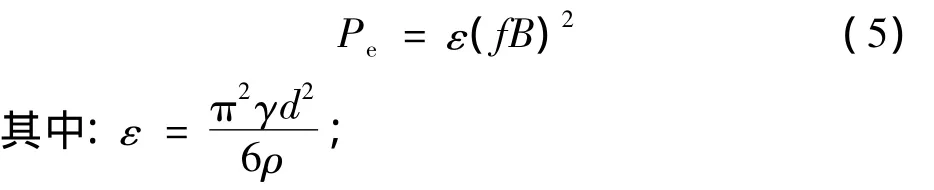
d——硅钢片厚度;

γ，ρ——电导率，质量密度。

1.2.3 考虑到钢片厚度和磁场频率变化时的修正模型

文献［14］指出，随着钢片厚度减小，按照式(5)计算得到的涡流损耗要小于实测值，且钢片越薄，两者差别越大。例如，对于厚度为0.5 mm的钢片，两者差别约为30%;而0.35 mm厚的钢片差别则大于50%，在个别情况下，差别甚至可能达到100%;此外，文献［4－5］也指出类似现象。该情况下，若仍用式(4)、(5)计算磁滞和涡流损耗，势必造成一定误差。为解决这一问题，文献［4］中提出引入损耗影响系数km和kmr，如下。

磁滞损耗的增加可由式(1)乘以系数kmr计及:

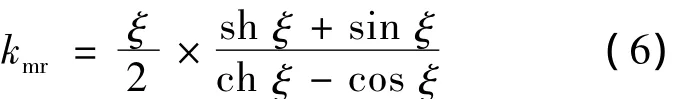
涡流损耗的减小可用式(5)乘以km计及:

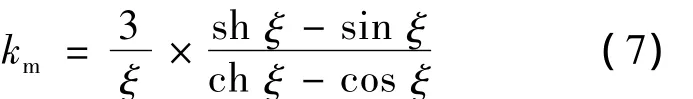
其中:ξ——钢片厚度与其透入深度之比，ξ=d/Δ;

μ，ω——磁导率和角频率。

对厚度为0.5 mm的常用电工钢片，由式(6)、(7)计算得到ξ随f的变化曲线以及系数km和kmr随ξ的变化曲线如图2所示。

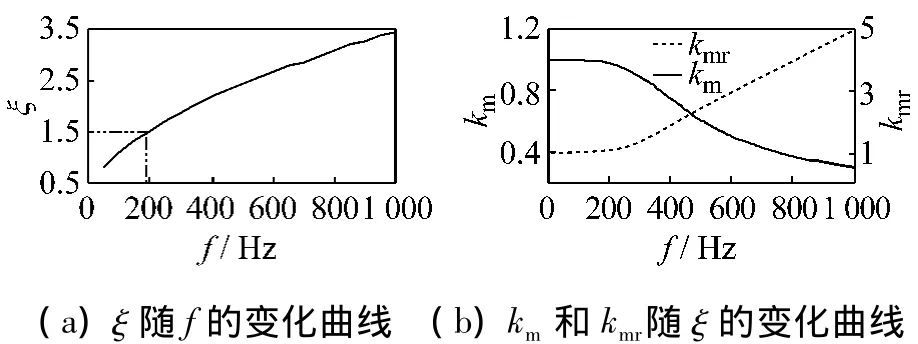
图2 0.5 mm厚电工钢片的磁滞损耗和涡流损耗修正系数

由图中曲线可直观看出，当ξ＜1.5时，系数km实际上接近1;当ξ＜2时，系数kmr接近1。实际上，以常用电工硅钢片为例，其厚度为0.5 mm，电导率为3.3×106S/m，相对磁导率为 3 000，在工频50 Hz情况下，计算可得ξ为0.7，因此在电机正常工作的频率范围内，km和kmr均可取1。对于工作在高频率下或采用高导磁率材料的情况，需要计算其透入深度，根据所得到的ξ值确定是否需要修正。

1.2.4 工程计算方法中电机铁耗的计算模型

综上，对于传统电机，其单位重量损耗计算模型可用磁滞和涡流两项损耗表示如下［3－6，13］:

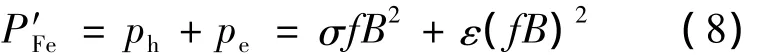
式(8)中损耗系数σ、ε均通过对硅钢片实测损耗数据拟合求得。因此，硅钢片损耗的精确测试便成为铁耗计算的关键。

1.3 常用铁磁材料损耗测试方法

在我国及其他国家的标准中，最常用的硅钢片损耗测试方法是采用所谓“爱普斯坦方圈”(Epstein frame)［15－17］进行测量。其基本结构如图3(a)所示。测试时将裁为窄片的硅钢片，按图3(b)所示端部连接方式叠装，四周套装激磁线圈，钢片交叉处施加一定作用力使其紧密接触。通过测试电压、电流、频率、线圈电阻及输入功率等，就可以进一步得到在交变磁化条件下的硅钢片在不同频率及磁密下的损耗。虽然这种交变磁化状态与电机中旋转磁场的磁化状态并不相同，但是迄今国内、外均以此作为测试及对比硅钢片损耗特性的标准方法。

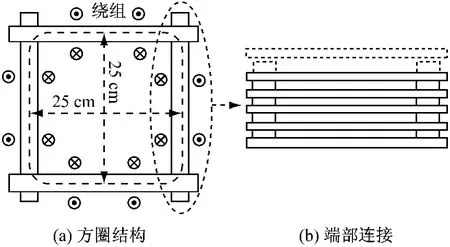
图3 爱普斯坦方圈结构

1.4 交流电机铁耗与交变磁化条件下铁磁材料损耗的区别

对于交流电机，除了交变磁化外，旋转磁化也是产生损耗的主要因素［3－4，13］。文献［3，13］指出，当磁密低于1.5 T时，旋转磁化产生的损耗要高于交变磁化所产生的损耗;文献［18］中针对厚度为0.33 mm的热轧硅钢片，研究了旋转磁化和交变磁化对其损耗的影响，当磁场频率为50 Hz时，两种磁化方式下损耗实测对比结果如图4所示。

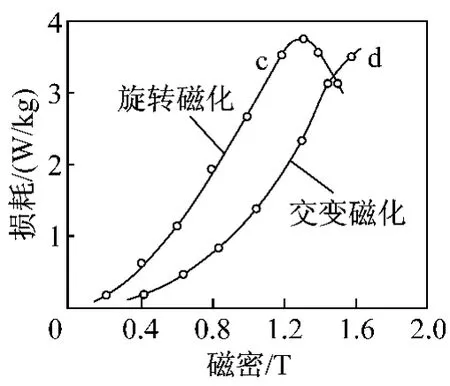
图4 交变和旋转磁化损耗对比［18］

除了磁化方式这一根本区别外，电机铁耗与铁磁材料损耗的其他区别还体现在磁密分布不均匀、制造工艺及谐波磁场等。

2 交流电机铁耗的工程计算方法

由前述可知，式(8)仅为硅钢片在交变磁化条件下的损耗表达式，在利用其计算电机铁耗时，还需要考虑铁耗的众多影响因素。以下对在考虑这些因素后的铁耗计算方法作重点介绍。

2.1 铁耗经典计算方法及其经验系数选择

2.1.1 计及旋转磁化和磁密不均后的铁耗计算

由于旋转磁化主要发生在轭部，因此式(8)仍适用于计算齿部铁耗，但考虑到齿部磁密不均匀分布的因素，式(8)中磁密值采取齿部平均磁密Bav进行计算，故此时铁耗计算表达式为［3］

当考虑旋转磁化和磁密不均匀后，轭部磁滞和涡流损耗计算需引入经验系数Kz和Ky［3］:

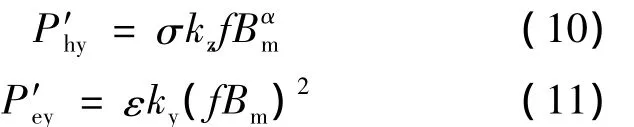
式中，kz≈2，ky=1.2～1.5，式(10)、(11)中的磁密均取轭部最大磁密值Bm。

2.1.2 计及加工影响后的铁耗最终计算公式

文献［3］指出在考虑加工影响后，需引入新的损耗增加系数，结合式(9)～(11)，便可得出齿部和轭部铁耗的最终计算公式。齿部损耗为

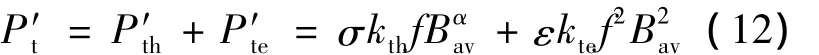
对于同步或异步电机:kth≈1.2、kte≈1.5［4］。

轭部损耗计算公式为［3］

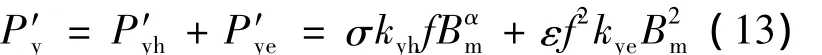
对于所有电机，kyh≈kye≈2.4。需要指出的是式(13)中的系数 kyh、kye已计及式(10)和(11)中的系数 kz和 ky。

2.1.3 附加铁耗计算

对于附加损耗的计算，通常只对空载铁心表面损耗和齿中脉振损耗进行计算，分析如下:

①空载表面损耗。参照文献［3］中的定转子铁心表面损耗的计算公式，将其重新整理如下:

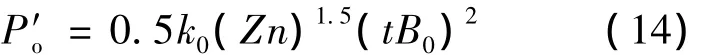
式中:k0——经验系数，对于厚度为0.5 mm电工硅钢片，取其值为2.5;

Z——定子或转子的齿数;

n——转子转速;

t——定子或转子的齿距;

B0——气隙中磁密受开槽影响后的变化幅值，通常取 B0=(KC－1)Bδ;

KC——卡氏系数;

Bδ——气隙磁密幅值。

②空载脉振损耗。参照文献［3］中定转子齿中脉振损耗计算公式，将其重新整理如下:

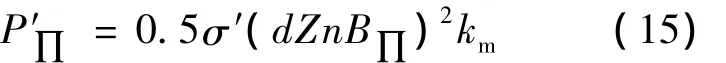
式中:σ′——取决于材料的常数，通常取 σ′=(1.8～2)σ，σ为式(8)中所示的损耗系数;

d——硅钢片厚度;

km——通常取 1;

BП——齿中脉振磁场的幅值。

文献［8］中给出了表面损耗和脉振损耗的解析表达式;文献［9］对表面损耗按照涡流和磁滞两项分开论述，并给出了半经验求解公式，但考虑到传统计算中并不对该项损耗进行详细计算，故文中仅列出式(14)、(15)所述方法，其他计算公式不再一一介绍。

2.1.4 总铁耗计算

电机总铁耗可以利用式(12)～(15)乘以对应的铁心重量即可求得。可以看出上述计算方法是通过引入经验系数来考虑旋转磁化、加工、磁密分布不均匀等铁耗影响因素。

2.1.5 算 例

文献［3］中针对一台1 000 kW、6 000 V、绕组为Y接的绕线式异步电机，按式(10)～(13)对基本铁耗进行计算，得到齿部铁耗为7.6 kW，轭部铁耗为11.7 kW，利用式(15)对定、转子脉振损耗进行计算，分别为0.075 kW和1.975 kW。该算例中忽略了表面损耗。计算中齿部磁滞系数kth为1.2，涡流损耗系数 kte为 1.5;轭部系数 kyh和kye均为 2.4。

2.2 简化的铁耗计算方法及其经验系数选择

虽然利用式(12)～(15)能够计算电机铁耗，但其主要缺点是需要计算的项目多(包括齿部和轭部磁滞损耗、齿部和轭部涡流损耗、附加铁耗)，计算过程较繁琐。因此为了简化计算，进一步将磁滞和涡流损耗以总和的形式进行计算，这种情况下，当钢片厚度为0.5 mm时，在0＜f＜100 Hz的情况下，单位质量损耗就可用式(16)表示［3－4，13］:

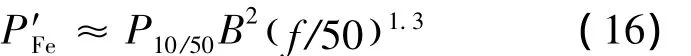
可以看出此时的总损耗与频率的1.3次方成正比，式中P10/50为B=1 T、f=50 Hz时硅钢片的单位重量损耗，其值可以实测，可由硅钢片生产厂家提供，也可根据电机设计手册查表求得。至此，可根据式(13)得出简化后的基本铁耗计算方法:

式中:GFe——钢的总重量;

ka——磁滞和涡流损耗增加系数，其包含了

式(10)～(13)中所提到的铁耗影响因素。

2.2.1 轭部铁耗的简化计算

轭部铁耗按轭部磁路最大磁密Bm计算:

其中:P′Fe≈P10/50B( f /50)1.3，Bm为轭部磁密最大值;文献［4］中指出当电机容量小于100 kW时，ka=1.5;容量大于 100 kW 时，ka=1.3;文献［6］中指出容量小于250 kW时，ka=1.6，容量大于250 kW 时，ka=1.3。

2.2.2 齿部铁耗的简化计算

齿部损耗按齿部磁路平均值Bav进行计算:

其中 P′Fe≈P10/50B( f /50)1.3，文献［4］中指出，对于异步电机 ka=1.8［4］;对于同步电机，当容量小于100 kW时，ka=2.0，容量大于100 kW时，ka=1.7;文献［6］中指出，无论是异步还是同步电机，容量小于250 kW时，ka=1.8，容量大于250 kW时，ka=1.7。

2.2.3 附加铁耗和总铁耗计算

该方法中对于空载附加铁耗的计算仍按照前述式(14)、(15)进行计算。同样，对计算得到的齿部、轭部及附加铁耗进行求和运算即可得总铁耗。

2.2.4 算 例

文献［4］中针对一台14 kW、4极笼型电动机，按照式(19)对定子齿部和轭部的铁耗进行计算，得到轭部铁耗为 0.176 kW，齿部铁耗为0.092 kW，转子齿中的表面损耗为0.037 kW，转子齿中的脉振损耗为0.034 5 kW。该算例中忽略了定子齿中的表面和脉振损耗，轭部和齿部系数分别取 1.3 和 1.8。

2.3 现行实用铁耗计算方法及其经验系数选择

2.3.1 现行实用铁耗计算方法

现行实用铁耗计算方法，是在上述简化计算公式(18)、(19)的基础上，根据工厂实际经验将空载附加铁耗折合为经验系数一起反映到铁耗计算公式中，其表达式为［4－7，10－13］:

式(20)中仅经验系数k和前面所述不同，其包含了旋转磁化、加工、磁密分布不均匀，以及磁通密度随时间不按正弦变化(即谐波磁场产生的附加铁耗)等多种因素，也就是说现行实用计算方法，包含上述考虑的所有铁耗影响因素，其计算结果即为总铁耗。

需要指出的是，利用式(20)计算铁耗时，对于齿部磁路，当定子齿为平行齿时仍取齿部磁密平均值Bav计算，而对于非平行齿，则取靠近齿部最窄1/3处的磁密进行计算［7］;轭部磁路仍选择最大磁密Bm计算，但在计算磁路面积时，圆底槽和平底槽所选择的轭部计算高度有所不同，具体可参考文献［7］和［13］中的处理方法。

2.3.2 经验系数k的选取

为了方便说明，将齿部经验系数定义为kt，轭部经验系数定义为ky。关于经验系数选择，文献［7］和［13］中指出半闭口槽取 kt=2.5、ky=2;对开口槽取 kt=3、ky=2.5;文献［12］中针对大型异步电机，指出当定子为开口槽时，齿部和轭部的经验系数均取3，而定子为半开口槽时，两者均取2.5;此外，文献［11］在对Y系列电机铁耗设计值和试验值进行全面分析的基础上，同时考虑了定子冲片扣片槽对小机座和6、8极电机影响较大的因素，在设计时对上述系数进行了较大修改，根据不同机座号和极对数，kt取值范围为2～3.5，ky取值范围为1.5～3，如表1所示。

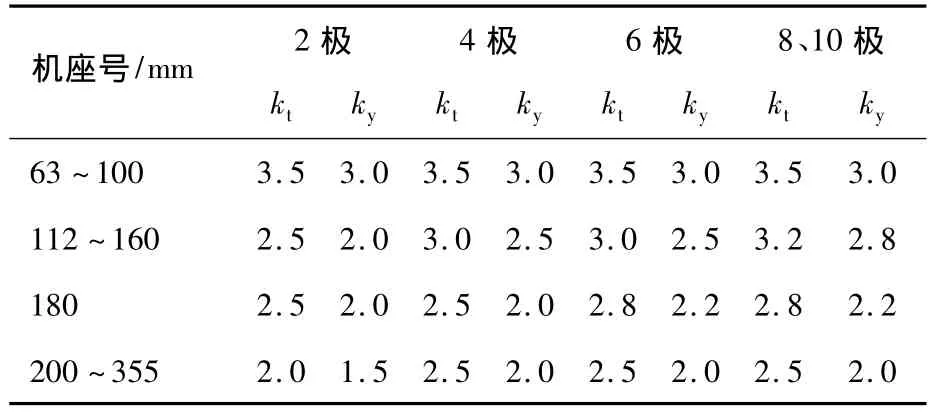
表1 实用铁耗计算经验系数

2.3.3 算 例

①文献［13］中，针对11 kW、4极电机。计算得到轭部铁耗为163 W，齿部铁耗为70.2 W，轭部经验系数为2，在考虑了半闭口槽齿部经验系数取 2.5。

②作者利用该方法对我国Y系列电机典型规格进行了计算，与实测铁耗数据对比如表2所示(注:计算中齿部和轭部经验系数分别取2.5和2)。

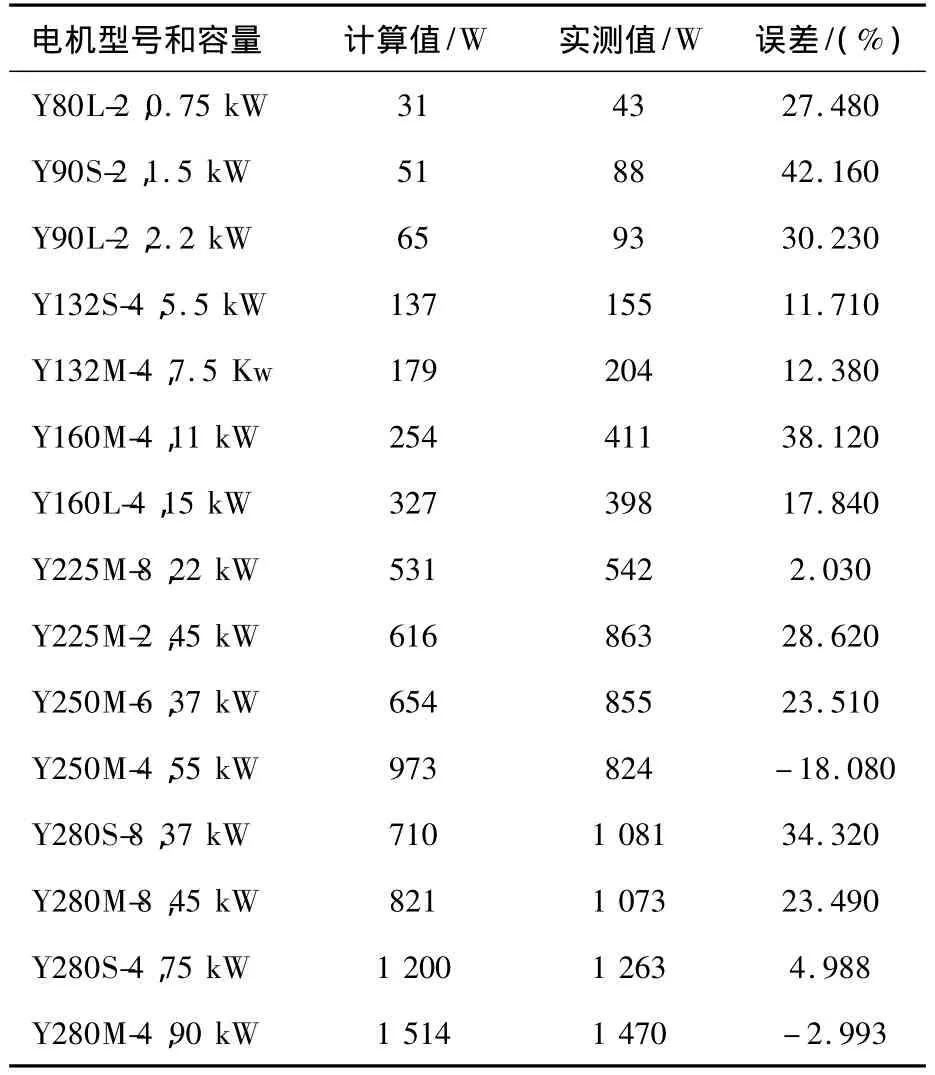
表2 空载铁耗计算和实测值

从表2数据可看出，现行实用计算方法虽然在一定程度上能反映电机的实际铁耗，对于某些电机计算和实测误差在5%范围内，但大多数情况下其计算误差超过10%，最大误差甚至达到42.16%。

2.4 负载附加铁耗的计算

在传统铁耗计算中，通常不对负载附加铁耗进行详细计算，而规定其为输入功率的一定百分数。例如文献［4，12－13］均以输入功率的 0.5%作为其设计值;也有文献针对不同容量电机，推荐了不同的负载附加损耗所占百分数，如文献［19］中对容量在0.75～200 kW之间的电机，所推荐的附加损耗所占百分比在1.5%～3%之间。

3 对铁耗工程计算方法的评价及有待进一步解决的问题

铁耗工程计算方法的优点主要体现在公式简单易用、计算速度快。但由于该方法属于近似计算，在一定程度上不可避免地存在一些不足，分析如下:(1)通过引入经验系数来计及旋转磁化、制造工艺、磁密分布不均匀及谐波磁场等众多影响因素，计算精度较低;(2)依据特定结构、特定制造工艺的实测整机铁耗数据以及工厂实践经验得到的经验系数，难以指导新结构、新工艺电机的研制;(3)计算结果仅反映总铁耗，不便于分析某一特定因素对铁耗的影响，难以指导降耗措施研究。

为了进一步开展新型节能电机的研制工作，需要一种能够计及铁耗主要影响因素且适用于探索电机铁心内部损耗特性的计算方法。基于有限元的铁耗计算方法，能够很好地满足上述要求，其优点在于能够计及电机实际结构、对影响电机铁耗的主要因素(如磁密不均匀、旋转磁化等)不需要引入过多经验系数，同时还能够对电机内部损耗分布进行细致分析，因此开展利用有限元法计算铁耗是很有必要的。已有诸多文献对其进行了研究，但仍有许多问题亟待解决，作者将另有文献对其进行专门介绍。

［1］Steinmetz C P.On the law of hysteresis(originally published in 1892)［C］∥ Proceeding of the IEEE，1984，72(2):197－221.

［2］Jordan H， Die ferromagnetischen konstanten fur schwache wechselfelder［M］.Elektr Nach Techn，1924.

［3］波斯特尼柯夫.电机设计［M］.北京:机械工业出版社，1956.

［4］西安交通大学电机与电器制造教研组.电机设计［M］.北京:中国工业出版社，1961.

［5］第一机械工业部上海电器科学研究所.中小型三相异步电动机电磁计算程序［M］.上海:上海电器科学研究所，1971.

［6］Шуйский В П. Расчет электрических машин［M］.Энергия，1968.

［7］Сергеев Петр Сергеевич，Винограбов Николай Влабимирович， Горяинов Фебор Алексеевич.Проекти－рование Электрических машин ［M ］.ИздЗ－е переработ идоп М Энергия，1969.

［8］上海电器科学研究所中小型电机研究室.三相鼠笼型异步电动机的附加损耗［J］.中小型电机，1975(4):6－14.

［9］秦和.关于小型三相鼠笼型异步电动机附加损耗与转矩曲线的计算［J］.中小型电机，1977(2):6－17.

［10］K Vogt.电机学—旋转电机设计［M］.刘彦清.北京:机械工业出版社，1986.

［11］黄国治，傅丰礼.Y2系列三相异步电动机技术手册［M］.北京:机械工业出版社，2004.

［12］哈尔滨大电机研究所.大型三相异步电动机电磁计算公式［M］.北京:机械工业出版社，1963.

［13］陈世坤.电机设计［M］.北京:机械工业出版社，2008.

［14］Brailsford，Bradshaw.Iron losses at high magnetic flux densities in electrical sheet steel［C］∥ Proceeding of the IEE－Part A:Power Engineering，1955，102(4):463－471.

［15］ASTM A343/A343M－03，Standard test method for alternating－current magnetic properties of materials at power frequencies using wattmeter－ammeter－voltmeter method and 25－cm epstein test frame［S］.2003.

［16］IEC 60404－2，Magnetic materials part 2:methods of measurement of magnetic properties of electrical steel sheet and strip by means of an epstein frame［S］.1996.

［17］GB/T 3655—2008，用爱泼斯坦方圈测量电工钢片(带)磁性能的方法［S］.2008.

［18］C R Boon，J E Thompson.Alternating and rotational power loss at 50 c/s in 3%silicon－iron sheets［C］∥Proceedings of the Institution of Electrical Engineers，1965，112(11):2147－2151.

［19］John Holmquist，P E John Malinowski.Comparison of IEEE 841 1994 to 2001 where might the standard go on the next revision cycle［C］∥ Pulp and Paper Industry Technical Conference，Federal Way，USA，2004(7):1－7.