六相感应电机直接转矩控制系统*

郑 剑， 肖蕙蕙， 李 山

(1.湖南机电职业技术学院，湖南长沙 410151;2.重庆理工大学，重庆 400050)

0 引言

电压源型逆变器驱动的六相感应电机的物理模型如图1所示。逆变器的64种基本开关状态被映射到机电能量转换子空间(dq子空间)和零序子空间(z1z2，o1o2子空间)，即为64个综合电压矢量，如图2所示。传统的六相感应电机直接转矩控制(Direct Torque Control，DTC)系统在每个控制周期内选择dq子空间12个最大矢量中的某一个去控制逆变器和感应电机，从而将定子磁链和转矩控制在相应的滞环带内［1］。该控制策略可以对dq子空间的伏秒进行控制，但不能在一个周期内使z1z2子空间的平均伏秒为零，z1z2子空间的谐波电流可以随意流动。虽然这些谐波电流在双三相绕组中产生的转矩脉动方向相反，在一个周期内相互抵消，但谐波电流相当大，将导致调速系统的体积和成本增加。

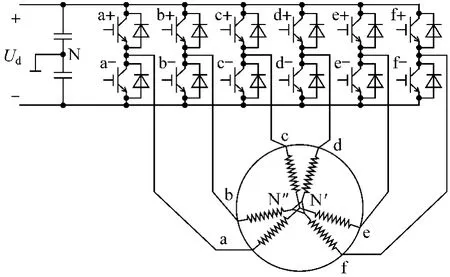
图1 电压型逆变器驱动的六相感应电机

为了解决这一问题，本文对准“定子电流谐波最小”这一控制目标，选择dq子空间12个最大矢量进行合成，得到12个零序平衡矢量。在此基础上，优化设计出一种新型六相 DTC系统，使z1z2，o1o2子空间的定子谐波电流小，从而有效控制定子损耗、减小转矩脉动。最后在Simulink环境下建立该系统的仿真模型，进行仿真试验研究。

1 零序平衡电压空间矢量［2］

由图2可知，dq子空间幅值最大的12个矢量 48、56、60、28、12、14、15、7、3、35、51、49，在 z1z2和o1o2子空间上幅值却最小，因此在z1z2和o1o2子空间会产生最小的谐波电流。选择dq子空间幅值最大的12个矢量进行线性组合，这样可获得高的电压利用率，并可实现转矩和磁链的快速控制;同时可使z1z2，o1o2子空间的谐波电流小，从而有效控制定子损耗，并减小转矩脉动。

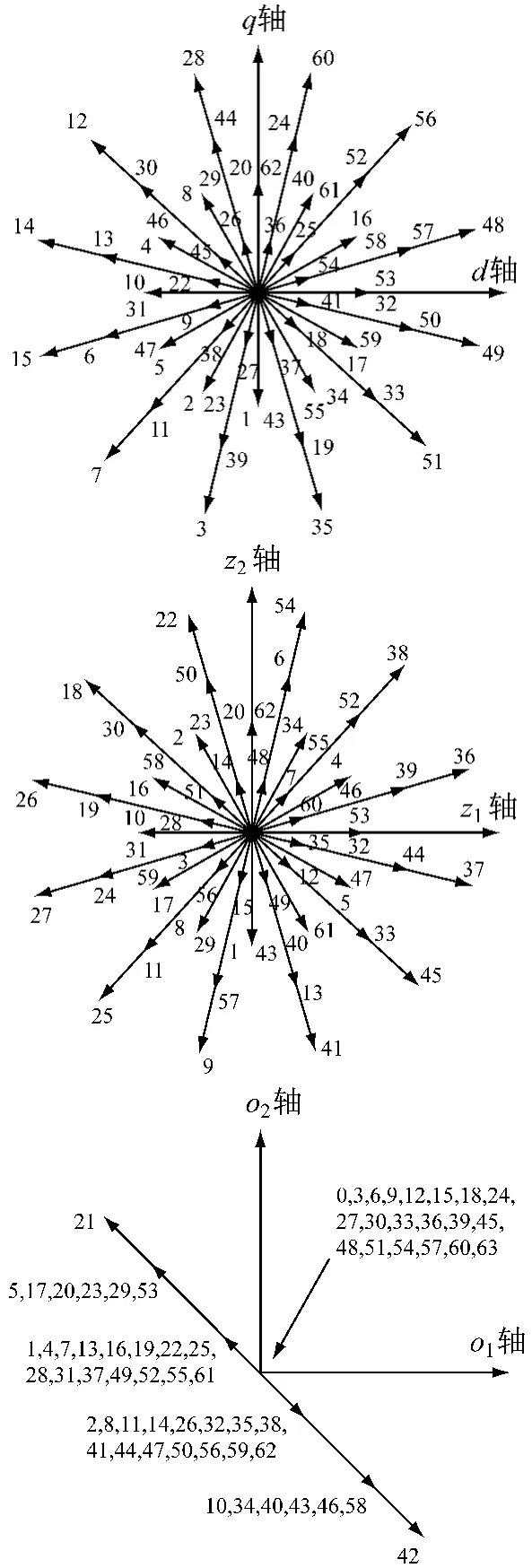
图2 六相逆变器的64种开关状态在三个子空间的映射

选择12个最大矢量中任意三个毗邻矢量，可以合成一个新矢量。若三个毗邻矢量的作用时间符合一特定比例，则可使新矢量在z1z2子空间的平均电压为零。譬如选择毗邻矢量49、48、56，设总的作用时间为Ts，欲使z1z2子空间的平均电压为零，根据伏秒平衡原则，有:

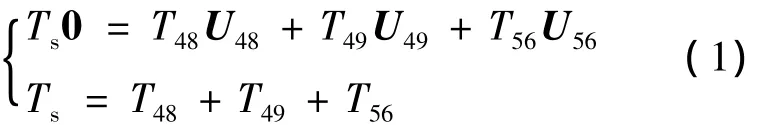
解之得:

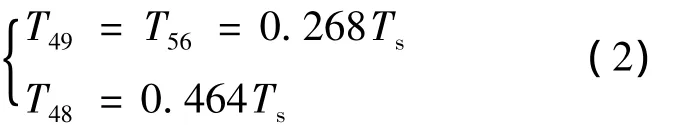
求出毗邻矢量49、48、56的作用时间后，即可求出新矢量在dq子空间的幅值U′和位置。若取调制度为 1，则［3］:

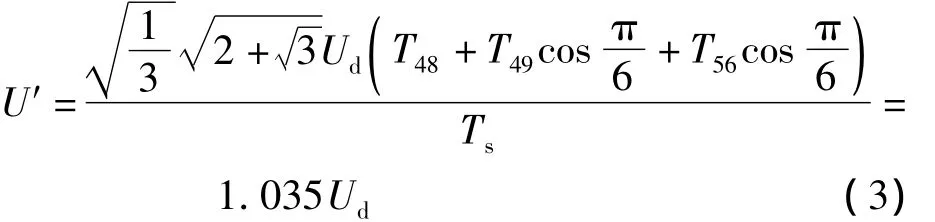
新矢量的位置与矢量48的位置是一致的。

依照此法可得到12个新矢量，分别用 U1′，U2′，…，U12′表示，它们幅值相等，位置互差 π/6，如图3所示。由于新矢量在z1z2子空间的平均伏秒为零，可使定子6k±1次谐波电流得到有效抑制，因此本文将这12个新矢量称为零序平衡矢量。

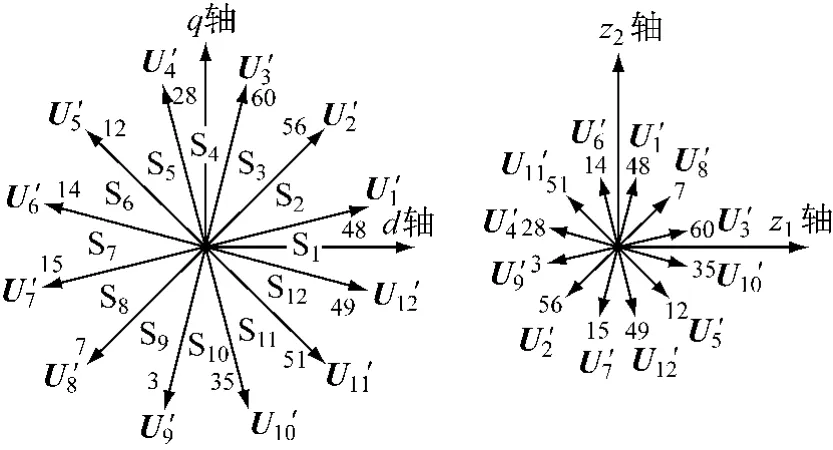
图3 dq子空间的12个最大矢量、12个零序平衡矢量、12个扇区示意图

2 新型六相DTC系统的设计［4］

2.1 总体设计

系统的原理框图如图4所示，逆变器和感应电机被视为一个整体，因此系统主要由磁链和转矩观测器、磁链和转矩调节器、逆变器开关表这三大部分组成，其中磁链和转矩调节器、逆变器开关表构成非线性控制器［5］。

因此，系统设计的三个主要问题是:(1)磁链和转矩观测器的设计;(2)磁链和转矩调节器的设计;(3)逆变器开关表的设计。前两个问题采用常规设计，不赘述;第三个问题采用优化设计。

2.2 逆变器开关表的的优化设计

逆变器开关表的设计包括三张表的设计:(1)零序平衡矢量输出表;(2)综合矢量输出表;(3)开关器件驱动信号输出表。第三张表的设计比较简单，本文关注的是前两者。

利用12个零序平衡矢量将dq子空间划分为12个扇区，如图3所示。当磁链矢量Ψs位于第Ⅰ扇区，且正向旋转(逆时针旋转)时，12个零序平衡矢量对磁链幅值Ψs和转矩Te的影响如表1所示。表中箭头↑↑↑或↓↓↓表示快速增大或快速减小，↑↑或↓↓表示较快增大或较快减小，↑或↓表示增大或减小。

表1 零序平衡矢量对磁链幅值和转矩的影响(当磁链矢量位于第Ⅰ扇区，且正向旋转时)

由于每个电压矢量对转矩和磁链幅值同时产生作用，基速以下，只有磁链幅值恒定，才能获得最快的转矩响应。为此，按照转矩优先磁链的原则选择零序平衡矢量，在磁链幅值和转矩均未达到给定值时，优先控制转矩。因此优化选择的4个零序平衡矢量为 u3′、u5′、u9′、u11′。

当磁链矢量位于其他扇区时，用同样的方法可以优化选择对应的4个零序平衡矢量。再综合QTe、QΨs、sector这三个控制量，得到零序平衡矢量输出表，如表2所示。表中u0x表示4个零综合矢量u0、u21、u42、u63中的某一个，具体选择哪一个，需要再结合上一个控制周期所施加的电压矢量 ，并遵循“最小开关损耗原则”。在Simulink仿真中可以不用考虑开关损耗，因此在仿真中为简单起见，u0x都选择 u0。

表2 零序平衡矢量输出表

表2输出的信息是12个零序平衡矢量和4个零综合矢量中的某一个。每一个零序平衡矢量又对应着3个综合矢量以及这3个综合矢量的作用时间与作用次序。作用时间Tx、Ty、Tz由式(2)确定;作用次序有多种方案，本文采用相同顺序模式。设计的综合矢量输出表，如表3所示，它输出的信息是12个最大综合矢量中的某一个。Tx、Ty、Tz分别表示第一、二、三个综合矢量的作用时间。

表3 综合矢量输出表

3 新型六相DTC系统的仿真［4，6］

建立基于零序平衡矢量的六相DTC系统的Simulink模型。电机参数如下:额定功率5 500 W，额定相电压86 V，额定频率50 Hz，磁极对数 3，转动惯量 0.116 kg·m2，定子电阻0.22 Ω，转子电阻 0.47 Ω，定子电感 0.039 5 H，转子电感0.039 5 H，定转子互感0.036 4 H。其他参数:逆变器直流侧电压Ud=210 V，采样时间Ts=0.000 1 s。

根据上述参数，分别对基于零序平衡矢量的六相DTC系统、基于12最大矢量的六相DTC系统进行对比仿真试验:空载起动，0.3 s施加负载20 N·m，得到的转速、转矩、定子磁链轨迹、a相定子电流、a相定子电流的FFT分析［6］、三个子空间电流的曲线分别如图5、6所示。

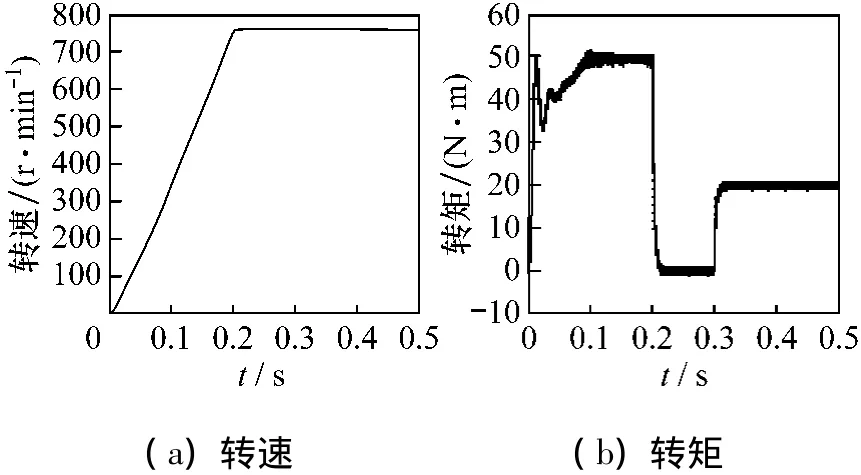
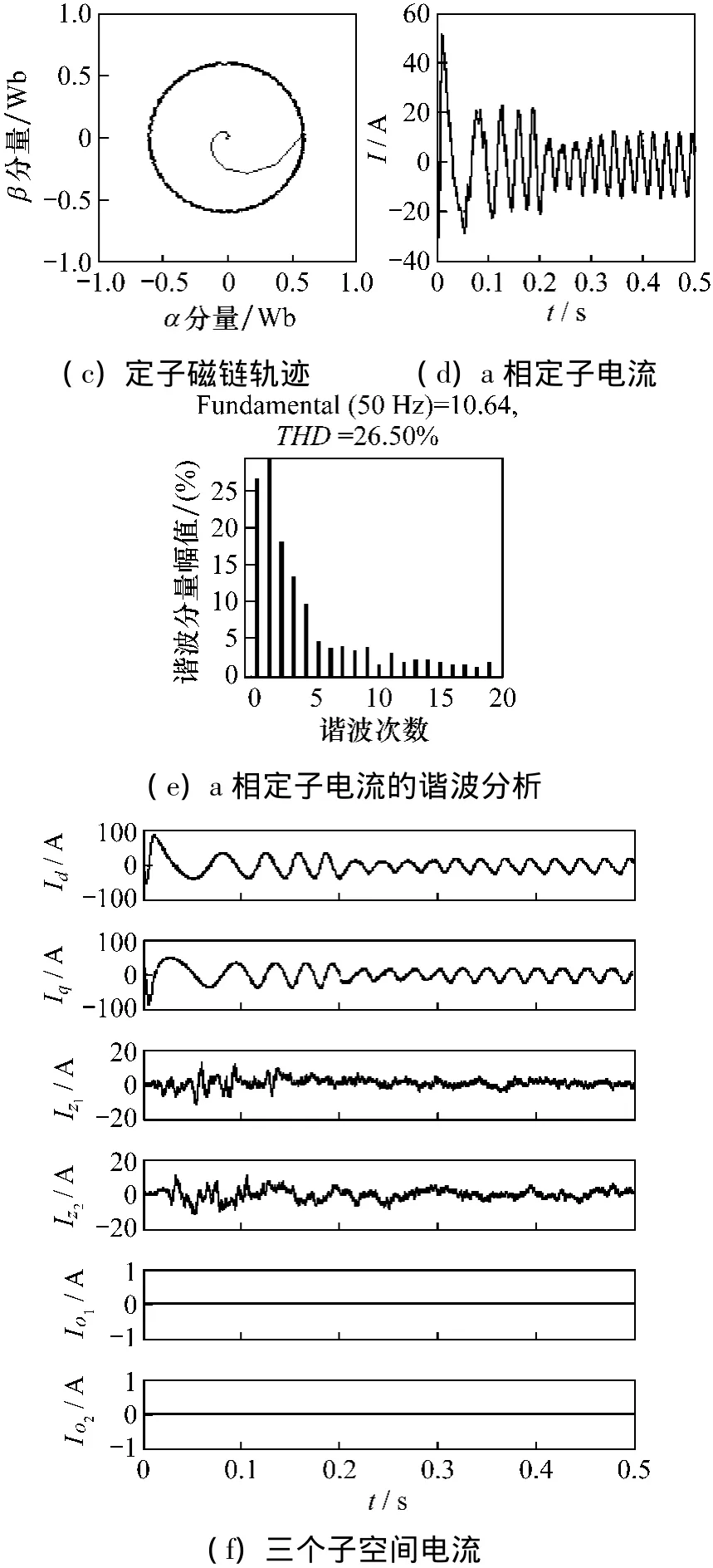
图5 基于零序平衡矢量的六相DTC系统的仿真结果

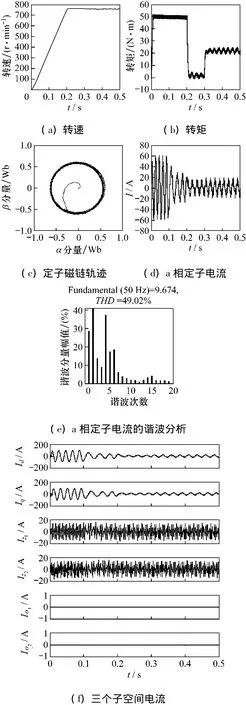
图6 基于12最大矢量的六相DTC系统的仿真结果

对比分析两种系统的仿真曲线可知:两种系统的定子磁链轨迹都为圆形。传统系统的转速曲线0.3 s后有脉动;转矩曲线0.2 s后有周期性脉动，脉动范围为8 N·m;a相定子电流0.3 s后有明显谐波，FFT分析表明THD=49.08%;z1z2子空间电流为－20～20 A，定子谐波电流较大。新型系统的转速曲线无脉动;转矩曲线的脉动较小，脉动范围为2 N·m;a相定子电流0.3 s后没有明显谐波，FFT分析表明THD=26.50%;z1z2子空间的电流为－5～5 A，定子谐波电流较小。因此，设计的系统能够有效减小定子电流谐波和转矩脉动。

4 结语

针对六相感应电机传统DTC系统的定子电流谐波较大、转矩脉动较大的问题，在六相感应电机的动态数学模型、SVPWM算法、基本DTC系统的基础上，设计出一种基于零序平衡矢量的六相DTC系统。在Simulink环境下建立了该系统的各部分仿真模块和总体仿真模型，仿真结果表明，设计的系统能够有效减小定子电流谐波和转矩脉动，从而验证了所提出的控制策略的正确性、有效性。以此为基础，可以对六相感应电机变频调速系统展开更深入的研究。

［1］K Gopakumar，V T Ranganathan，S R Bhat.Splitphase induction motor operation from PWM voltage source inverter［J］.IEEE Transaction on Industry Applications，1993，29(5):927-932.

［2］Li Shan，Xiao Hui Hui.The research of SVPWM control technique of double three-phase induction ［J］.IEEE Trans Energy Conversion，2004，1(3):109-114.

［3］D G Holmes，T A Lipo.电力电子变换器PWM技术原理与实践［M］.周克亮译.北京:人民邮电出版社，2010.

［4］郑剑.六相感应电机直接转矩控制系统的研究［D］.重庆:重庆工学院，2008.

［5］阮毅，陈伯时.电力拖动自动控制系统——运动控制系统［M］.4版.北京:机械工业出版社，2010.

［6］艾永乐，M J Kamper，王玉梅.六相交流感应电机新颖控制策略研究［M］.北京:中国电力出版社，2009.