变频电机铁心损耗计算方法的研究*

刘万太， 彭 晓， 谢卫才， 李永坚

(1.湖南工业大学，湖南株洲 412008;2.湖南工程学院，湖南湘潭 411101)

0 引言

铁心损耗作为电机的主要损耗之一，是电机设计最为关注的问题，尤其是变频电机。因为变频电机的运行频率是可变的，有时高达几百甚至上千赫兹，随着频率的升高，铁心损耗在电机总损耗中的比重也增大;此外，变频电机需要变频器来驱动，而变频器输出中的谐波分量也将在电机铁心中产生附加铁耗。因此，对变频电机铁耗的研究就显得尤为重要。

目前，大部分的铁耗研究都集中在正弦波驱动情况下，并且已经有了比较成熟的理论和试验方法。但是在非正弦波驱动情况下，由于含有大量谐波成分，对变频电机而言，还要进一步考虑铁心材料的饱和特性和集肤效应，铁心材料的铁耗模型发生了变化，传统的铁耗计算方法已不适用于变频器驱动下的异步电机。这就对变频电机铁耗模型提出了更高的要求。本文针对变频电机铁耗研究中铁磁材料特性分析与建模、非正弦激励时电机铁耗计算模型等问题作了系统的综述和分析，并首次提出了谐波铁耗的修正系数，大大提高了变频电机铁耗的计算精度。

1 铁磁材料特性分析及其建模

硅钢片是电机磁路的主要材料，其性能对电机的主要技术指标起着决定性作用。但是在变频器驱动下，随着频率的改变，硅钢片的材料系数也相应的有所改变，这就给变频电机的铁耗分析带来了困难。

为了提高分析精度，在对不同工作状态下的电机进行分析时必须采用相应激励下的硅钢片材料系数。因此，要分析变频电机的铁耗，首先要解决铁磁材料的建模问题。

1.1 铁磁材料的建模

由于频率的改变会对硅钢片的性能产生较大影响，因此变频电机在不同频率下运行时，其硅钢片的铁磁特性也发生了很大变化。硅钢片的铁磁性能测量，特别是在高频下，是相当困难的，且成本很高。通常的做法是利用最佳估计法或神经网络法根据已有的硅钢片材料系数，预测不同频率下的磁化曲线和损耗曲线。

1.1.1 最佳估计法

文献［2］研究了硅钢片在正弦交变磁场下铁心损耗的计算模型如下:

式中:Pfes——单位重量铁心总损耗;

ph——磁滞损耗;

BM——磁密幅值;

f——磁场交变频率;

pe——异常涡流损耗(杂耗中的一部分);

pec——经典涡流损耗(指基波涡流损耗)。

当频率很高时，集肤效应对经典涡流损耗的影响已不能忽略，因此需要在计算公式中加入集肤效应影响因子，如式(2)所示:

式中:a、b、e、x、d 均为材料系数，它们取决于硅钢片材料的物理和化学特性，可利用硅钢片制造商提供的铁耗曲线，通过利用数值分析法中的最佳估计法，对给定的材料特性数据进行曲线拟合，确定材料系数a、b、e、x、d即可完成铁磁材料的建模。

1.1.2 神经网络法

在正弦激励下，一种特定类型的硅钢片材料特性曲线可以用式(3)描述:

式中:H——磁场强度;

Pfes——单位重量硅钢片的铁耗;

B——磁感应强度;

f——激励频率。

由式(3)可知，对于特定类型的硅钢片，其材料特性预测问题可以转换为寻找一个从(f，B)到(H，Pfes)的映射关系。研究表明，可以利用三层前向神经网络来描述硅钢片的材料特性映射问题。利用神经网络的泛化能力来建立硅钢片材料特性预测模型(见图1)。

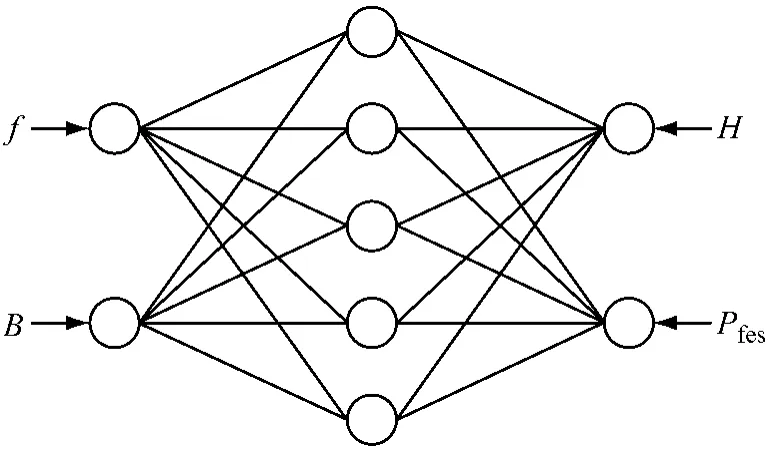
图1 硅钢片材料特性预测的神经网络结构图

将硅钢片制造商提供的产品数据分为两份，选取其中的2/3为学习样本，1/3为测试样本，采用变动量因子和变学习率的改进BP算法对神经网络进行训练，直到网络收敛为止。预测时，只需输入激励频率和工作部位所对应的磁感应强度，便可得到对应磁场强度和单位重量铁耗的预测值。

2 变频电机铁耗谐波分析计算模型

对变频电机而言，采用变频电源供电使电机内磁场波形畸变更加严重。要准确分析铁心中磁通密度的波形，可以通过电磁场有限元的数值分析，比较精确地获得铁心中的磁通密度波形B(t)的数值解。但是该方法实施困难，而且计算量较大，因此通用性较差。本文通过对变频器输出电压特性的分析，采用谐波分析法计算变频电机的铁耗，将非正弦激励时的求解转化为不同频率的正弦信号激励求解问题，再结合任意频率下硅钢片材料特性的预测模型进行分析计算。

变频器的输出中不仅含有基波成分，还含有大量的谐波成分。谐波磁场与基波磁场不同，它不仅在定子铁心中产生损耗而且在转子铁心中也产生损耗。对于变频电机，其谐波铁耗为

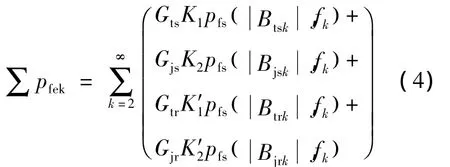
式中:Gtr、Gjr——电机转子齿部、轭部铁心质量;

Btr、Bjr——电机转子齿部、轭部磁通密度幅值;

K′1、K′2——电机转子齿部、轭部铁耗校正系数;

Btrk、Btsk——k 次谐波定、转子齿部磁密;

Bjsk、Bjrk——k次谐波定、转子轭部磁密;

fk——k次谐波频率。

变频电机在非正弦供电时的总铁耗为

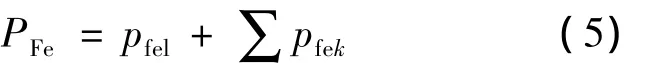
式中:pfel——电源基波所产生的电源基波损耗。

在计算电机铁耗时忽略了局部的磁滞损耗和由于脉动转矩的增加而产生的附加杂散损耗，难免会造成铁耗的计算值较实际值相对较小。此外，谐波损耗的计算往往只考虑对电机铁耗影响较大的部分分量，而忽略了其他高次谐波成分，这也造成了谐波损耗的计算值较实际值较小。在低频运行时，由于转子铜耗的影响较大，实际值与计算值之间的误差会更大。所以依据变频电机的铁耗计算公式求得的铁耗值与电机的实际铁耗值相比较小。针对上述问题，本文提出了谐波铁耗修正系数K′来提高铁耗的计算精度。修正公式为

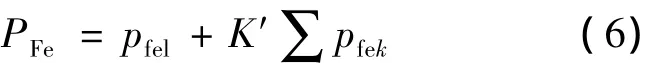
式中:K′为谐波铁耗修正系数，对于不同的运行频率K′的值也不同。当运行频率高于150 Hz时，K′=1.1;当运行频率在50～150 Hz时，K′=1.3;当运行频率在50 Hz以下时，K′=1.4。

由以上分析可知，计算变频电机铁耗的关键在于准确分析铁心中的磁通密度。下面以电机定子齿部磁密为例，作进一步分析。

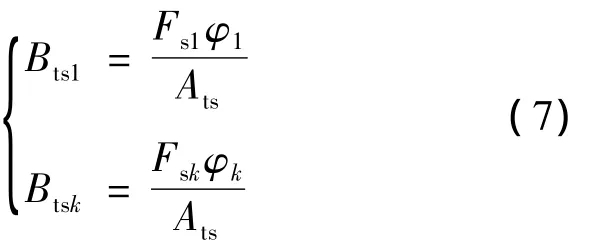
式中:Bts1、Btsk——定子齿部基波和谐波磁密;

φ1、φk——电源基波和谐波所产生的每极主磁通;

Ats——铁心齿部面积;

Fs1、Fsk——基波磁场和谐波磁场下的波幅系数，与铁心磁路的饱和系数相关，考虑到基波磁场和谐波磁场均处于同一磁路，Fs1=Fsk。

每极主磁通φ为

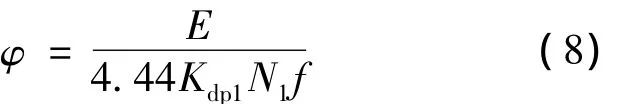
式中:E——定子绕组相电势;

kdp1——绕组系数;

N1——每相串联导体数;

f——磁场交变频率。

下面采用高速变频电机谐波等效电路法进一步分析电机参数，如图2、3所示。

图2 基波等效电路

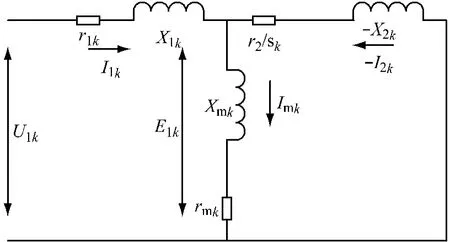
图3 谐波等效电路

图中:r1、r1k——定子侧基波和k次谐波等效电阻;

x1、x1k——定子侧基波和k次谐波漏抗;

r2、r2k——转子侧基波和k次谐波等效电阻(已归算到定子侧);

x2、x2k——转子侧基波和k次谐波等效漏抗(已归算到定子侧);

rm、rmk——基波和 k次谐波激磁等效电阻;

xm、xmk——基波和 k次谐波激磁等效电抗;

s1、sk——基波转差率和k次谐波转差率;

u1和u1k——基波和k次谐波输入电压。

在等效电路参数计算中需要考虑当电机运行频率较高时的集肤效应影响，尤其是对于谐波等效电路，由于谐波转差率近似为1，转子频率skfk远高于基波频率，必须考虑集肤效应对转子导条电阻和漏抗的影响。所以在高频时有以下关系式:r2k=Kr( skfk)r2，x2k=Kx( skfk)x2，Kr，Kx为转子导条的集肤效应系数，对于指定电机，与转子转差频率有关。

因此，在电源的电压特性确定后即可计算出谐波磁场下电机各部分的磁通密度，并由式(2)、(4)、(6)求出变频电机的总铁耗。

3 实例分析与比较

3.1 空载试验

对变频电机进行空载试验，此时电动机的三相输入功率全部克服于定子铜耗、铁耗和转子的机械损耗，其空载损耗如式(9)所示:

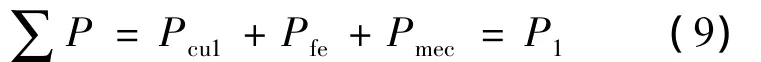
从空载功率P1减去定子铜耗，即得到铁耗和机械损耗之和P′0，如式(10)所示:

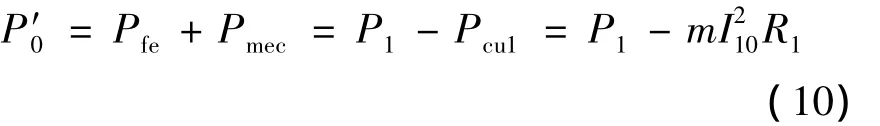
式中:m——电机相数;

I10——电机空载时定子绕组上的电流有效值;

R1——定子每相绕组的电阻。

由于电机的铁耗基本与端电压的平方成正比，机械损耗则仅与转速有关，而与端电压的高低无关，故可以把铁耗和机械损耗两项之和与端电压的平方值画成曲线Pfe+Pmec=f(U21)，则该线近似为一直线，延长其直线部分交与纵轴，从而分离出机械损耗。

试验中以一台1.5 kW基准频率150 Hz的三相异步电动机为样机，铁心材料为冷轧硅钢DW360—50，试验原理如图4所示。

3.2 结果分析

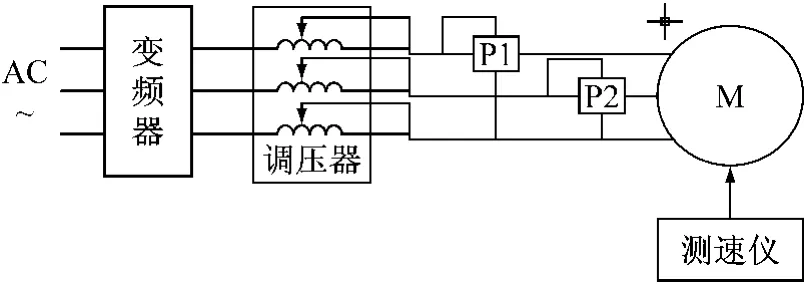
图4 试验测试原理图

将试验测得的铁耗值和谐波分析法及传统正弦经验公式法的计算值进行比较，如表1所示。

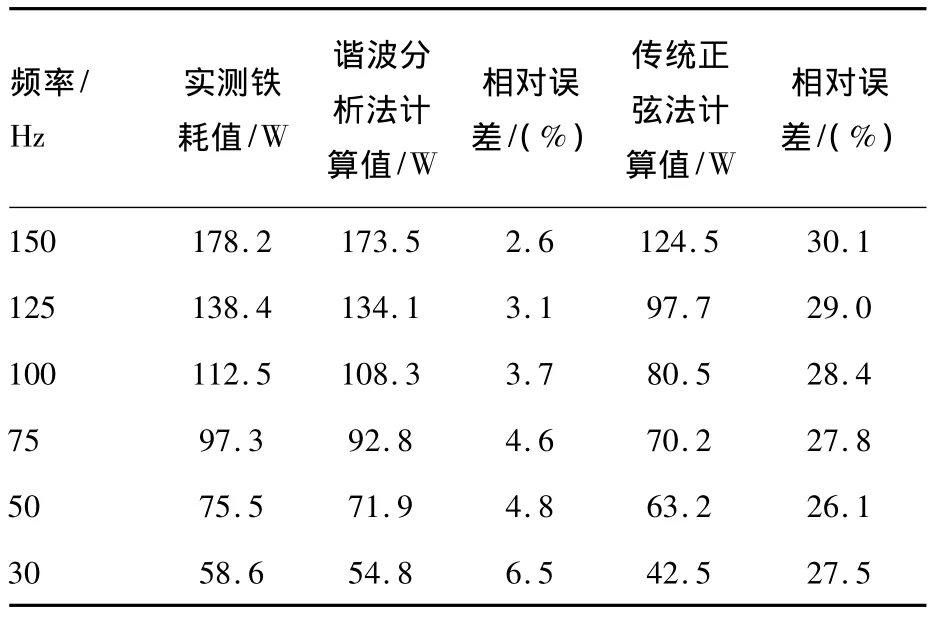
表1 试验测得的铁耗值和计算值的比较

由表1可以看出，试验测得的铁耗值与传统计算方法算得的铁耗值差别较大，而用修正后的谐波分析法计算出来的铁耗值与实测值相差不大，说明本文提出的铁耗计算公式是可行的。

从表1还可以看出，变频电机的运行频率越高，依据谐波分析法计算出的铁耗值与实际值越接近，说明谐波分析法更适用于高速变频电机。

4 结语

本文对正弦交变磁场下硅钢片材料的铁耗计算模型作了系统的分析。在传统谐波分析模型的基础上提出了谐波铁耗修正系数，提高了变频电机铁耗的计算精度。然后对一台样机进行空载试验，试验得到的铁耗值与谐波分析法计算的铁耗值基本一致，而与传统正弦波经验公式的计算值误差较大，说明本文提出的谐波分析法适用于变频电机的铁耗计算。

［1］聂亚林，黄允凯，胡虔生.SPWM供电时电机铁心损耗的研究与测试［J］.电机与控制应用 ，2009，36(10):28-33.

［2］Boglietti A，Lazzar M，Pastorelli M.A simplified method for the iron losses prediction in soft magnetic materials with arbitrary voltage supply［J］.IEEE 2000:269-276.

［3］方瑞明，王榕.基于谐波分析法的高速变频电机铁耗计算方法［J］.电机与控制学报，2004(1):25-27.

［4］GB/T3655—2000，用爱泼斯坦方圈测量电工钢片磁性能的方法［S］.2000.

［5］黄平林.旋转电机铁心损耗的分析与计算［D］.南京:东南大学，2007.

［6］王凤翔.交流电机的非正弦供电［M］.北京:机械工业出版社，1997.

［7］聂亚林，胡虔生，黄允凯.非正弦波供电铁磁材料损耗的研究与测试［D］.南京:东南大学，2008.

［8］上海电器科学研究所.中小型电机设计手册［G］.1994.