单斜臂式悬架刚度与阻尼特性设计计算与仿真

胡甚林 陈辛波

同济大学,上海,201804

0 引言

单斜臂式悬架又称斜置单臂式独立悬架(semi-trailing arm suspension),是介于单横臂式悬架和单纵臂式悬架之间的一种悬架结构形式,单斜臂式悬架中车轮与制动器总成和斜臂固连在一起,因此适用于非转向轮桥或后轮驱动汽车的后桥上。单斜臂悬架的斜臂围绕一根与汽车纵轴成一定夹角的空间轴线摆动,通过适当地布置斜臂旋转轴线的空间位置,可以对车轮上下弹跳时轮距、车轮外倾角、车轮前束角这些参数的变化规律进行调节以获取满意的车辆操控性能。在20世纪80年代一些欧洲汽车制造商就已经将这种悬架形式用在后轮驱动轿车后桥上,并广泛出现在运动型轿车的设计中。此种悬架是一种经典的轿车后悬架结构形式[1]。由于单斜臂式悬架结构简单紧凑,并且弹簧和减振器布置空间上的自由度较大,使用在轮毂电机驱动的微型电动车上可以避免弹性元件与体积较大的轮边电机或减速器发生干涉所带来的布置上的难题。

一般悬架设计中常将悬架机构简化为平面机构进行受力分析与刚度阻尼计算,这种方法存在不够精确、无法准确揭示悬架等效刚度及阻尼系数在车轮弹跳过程中的变化规律的问题。本文将采用空间机构的理论对单斜臂式悬架的运动学特性进行详细的推导,在此基础上进行受力分析,得到悬架等效刚度和阻尼系数与悬架弹性元件和减振器之间的精确关系,并据此编写悬架设计计算程序,可以高效应用于单斜臂式悬架的实际设计过程中。

1 单斜臂式悬架运动学分析

单斜臂式悬架结构以斜臂作为导向元件,通常围绕一根空间轴线运动,如图1所示。悬架斜臂绕空间轴线AB转动,A、B为斜臂与车架之间的铰接点,车轮只有绕车轮轴线旋转的一个自由度,因此可以将其与斜臂视为一个刚体。空间轴线AB的定位关系由斜臂与车身铰接点A在车辆坐标系内位置以及AB轴线在左视图及俯视图上投影与坐标轴之间的夹角来确定。图1中悬架机构在以A为坐标原点、坐标轴方向与车辆坐标系相同且固定在车身上的坐标系 Axyz中定位,则轴线AB在yz平面内投影与y轴的夹角为α,在xy平面内的投影与y轴夹角为β。显然由这两个角度便可以确定AB轴在空间内的位置,而轴线AB在xz平面内投影与x轴夹角为

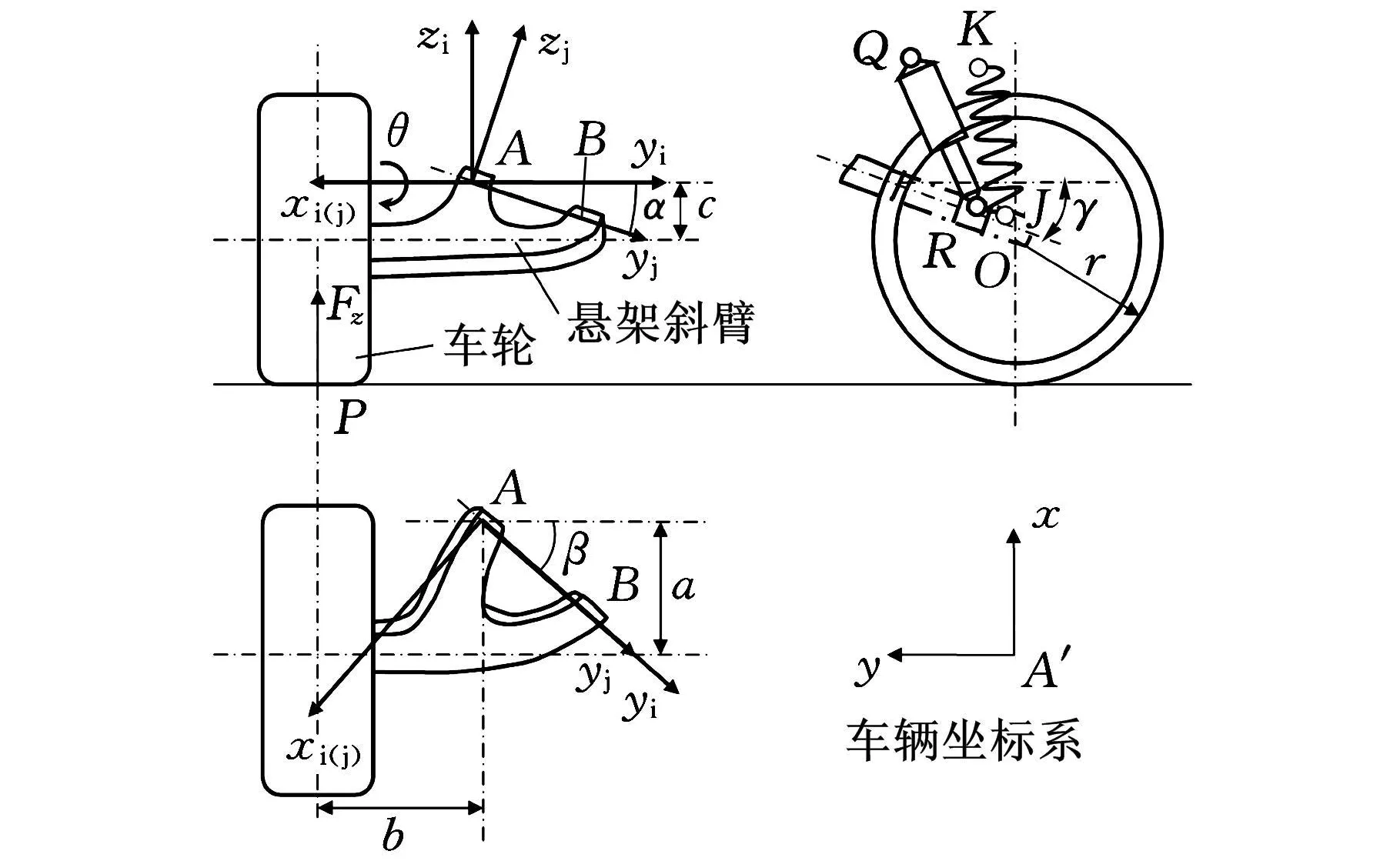
图1 单斜臂悬架机构图

P点为车轮接地点,由图1所示位置关系,静载平衡时P点在Axyz坐标系内的坐标为(-a,b,-c-r),r是车轮半径;O为车轮中心点,坐标为(-a,b,-c)。螺旋弹簧和减振器安装位置K、J和Q、R的坐标分别由减振器和螺旋弹簧的空间布置所决定,其中K、Q为车身上的铰接点,J、R为悬架斜臂上的铰接点。

为了确定悬架斜臂上的点在悬架运动过程中的空间位置,引入坐标系变换方法。

悬架上下跳动时P点在固定的坐标系Axyz里的位置将发生改变,这与斜臂转动的角度有关。弹性元件和减振器与悬架铰接点J、R在Axyz坐标系里的位置也将发生改变,螺旋弹簧和减振器作用力方向亦会产生变化。悬架刚体及车身上任意一点在坐标系 Axyz内的位置矢量可用向量r=(x,y,z)T表示。

如图1中悬架结构俯视图所示,将Axyz坐标系绕z轴逆时针旋转一角度(90°-β)得到以A为坐标原点的另一固定于车身上的坐标系Ax i y i z i,则同一点的坐标在 Axyz坐标系与Ax i y i z i坐标系之间的位置关系为

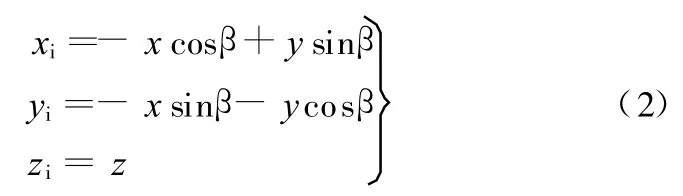
因此可以得到从 Axyz到 Axiyizi的坐标变换矩阵：

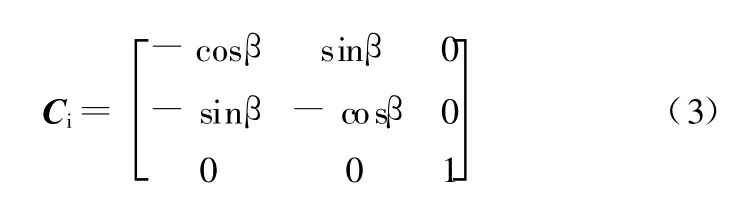
若已知点在 Axyz坐标系内的位置矢量,则可求得其在Ax i y i z i坐标系内的位置矢量：

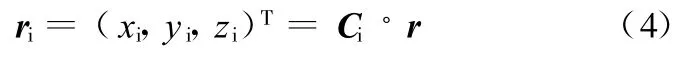
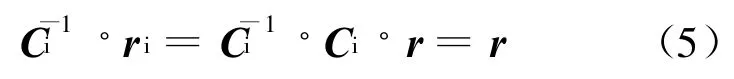
即已知点在Ax i y i z i坐标系内的位置矢量,通过逆变换矩阵C-1i可以得到 Axyz坐标系内相应位置矢量。

将Axiyizi坐标系绕xi轴顺时针转过θ角度后得到一个新的固连于车身的坐标系Ax j y j z j,并且使yj轴与斜臂轴线AB重合。由图2的空间位置关系可以得到坐标系Ax i y i z i转过的角度θ可表示为

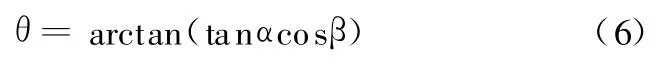
因而可得由Ax i y i z i到Ax j y j z j的坐标变换矩阵C ij：

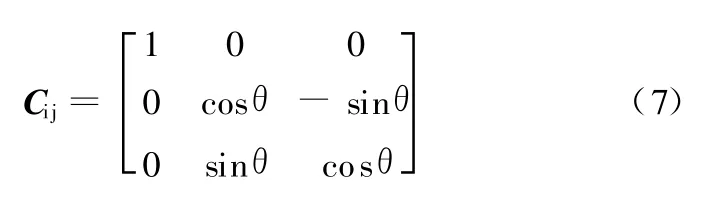
图2 斜臂轴在车身坐标系各坐标平面上的投影

经过两次坐标变换后任意一点在Ax j y j z j坐标系中位置矢量r j为

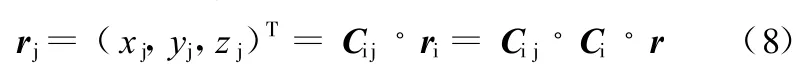
车轮上下跳动时斜臂绕AB轴线转动,因此建立一个与斜臂固连的坐标系Ax k y k z k。当悬架处在静载平衡位置时,固定在斜臂上的坐标系 Ax k y k z k和Ax j y j z j重合,当车轮上下跳动,斜臂绕 AB轴转动,Ax k y k z k相对 Ax j y j z j坐标系会有一个转角φ(图3),相当于将 Ax j y j z j坐标系沿y j轴转动 φ角度得到Ax k y k z k坐标系,可得坐标系变换矩阵：

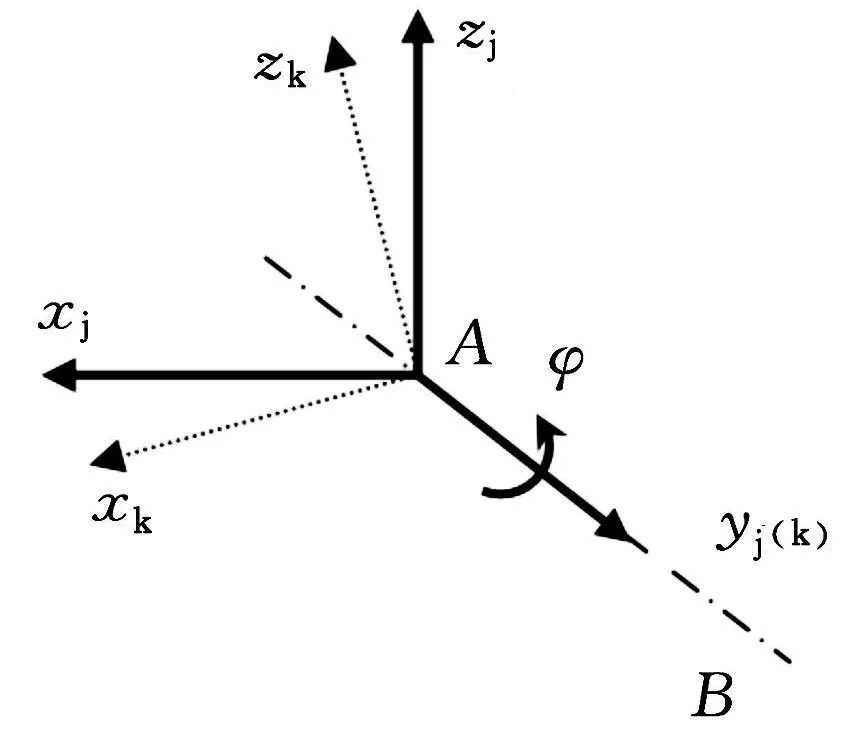
图3 Axj yj zj坐标系变换为Ax k y k z k坐标系

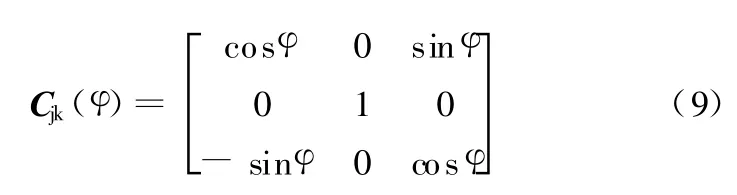
当系统处于平衡位置时,φ=0,因此有

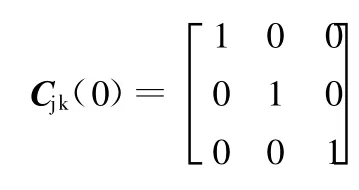
这样可以得到车身上某一点在坐标系Axkykzk内的位置矢量：

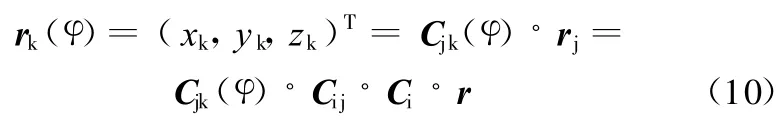
而斜臂上一点在Ax k y k z k内的位置矢量不会随坐标系的转动发生变化：

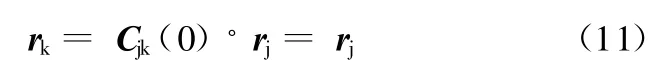
通过以上坐标变换的方式可得出,当斜臂转动φ角度时,斜臂上任一点在固定于车身上的坐标系Axjyjzj、Axiyizi、Axyz中的位置矢量分别为

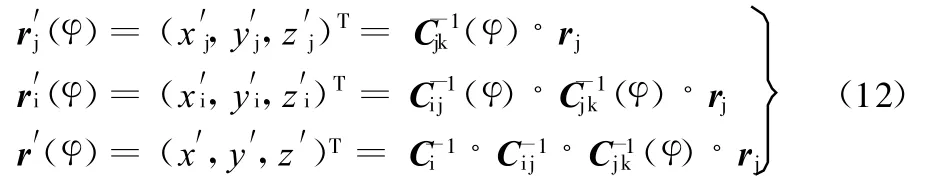
2 悬架等效刚度计算

悬架的等效刚度和簧载质量一起决定了悬架的偏频 f,f是影响汽车行驶平顺性、操纵稳定性以及静载时底盘离地高度的重要参数。悬架等效刚度的定义为车轮接地点受到的地面垂直作用力随车轮垂向位移的变化率。在使用螺旋弹簧作为弹性元件的单斜臂式悬架中,悬架等效刚度会随车轮垂向位移发生改变,呈现出非线性的特点,会对车辆的各种行驶性能产生影响,在悬架的设计中必须考虑到这一因素。下面将对单斜臂式悬架中弹簧刚度和悬架等效刚度之间的换算关系进行推导。

2.1 车轮垂直位移

由悬架几何结构参数得到的车轮接地点P在Axyz坐标系内的位置矢量r P=(-a,b,-cr)T,由式(8)、式(11)得到P点在固定于斜臂上的坐标系Ax k y k z k的位置矢量：

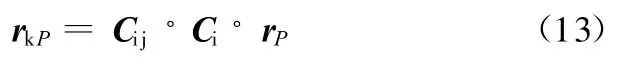
由式(12)得到斜臂绕轴线转动φ角度时P点在Axyz坐标系中的位置为

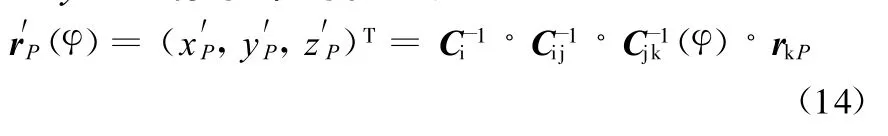
据此便可求出车轮接地点的垂向位移为z′P(φ)。

2.2 悬架受力分析

在悬架受力分析中忽略悬架构件运动时产生的惯性力。

螺旋弹簧在斜臂上安装点R在Axkykzk坐标系中的位置为

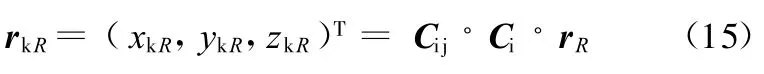
由式(10)得到螺旋弹簧在车身上的安装点Q在Ax k y k z k坐标系中的位置为

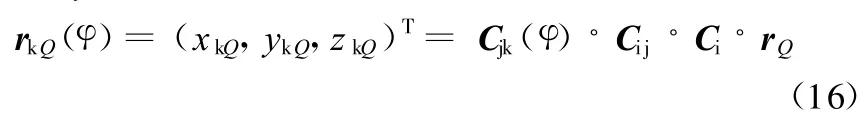
在知道了弹簧安装点Q、R的坐标后就可得到弹簧力在Ax k y k z k坐标系内的表达式：

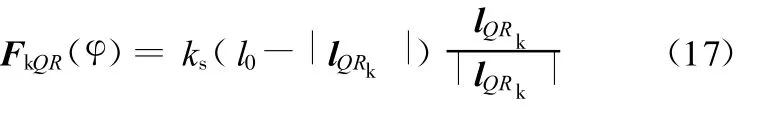
式中,ks、l0分别为螺旋弹簧的刚度和初始长度,是未知量为沿弹簧力作用方向的单位矢量弹簧受压时方向为正。

弹簧力F k QR(φ)在斜臂上的作用点为R,对坐标原点A进行取矩,则力矩矢量为

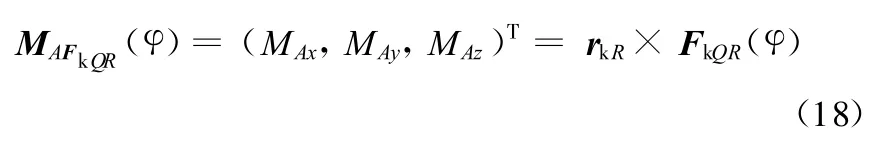
因为斜臂只能绕AB轴转动,斜臂受力平衡时车轮受到地面垂向载荷对AB轴之力矩和弹簧力对AB轴之力矩相等,所以只要知道弹簧力对AB轴的力矩大小MAB即可,而弹簧力FkQR(φ)对A点力矩在y k轴方向的分量即为其对AB轴的力矩大小,因此MAB=MAy。

假设车轮只受地面垂向力的作用,车轮接地点P处受力为F z(φ),悬架在压缩或者伸长行程中地面垂向力大小发生变化(是斜臂摆角φ的函数);当φ=0时悬架处于静载平衡位置,F z(0)等于簧载质量mg。由于Fz方向始终垂直于地面,因此Fz对AB轴的力矩就是Fz到Ayjzj平面的距离(即x′j P)乘上Fz在z j轴上投影长度,方向沿y k轴的负方向。

由以上分析可列出作用在斜臂上的外力对AB轴的力矩平衡方程：

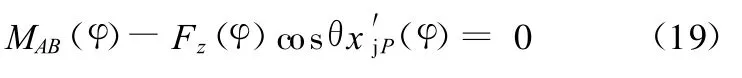
2.3 等效刚度计算

由悬架等效刚度的定义,可得其表达式为

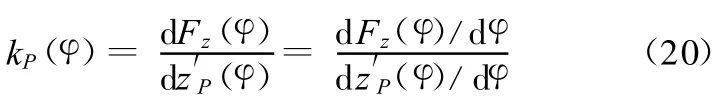
人体所习惯的垂直振动频率约为1～1.6Hz。车身振动的固有频率应接近或处于人体适应的频率范围,才能满足舒适度要求[2],因此在悬架设计时要匹配簧载质量和静载平衡位置处的悬架等效刚度,以保证悬架振动固有频率在合适的范围内。

悬架偏频 f的表达式为

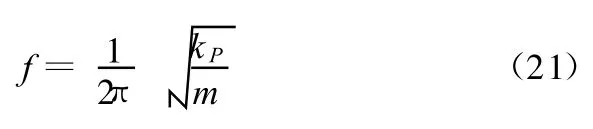
由汽车平顺性所要求的悬架偏频及簧载质量可以得到静载平衡位置处悬架等效刚度为

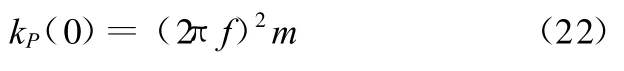
根据受力平衡和等效刚度条件,由式(19)、式(20)可列出以下方程组：

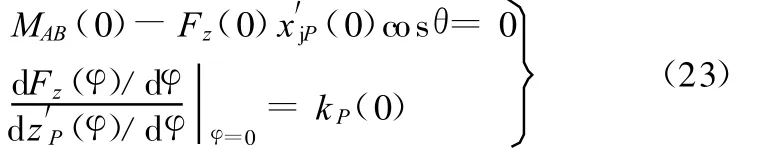
求解式(23)可得弹簧刚度k s和弹簧初始长度l0这两个参数,然后将其代入式(19),可得车轮接地点P处受到的地面垂直作用力Fz与斜臂转动角度φ的关系。

取一系列斜臂转动角度φ计算出相应的F z以及z′P(φ)的值,作垂直反力Fz关于车轮接地点垂直位移z′P的曲线,由曲线的斜率可以得到悬架等效刚度kP关于车轮垂直位移的变化曲线。

3 悬架阻尼系数计算

在悬架性能参数中与汽车行驶平顺性有关的另一参数为悬架阻尼系数。下面对悬架阻尼系数和减振器阻尼系数之间的换算关系进行推导。

由减振器在车身上的安装位置K在Axyz坐标系中位置rK=(xK,yK,zK)T可以得到K点在坐标系Ax k y k z k的位置矢量：

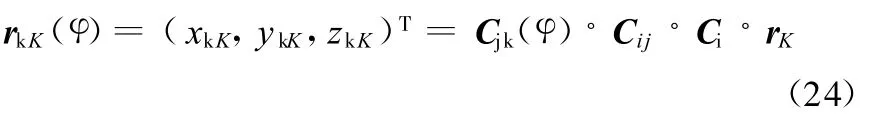
减振器的另一安装位置J固连于斜臂上,因此J点在Ax k y k z k坐标系内的位置为

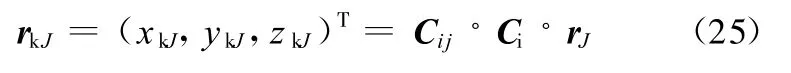
因此减振器长度为

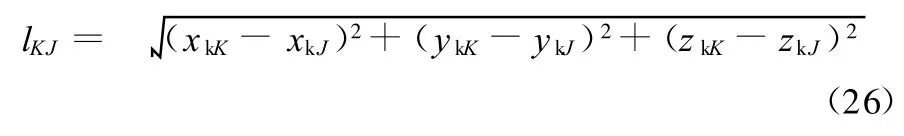
按功能原理,可写出悬架垂向阻尼系数δP与减振器阻尼系数δr的关系[3]：

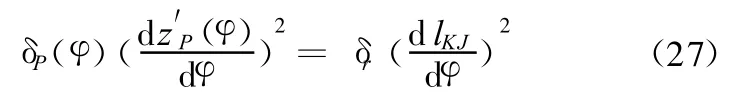
静载平衡位置处的悬架阻尼系数由下式计算可得：

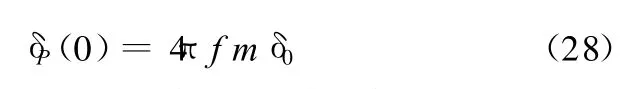
式中,δ0为相对阻尼系数,悬架设计中一般取为0.25～0.5。

得到减振器阻尼系数δr为

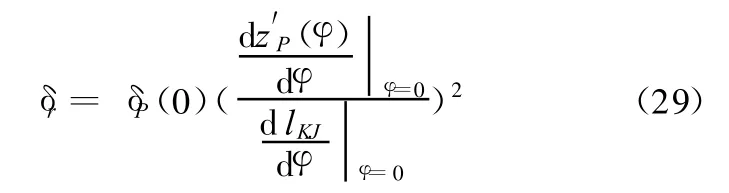
因此,悬架垂向阻尼系数δP关于斜臂转角φ的函数为

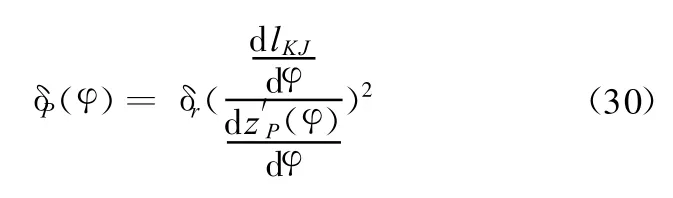
与悬架的等效刚度变化曲线类似,可作出悬架阻尼系数δP关于车轮接地点垂直位移z P的变化曲线,供进一步分析悬架性能使用。

4 计算程序设计

借助于MATLAB软件强大的矩阵和符号计算能力,可以使上述大量空间坐标系变换运算的工作量大为减少,提高设计效率,使得悬架设计中的反复优化成为可能。笔者在以上的推导结果基础上编写了悬架设计计算程序,现简要介绍使用此程序进行悬架设计计算的步骤。

4.1 参数输入

(1)整车性能参数：簧载质量m,悬架偏频f,相对阻尼系数δ0(静载平衡位置)。

(2)由整车布置与悬架性能要求确定的悬架几何结构参数 a、b、c、r、α、β,弹簧与减振器安装位置K 、J、Q、R 的坐标值(图1)。

4.2 悬架弹性元件与减振器参数计算

(1)根据式(14)～式(16)求得P、Q、R点分别在Axyz、Ax k y k z k坐标系中位置矢量的符号表达式。

(2)由平衡位置处的垂向载荷以及悬架偏频设计要求求解式(23),得到弹簧刚度k s和弹簧初始长度l0。

(3)由式(24)、式(25)确定 K、J点在Ax k y k z k坐标系中位置矢量的符号表达式,并得到减振器长度lKJ的表达式。

根据式(29),由平衡位置处悬架阻尼系数确定减振器阻尼系数δr,并由式(30)求得悬架阻尼系数δP的表达式。

4.3 悬架特性仿真输出

根据计算结果,按设定的步长取一系列斜臂转动角度 φ,计算出相应的Fz、δP以及z′P的值,分别作垂直反力Fz与悬架阻尼系数δP关于车轮接地点垂直位移z′P的变化曲线,并计算Fz-z′P曲线斜率,得到悬架等效刚度kP-z′P变化曲线。

5 悬架虚拟样机验证

为了验证计算程序的正确性,在ADAMS软件中建立了同样参数的单斜臂悬架模型,通过对车轮接地点处施加一个垂直位移运动进行仿真,分别得到地面垂直反力Fz、悬架等效刚度kP、悬架阻尼系数δP关于车轮接地点垂直位移的变化曲线,并在ADAMS仿真结果之上叠加计算程序的输出数据。

5.1 地面垂直反力Fz

图4为地面垂向载荷大小与车轮垂向位移的关系。由于仿真时车轮上跳的速度会产生阻尼力,因此仿真过程中将模型中减振器的阻尼系数设为零。

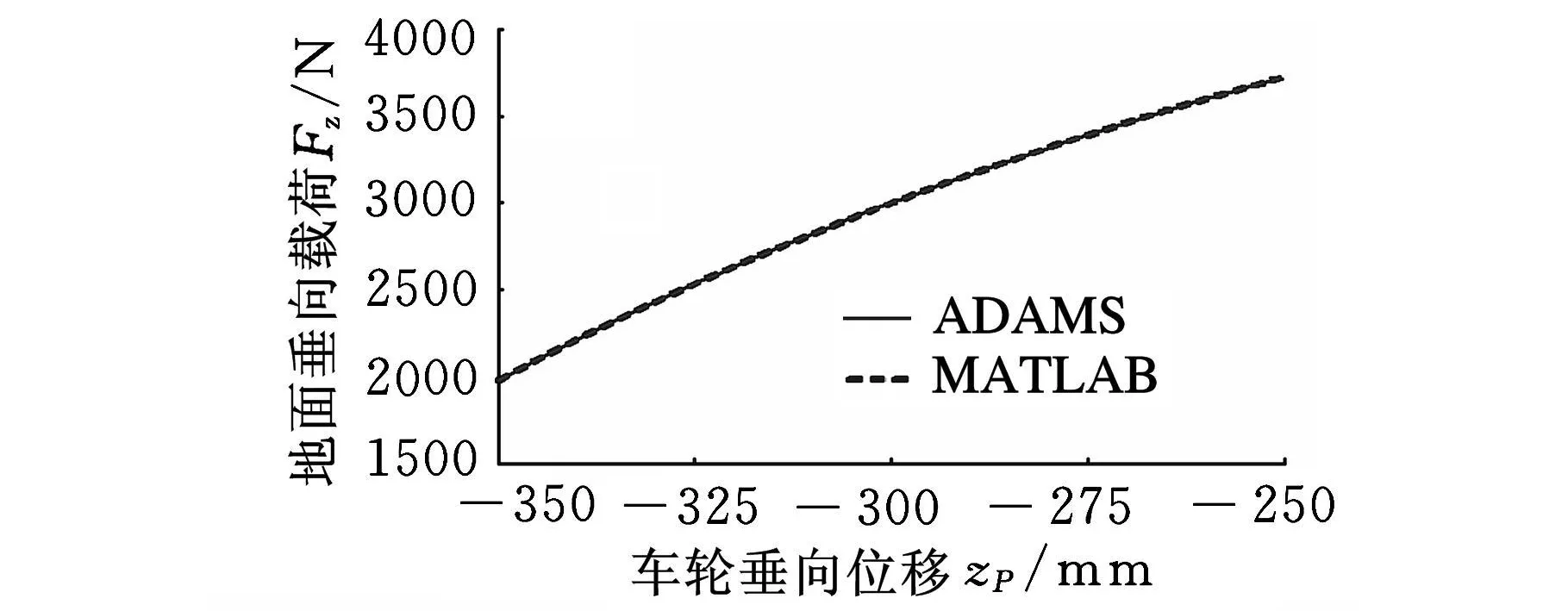
图4 地面垂向载荷大小与车轮垂向位移的关系

5.2 悬架等效刚度kP

对图4中的曲线求斜率,可以获得图5所示的悬架等效刚度变化曲线。

从图5中可以看出,悬架在压缩和伸长行程中刚度会发生明显的变化,即悬架刚度具有非线性特性。

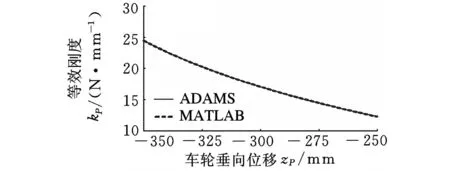
图5 等效刚度kP随位移车轮垂向位移的变化

5.3 阻尼系数δP

为了测出悬架的等效阻尼系数大小,把弹簧刚度设为零,并对车轮施加一个单位速度的垂向运动,测出加载此运动所需要力的大小就是悬架的等效阻尼系数δP。图6示出了阻尼系数δP随车轮垂向位移的变化。

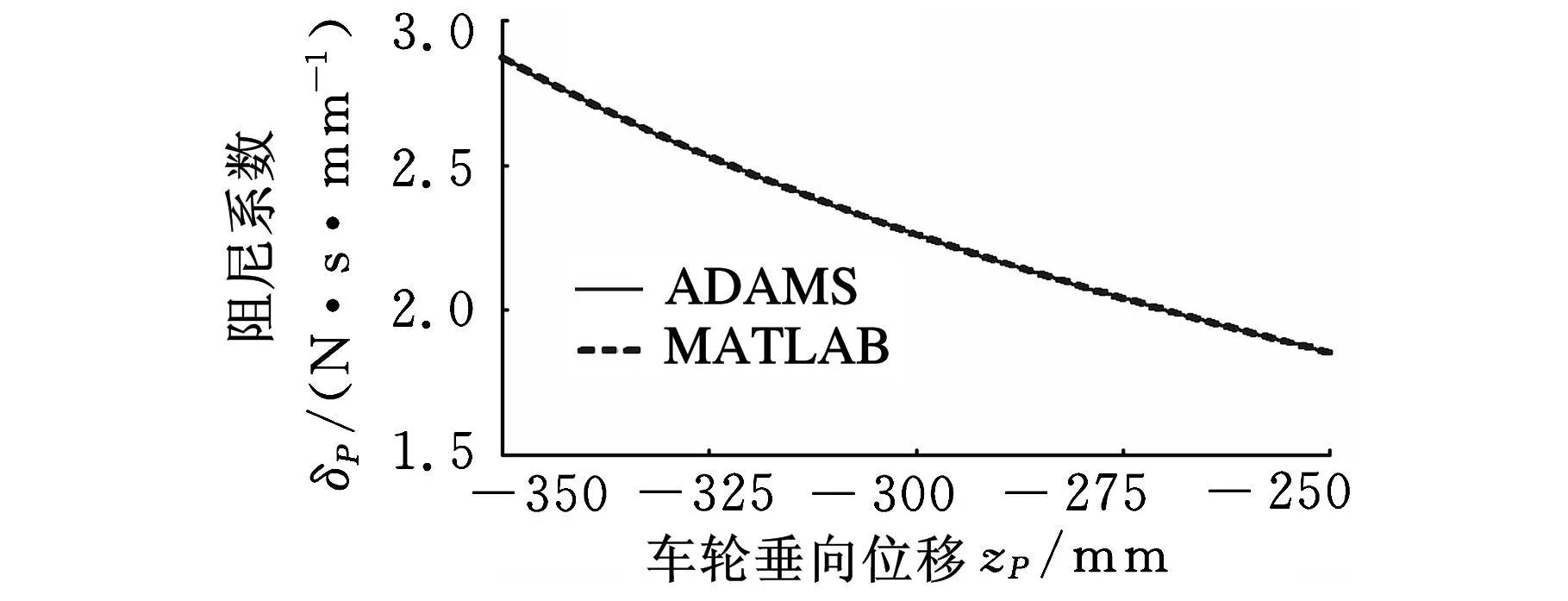
图6 阻尼系数δP随车轮垂向位移的变化

从以上仿真结果可以看出ADAMS软件与MATLAB软件测出的阻尼系数变化曲线完全吻合,证明了悬架设计计算程序输出结果的正确性。

6 结束语

对单斜臂式悬架结构进行了建模,运用空间坐标系变换的手段分析了悬架的运动,对单斜臂式悬架刚度和阻尼系数特性进行了详细的推导,在此基础上使用MATLAB编写了用来计算悬架弹性元件刚度与减振器阻尼系数以及悬架特性仿真的程序,并在ADAMS环境中建立了单斜臂式悬架模型,对MATLAB程序计算的结果进行了验证。本文的工作为此种悬架的实际设计提供了实用的结论与工具。

[1] 野崎博路.サスチューニングの理論と実際[M].东京都文京区：山海堂,2000.

[2] 刘惟信.汽车设计[M].北京：清华大学出版社,2001.

[3] 冯春晟,陈辛波.双横臂-螺旋弹簧悬架受力及刚度阻尼特性非线性分析[J].汽车技术,2007(9)：7-11.