基于多刚体动力学和规则协调的汽车EPS与ASS建模与控制

王其东 秦炜华 陈无畏

合肥工业大学,合肥,230009

0 引言

随着科技的发展,为提高汽车的舒适性和主动安全性,各种动力学控制系统(如EPS(electric power steering)、ASS(active suspension system)、ESP(electric stability program)等)相继应用到了现代汽车上。其中就EPS和ASS两系统来说,由于轮胎侧向力和垂向力的相互耦合,转向系统和悬架系统互相影响,而单独的子系统是仅针对改善某一性能指标而设计的,无法避免其他系统的干扰,因此对于这些系统必须进行集成控制,利用它们的功能互补,更好地提高汽车的稳定性、安全性等综合性能。在系统的集成控制设计中存在两个重要问题——模型的建立和控制策略的确定。

通常,集成控制采用的大多是牛顿力学模型[1-2]。由于汽车是由多构件组成的复杂系统,并具有非线性等特点,而多刚体动力学采用程式化的方法,在解决大型三维机械系统的分析与综合问题上具有一定的优势[3-4]。文献中采用的多刚体模型一般利用汽车动力学仿真软件,如采用ADAMS进行建模[5]。但是在底盘集成控制研究中,涉及多个运动参数,且软件具有封装性,不便对模型进行控制和修改,因此采用人工建立的、能反映系统之间联系、便于施加控制的多刚体模型。对于集成控制策略,通常采用集中式控制[2,6],但其控制器在设计上困难大,设计的周期长,不便于分工协作。而分层-监督式控制策略可尽可能充分地利用原有的控制模块,具有容错处理的能力,可提高系统的可靠性。

1 系统建模

1.1 整车多刚体动力学模型

汽车是一个复杂的多自由度空间运动系统,综合考虑精度和研究的需要,采用多刚体动力学中的笛卡儿坐标系建立简化的装备电动助力转向和主动悬架系统的整车模型。整体坐标系xyz和整车多刚体结构示意图如图1所示。

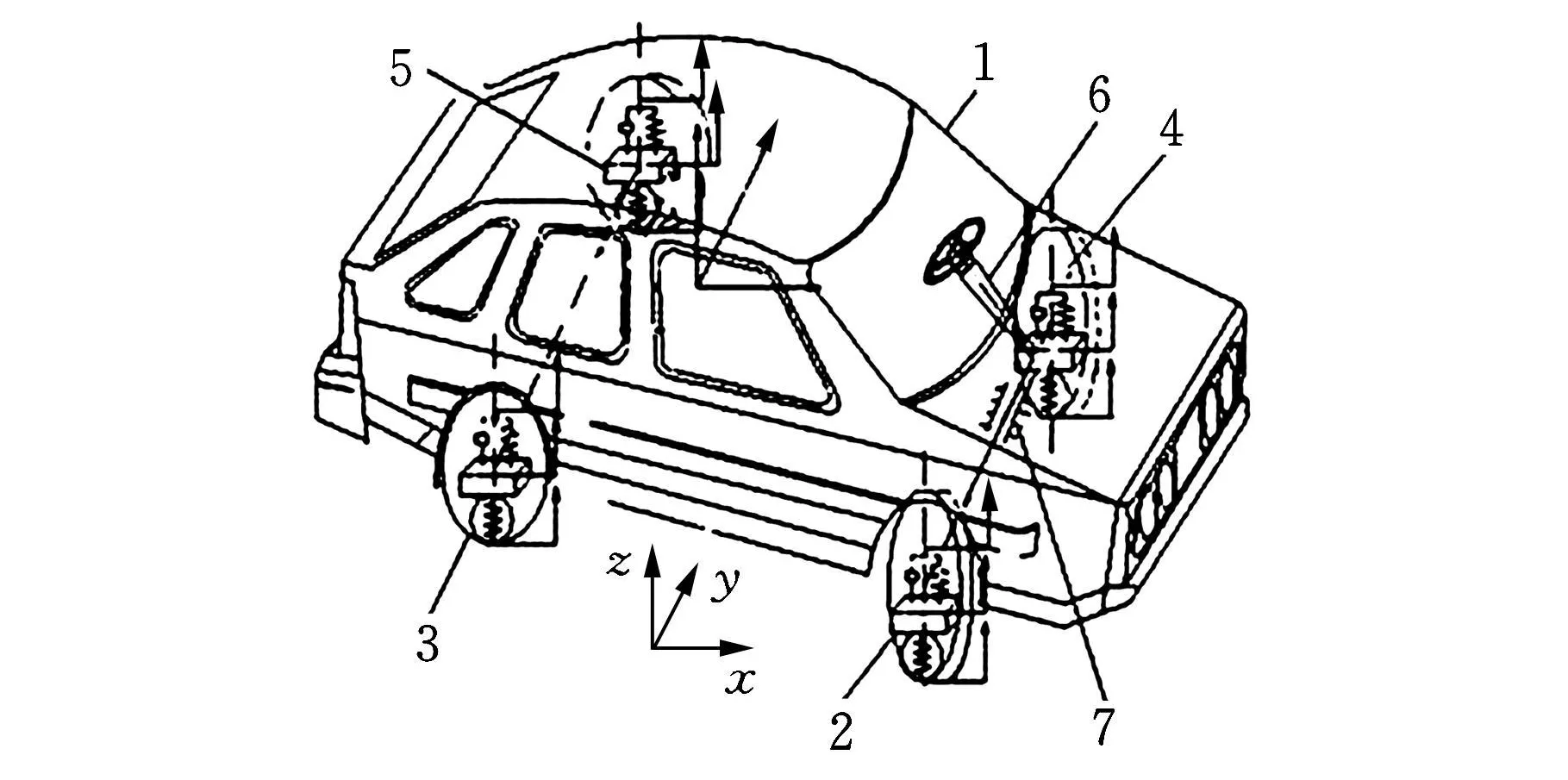
图1 整车多刚体结构示意图

整车由车身、4个车轮组件、横拉杆和转向柱7个构件组成,每个构件的连体坐标系固定在质心处。采用麦克弗逊滑柱式前悬架和纵向拖臂式后悬架,每个前轮组件通过球面-转动复合副和支柱副与车身相连接;后悬架被视作是通过转动副连接在车身的纵摆臂;ASS系统的弹簧-阻尼-可控作用力装置(translational spring-damp-actuator,TSDA)作为多体动力学中的力元素进行建模。连接横拉杆和前轮组件的拉杆模型简化为球面-球面复合副。横拉杆与转向柱通过齿轮齿条副连接。EPS系统的助力矩作用在转向柱上。系统共有34个运动约束方程和7个欧拉参数归一化约束方程。

1.1.1 整车多刚体动力学方程

构件空间广义笛卡儿坐标为

式中,xi、yi、zi为构件的位置坐标;e0i、e1i、e2i、e3i为构件的姿态坐标欧拉四元数。

整车动力学方程[3]为

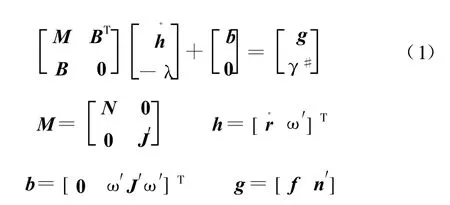
式中,N为构件i的质量矩阵;B为雅可比矩阵,其元素为各约束方程左边的多项式对广义坐标依次求偏导的值,是系统坐标与时间的函数;λ为拉格朗日乘子阵;γ#为加速度方程右项;r为位置坐标;J′为转动惯量,由于车辆对其中心线的对称性,只考虑车身x方向和z方向的惯性积Ixz,其他方向的惯性积近似为零;f、n′分别为作用在构件上的力和力矩,包括转向盘操纵力矩、电动机助力矩、轮胎侧向力和回正力矩、轮胎铅垂力、悬架的TSDA力以及构件的重力和系统内部的摩擦阻力矩;ω′为角速度矢量;ω′为由角速度分量构成的反对称矩阵。

设车身x、y、z三个方向的角速度为(p,q,r),p、q、r分别为侧倾、俯仰和横摆三个方向的角速度。方程展开式中x、y、z三个方向的角速度相互关联,体现了车辆姿态(横摆、侧倾、俯仰)的相互耦合;角速度与欧拉参数之间的运动学方程为

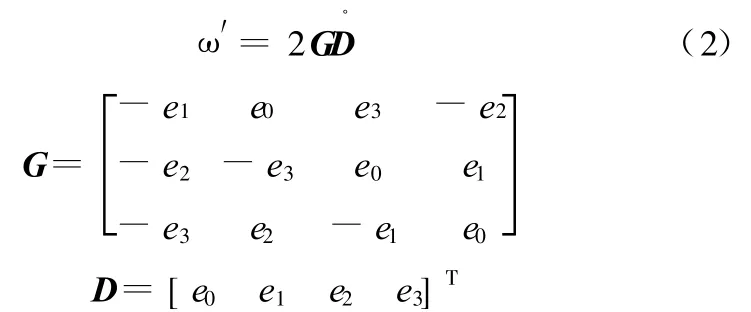
式中,e0、e1、e2、e3为欧拉四元数。

1.1.2 力和力矩

车辆在实际行驶过程中各部件上的受力情况非常复杂,本文根据力的等效作用原理,将实际力系简化为作用于刚体质心的主矢和主矩,轮胎由于自身形变产生的受力被简化为作用于本身的力元。

(1)电动机助力矩。电动机助力矩大小由电动机模型确定,电动机模型计算公式为

式中,it为电动减速机构减速比;Ka为电动机扭矩系数;K b为电动机反电势常数;R0为电枢电阻;U为电动机端电压;δ1为转向小齿轮转角。

(2)悬架TSDA力。设TSDA元件分别连接在两构件的Pa和Pb点,则两点的矢量为

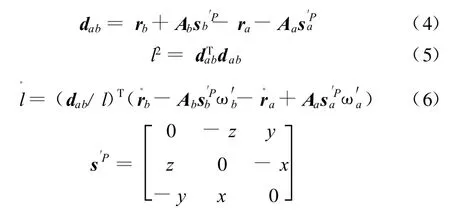
式中,l为TSDA元件长度;ra、rb分别为构件a、b的位置坐标分别为连体坐标系中Pa点和Pb点的位置矢量;分别为中各分量构成的反对称矩阵分别为构件a、b的角速度矢量;Aa、Ab分别为构件a、b的方向余弦阵。

TSDA元件作用在构件a上的广义力为

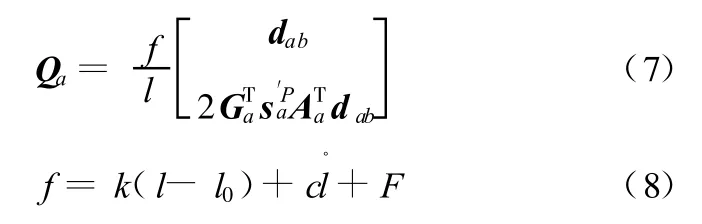
其中等式右边第一项为弹簧力,第二项为阻尼力,第三项为主动悬架可控作用力。

(3)轮胎铅垂力。轮胎铅垂力Qz j的计算公式为

式中,zgj(t)为路面输入;kzj为轮胎垂直刚度;R为轮胎自由半径;zj为轮胎垂直位移。

其中路面输入采用滤波白噪声路面不平度位移时域模型,表达式为

式中,G0为路面不平度系数;wj为均值为零的Gauss白噪声;f0为下截止频率;v为车速。

(4)轮胎侧向力和回正力矩。轮胎侧向力和回正力矩由轮胎模型确定。采用PACEJKA[7]非线性轮胎联合工况模型,其输入为轮胎法向反力、轮胎侧偏角和滑移率,输出为侧向力F y及回正力矩Mz。轮胎模型方程式为

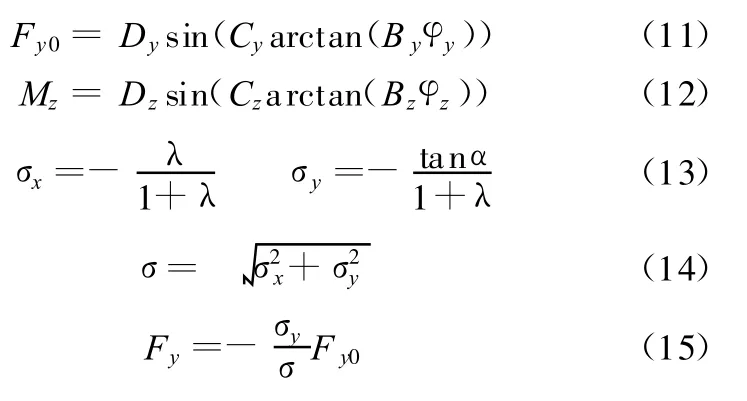
式中,λ为车轮滑移率;α为车轮侧偏角;By、Bz为轮胎刚度因子;Cy、Cz为轮胎模型常数;Dy、Dz为轮胎峰值因子;φy、φz为关于法向力和侧偏角的函数。

多刚体模型中,前后轮侧偏角计算公式为

1.1.3 方程求解

式(1)为非线性微分 —代数混合方程组,处理此类方程组的数值方法有直接法和坐标分离法等。本文采用直接法[3]的算法编程求解,先解式(1)求得,然后根据欧拉参数和角速度之间的关系式计算并对欧拉参数广义坐标和位置坐标进行积分。输入式(1)中各矩阵的具体形式和初始位置、速度条件,即可解得构件的速度以及加速度等状态量的时间历程。

2 控制器设计

设计了EPS、ASS两个子控制器和基于规则的中央控制器。各子控制器又根据不同工况下控制目标的主次设计了两种工作模式对执行器进行控制。中央控制器是一个决策控制器,其功能如下：根据对驾驶员意向的识别,对子系统的监督、检测和对汽车运动状态的观测,给出各子系统两种工作模式间的切换指令,使子系统切入相应的工作模式,达到EPS和ASS两个系统协调控制的目的,以更好地改善汽车平顺性、操纵稳定性等整体控制效果。

2.1 ASS控制器

在直行过程中,ASS针对优化乘适性进行控制;在转向过程中,车身会产生侧倾、横摆等姿态变化,而采用ASS的姿态控制能增强车辆的稳定性。

2.1.1 模式一(以提高平顺性为主要目标)

在该模式,ASS控制器以提高汽车行驶平顺性为目标,控制车身垂直加速度和俯仰角加速度。采用增量式PID控制策略,分别以车身俯仰角加速度偏差和4个悬架上方车身垂直加速度偏差作为输入,输出为控制力 uθ和 u1、u2、u3、u4,叠加得悬架可控力。控制式为

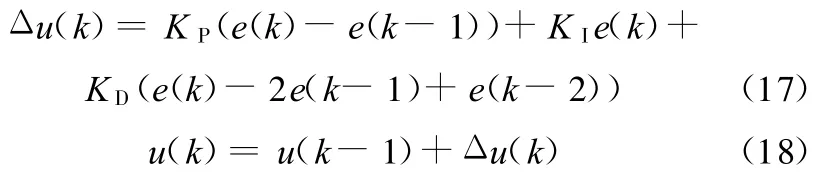
式中,u(k)为可控力;e(k)为控制偏差;k为采样序号,k=0,1,2,…;KP为PID控制器的比例参数;KD为PID控制器的微分参数;KI为PID控制器的积分参数。

其中,前左右悬架可控力[8]分别为

后左右悬架可控力为

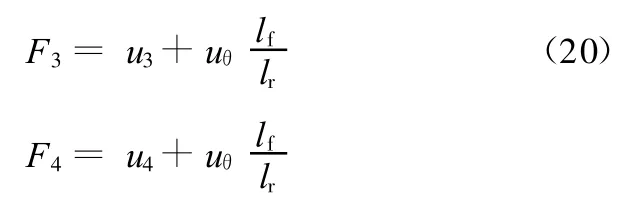
式中,lf,lr分别为前后车轮到车辆质心的距离。

2.1.2 模式二(以控制转向时的车身姿态为主要目标)

在该模式,ASS控制器作为姿态控制器,控制汽车转向工况下的侧倾和横摆,悬架可控力的变化量由基于比例切换函数的滑模变结构控制策略得到。

切换函数为

式中,c为斜率;e为实际值与期望值的偏差。

根据比例切换控制方法,控制率为

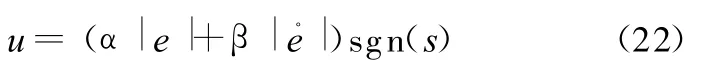
式中,α、β为大于零的常数。

(2)横摆控制：通过调整主动悬架控制力来调节轮胎力,间接产生辅助的稳定横摆力矩。以为输入变量,其中r0为期望横摆角速度;悬架可控力的变化量为输出变量。

期望横摆角速度参考公式[9]为

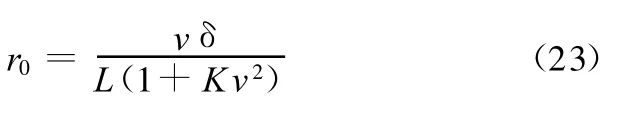
式中,K为车辆稳定性因数;L为轴距;δ为前轮转角。

在多刚体动力学模型中,根据欧拉参数的定义,并假设轮胎是铅垂的,计算式为

式中,e0fl、e0fr为前左右轮的欧拉参数。

在模式二中,考虑到车辆转向行驶工况下,侧倾和横摆相互耦合,因此定义一个加权因子的值根据r和的大小实时确定,此时悬架可控力F′j为

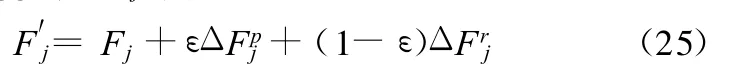
2.2 EPS控制器

汽车在稳态转向时,EPS主要针对转向轻便性进行控制;若汽车进入失稳状态,比如过度转向,此时必须减小助力,削弱驾驶员快速改变前轮转向角的能力,增强路感。

2.2.1 模式一(以改善转向轻便性为主要目标)

在该模式下,EPS控制器采用增量式PID控制策略,控制表达式同式(17)和式(18)。其中控制偏差为目标电流与电动机实际反馈电流的差值,控制器输出为助力电动机电压。目标电流由电动机助力特性曲线确定,如图2所示。

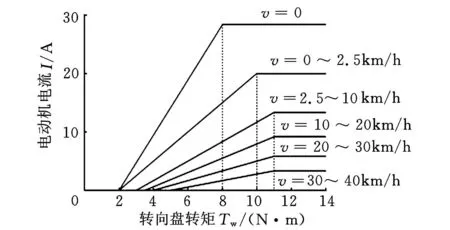
图2 电动机助力特性曲线

2.2.2 模式二(以提高主动安全性为主要目标)

在该模式下,EPS控制器在稳态转向助力目标值的基础上乘以小于1的增益系数,以降低系统的助力矩。

2.3 中央控制器

中央控制器采用基于规则的模糊控制方法,实现各子控制器不同工作模式之间的平稳转换,控制框图如图3所示。规则如下：

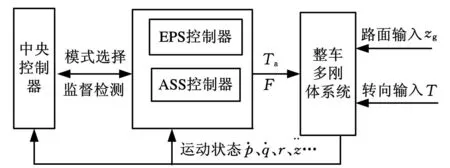
图3 分层-监督式协调控制框图

规则一 直行工况时,ASS控制器以模式一进行控制;EPS系统不工作。

规则二 转向工况时,中央控制器向ASS控制器发出控制指令,转换到模式二进行控制;同时中央控制器根据实际横摆角速度与期望横摆角速度的偏差er(以左转向产生的横摆角速度为正),结合转向盘转角δ的大小识别车辆转向特性。例如车辆左转时,er＞0,车辆存在过度转向现象,中央控制器向EPS控制器发出控制指令,采用模式二进行控制,并确定模式二中增益系数的大小,减小过度转向的趋势,否则指令EPS以模式一进行控制。

3 仿真计算与结果分析

对上述系统,在MATLAB/M文件中编程进行仿真,包括多刚体动力学方程和各控制器的联立求解,主要用到MATLAB的矩阵运算功能、数值积分函数等,其中矩阵运算符“”不需要计算矩阵的逆而直接进行除运算,避免了被除矩阵的奇异性带来的求解问题。某参考车型主要参数见表1。

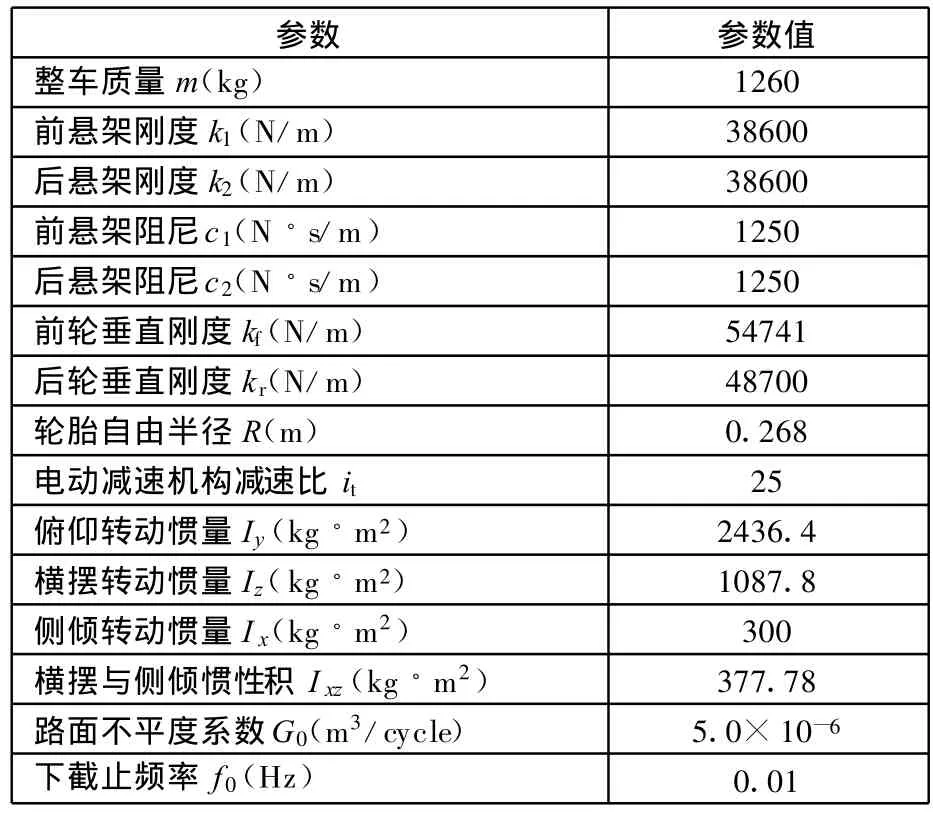
表1 车辆参数

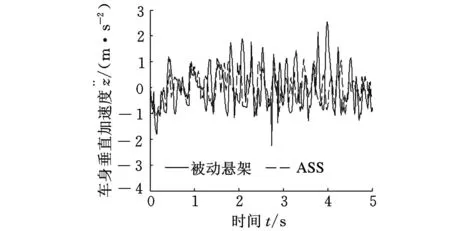
图4 车身垂直加速度

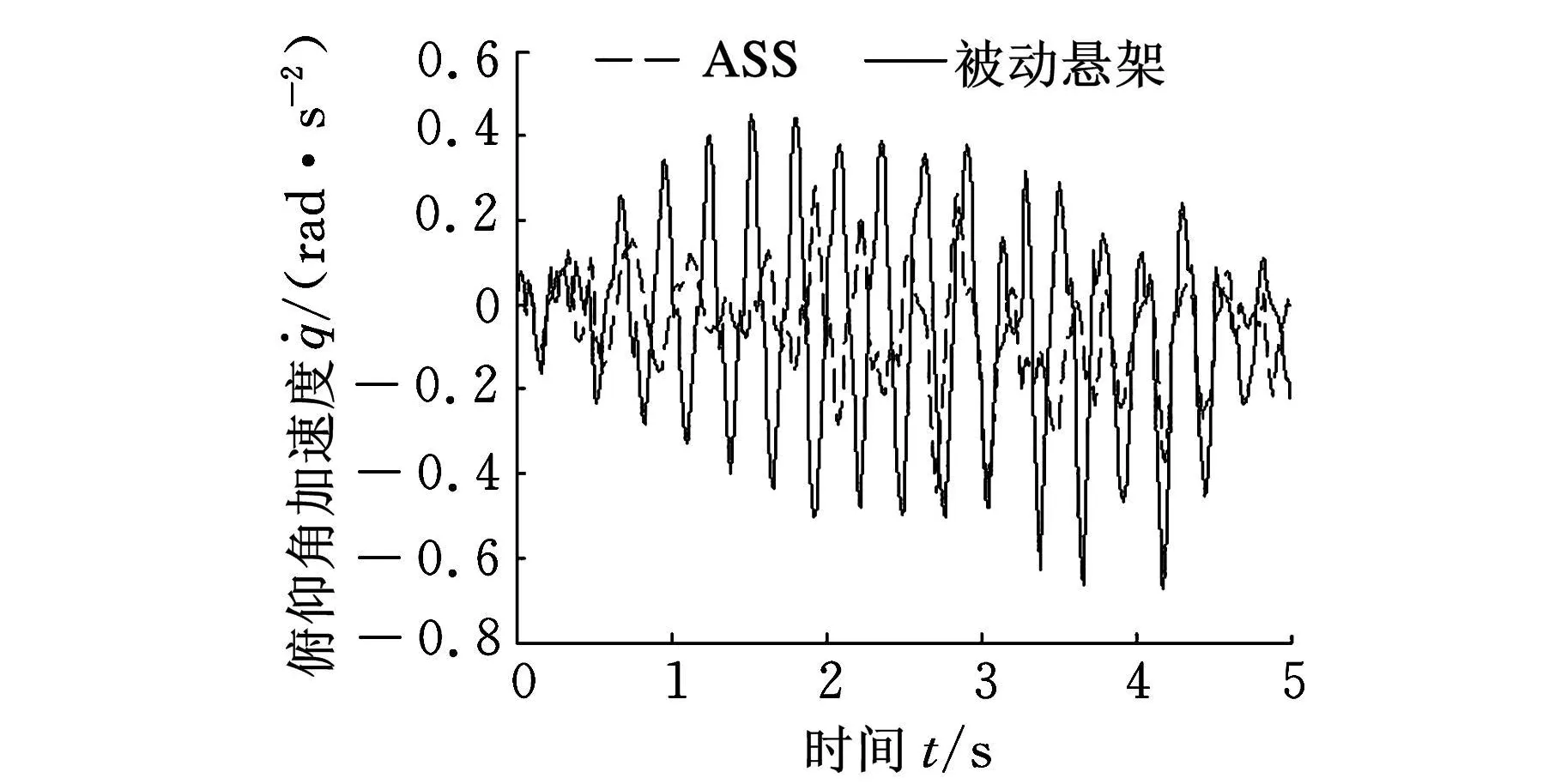
图5 俯仰角加速度

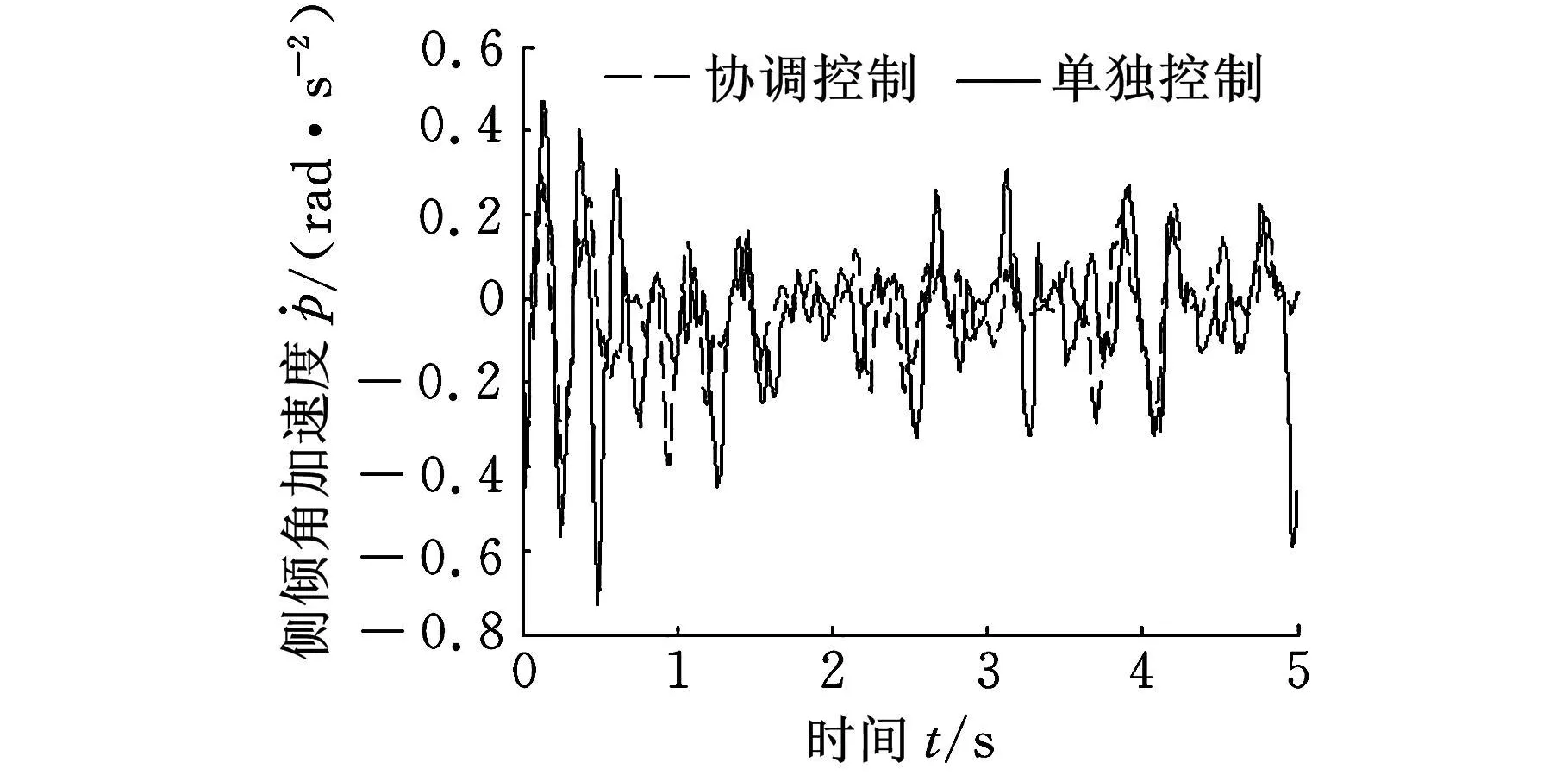
图6 侧倾角加速度

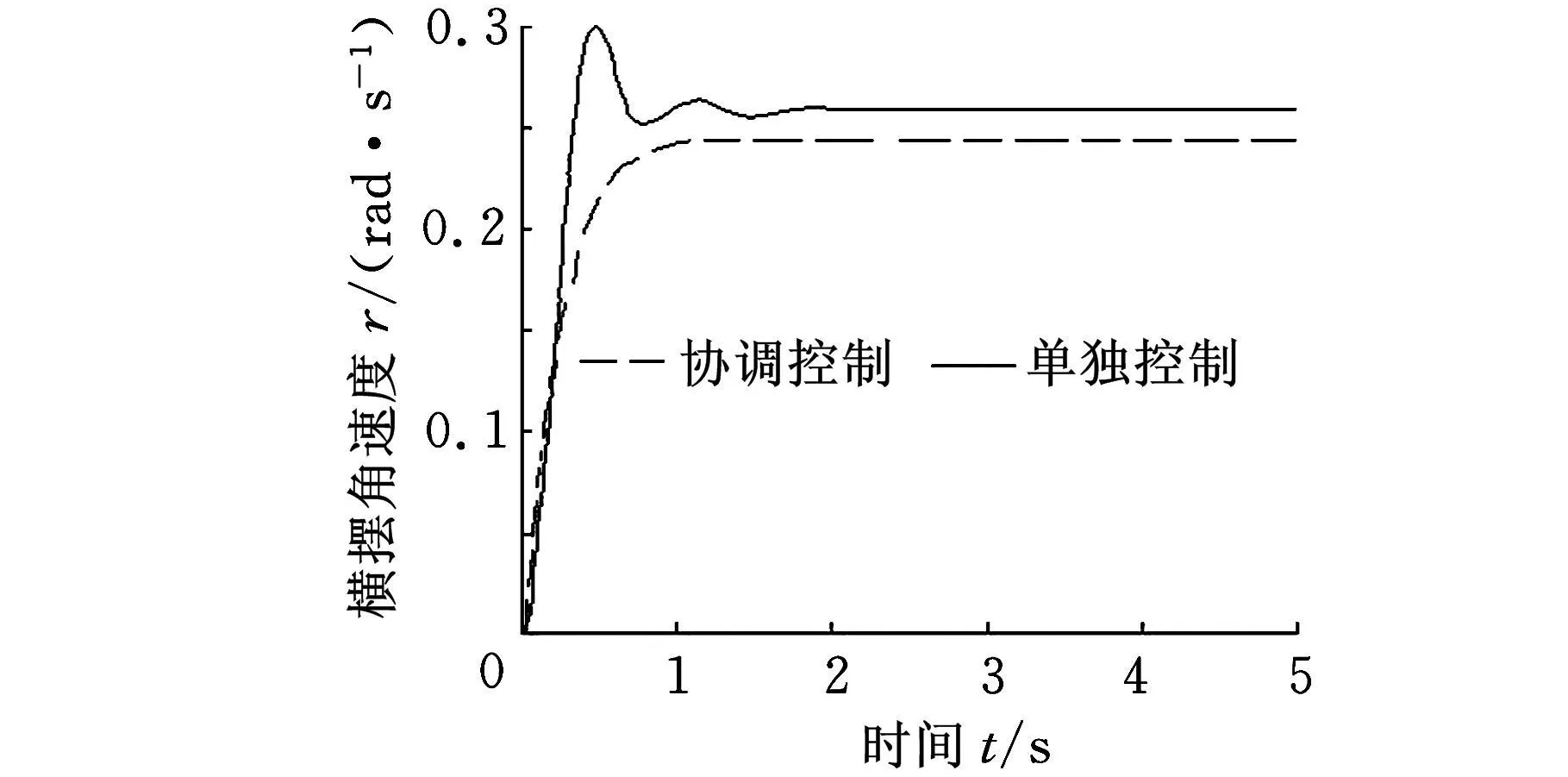
图7 横摆角速度

为了更好地说明协调控制和各个子控制器独立控制时的差异,在工况二下将两系统协调控制和ASS独立控制(指ASS仅用模式一控制)时的侧倾角加速度相对比,仿真结果见图8。协调控制后的侧倾角加速度均方根值从0.0375rad/s2降低到0.0227rad/s2,表明ASS系统参与协调控制时,有效降低了车辆的姿态变化,提高了行驶安全性;将两系统协调控制和EPS独立控制(指EPS仅用模式一控制)时的横摆角速度相对比,仿真结果见图9。协调控制后的横摆角速度波动减小,表明EPS系统参与协调控制时,除了保证转向轻便性,对整车的稳定性也有一定改善。由此可见,EPS与ASS协调控制是有意义的。

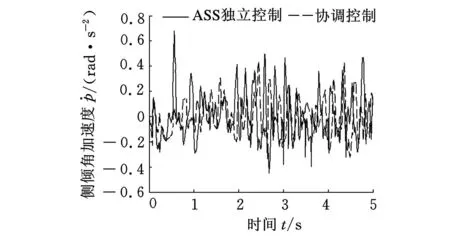
图8 侧倾角加速度

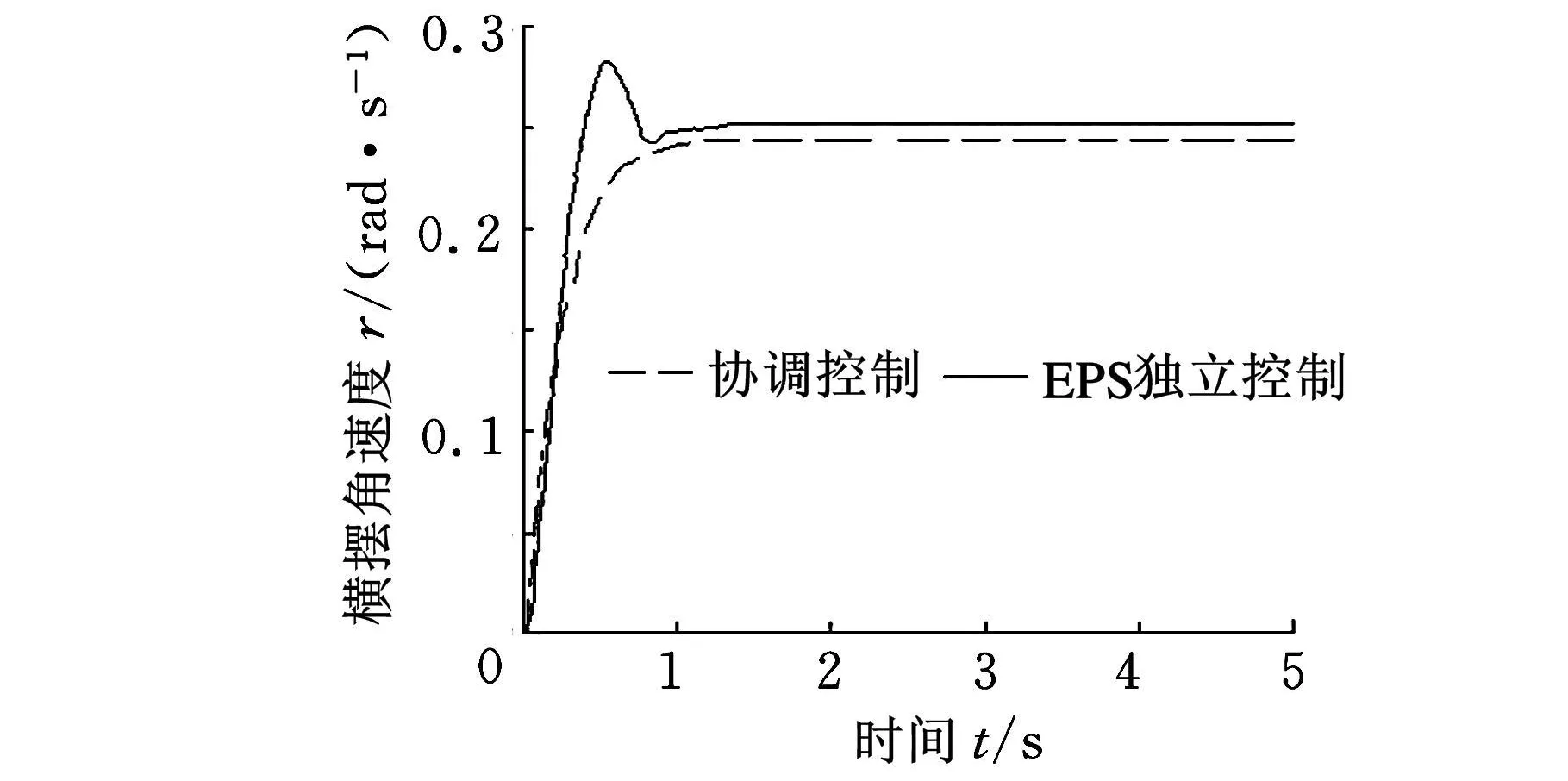
图9 横摆角速度

4 结束语

应用多刚体系统动力学理论建立了整车多刚体模型,在综合考虑ASS与EPS相互影响的基础上,对两系统进行了协调控制研究。仿真结果表明了多刚体动力学模型和分层-监督式协调控制策略运用在汽车底盘集成控制研究中的合理性和有效性。

[1] March C,Shim T.Integrated Control of Suspension and Front Steering to Enhance Vehicle Handling[J].Proc.IMechE,2007,221(4)：377-391.

[2] Cherouat H,Lakehal-Ayat M,Diop S.An Integrated Braking and Steering Control for a Cornering Vehicle[C]//Proe.AVEC04.Amhem,2004：341-346.

[3] Nikravesh P E.Computer-aided Analysis of Mechanical Systems[M].Singapore：Prentice-hall,Inc.,1988.

[4] 王阳阳,靳晓雄,孙海涛.汽车底盘集成控制动力学模型的发展[J].上海汽车,2007(4)：25-27.

[5] 徐中明,余烽,张志飞,等.基于ADAMS和Simulink的车辆转弯制动ABS联合仿真[J].中国机械工程,2009,20(7)：877-881.

[6] Yoshimura T,Emoto Y.Steering and Suspension System of a Full Car Model Using Fuzzy Reasoning Based on Single Input Rule Modules[J].International Journal of Vehicle Autonomous Systems,2003,1(3/4)：237-255.

[7] Bakker E,Nyborg L,Pacejka B.Tyre Modeling for Use in Vehicle Dynamics Studies[J].SAE Paper,870421.

[8] 陈燕虹,刘宏伟,黄治国,等.基于空气悬架客车1/2模型的模糊仿真[J].吉林大学学报,2005,35(3)：25-57.

[9] 余志生.汽车理论[M].北京：清华大学出版社,2000.