基于振动响应场的结构形状优化方法研究

臧献国 于德介 姚凌云

湖南大学汽车车身先进设计制造国家重点实验室,长沙,410082

0 引言

结构在外界激励下会产生振动,不必要的振动会降低结构的性能和使用寿命,通过结构形状优化能有效减小结构振动。结构形状优化设计建立在最优理论和有限元分析的基础上,它是根据给定的设计约束条件,求解满足约束要求且某种结构性能达到最优的结构形状。结构形状优化通过改变结构的形状来改善结构性能和减小结构质量[1],在工程应用领域中占有非常重要的地位。

近来来,国内外学者已在结构形状优化方面作了大量研究。文献[2]选择二维结构边界的一组关键节点坐标构建B样条函数,结构边界上的其他节点和内部节点坐标通过B样条函数插值获取,以应力为设计约束,以质量为设计目标,结合二次规划优化方法和有限元算法对平面结构进行形状优化。文献[3]针对薄壁梁结构有限元模型,以梁截面关键节点为坐标建立了梁截面形状与截面惯性矩的关系,优化了梁截面惯性矩参数。文献[4]利用NURBS曲线定义结构形状,提出了边界曲线的变形能模型,以结构应力为设计约束,通过优化降低了结构的质量。文献[5]提出基于结构边界关键节点的形状参数化方法,结构内部节点通过等参形函数插值获取,能有效优化二维平面结构应力。文献[6]提出了一种等几何结构形状优化方法,通过非均匀有理B样条曲线控制结构形状,将控制点坐标作为设计变量,实现结构边界光滑。文献[7]通过对二维结构边界逐步寻优,结合模拟退火方法优化二维结构的应力,得到了光滑的边界和全局最优解。

在现有的研究工作中,结构形状优化主要集中在结构静力分析领域,以结构动力响应为优化目标和约束的结构形状优化并不多见。结构形状描述方法则广泛基于B样条曲线或曲面,用多项式插值函数描述结构边界,以控制点坐标为设计变量,这对复杂结构来说,会导致设计变量过大或难以对几何形状参数化。针对上述问题,本文建立了基于有限元网格的参数化形状优化模型,提出一种基于振动响应场的结构形状优化方法以控制结构振动。基于振动响应场建立结构形状参数化模型,可减少网格变形失真,形状变化不需要指定扰动方向,能实现结构形状自动寻优。研究了外部激励下的结构振动优化问题,以分析频率带内的最大振动位移为设计目标,将有限元结构坐标的最大变动值及一阶模态频率作为设计约束,利用遗传算法进行优化求解。数值算例表明该方法能有效降低结构振动位移幅值,改善结构动力学特性。

1 结构振动响应的有限元计算

结构有限元的单元质量矩阵和刚度矩阵分别为

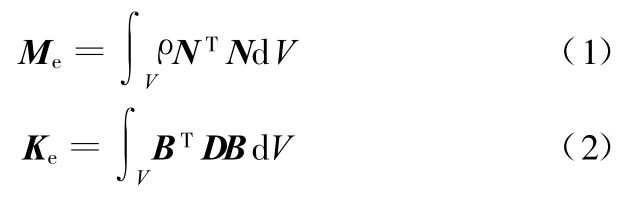
式中,ρ为材料密度;N为单元形函数;D为材料参数本构矩阵;B为应变矩阵。

d V和应变矩阵B与结构几何形状相关。

以等厚的线性四边形壳单元为例,通过坐标映射,等参单元的质量矩阵和刚度矩阵可简化为

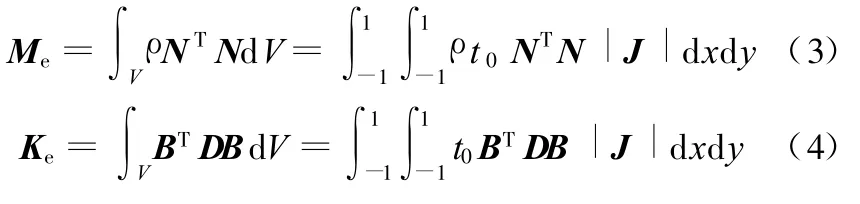
其中,t0为单元的厚度,雅可比矩阵的行列式|J|与结构几何形状相关,单元质量矩阵和刚度矩阵采用高斯积分计算。

单元质量矩阵和刚度矩阵装配后,在外部稳态激励力作用下结构的振动方程为

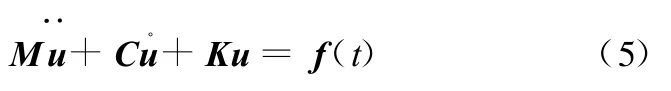
式中,M、C、K分别为结构的质量矩阵、阻尼矩阵和刚度矩阵;u为位移响应向量;f(t)为外力向量。

采用比例阻尼假定,结构阻尼矩阵可表示为

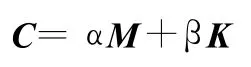
式中,α、β为比例系数。

对式(5)两边作傅里叶变换,得

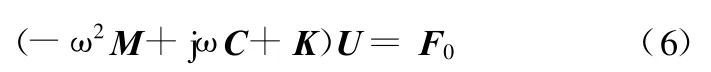
式中,ω为圆频率;U为位移响应向量u的傅里叶变换;F0为外力向量f(t)的傅里叶变换。

从式(6)可求得结构在外力作用下的频域响应。修改结构的几何形状可改变单元质量矩阵和刚度矩阵,从而改变整个结构的质量矩阵和刚度矩阵,进而改变结构在外力作用下的频域响应,因此可通过优化结构形状来改善结构动力学特性。

2 基于振动响应场的形状参数化模型

结构有限元模型形状由各节点坐标决定,为了便于描述有限元的形状参数化,用一个 N维列向量X定义节点的位置,向量包含每个节点的x、y、z方向坐标值,则第i个节点x、y、z方向的坐标值分别对应列向量X第3i-2、3i-1、3i元素的值,用一个n维列向量b定义设计变量,则向量X描述了结构的形状,结构形状可通过一组向量场的线性组合定义,结构形状参数化模型可表示为

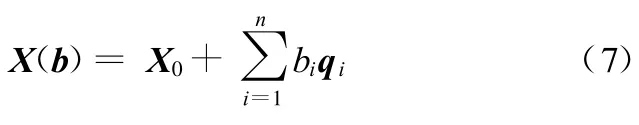
式中,X0为结构初始形状;bi为设计变量为向量场。

若直接以结构修改区域内的所有节点坐标作为设计变量,虽然可以建立形状参数化模型,但由于参数设计变量庞大而无法应用于工程问题,而且会导致有限元网格严重变形而使计算结果失真,故必须寻求一种形状映射函数,以尽可能少的设计变量来描述各节点坐标,建立有效的结构形状参数化模型。

结构振动响应场是在外部激励下的振动分布,根据振动响应的类型可分为位移场、速度场和加速度场。考虑结构在外部宽频动载荷激励下产生频域响应U0,U0是频率的函数,每一频率对应一个振动响应场,振动位移响应场向量包含了每个节点的x、y、z方向的振动响应位移幅值,因此振动位移响应场与结构形状参数化模型中的向量场具有相同维数,可用振动位移响应场作为结构形状参数化模型的向量场。我们采用一组振动位移响应场作为结构形状参数化模型的一组向量场,以振动响应场的系数作为优化设计变量,不同的设计变量可以映射出不同的结构形状。通过对初始结构进行动力学分析,得到结构频域响应U0,在分析频带内选择若干个与振动峰值对应的位移振动响应场作为形状参数化模型的向量场,不同的激励特性可得到不同的向量场。由于位移振动响应场是连续变化的,故采用位移振动响应场可减少形状优化过程中的网格失真变形。

为了便于描述形状改变后几何坐标系下节点新的坐标值,将振动响应场进行归一化,归一化后的振动响应场最大振幅为1。给定一组振动响应场的系数,则对应一种唯一结构形状。每一结构形状下的各节点通过三个方向的坐标描述。以x0和x1表示初始形状和新形状下所有节点在x方向的坐标值、y0和y1表示初始形状和新形状下所有节点在y方向的坐标值、z0和z1表示初始形状和新形状下所有节点在z方向的坐标值,则结构形状参数化模型的节点坐标可以表示为

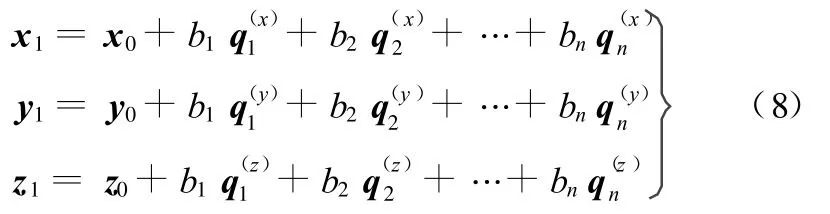
式中,bi(i=1,2,…,n)为选取的第i个振动响应场的系数,即将此系数作为设计变量,取值范围与结构节点坐标波动限值相关分别为选取的第i个振动响应场x、y、z方向的振动位移幅值。

结构节点坐标在x、y、z方向的波动值可以表示为

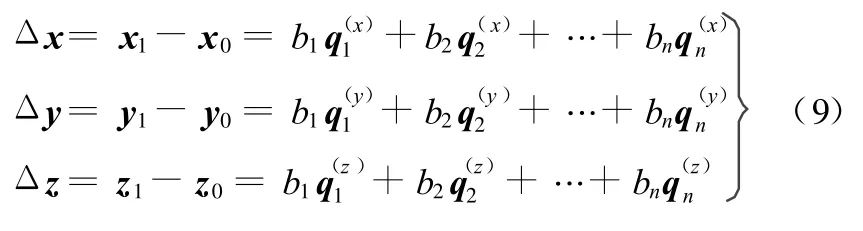
3 结构形状优化

在所分析的频带内,振动响应是频率的函数。以单一固定频率处响应为优化目标无法控制整个频带内的振动响应,甚至可能导致频带内的最大振动峰值增大,而以整个分析频带内的结构振动最大响应值为优化目标则可控制整个频带内的振动响应。为了能获取整个分析频率带内的所有振动峰值,取分析频率步长为1Hz,计算振动响应,识别出分析频带内的最大响应值,则目标函数可表示为

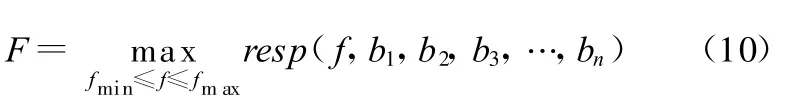
式中,fmin、fmax分别为分析频带的下限频率和上限频率;resp为振动响应(如振动位移、速度或加速度响应);F为目标函数,是设计变量 b1、b2、b3、…、bn的函数。

以最小化振动响应为目标,结构动力学形状优化模型可表示为

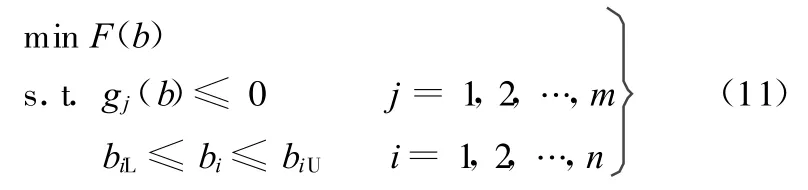
式中,biL、biU分别为设计变量的下限和上限。

遗传算法能在较大的设计变量空间内迅速寻优,有较强的全局优化性能[8],本文采用遗传算法对结构形状进行全局优化。取设计变量bi为遗传算法的群体,目标函数F为遗传算法的适应度函数,选择遗传算法的交叉概率为0.5,变异概率为0.01。

本文方法的流程如图1所示。

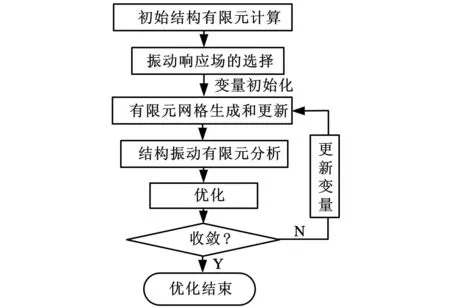
图1 结构形状优化流程图

4 数值算例

四边简支矩形平板,长宽分别为 0.8m和0.4m,板厚为1mm。结构材料性能参数为：弹性模量210GPa,泊松比0.3,密度7800kg/m3。由于在形状优化过程中,结构会变化成空间壳结构,故结构采用四节点四边形壳单元进行计算,共有200个单元,231个节点。板在节点(0.48,0.28,0)(m)位置处作用一个1N的竖向简谐激振力,计算结构激励点的位移响应函数,分析频率为15～300Hz,步长为1Hz,平板的初始形状有限元模型如图2所示。

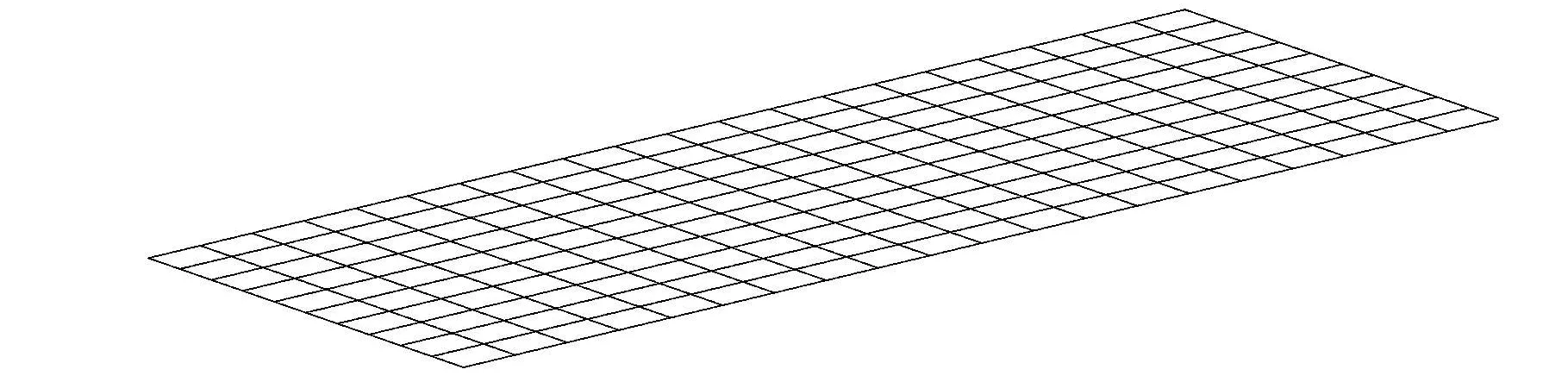
图2 矩形平板初始形状有限元模型

由于平板横向振动主要由板的面外弯曲振动引起,结构节点在面内 x坐标和y坐标的变化对横向振动影响很小,故不考虑。则节点坐标x、y在迭代过程中保持不变,只考虑由节点z坐标引起的结构形状变化,结构形状参数化模型的节点坐标可以简化为

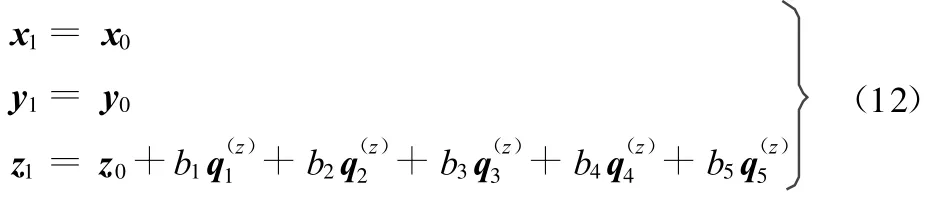
本文以分析频带内加载点最大振动位移响应值作为目标函数,为了提高结构的动态性能,优化后结构一阶模态频率应高于结构初始形状一阶模态频率值,为了保证结构网格单元的质量和结构的可加工性,节点坐标波动值不宜过大,取最大波动值Δz max=10mm,则设计变量范围为0～10即可满足节点波动值要求,该算例的具体优化模型如下：

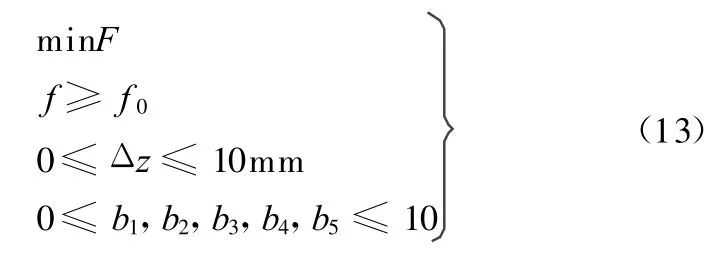
先用有限元计算初始结构的位移响应函数,激励点的位移频率响应函数如图3所示,位移频率响应曲线的前5个峰值对应的频率分别为19Hz、30Hz、49Hz、65Hz、76Hz,选取这 5 个频率处的结构位移振动响应场作为形状参数化模型的一组向量场。

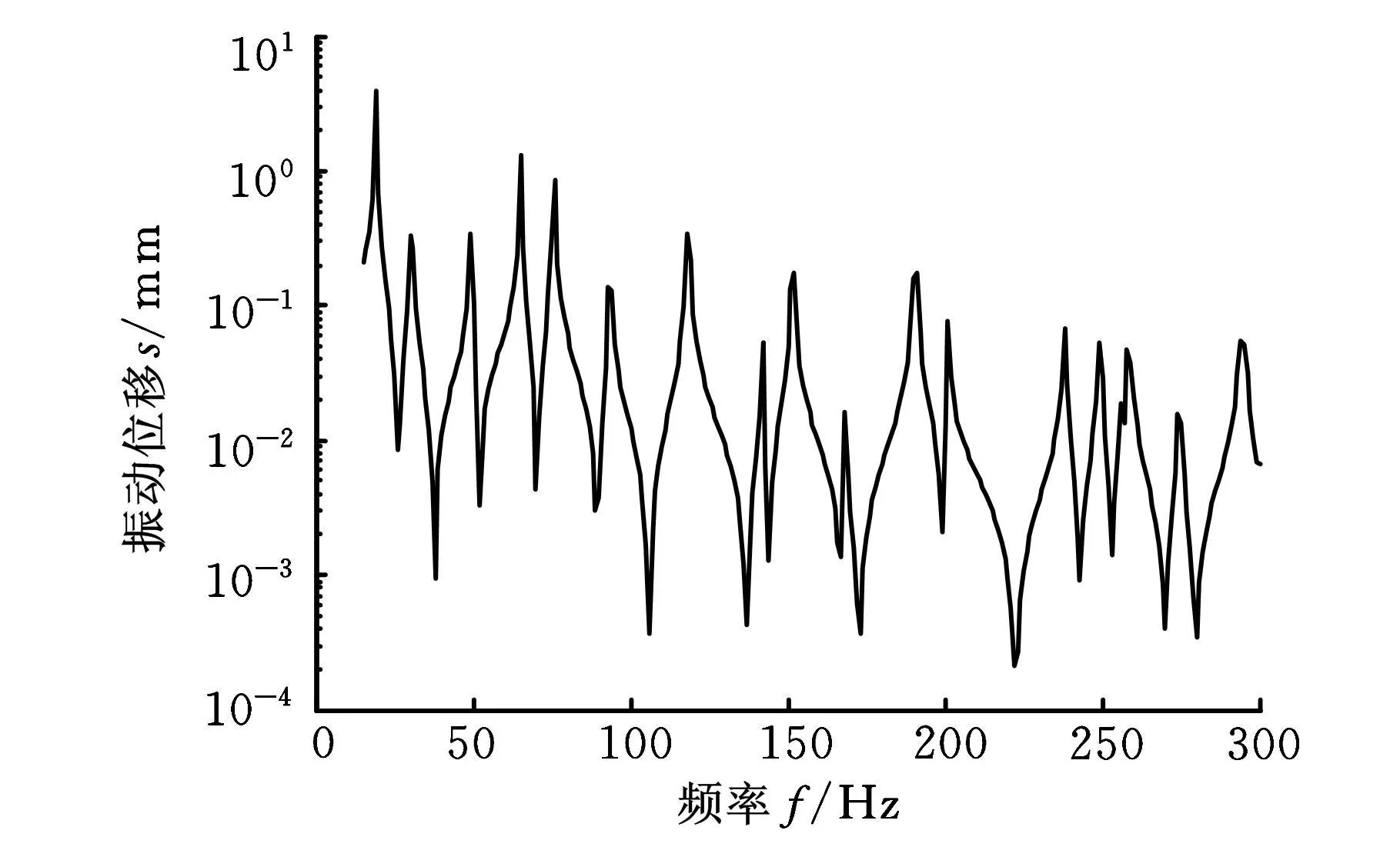
图3 矩形平板初始形状激励点位移频率响应曲线

图4 平板优化后形状有限元模型

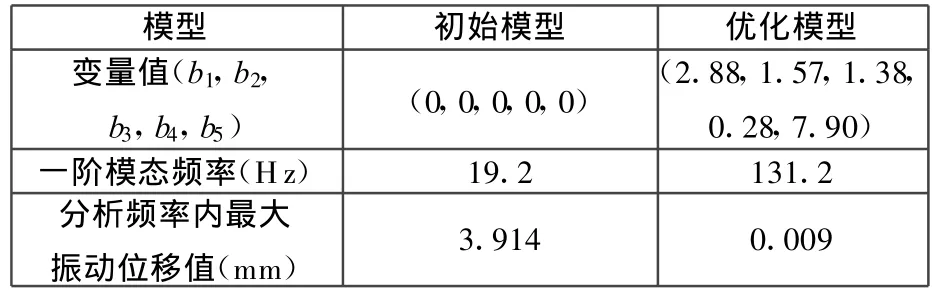
表1 优化前后各参数结果对比

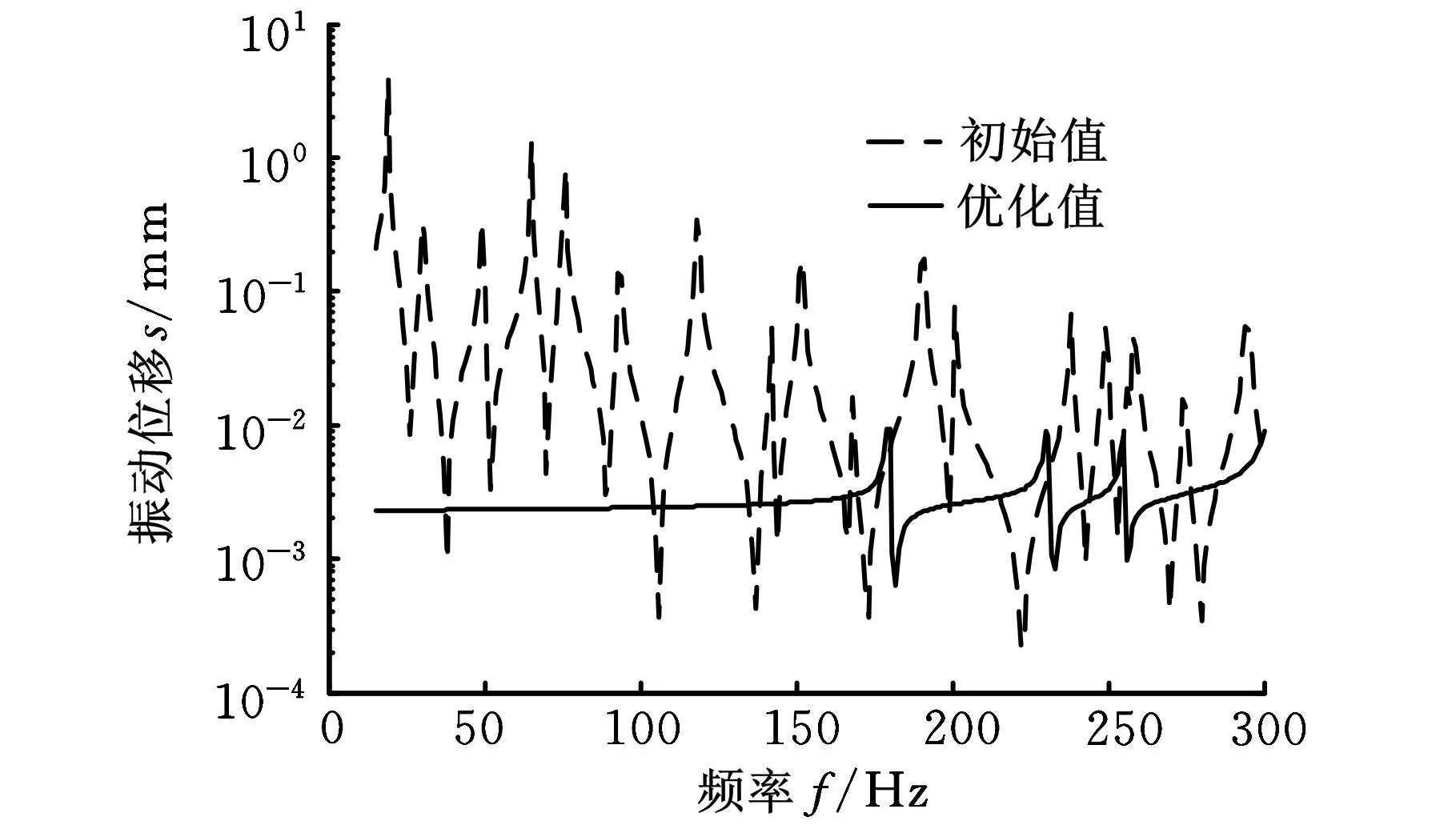
图5 优化前后振动位移对比

5 结论

结构形状优化设计是一种有效改善结构动力性能的方法,本文将形状参数化模型、有限元分析和遗传算法相结合,提出一种基于振动响应场的结构形状优化方法。与B样条曲线、Bezier曲面和多项式插值参数化形状优化方法相比,本文方法具有如下特点：能减少有限元网格变形失真;可用更少的设计变量映射结构形状;形状的变化不通过几何控制点移动实现,而是通过向量场的系数变化实现;不需要指定扰动方向;优化设计变量与结构位移响应场的选取个数有关,与结构的复杂程度无关等。数值算例表明采用一组结构振动位移响应场作为结构形状参数化模型的向量场是可行的;用本文方法进行结构形状优化设计能有效改变结构形状,降低结构的振动位移幅值,改善结构的动力学特性。

[1] Mackerle J.Topology and Shape Optimization of Structures Using FEM and BEM：a Bibliography[J].Finite Elements in Analysis and Design,2003,39(3)：243-253.

[2] Hyun S,Kim C.An Efficient Shape Optimization Method Based on FEM and B-spline Curves and Shaping a Torque Converter Clutch Disk[J].Finite Elements in Analysis and Design,2004,33(13)：1803-1815.

[3] Vinot P,Cogan S.Shape Optimization of Thinwalled Beam-like Structures[J].Thin-walled Structures,2001,39(7)：611-630.

[4] Wang Xuelin,Zhou Ji.A Physics-based Parameterization Method for Shape Optimization[J].Computer Methods in Applied Mechanics and Engineering,1999,175(1)：41-51.

[5] Song X,Baldwin J D.A Novel Node-based Structural Shape Optimization Algorithm[J].Computers&Structures,1999,70(5)：569-581.

[6] Wolfgang A W,Moritz A Z,Chirstian C.Isogeometric Structural Shape Optimization[J].Computer Methods in Applied Mechanics and Engineering,2008,197(33)：2976-2988.

[7] Frazil O S.Shape Optimization of 2D Structures Using Simulated Annealing[J].Computer Methods in Applied Mechanics and Engineering,2007,196(35)：3279-3299.

[8] Woon SY,Querin O M,Steven G P.Structural Application of a Shape Optimization Method Based on a Genetic Algorithm[J].Structural and Multidisciplinary Optimization,2001,22(1)：1615-1488.