一种基于神经网络算法的非线性PID控制器

李桂梅，曾喆昭

(1. 湖南商学院 计算机与电子工程学院，湖南 长沙，410205；2. 长沙理工大学 电气与信息工程学院，湖南 长沙，410076)

随着系统复杂程度的提高和对象不确定性因素的增多，传统的PID控制已经不再适用，而非线性PID控制能真实反映控制量与偏差信号之间的非线性，在一定程度上克服了线性PID控制的缺陷。近10年来，国内外许多研究者将非线性特性引入PID控制器的设计[1-9]。目前，由多种方式合成的非线性 PID控制器主要有模糊系统[10]、人工神经网络[11]以及基于经验式的非线性函数设定[1-7,9,12-13]等。从原理上说，非线性特性的引入可以为控制过程带来许多益处，如补偿被控对象的非线性、改善控制性能、提高控制系统的鲁棒性等，为控制器的设计提供新的自由度，但在理论与应用研究中较复杂[9]。在这种情况下，研究一种设计简单、使用方便的非线性PID控制器具有重要的理论意义和应用价值。基于经验式的非线性函数设定方法是使常规PID控制器的比例增益系数Kp、积分增益系数Ki和微分增益系数Kd成为偏差信号e(t)的非线性函数，即 Kp(e(t))，Ki(e(t))和 Kd(e(t))，然后，以这 3个函数来代替常规PID控制器的3个增益系数。尽管以偏差信号作为生成非线性函数 Kp(e(t))，Ki(e(t))和Kd(e(t))的依据，但生成过程究竟符合什么样的规律并没有固定的公式可利用，这正是建立非线性PID控制器模型的关键。要得到非线性函数Kp(e(t))，Ki(e(t))和Kd(e(t))的准确解析式很复杂，在此，本文作者通过分析常规PID参数随系统过渡过程误差变化的理想变化关系[14]，分别给出比例、积分和微分增益参数关于误差的动态非线性函数，从而获得非线性 PID的可用模型。

1 非线性PID控制器模型

Kp，Ki和Kd3个参数随误差e(t)变化的关系曲线如图1所示[14]，这些曲线揭示了Kp，Ki和Kd3个参数在PID控制过程中的作用和物理意义。

图1 PID 3个增益参数随误差的变化曲线Fig.1 PID gain parameters of three curves with error

(1) Kp的作用是减小超调，增加快速性，因而要求当误差|e(t)|较大时，Kp也较大；当|e(t)|较小时，Kp也较小。可由图1构造Kp关于误差e(t)的动态非线性函数为

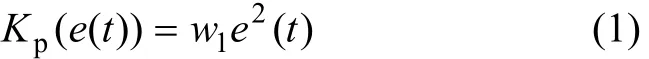
(2) Ki的作用是累积系统误差，以减小系统静态偏差，因而，要求当|e(t)|较大时，Ki较小；当|e(t)|较小时，Ki较大，其物理意义明确，可由图1构造Ki关于误差e(t)的动态非线性函数为：

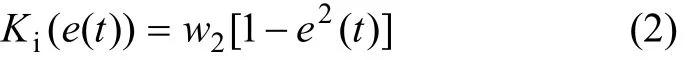
这里要特别指出的是：当出现积分饱和情况时，通过系数w2的自适应调整可有效避免积分饱和的情况。

(3) Kd的作用是增加系统阻尼，对系统起到提前校正、达到提高系统稳定性的目的，因而要求超调(e(t)＜0)越多时，Kd越大；欠调(e(t)＜0)越多时，Kd越小；在稳定值附近(e(t)≈0)时，Kd介于超调和欠调时的之间。因此，可由图1构造Kd关于误差e(t)的动态非线性函数为

从形式上看，式(1)～(3)都是关于误差信号e(t)的二次函数，但是，由于系数w1，w2和w3都是动态系数，因此，由式(1)～(3)构造的非线性函数具有高度非线性，最终得出的动态非线性PID模型为：

将式(1)～(3)代入式(4)，经整理得：

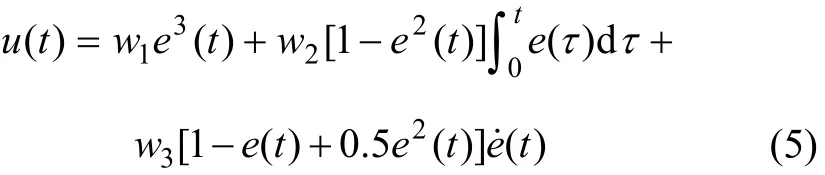
为了便于CPU处理，将式(5)离散为

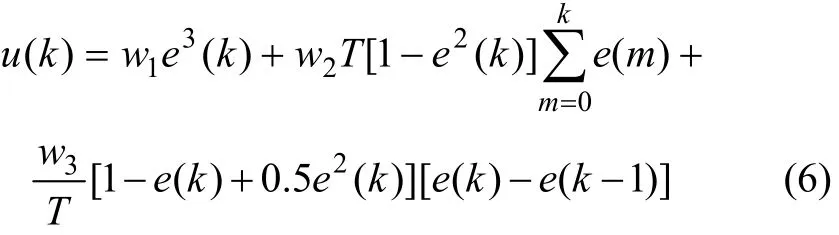
其中：T为采样周期，是1个常数。将T分别隐含到系数w2和w3中，并设

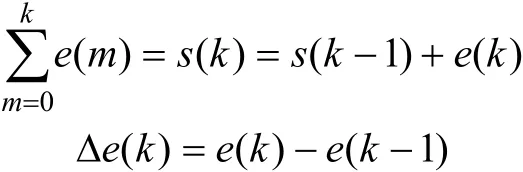
则式(6)可简写为

i22微分项为

式(7)所示的非线性控制率给出了明确的物理意义：在超调(e(k)＜0且e(k)→ -1)时，非线性PID控制器主要由非线性比例项和非线性微分项起决定作用，而非线性积分项的作用很小；在欠调(e(k)＞0且e(k)→1)时，主要由非线性比例项起决定作用，而非线性微分项和积分项起的作用很小；在稳定值附近(|e(k)|较小)时，主要由非线性积分项、微分项起决定作用，而非线性比例项的作用很小。这在很大程度上保证了系统在过渡过程中PID参数随误差变化的理想变化关系。

2 动态非线性 PID神经网络控制器模型算法

2.1 动态非线性PID神经网络控制器模型

由式(7)可知，若以]1,1[)(-∈ke和u(k)分别为神经网络的输入和输出，并以动态系数w1，w2和w3为网络权值，以非线性函数 e3(k)，[1-e2(k)]s(k)和[1-e(k)+0.5e2(k)]Δe(k)为隐层神经元激励函数，则可得到网络拓扑结构为1×3×1的动态非线性PID神经网络控制器，其模型如图2所示。其中：s1(k)=e3(k)；s2(k)=[1-e2(k)]s(k)； s3(k)= [1-e(k)+0.5e2(k)]Δe(k)； s(k)=s(k-1)+e(k)；s(-1)=0；Δe(k)=e(k)-e(k-1)，e(-1)=0。

动态非线性 PID神经网络控制器模型如图 2所示。由图2可知：本文研究的动态非线性PID神经网络控制器不仅保留了常规 PID控制器结构简单的特点，而且构造了PID增益参数关于误差信号的动态非线性函数。因为w1，w2和w3是动态权值，因而实现了PID增益参数的高度非线性，并将其分别融入到3个隐层神经元中，通过神经网络的实时在线训练来获取权值系数，有效避免了常规神经网络控制器隐层神经元节点数难以确定的问题。

2.2 动态非线性PID神经网络控制器算法

由图 2可知，系统初始误差函数为：E(k)=r(k)-y(k)，通过比例阈值函数可得归一化误差信号e(k)(非线性PID神经网络智能控制器的输入信号)为

定义性能指标为：

其中：

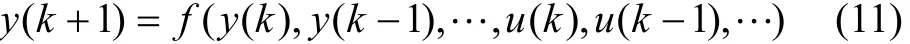
作为一个整体，通过对神经网络输出u(k) (见式(7))表达式中的权值系数的优化，使性能指标J最小。采用最速下降法，网络权值训练算法如下：

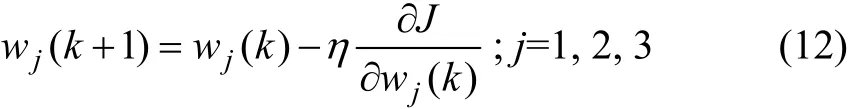
由式(7)～(11)可得：

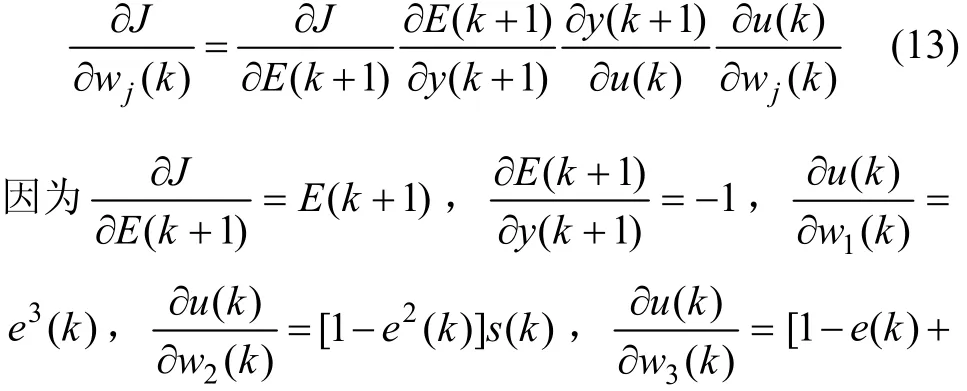
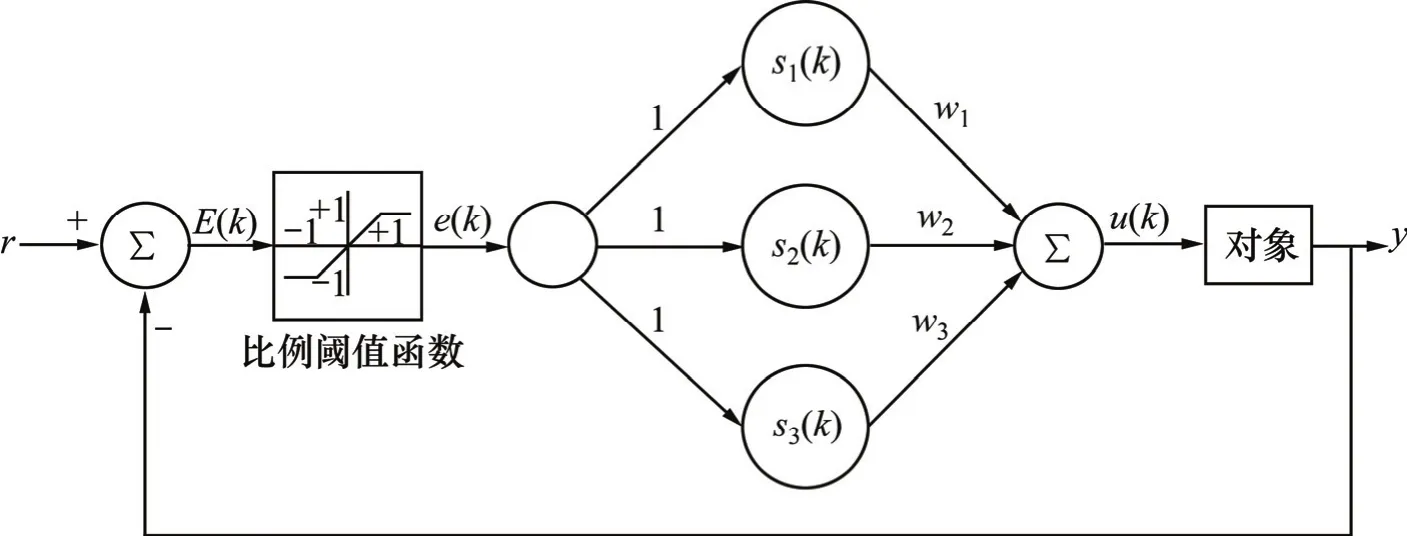
图2 动态非线性PID神经网络控制器模型Fig.2 A controller model of dynamic nonlinear PID neural network

2.3 非线性PID神经网络算法

由 式(17)～(19)可 知 ： E ( k+1)和 yu(k)=均与系统的未来输出y(k+1)(未知)有关，因而，神经网络权值训练时会出现计算困难问题。国内外许多研究者采用被控对象的模型辨识方法来解决此问题，但是，计算量也大，实时性差，而且对于时变系统，模型辨识不能实现。

若算法是收敛的，则必有|E(k+1)|＜|E(k)|，且|e(k)|＜|E(k)|，故只要满足|E(k+1)|＜|e(k)|即可保证算法收敛的。据此，设 E ( k + 1 )=αe(k)，且0＜α＜1。由于α可通过学习率μ来弥补，因此，可将α隐含在学习率μ中。

此外，用符号函数来替代 ∂ y(k +1)/∂u(k)也是可行的。因为其符号的正负只决定权值变化的方向，其数值只影响权值的变化速度，而权值变化速度也可通过学习率μ弥补。设

则式(17)～(19)可改写为：

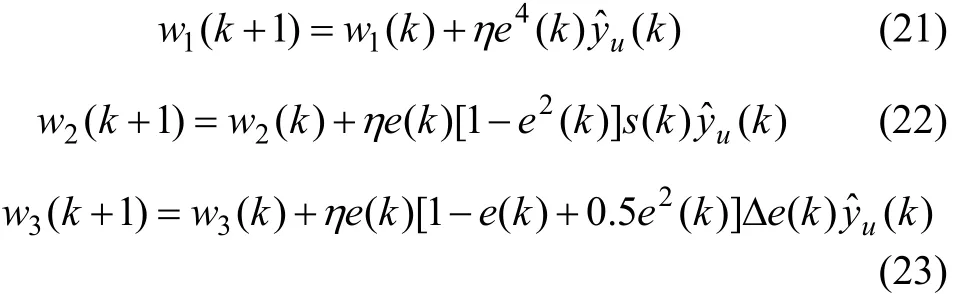
α已隐含在学习率η中。为了有效避免因权值过大引起神经网络训练过程中出现振荡现象，通常对权值进行归一化处理，即

由式(21)～(23)可知，权值的计算只与当前或历史的系统输入(r(k)和r(k-1))、输出(y(k)和y(k-1))以及历史控制信号(u(k-1)和u(k-2))有关，因而有效解决了权值计算问题。由于本文研究的非线性PID神经网络控制器只涉及乘法和加法运算，便于CPU处理，因此，计算简单，计算量小，便于实际应用。

2.4 算法收敛性

为了保证系统稳定工作，必须对算法的收敛性进行理论研究，以便为确定学习率提供理论依据，避免选择学习率的盲目性。

将E(k +1)=αe(k)和式(26)代入式(25)，并整理可得：

由式(27)知：要使神经网络算法收敛，必须有下式成立：

2.5 算法步骤

(1) 神经网络权值初始化：wj=0(j=1, 2, 3)，设s(-1)=0，e(-1)=0，u(m)=0，y(m)=0(m=-1, -2, …)；

(2) 计算系统初始误差：E(k)=r(k)-y(k)，由式(8)计算归一化误差e(k)；

(3) 分别计算累积误差和差分：s(k)=s(k-1)+e(k)，Δe(k)=e(k)-e(k-1)；

(4) 由式(20)计算符号差商)(ˆkyu，并计算学习率

(5) 由式(21)～(23)递推计算神经网络权值系数w1，w2和w3，由式(24)对权值进行归一化处理；

(6) 由式(7)计算非线性PID控制器的控制率u(k)，即

(7) 返回步骤(2)重复上述计算过程，以实现非线性 PID神经网络智能控制器的在线实时优化控制过程。

3 仿真结果

为了验证动态非线性PID神经网络智能控制器的有效性，选择文献[15]中的对象A和B进行仿真实例研究。

例1 对象A是1个一阶惯性大、纯滞后工艺对象，且1/＞＞Tτ，其传递函数为[15]

由文献[15]可知：若利用常规控制算法控制该对象，则很难获得满意的控制效果。在本文算法中，使权值的初始值为0，给定学习率η=2×10-3，采样周期为0.1 s，通过神经网络实时在线训练，其仿真结果如图3(a)所示，文献[15]中的仿真结果如图3(b)所示。

图3 实例1仿真结果Fig.3 Simulation results of example 1

由图 3可知：采用本文方法，调节时间约为400 s，而采用NOIC方法[15]则需要650 s。由图3(b)还可知：使用传统PID控制方法无法对该对象实现有效控制。

例2 对象B是1个非线性对象，其离散化方程为[15]：

其中：u(k)和y(k)分别是被控对象的输入和输出变量。在本文算法中，使权值的初始值为 0，给定学习率为η=2×10-4，设采样周期为0.1 s，通过神经网络在线训练，其仿真结果如图 4(a)和4(b)所示，且超调量为1.33×10-13%，稳态误差为0，调节时间为5 s。而文献[15]中的仿真结果如图 4(c)所示，超调量为 15%，稳态误差为0，调节时间为10 s。

图4 实例2仿真结果Fig.4 Simulation results of example 2

4 结论

(1) 通过分析常规PID参数随系统过渡过程误差变化的理想变化关系，分别给出了比例、积分和微分增益参数关于误差信号的二次非线性函数，不仅大大简化了3个增益参数的非线性函数模型，而且通过神经网络在线训练使3个增益参数的非线性函数模型分别随权值w1，w2和w3实时动态变化，从而获得将动态非线性PID控制与神经网络控制融为一体的智能控制模型。

(2) 计算机仿真结果验证了本文基于神经网络算法的非线性PID控制器的有效性。与传统PID控制器相比，采用本文方法不仅计算量大大减小，便于实际应用，而且超调小，调节时间短。

[1] HAN Jin-qin. Nonlinear PID controller[J]. Acta Automatica Sinica, 1994, 20(4): 487-490.

[2] CHENG Zhong, YAN Wei, LI Zu-shu, et al. HSIC-based nonlinear PID controller[J]. Control and Decision, 2003, 18(6):694-697.

[3] XU Ying, Hollerbach J M, Ma D. A nonlinear PD controller for force and contact transient control[J]. IEEE Control Systems Magazine, 1995, 15(1): 15-21.

[4] Shahruz S M, Schwartz A L. Nonlinear PI Compensators that achieve high performance[J]. Journal of Dynamic Systems Measurement and Control, 1997, 119: 105-110.

[5] HU Bao-gang, Mann G KI, Gosine R G. Control curve design for nonlinear (or fuzzy) proportional actions using spline-based functions[J]. Automatica, 1998, 34(9): 1125-1133.

[6] Bucklaew T P, LIU Chun-sha S. A new nonlinear gain structure for PD-type controllers in robotic applications[J]. Journal of Robotic Systems, 1999, 16(11): 627-649.

[7] Armstrong B, Neevel D, Kusik T. New results in NPID control:Tracking, integral control, friction compensation and experimental results[J]. IEEE Transactions on Control Systems Technology, 2001, 9(2): 399-406.

[8] GAO Zhen. From linear to nonlinear control means: a practical progression[J]. ISA Transactions, 2002, 41(2): 177-189.

[9] 胡包钢. 非线性 PID控制器研究: 例分量的非线性方法[J].自动化学报, 2006, 32(2): 219-227.HU Bao-gang. A study on nonlinear PID controllers:Proportional component approach[J]. Acta Automatica Sinica,2006, 32(2): 219-227.

[10] HU Bao-gang, YING Hao. Review of fuzzy PID control techniques and some important issues[J]. Acta Automatica Sinica,2001, 27(4): 567-584.

[11] Ruano A E B, Fleming P J, Jones D I. Connectionist approach to PID autotuning[J]. IEE Proceedings D: Control Theory and Applications, 1992, D139(3): 279-285.

[12] 韩华, 罗安, 杨勇. 一种基于遗传算法的非线性PID控制器[J].控制与决策, 2005, 20(4): 448-454.HAN Hua, LUO An, YANG Yong. A nonlinear PID controller based on genetic tuning algorithm[J]. Control and Decision,2005, 20(4): 448-454.

[13] 郭彦青, 姚竹亭, 王楠. 非线性PID控制器研究[J]. 中北大学学报: 自然科学版, 2006, 27(5): 423-425.GUO Yan-qing, YAO Zhu-ting, WANG Nan. The study on non-linear PID controller[J]. Journal of North University of China: Natural Science Edition, 2006, 27(5): 423-425.

[14] 刘金琨. 先进PID控制及其MATLAB仿真[M]. 北京: 电子工业出版社, 2003: 20-80.LIU Jin-kun. Advanced PID control and MATLAB simulation[M]. Beijing: Electronic Industry Press, 2003: 20-80.

[15] 刘宝, 丁永生, 王君红. 基于NEI调节机理的非线性智能优化控制器[J]. 控制与决策, 2008, 23(10): 1159-1162.LIU Bao, DING Yong-sheng, WANG Jun-hong. Nonlinear optimized intelligent controller based on modulation of NEI system[J]. Control and Decision, 2008, 23(10): 1159-1162.