基于ARMA-TS-GARCH有限混合模型的交通数据分析

王维强，牛振东，曹玉娟，赵育民，赵堃

(北京理工大学 计算机学院，北京，100081)

ARMA模型和APARCH模型分别是统计时间序列模型和结构计量经济模型。过去30年中，这2种模型被计量经济学家用于预测。目前，非线性ARCH族模型特别是GARCH(1，1)模型因为可以用于解释大量的经济数据和活动而逐渐用于各个领域。自从 Engle提出ARCH模型后, GARCH成为处理时间序列数据非常重要的模型，特别是在处理金融数据中，用于分析和预测数据的波动性[1]。GARCH模型其方差随着时间的变化而变化，并且具有波动性和纵集性。目前，将GARCH族模型用于交通量的预测和研究甚少，因此，研究时间序列模型对交通数据的拟合和预测具有重要意义。为此，本文作者选用美国加州洛杉矶长滩地区交通量为研究对象，提出新的时间序列模型对其进行拟合、分析和预测，以便为控制交通量的增长和进一步控制废气排放提供理论依据。

1 模型及提出模型

1.1 GARCH模型

ARMA(Generalized ARCH)模型用于时间序列中主要是建立序列的自回归方程，而 GARCH模型则主要用于研究序列的方差。在广义自回归条件异方差模型(Generalized autoregressive conditional heteroscedasticity model，简记为GARCH模型)中，要考虑2个不同的设定：一个是条件均值，另一个是条件方差[2-3]。在标准化的GARCH(1,1)模型中，

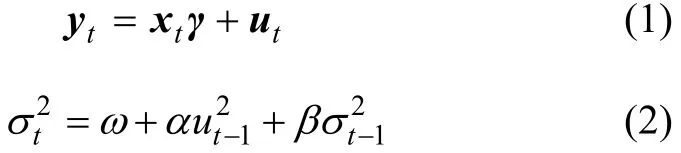
其中：xt为 1×(k+1)维外生变量向量；γ为(k+1)×1维系数向量。式(1)中给出的均值方程是一个带有扰动项的外生变量函数。由于是以前面信息为基础的一期向前预测方差，所以，它被称作条件方差，式(2)也被称作条件方差方程。

近年来，出现了一大批GARCH模型的变形，其中，除 ARCH和 GARCH模型之外，还有不对称幂ARCH模型即APARCH模型，包括特殊的TS-GARCH模型、GJR-GARCH模型、T-ARCH模型、N-ARCH模型、Log-ARCH模型等[4-9]。

APARCH(p,q) 的方差方程可以描述成如下形式：

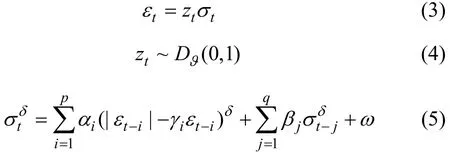
式中：iγ为杠杆影响参数；δ为Taylor影响参数；q为持久性因子；zt是1个均值为0、方差为独立分布的随机过程参数； (0,1)Dϑ是以0为均值、方差为1的概率密度函数；ϑ是分布参数，用来描述函数分布的形状和峰度。

此模型增加了1个不对称参数通过指数变化的灵活性来解释函数的杠杆作用。

若所有的系数 β=0，则 GARCH 模型就降维成ARCH模型。

1.2 ARMA-TS-GARCH模型的构造

ARMA-TS-GARCH模型类似于 AR-GARCH模型，分开来看，每一个混合模型的成分都可以定义成普通的ARMA模型：式(6)也可以写成：

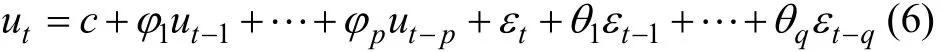
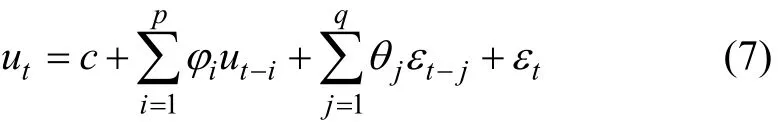
ARMA模型常常也被称为混合模型，记作ARMA(p,q)。当p=0 时，ARMA(0, q)=MA(q)；当q=0时，ARMA(p, 0)=AR(p)。

另外，每一个残差项,tjε都代表高斯分布变量的白噪音(White noise)，并且GARCH模型可以表示成如下形式：

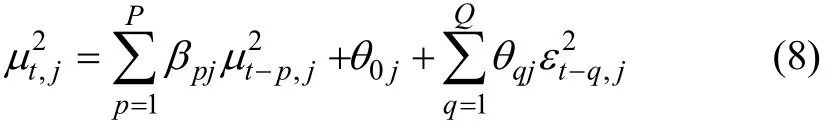
其中：qjθ＞0；q=1, …, Q。并且当pjβ＞0时，p=1, …,P。根据定义，当δ=1和γi=0时，TS-GARCH模型表示如下：

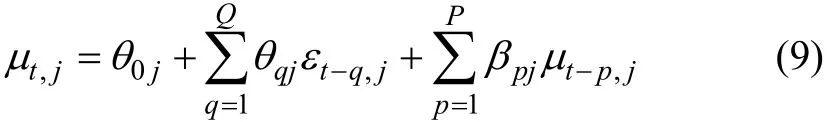
因此，可以在数学上用K-成分高斯混合模型得到有限混合ARMA-TS-GARCH模型，它的表现形式如下：

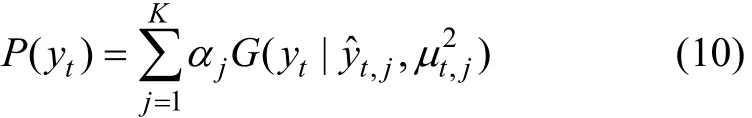
其中：

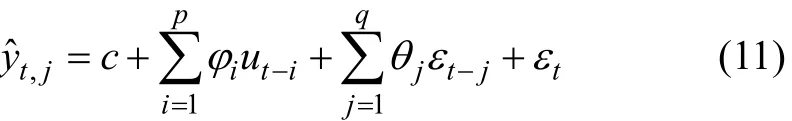
并且jα

从式(9)～(11)可得新模型ARMA-TS-GARCH的表示形式。

2 数据描述

交通量的数据来自加州交通局属的交通和车辆数据系统分局。每月给出车辆里程数的报告。该报告由交通数据科制作，对驾驶者在美国加利福尼亚州公路上行驶的车辆里程数进行估计。该估计的方法是：1个样本有22个流量监测点，其中包括各种巷道类型来用来计算车辆的行驶里程。

对美国洛杉矶长滩地区的所有数据集的数据从2000年1月到2006年12月进行总体统计，相应的时间序列图如图1所示。

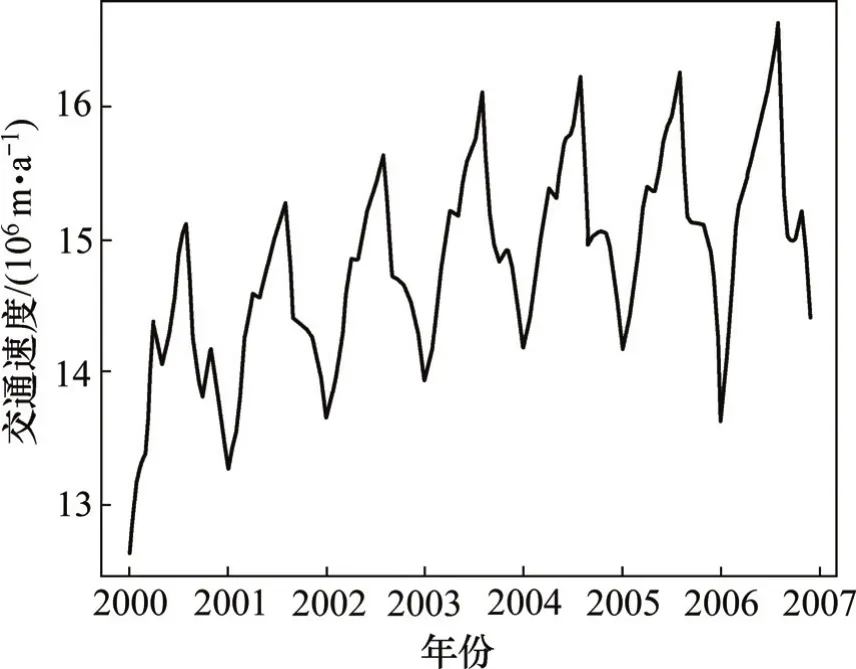
图1 洛杉矶长滩2000—2006年交通量时序图Fig.1 LA long beach Traffic series plot in 2000—2006

3 参数估计与诊断检验

3.1 参数估计

从图1可以看出：交通量逐年上涨。这与买车的数量逐年上涨相符。此外，车流量也是以年为周期呈季节性变化。

ARMA(p,q)模型中AR和MA参数部分应使用关键词ar和ma定义。而TS-GARCH(p,q)中的参数部分在这里用关键词α和β定义。模型参数值估计结果如表1所示。从表1可见：参数都小于1。取参数值为1，这样，此模型为ARMA(1,1)-TS-GARCH(1,1)。

表1 模型参数估计Table 1 Model parameter estimation

3.2 模型的检验

在GARCH模型的框架内对异方差时间序列的参数进行估计。但是，参数估计不是对 ARMA-TSGARCH模型进行分析的唯一方面，还包括：时间序列模型的定义，时间序列模型仿真的检验，参数估计，诊断分析，对预测的计算等。

对于含有ARMA项的模型，基于残差的回归统计量，如R2和DW都是以一期向前预测误差为基础计算的。1个含有AR项的模型有2种残差：第1种是无条件残差，第2种是估计的一期向前预测误差。这种残差代表预测误差。实际上，通过利用滞后残差的预测能力，提高了无条件预测能力，隐藏低了残差。

下面对 ARMA-TS-GARCH模型进行诊断和检验。

(1) 残差检验。残差检验包括对估计方程残差的序列相关、正态性、异方差性和自回归条件异方差性进行检验[10-13]。

对1个序列分布的最简单非参数密度估计是采用直方图。直方图对原点的选择比较敏感并且是不连续的。非参数密度估计直方图检验结果见图 2。从图 2可以看出：数据集的直方图的中心与0稍有偏离，但比较接近。

图2 直方图检验Fig.2 Histogram test

Quantile-Quantile( Q-Q图)检验对于比较2个分布是一种简单而又有效的重要工具，可反映一个被选序列的分位数分布相对于另一个序列的分位数分布或一个理论分布的异同，或者模型与数据之间的拟合程度。图3所示为非参数密度估计Q-Q图。其中，直线的斜率为标准差，截距为均值。从图3可以看出：数据基本围绕在线的周围上下波动，基本没有很大的离群点，说明模型对数据拟合程度良好。

残差是实际值与回归预测值之间的差[14-15]。残差图以残差为纵坐标，以任何其他指定的量为横坐标的散点图，可用于检查回归线的异常点。若描绘的点围绕残差等于0的直线上下随机散布，则说明回归直线对原观测值的拟合情况良好，说明变量X与y之间有显著的线性相关关系；否则，说明回归直线对原观测值的拟合不理想。非参数密度估计残差检验结结果见图4。从图4可见：数值点都是在[-1, 1]的区间内，围绕0上下波动，虽然偶有几个离群值，但是都没有超出绝对值为1的区间，可见：回归预测值与实际值的拟合较理想。

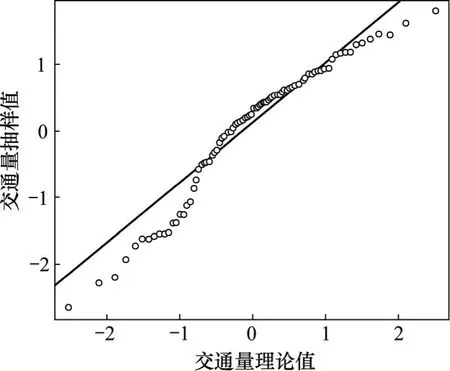
图3 Q-Q图检验Fig.3 Q-Q Plot test

图4 残差检验Fig.4 Residual test

4 与其他模型的比较

为了进一步证明ARMA-TS-GARCH模型的优越性，将其与经典模型GARCH和ARMA-GARCH进行比较。用它们对同样的数据集进行分析，比较的信息准则是 AIC, BIC, SIC和HQ。所得结果见表2。AIC,BIC, SIC和HQ这4个信息准则的值越小，证明这个模型越好。从表2可以看出ARMA-TS- GARCH模型的各种信息标准结果都比 ARMA- GARCH模型和GARCH模型的低[17]，这说明ARMA- TS-GARCH模型在处理某些时间序列数据(如交通量数据集)时，比其他模型更具有优越性和准确性。

表2 模型的信息标准统计比较Table 2 Model Information Criterion statistical comparison

5 模型的预测

对异方差时间序列进行预测，可以得出对数据的条件均值和对条件方差进行预测的公式。

一个平稳序列的数字特征如均值、方差和协方差等不随时间的变化而变化，时间序列在各个时间点上的随机性服从一定的概率分布[16-17]。也就是说，对于一个平稳的时间序列，可以通过过去时间点上的信息，建立模型拟合过去信息，进而预测未来的信息。

这里采用ARMA-TS-GARCH模型进行预测，所得结果见表3。可见：采用 ARMA-TS-GARCH模型进行预测，总共获得10期预测值，所得的预测均值在达到一个高点之后趋于平稳，而标准方差则一直处于平稳状态。

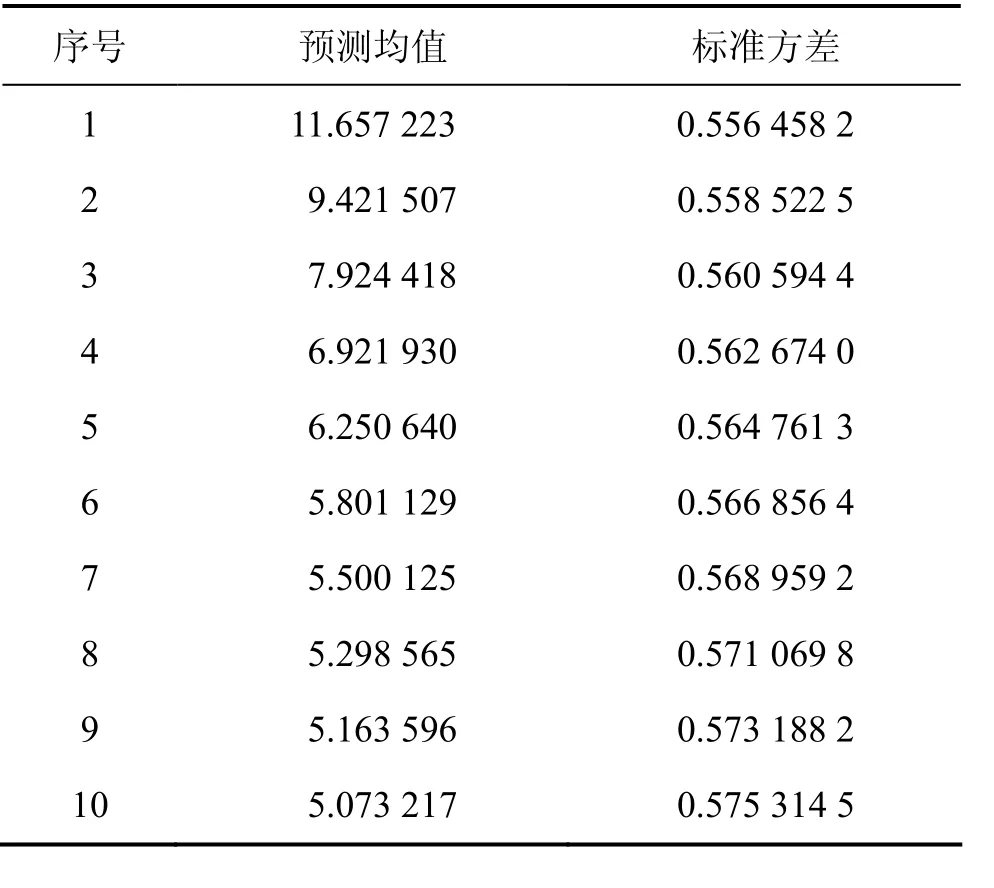
表3 ARMA-TS-GARCH的预测值Table 3 Prediction results of ARMA-TS-GARCH

6 结论

(1) 通过对ARCH模型、GARCH模型以及ARCH模型的多种变形模型进行分析，在基于K成分高斯模型的基础上提出了ARMA-TS-GARCH模型。

(2) 采用 ARMA-TS-GARCH 模型对洛杉矶长滩地区 2000—2006年交通量进行建模和拟合，得到ARMA(1,1)-TS-GARCH(1,1)模型，并且对其进行多种检验诊断分析，然后将其分析结果与经典模型GARCH和 ARMA-GARCH进行比较，结果表明ARCH-TS-GARCH模型在处理某些事件序列数据如周期性的环境数据时具有较强的优越性。

[1] Lanne M, Saikkonen P. A multivariate generalized orthogonal factor GARCH model[J]. Journal of Business and Economic Statistics, 2007, 25(1): 61-75.

[2] Moon Y S, Whang K Y, Loh W K. Duality-based subsequence matching in time series databases[C]//Proceeding 98 of 17th International Conference on Data Engineering. San Jose, USA,2001: 263-272.

[3] He C, Terasvirta T. An extended constant conditional correlation GARCH model and its fourth-moment structure[J]. Econometric Theory, 2004, 20(1): 904-926.

[4] Engle R F, GARCH 101: An introduction to the use of ARCH/GARCH models in applied econometrics forthcoming[J].Journal of Economic Perspectives, 2001, 12(2): 17-32.

[5] Wang T S F, Wens M H. Efficient subsequence matching for sequences databases under time warping[C]//Proceedings of 7th International Database Engineering and Applications Symposium. Hong Kong, 2003: 132-141.

[6] Brooks C, Burke S P, Persand G. Benchmarks and the accuracy of GARCH model estimation[J]. International Journal of Forecasting, 2001, 17(1): 45-56.

[7] Bernhard Pfaff. Analysis of integrated and cointegrated time series with R[J]. Springer, 2005, 12(3): 21-79.

[8] Keogh E, Pazzani M. Scaling up dynamic time warping for data mining application[C]//Proceeding of the Sixth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Boston, 2000: 256-289.

[9] Keogh E, Smyth P. A probabilistic approach to fast pattern matching in time series database[C]//Proceeding of 3th International Conference of Knowledge Discovery and Data Mining. Newportbeach: AAAI Press, 1997: 20-24.

[10] Keogh E, Pazzani M. An indexing scheme for fast similarity search in large time series database[C]//Scientific and Statistical Database Management, Elventh International Conference. Ohio,1999: 56-57.

[11] Keogh E, Chakrabarti K, Mehrotra S, et al. Locally adaptiye dimensionality reduction for indexing large time series database[C]//ACM SIGMOD 2001. Santa Barbara, California,2001: 78-99.

[12] Cadez I V, Heckerman D, Meek C, et al. Vi-sualization of navigation patterns on a web site using model-based clustering[C]//Knowledge Discovery and Data Mining. Boston,2000: 280-284.

[13] Baillie R T, Chung C F, Ticslau M A. Analyzing industrialized countries inflation by the fractionally integrated ARFIMA—GARCH model[J]. Journal of Applied Econometrics,1996, 3(11): 23-40.

[14] Hauser M A, Kunst R M. Forecasting high frequency financial data with the ARFIMA-ARCH model[J]. Journal of Forecasting,2001, 20(7): 501-518.

[15] Rastogi R, Shim K PUBLIC. A decision tree classifier that integrates building mad pruning[C]//Proceedings of the 24th International Conference OU very Large Databases (VLDB’98).New York, 1998: 405-415.

[16] Keerthi S S. Convergence of a generalized SMO algorithm fur SVM classifier design TRCD[C]//Control Division Dept of Mecha and Prod Engineering National University of Singapore.Singapore, 2000: 13-27.

[17] Loh W K, Kim S K. A subsequence matching algorithm supporting moving average transform of arbitrary order in time-series databases using index interpolation[C]//Proceedings 12th Australasian Database Conference. Queensland, 2001:37-44.