基于非结构化网格的三维大地电磁自适应矢量有限元模拟

刘长生 ，汤井田，任政勇 ，冯德山

(1. 中南大学 信息物理工程学院，湖南 长沙，410083；2. 长沙航空职业技术学院 计算机系，湖南 长沙，410014；3. 瑞士联邦理工学院(EIH) 地球物理系，瑞士 苏黎士，CH8092)

自 Coggon[1]提出地球物理电磁中的有限单元算法(Finite element method, FEM)以来，FEM开始在电磁勘探领域得到广泛应用[2-5]。Badea等[6]利用节点型的线性有限单元模拟了可控源音频大地电磁法；Mitsuhata等[7]基于电场标量势和磁场矢量势的 T-Ω公式，利用线性的向量有限单元计算了三维大地电磁模型；Nelson等[8-10]利用非结构化网格来解决网格剖分的几何离散化误差问题，从而计算了三维电磁矢量有限元模拟；阮百尧等[11]利用节点型有限单元实现了三维地电断面的正演等；王烨等[12]采用基于棱边的矢量有限元方法计算了三维大地电磁模型。目前，地球物理电磁FEM计算存在1个问题：数值计算结果的精度完全取决于初始模型的离散化网格。对于简单的电磁模型，基于经验可以得到较优化的离散网格；而对于复杂 3D地电模型，电磁场的形态和变化趋势复杂，仅凭人为经验难以得到优化网格。为了提高复杂区域的电磁场精度，网格可以进行加密(h型自适应[13-14])，另外也可以提供局部拟合电磁场的形状多项式函数的阶次p(p型自适应[15-16])。相对于p型自适应策略，h型自适应策略更容易嵌入现有的代码之中，从而缩短动运算时间。Key等[17]利用h型自适应网格的思想对二维大地电磁模型的模拟进行了研究；Li等[18]将这一概念引入到二维可控源电磁法之中。对于三维模拟，本文作者利用非结构化网格，提出基于后验误差的h型自适应加密的3D大地电磁模拟算法。

1 三维MT矢量有限元数学模型

三维 MT 模型的一般地电结构如图 1所示，其中：0σ，1σ和2σ分别为空气层、地下地层和地下埋藏的异常体的电导率。

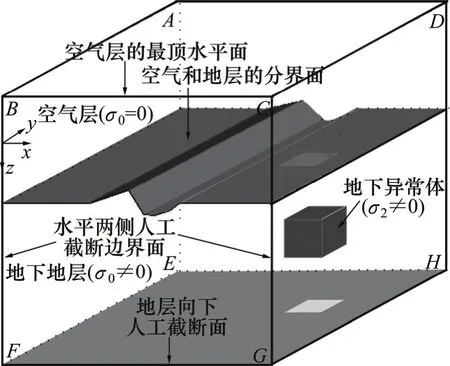
图1 三维MT模型的一般地电结构Fig.1 MT model of three-dimensional structure of general earth electricity

在空气层和地下地层区域，电场满足下面微分控制方程[19]：

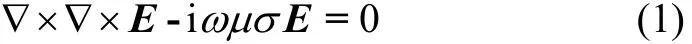
式中：E为电场强度；i为虚数；ω为角频率；μ为自由空间磁导率；σ为MT模型的电导率。

采用理论可靠和执行简单的Direlet边界条件[20]，并采用水平地层地电结构在边界上的电磁场近似作为边界条件。

式中：n为外边界的外单位法向量；E0为外边界上给定的已知电场强度。

方程(1)和(2)定义了MT问题的边值问题。借助于矢 量 恒 等 式Gauss分部积分公式，其对应的变分公式为：

式中：H(curl)为 Hilbert空间向量， H (curl)=；Ω 为求解区域；L2(Ω)为平方可视的Hilbert空间；b为双线性表达式；f为单线性表达式。

此处采用矢量有限元法求解方程(3)所表示的电场分布。为此，需要把整个求解区域离散成一系列四面体单元。它与节点型有限元不同之处在于：四面体单元中电场强度E由每条边的切向方向定义。考虑任意的四面体单元 e，并把该单元中电场的近似表达式表示为：

为了避免伪数值解，节点型有限元法必须加入额外的罚项，进而加大了理论难度。而矢量有限元法由于其矢量形状函数的散度为0，电流密度的无散度要求自然得到满足；并考虑到矢量形状函数仅仅沿四面体边的切向连续，因此，电场的切向连续性条件得到满足，法向不连续性条件被保留，故基于矢量形状函数的四面体单元能有效地避免出现伪解。

MT 模型求解的大型复线性方程为：

其中：U为定义在各个四面体单元的边上电场切向未知数向量。矩阵A和B由各个单元的贡献所得[21]：

式中：Bi仅仅在位于外Dirichlet边界面上的边不为0。

2 基于残差的后验误差估计

采用Nédélec四面体线性单元，其求解过程可以表述为：定义Tk为计算区域Ω的一系列四面体网格剖分单元，Fk为网格中的一系列三角面；定义Tk上的有限元空间Uk为[21]：

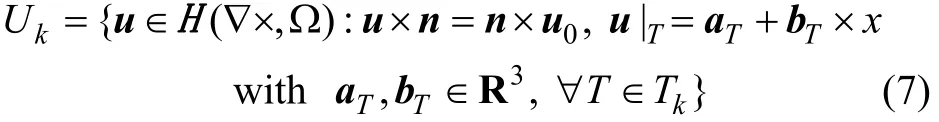
在Tk上，有限元计算可表示为：求解Ek∈Uk，使其满足

式中：)(2ΩL∈f；)(2ΩL∂∈g。

定义数值解的误差为：

经推导，适合于MT模型的后验误差估计为：

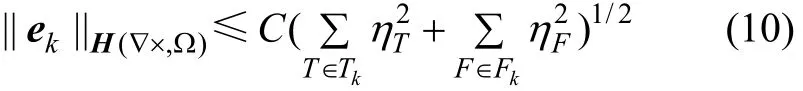
式中：C为一依赖于问题的常数；ηT和ηF分别为四面体单元和三角面的局部误差。

3 自适应策略

采用h型自适应有限元对MT模型进行数值模拟，网格剖分采用约束的 Delaunay四面体(DT)非结构化方法及相应的加密算法。对于任意模型，只要给出初始网格和全局误差控制值，利用h型自适应迭代策略，计算机即可全自动求解，无需人工干预。

在四面体网格Tk上，利用有限元方法求出Ek，根据文献[22]中的误差收敛理论，得出当前网格上的误差估计，并得到单元上的局部误差估计指示值：

相应地，全局误差指示值和最大误差估计指示值分别为：

当计算单元误差超过给定的误差限后，采用相应的加密策略，具体算法流程如图2所示。

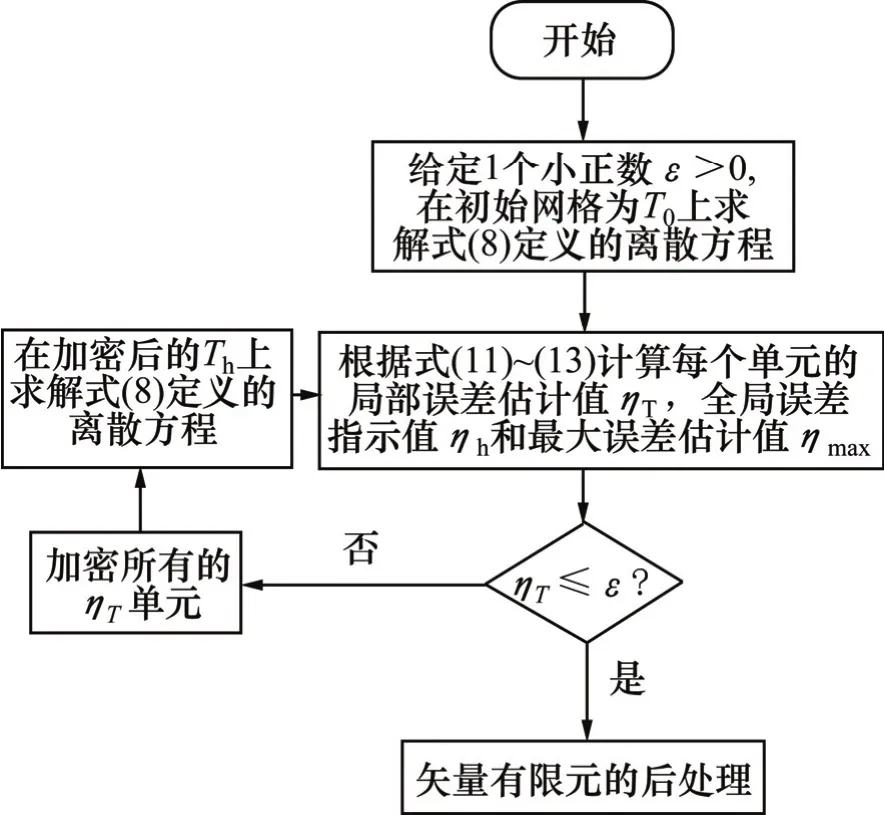
图2 具体算法流程图Fig.2 Flow chart of calculation method

算法中影响自适应加密过程的终止因子为1个给定小正数ε和加密密度因子β。通常来说，ε小于1，而β的最佳值为0.5～0.7。对于不同的问题，正数ε也相差较大，ε[1∈×10-10, 0.1]。另外，在实际计算过程中，还引入最大迭代次数n和最大内存消耗M来控制自适应终止，一般取n=10，M=500 MB。

4 COMMEMI 3D-1 MT模型数值模拟算例

为了加强对比分析，选取国际通用的标准测试模型COMMEMI 3D-1 model进行模拟[23]。其中：六面体异常体的电阻率为 0.5 Ω·m，围岩的背景电阻率为100 Ω·m，其对比度达1∶200。求解的空间维数如下：x方向长度为100 km，y方向长度为100 km，z方向上空气层厚度为50 km，大地层厚度为50 km。MT测线分布在x和y坐标轴上，长度范围均为0～3 km。测点个数为121，工作频率为f=0.1 Hz。

自适应控制参数为：ε=0.01，β=0.7，n=25，M=500 MB。实际迭代步数为20步，内存最大为128.5 MB。初始网格为 10 553个节点，65 896个单元和153 060条边；自适应加密的第12步网格规模为13 238个节点，79 658个单元和186 854条边；最后一步的网格为19 538个节点，113 281个单元和267 798条边。为了计算方便，测试平台选用DELL D620笔记本电脑进行数值模拟，计算频点分别是32，16，8，4，2，1，0.5，0.25和0.1 Hz，总耗时为317.461 4 s。其中：初次网格是采用tetgen软件进行剖分，自动加密采取二分加密，时间均少于 1 s。自动频点计算最大耗时56.811 0 s，最小耗时23.319 5 s，平均耗时35.273 5 s。

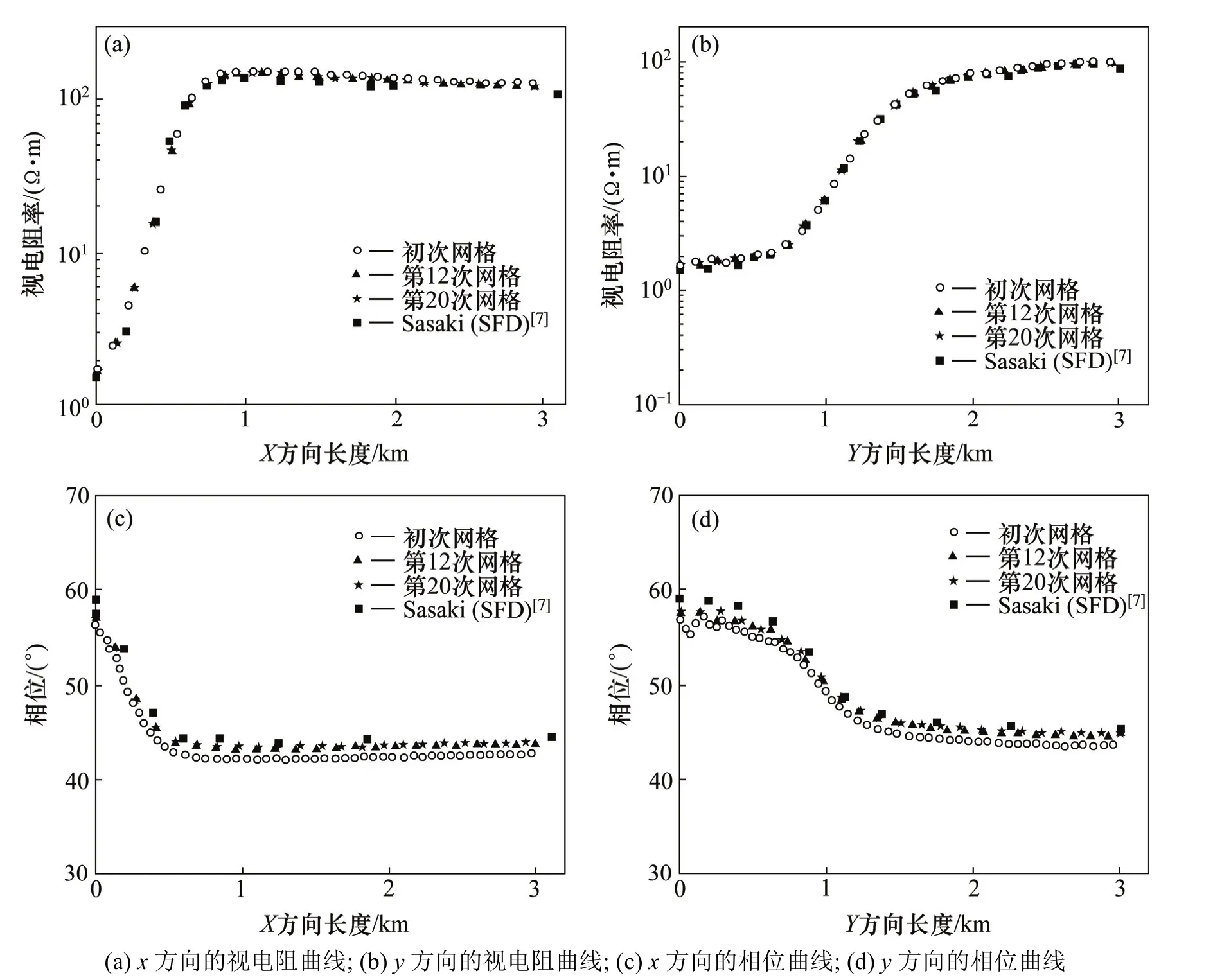
图3 频率为0.1 Hz、含不均匀立方体MT模型的地表测点上的相位和视电阻率曲线Fig.3 Phase and resistivity curves containing uneven surface cube measuring point when frequency is 0.1 Hz

通过模拟得到 3D-1模型的自适应加密网格的后验误差分布。以0.1 Hz频点模拟情况进行分析：在初始网格上的单元误差较大，平均误差为74.48%，最大误差为 165.00%。因此，较大的误差分布驱使设计的自适应加密策略运作，并加密误差大的单元。这一结果在第12和20次网格上可以明显看出。在第12次网格上，单元平均误差减至3.33%，最大误差减至6.12%；在第 20次网格上，单元平均误差减至 0.93%,最大误差减至3.98%，其平均误差小于给点的1%，因此，加密过程终止。数值模拟结果与Sasaki针对本模型所得计算结果较吻合(见图3中的Sasaki(SFD))[7]。

注意到测线附近的单元并没有随着自适应加密过程的运行而对网格显著加密。这一现象导致测线附近数值精度提高(见图3)：视电阻率的平均误差从初始网格上的3.49%减低为第12次网格上的0.87%，但是，随着网格的再加密，视电阻率平均误差始终保持在0.50%～1.00%；相位曲线的平均误差从初始网格上的1.23%减低为第20次时的0.21%。但是，随着网格的再加密，相位曲线平均误差始终保持在0.20%～0.50%。

5 结论

(1) 根据电场微分控制方程和边界条件，采用基于矢量形状函数的四面体单元，其矢量形状函数的散度为0，电流密度的无散度要求就被自然满足，因此，能有效地避免伪解的出现，从而建立了三维MT矢量有限元数学模型。

(2) 推导出基于残差的三维大地电磁矢量有限元后验误差估计公式，为三维大地电磁自适应矢量有限元数值模拟的实现奠定了基础。

(3) 在完全非结构化四面体单元剖分及优化基础上，结合三维大地电磁矢量有限元后验误差估计公式，提出了基于非结构化网格的三维大地电磁h型自适应矢量有限元计算策略，保证了对复杂大地电磁模型数值计算的精度和可靠性。

(4) 电磁模型的复杂性总体上不影响方法的收敛性，且可以达到预期的计算精度。可见，h型自适应矢量有限元可以保证复杂模型的计算精度和速度，具有广阔的应用前景。

[1] Coggon J H. Electromagnetic and electrical modeling by the finite element method[J]. Geophysics, 1971, 36(1): 132-145.

[2] Pridmore D F, Hohmanns G W, Ward S H, et al. An investigation of finite-element modeling of electric and electromagnetic data in three dimensions[J]. Geophysics, 1981, 46(7): 1009-1024.

[3] 李大潜. 有限元素法在电法测井中的应用[M]. 北京: 石油工业出版社, 1980: 15-67.LI Da-qian. The application of finite element method in electric well logging[M]. Beijing: Petroleum Industry Press, 1980:15-67.

[4] 罗延钟, 张桂青. 电子计算机在电法勘探中的应用[M]. 武汉:武汉地质学院出版社, 1987: 51-99.LUO Yan-zhong, ZHANG Gui-qing. Application of electronic computer in electrical prospecting[M]. Wuhan: Press of Wuhan College of Geology, 1987: 51-99.

[5] 徐世浙. 地球物理中的有限单元法[M]. 北京: 科学出版社,1994: 23-28.XU Shi-zhe. Finite element method in geophysics[M]. Beijing:Science Press, 1994: 23-28.

[6] Badea E A, Everett M E, Newman G A, et al. Finite-element analysis of controlled-source electromagnetic induction using Coulomb-gauged potentials[J]. Geophysics, 2001, 66(3):786-799.

[7] Mitsuhata Y, Uchida T. 3D magnetotelluric modeling using the T-Ω finite-element method[J]. Geophysics, 2004, 69(1):108-119.

[8] Nelson E M. Advances in 3D Electromagnetic finite element modeling[C]//Proceedings of the IEEE 1997 Particle Accelerator Conference. Vancouver, Canada, 1998: 1837-1840.

[9] Sugeng F. Modeling the 3D TDEM response using the 3D full-domain finite-element method based on the hexahedral edge-element technique[J]. Exploration Geophysics, 1998, 29(4):615-619.

[10] Yoshimura R, Oshiman N. Edge-based finite element approach to the simulation of geoelectromagnetic induction in a 3-D sphere[J]. Geophysical Research Letters, 2002, 29(3):1039-1045.

[11] 阮百尧, 熊彬, 徐世浙. 三维地电断面电阻率测深有限元数值模拟[J]. 地球科学, 2001, 26(1): 73-77.RUAN Bai-yao, XIONG Bin, XU Shi-zhe. Finite element method of modeling resistivity sounding on 3D geoelectic section[J]. Earth Science, 2001, 26(1): 73-77.

[12] 王烨. 基于矢量有限元的高频大地电磁法三维数值模拟[D].长沙: 中南大学信息物理工程学院, 2008: 35-62.WANG Ye. A study of 3D high frequency magnetotellurics modeling by edge-based finite element method[D]. Changsha:Central South University. School of Info-physics and Geometrics Engineering, 2008: 35-62.

[13] Zienkiewicz O C, Zhu J Z. Adaptive and mesh generation[J]. Int J Num Meth Eng, 1991, 32(4): 783-810.

[14] Tani K, Yamada T. H-version adaptive finite element method using edge element for 3D non-linear magnetostatic problems[J].IEEE Transactions on Magnetics, 1997, 33(2): 1756-1759.

[15] Szabo B A. Mesh design for the p-version of the finite element method[J]. Computer Methods in Applied Mechanics and Engineering, 1986, 55(1): 181-197.

[16] WEN Dai-gang, JIANG Ke-xun. P-version adaptive computation of FEM[J]. IEEE Transactions on Magnetics, 1994, 30(5):3515-3518.

[17] Key K, Weiss C. Adaptive finite-element modeling using unstructured grids: The 2D magnetotelluric example[J].Geophysics, 2006, 71(6): 291-299.

[18] LI Y G, Key K, Constable S. An adaptive finite element modeling of 2-D marine controlled-source electromagnetic fields[C]//18th IAGAWG 1.2 Workshop on Electromagnetic Induction in the Earth. El Vendrell, Spain, 2006: S3-S14.

[19] Harrington R F. Time harmonic electromagnetic fields[R]. New York: McGraw-Hill Book Co, 1961: 37-85.

[20] Nam M J, Kim H J, Song Y, et al. 3D magnetotelluric modeling including surface topography[J]. Geophysical Prospecting, 2007,55(2): 277-287.

[21] LIU Chang-sheng, REN Zheng-yong, TANG Jing-tian, et al.Three-dimensional magnetotellurics modeling using edge-based finite element unstructured meshes[J]. Applied Geophysics, 2008,5(3): 170-180.

[22] CHEN Zhi-ming, WANG Long, ZHENG Wei-ying. An adaptive multilevel method for time-harmonic Maxwell equations with singualarities[J]. Siam J Sci Comput, 2007, 29(1): 118-138.

[23] Zhdanov M S, Varentsov I M, Weaver J T, et al. Methods for modeling electromagnetic fields Results from COMMEMI—the international project on the comparison of modeling methods for electromagnetic induction[J]. Journal of Applied Geophysics,1997, 37(3/4): 265-271.