一种发现交叠社团的快速层次化算法

彭佳扬，杨路明，王建新，李敏，蔡娟

(中南大学 信息科学与工程学院，湖南 长沙，410083)

在现实世界中，很多自然、社会和科学系统都以网络的形式存在，这些网络很复杂，被称为“复杂网络”[1]。随着人们对复杂网络的拓扑结构、物理意义和数学特性的深入研究，发现许多实际网络不但具有小世界性、无标度性等基本统计特性，还具有拓扑结构属性——社团结构，具有同社团节点相互连接紧密、异社团节点相互连接稀疏的特点[2-6]。为了更好地分析复杂网络的拓扑结构、理解复杂网络的功能以及预测复杂网络的行为，必须对网络结构进行社团划分。层次聚类算法作为社团发现最主要的一类方法，能够展现复杂网络中社团的层次化结构组成[7-9]。Newman[10]提出了基于局部搜索的快速复杂网络聚类算法FN，其目的是使网络模块性(modularity)评价函数即Q函数极大化[11]。Q越高，意味着划分的社团越有意义，很多社团划分方法[12-15]的目的就是将Q极大化。Guimera等[3]提出了基于模拟退火算法的复杂网络聚类算法GA，此算法具有跳过局部最优解、找到全局最优解的能力，从而具有很高的聚类精度。然而，Q函数是有偏的，并不能完全准确地刻画最优的(或者说是真实的)网络簇结构[1]。对于某些网络，其真实的网络簇结构对应的 Q是局部极大值，而非全局最大值。Guimera等[16]经进一步研究发现：对于某些随机网络，由于受到扰动的影响，明显不好的网络簇结构却对应较高的Q。为此，Fortunato[17]研究了Q函数对聚类精度的影响，指出：对于大规模复杂网络，采用这类优化方法倾向于找到粗糙的而不是精确的网络社团结构。这意味着采用这类算法未必能找到大规模网络中真正存在的全部社团，仅仅适合于小规模网络的社团划分。这种启发式复杂网络社团发现算法包括 MFC算法[18]、GN算法[2]及其改进算法[6,19]、WH算法[20]等。这些层次化社团发现算法将网络划分为不同的社团，每个点只属于1个社团。然而，在许多实际网络中，有些点可能属于多个社团，所以，若能发现可交叠的社团结构，则更具有实际意义[1]。为了找到社团间重复的点，Palla等[4]提出基于k-团的算法CPM，能够识别重叠网络社团结构。其后提出k-dense[21]算法，也可以识别重叠的网络社团结构，并且应用于各种实际网络中。但是，这些方法又不能显示出社团的层次化特性。Lancichinetti等[22]提出了 1种可以允许重叠的层次化社团发现算法。他们试图找到合适函数的局部最优解来发现重叠的社团结构，围绕1个种子节点来发现重叠社团的层次化结构。但是，由于种子节点是随机选取的，不能保证所有重叠社团都有层次结构，为此，Shen等[23]提出了一种EAGLE算法[23]，用极大团作为初始社团，根据社团的相似性，应用凝聚法来合并社团，以此找到重叠的层次化社团结构。但是，由于要重复计算社团的相似度，算法复杂度极高，很难应用于大规模的实际网络[11]。为了提高算法的运行效率，本文作者设计了一种发现层次化交叠社团的快速算法F-HOC：用极大团k-团作为初始社团，提出1个指标——社团连通性，以该指标为依据，用凝聚法对k-团进行弱社团检测，将符合条件的社团进行递归合并，以达到网络可交叠层次化快速聚类的目的。

1 发现层次化交叠社团的快速算法F-HOC

大多数层次化聚类算法在其凝聚过程中是对孤立的点进行扩展，本文提出的F-HOC算法则是从极大团开始进行扩展。由于初始的极大团中包含重复的点，所以，基于这些极大团扩展发现的社团很可能彼此交叠。在计算极大团时，有些极大团中的点分别属于其它不同的极大团，这种极大团称为附属极大团(Subordinate maximal clique)[23]。附属极大团容易误导算法，本文不予考虑。实验证明大多数附属极大团的规模比较小，因此，F-HOC先找出所有大于等于k的极大团即k-团，这样可以有效地剔除附属极大团。但是，这样可能会剔除一些比较小的非附属极大团，k越大，越可能删除更多的非附属极大团，而k越小，则越可能保留附属极大团。在实际网络中，k一般取3～6[4,23]。在剔除小于k的附属极大团后，有可能存在一些点不属于任何极大团，这些点成为附属点(Subordinate vertices)，将这些点作为单独的初始社团参与合并过程。

EAGLE算法以社团的相似性作为合并两社团的条件，但重复计算社团的相似性相当耗时；在大多数层次化聚类算法中，使用边数之类的全局变量来划分社团，而重复计算全局变量的算法时间复杂度非常高，很难应用于大型复杂网络。考虑到连接两社团间的边数越多，两社团联系越紧密，越有可能属于1个社团，本文在F-HOC算法中采用1个新的指标——社团连通性，来评价2个社团连接是否紧密。

定义1 社团连通性CAB是评价2个社团连接是否紧密的1个指标：

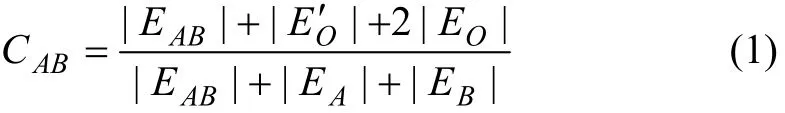
式(1)中：分子 | EAB|+|EO′ |+2|EO|为连接两社团的边数；分母 | EAB|+|EA|+|EB|为两社团的总边数。CAB越大，则表示连接两社团的边占两社团总边数的比例越大，表明两社团连接越紧密，两者越有可能属于同一个社团。

F-HOC以社团连通性指标为依据，用凝聚法对k-团进行合并判断，最终目的是所发现的社团都满足弱社团的定义。

定义 2 弱社团(Weak community)[6]是指子图 H中所有节点与H内部节点的度之和大于H中所有节点与H外部节点连接的度之和。给定1个无向简单图G和1个子图H( H ⊆ G )，H满足弱社团的定义，当且仅当：

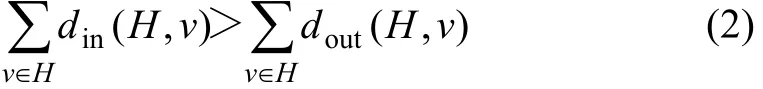
其中：v为H中的节点；din(H,v)为v的内度；dout(H,v)为v的外度。

基于社团连通性和弱社团的量化定义，提出一种基于连通性的发现交叠社团的快速层次化算法F-HOC。

Input: 无向无权简单图G=(V,E)，初始极大团规模k；

Output: 可交叠的层次化社团。

步骤1 找出所有规模≥k的极大团，附属点视为独立初始社团。

步骤 2 对两两相连的社团采用 CAB进行判断；对CAB进行降序排列，放入队列CC中。

步骤3 依次判断Cc中每2个社团是否合并。

(1) 若2个社团都不满足弱社团的定义，则合并2个社团；

(2) 合并2个社团后，将这个CAB从队列CC中移除，且将与新合并社团有连接的社团的CAB进行重新计算，将队列CC重新排序；

步骤4 对不满足合并条件的社团不进行处理。

步骤5 按CC的排序执行步骤3和4，直到队列CC为空为止。

步骤6 输出层次化合并的可交叠社团。

F-HOC的输入是1个无向无权简单图G=(V,E)。首先用经典的Bron-Kerbosch算法[24]找到所有极大团，过滤图中的规模小于k的极大团，剩下规模大于等于k的每个极大团视为1个初始社团，附属点也视为独立的初始社团。然后计算两两相连社团的社团连通性，其值越大，表明2个社团越有可能属于同一个社团。根据计算所得的社团连通性值进行降序排列，放入队列CC中，从大到小分别判断两社团是否满足弱社团定义。只有在2个社团都不满足时才合并，直到队列CC为空为止，整个层次化聚类过程结束，输出得到的所有的社团，包括合并过程和最终的社团。可根据合并过程画出层次化社团树状图，以展示复杂网络中社团的层次化组织结构。

因为F-HOC算法是利用社团连通性进行判断，只需计算局部变量，其时间复杂度比EAGLE用全局变量计算的低。EAGLE 的时间复杂度[23]为O(n2+(h+n)s+n2s) (不计计算极大团的时间，其中，n为点的个数，s为初始社团k-团的个数，h为邻居社团对(两两相连社团对或者是相似社团对)的个数)。F-HOC中，计算所有邻居社团对社团连通性的时间复杂度为 O(h)，重复合并的时间复杂度为 O(h2(s-1))，整个算法的时间复杂度为 O(h2s)(同样不计计算极大团的时间)。比较EAGLE的时间复杂度，h远小于n，所以，F-HOC更适用于大型的复杂网络。

2 实验结果及其分析

采用已知社团结构的随机网络进行测试[1]，比较F-HOC和EAGLE的精度和速度。已知社团结构的随机网络定义为RN(C, b, d, pin)(其中：C为网络社团的个数；b为每个社团包含节点的个数；d为网络中节点的平均度；pin为社团内连接密度(即社团内连接总数与网络连接总数的比值))。pin越大，随机网络的社团结构越明显，反之，社团结构越模糊。特别地，当pin＜0.5时，认为该随机网络不具有社团结构。实验采用被普遍接受的基准随机网络RN(4, 32, 16, pin)作为标准数据，k取4，并设定了2个点为重叠点。

2.1 算法的敏感度

敏感度Sn是用来评估社团识别精度的重要指标[25]，是指已知社团中被算法发现出来的部分所占比例：

其中：PT(True positive)表示算法识别出来的社团 Cp与已知社团Ck匹配程度OS(Cp, Ck)超过匹配度阈值的数量；NF(False negative)表示已知社团中没有被识别出来的数量。

算法识别出来的社团(Predicted community, Cp)与已知社团(Known community, Ck)的匹配程度OS(Cp, Ck)的计算公式[25-26]为：

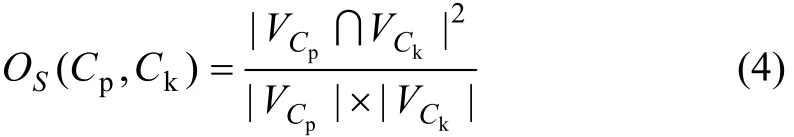
若 Cp和 Ck的匹配程度 OS(Cp, Ck)超过给定的阈值，则称这2个社团匹配。对于已知社团Ck，若识别出的社团Cp与之匹配程度OS(Cp, Ck)超过给定阈值，则称该已知社团被标识；若OS(Cp, Ck)=1，则称该社团被完全标识。

图1所示表示pin取0.9，0.8和0.7时，F-HOC和EAGLE在不同匹配阈值OS下的匹配精度Sn，匹配精度用敏感度来表示，曲线上的每个数据点是两算法识别 50个已知社团结构的随机网络得到的平均 Sn。从图 1可以看出：在网络社团性很强的情况下，即 pin为0.9和0.8时，F-HOC算法的敏感度与EAGLE算法的敏感度相差不多，都比较高。这也说明 F-HOC算法与EAGLE算法在网络社团性较明显的情况下，两算法都能准确地识别出已知社团。当pin为0.7时，F-HOC算法的敏感度随着匹配阈值的增加开始下降，这与大多数复杂网络聚类算法的结果类似[1]，在网络社团性不是很强的情况下，识别能力开始显著降低。

图1 不同匹配阈值下F-HOC与EAGLE的敏感度Sn的比较Fig.1 Comparison of Sn of F-HOC and EAGLE with respect to different overlapping score thresholds

2.2 算法的速度

算法的速度是评价聚类算法的重要指标。本文比较分析了F-HOC和EAGLE 2种算法在相同规模、不同社团性网络下的运行时间以及不同规模网络下的运行时间，如表1和图2所示。表1所示表示pin取0.9～0.5时，F-HOC和EAGLE识别50个随机网络得到的平均时间；图2所示为不同规模下算法的运行时间。选用的测试网络是随机网络RN(4, b,16,0.8)。该网络由社团结构确定，但其规模可由b来调节，共包含4b个网络节点，64b条网络连接。当b =1 024时，EAGLE的运行时间超过了48 h还没有得出结果，所以没有被列出。

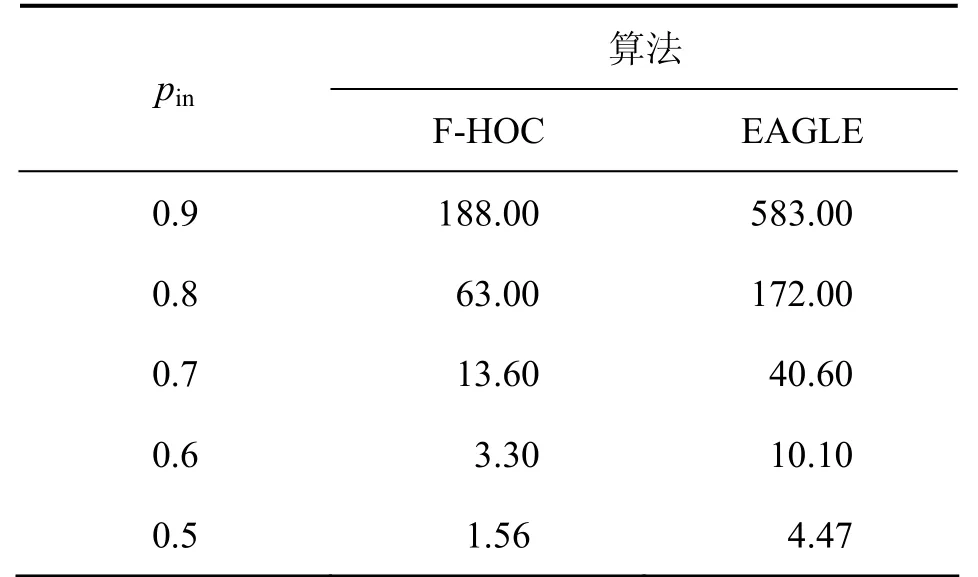
表1 不同网络社团性下F-HOC与EAGLE算法的运行时间比较Table 1 Comparison of time of F-HOC and EAGLE with respect to different network connections s

从表 1可以看出：不管网络社团性是否明显，F-HOC的运行效率都比 EAGLE的高很多。因为F-HOC算法是利用社团连通性进行判断，只需计算局部变量，计算复杂度较低，所以，不论网络社团性如何，F-HOC的速度都比EAGLE的速度快。如图2所示，不管网络规模如何，F-HOC比EAGLE的速度快很多，且随着网络规模的增加，EAGLE的运行时间提升幅度比F-HOC的时间提升幅度快很多，而F-HOC时间变化幅度不大。网络的规模越大，F-HOC的优势越明显。而在实际网络中，网络节点一般都在 1 000以上，且随着大规模网络数据的不断增加，F-HOC更适用于大规模的复杂网络。

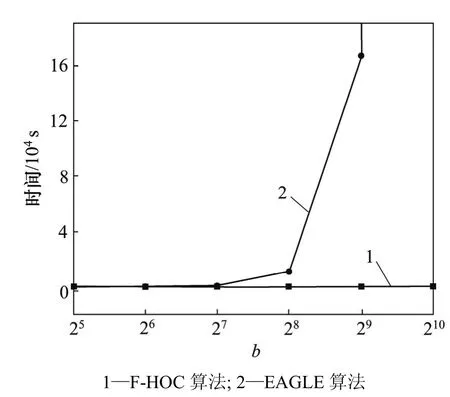
图2 不同网络规模下F-HOC与EAGEL的运行时间比较Fig.2 Comparison of time of F-HOC and EAGLE with respect to different sizes of networks

2.3 交叠点的识别度

因为算法可以用于识别交叠的模块，在生成已知社团结构的随机网络时，加入了1个重叠参数，即在生成随机网络时保证社团之间有重叠点。为了验证算法识别社团的交叠性能力，检查了设定的重叠点是否出现在多个输出社团内，若都找到，则令Ol=1；若有1个没有找到，则令Ol=0，得出对已知交叠点的识别度Ov：

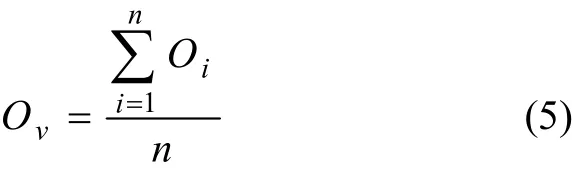
其中：n表示随机网络的个数。表2所示为pin取0.9～0.5时，F-HOC和EAGLE对已知交叠点的识别度。从表2可以看出：在网络社团性很强的情况下即pin为0.9和0.8时，F-HOC和EAGLE都能准确地识别出已知的重叠点，也就是说算法确实找到了这些重叠的点，并且这些点都存在于多个社团内。但随着网络社团性的减弱，识别重叠点的能力也明显降低，这与识别社团的能力呈正比。

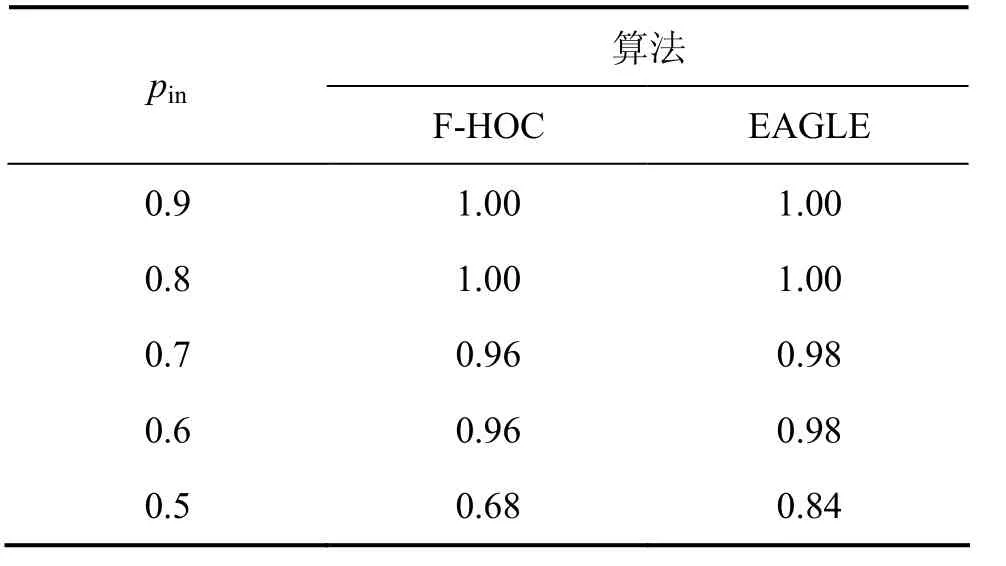
表2 不同网络社团性下F-HOC与EAGLE算法对已知交叠点的识别度OvTable 2 Comparison of Ov of F-HOC and EAGLE with respect to different network connections

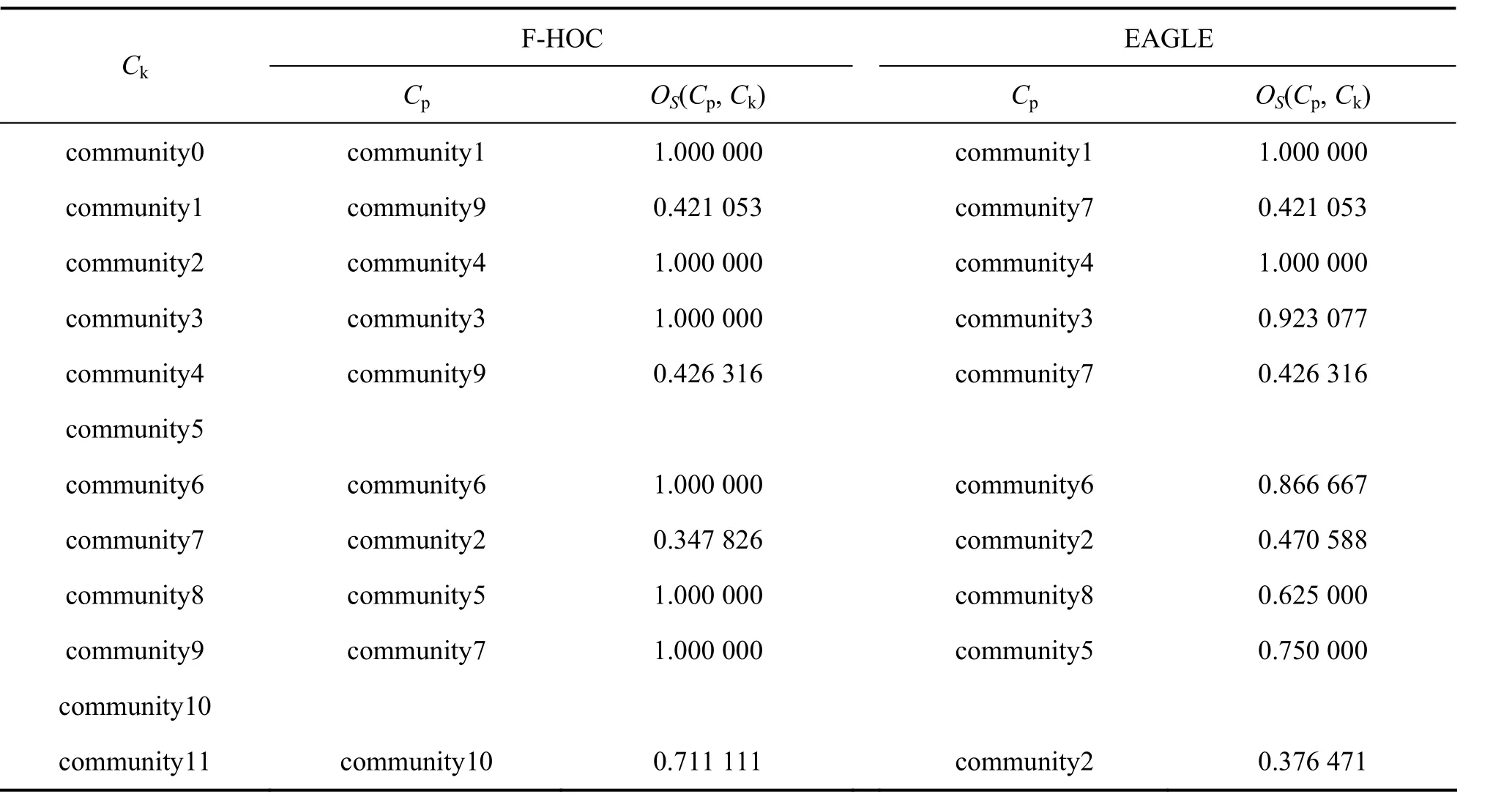
表3 F-HOC与EAGLE算法应用于足球网络的匹配度对照结果Table 3 Comparison of overlapping scores which applying F-HOC and EAGLE in football network

3 应用

将F-HOC算法应用于社团性较强的足球网络[2]，并与EAGLE的结果进行比较，结果如表3所示。表3中列出了所有OS(Cp, Ck)≥0.2的社团对和其社团匹配值，足球网络有12个社团。从表3可以看出：F-HOC找到了 10个社团，其中与已知社团完全匹配的有 6个，占已知社团的50%；匹配值高于0.500 000的有7个，占已知社团的58%。EAGLE找到了8个社团，其中与已知社团完全匹配的只有2个，仅占已知社团的17%；匹配值高于0.500 000的有6个，占已知社团的 50%。这也说明在社团性明显的实际网络中，F-HOC的精度比EAGLE的精度高。

F-HOC算法的运行时间为3.547 s，EAGLE算法的运行时间为9 490 s，可见，F-HOC的运行速度明显增大。

4 结论

(1) 设计了一种发现交叠社团的快速层次化算法F-HOC。以提出的度量社团间连通性的指标为依据，采用凝聚法对k-团进行弱社团检测，对符合条件的社团进行合并，递归合并以达到网络可交叠层次化快速聚类的目的。

(2) F-HOC以极大团为初始社团，在此基础上进行合并，所以，社团都存在交叠性。

(3) F-HOC利用社团连通性这一指标进行判断，计算复杂度比EAGLE采用的社团相似度这一全局变量低，所以，不论网络社团性如何，速度都比EAGLE的运行速度快，有明显的优势；且随着网络规模的增大，F-HOC运行时间的增幅比EAGLE运行时间的增幅小很多。

(4) 在网络社团性强的情况下，F-HOC能准确识别出已知的社团结构和重叠点，精度与EAGLE的精度相当；但是，在社团性较弱的情况下，虽然速度比EAGLE的快，但是，识别能力比EAGLE的弱。由于EAGLE是利用Q函数来划分社团性的，对于明显不好的网络簇结构，EAGLE也有可能得出较高的Q，所以，F-HOC在社团性不是很强的情况下，识别能力比EAGLE的弱并不能说明F-HOC的识别能力差。

(5) 总体来说，对于大规模的社团结构明显的复杂网络，用F-HOC算法发现可交叠的层次化社团结构具有很高的精度和运行效率。

[1] 杨博, 刘大有, LIU Ji-ming, 等. 复杂网络聚类方法[J]. 软件学报, 2009, 20(1): 54-66.YANG Bo, LIU Da-you, LIU Ji-ming, et al. Complex network clustering algorithms[J]. Journal of Software, 2009, 20(1):54-66.

[2] Girvan M, Newman M E J. Community structure in social and biological networks[J]. Proc of the National Academy of Science,2002, 99(12): 7821-7826.

[3] Guimera R, Amaral L A N. Functional cartography of complex metabolic networks[J]. Nature, 2005, 433(2): 895-900.

[4] Palla G, Derenyi I, Farkas I, et al. Uncovering the overlapping community structures of complex networks in nature and society[J]. Nature, 2005, 435(6): 814-818.

[5] Wilkinson D M, Huberman B A. A method for finding communities of related genes[J]. Proc of the National Academy of Science, 2004, 101(Suppl 1): 5241-5248.

[6] Radicchi F, Castellano C, Cecconi F, et al. Defining and identifying communities in networks[J]. Proc of the National Academy of Science, 2004, 101(9): 2658-2663.

[7] Sales-Pardo M, Guimerà R, Moreira A A, et al. Extracting the hierarchical organization of complex systems[J]. Proc of the National Academy of Science, 2007, 104(39): 15224-15229.

[8] Ravasz E, Somera A L, Mongru D A, et al. Hierarchical organization of modularity in metabolic networks[J]. Science,2002, 297(8): 1551-1555.

[9] Pons P. Post-processing hierarchical community structures:Quality improvements and multi-scale view[EB/OL].[2006-08-09]. http://arxiv.org/ps_cache/cs/pdf/0608/0608050 v1.pdf.

[10] Newman M E J. Fast algorithm for detecting community structure in networks[J]. The European Physical Journal B, 2004,38(6): 321-330.

[11] Newman M E J. Girvan M. Finding and evaluating community structure in networks[J]. Physical Review E, 2004, 69(2):026113-1-026113-15.

[12] Wang Z, Zhang J. In serach of the biological significance of modular structures in protein networks[J]. PLOS Computational Biology, 2007, 3(6): 1011-1021.

[13] Newman M E J. Modularity and communities structure in networks[J]. Proc of the National Academy of Science, 2006,103(23): 8577-8582.

[14] Pujol J M, Béjar J, Delgado J. Clustering algorithm for determining community structure in large networks[J]. Physical Review E, 2006, 74(1): 016107-1-016107-9.

[15] Duch J, Arenas A. Community detection in complex networks using extreme optimization[J]. Physical Review E, 2005, 72(2):027104-1-027104-4.

[16] Guimera R, Sales M, Amaral L A N. Modularity from fluctuations in random graphs and complex networks[J].Physical Review E, 2004, 70(2): 025101-1-025101-8.

[17] Fortunato S, Barthelemy M. Resolution limit in community detection[J]. Proc of the National Academy of Science, 2007,104(1): 36-41.

[18] Flake G W, Lawrence S, Giles C L, et al. Self-Organization and identification of Web communities[J]. IEEE Computer, 2002,35(3): 66-71.

[19] Tyler J R, Wilkinson D M, Huberman B A. Email as spectroscopy: Automated discovery of community structure within organizations[J]. The Information Society, 2005, 21(2):143-153.

[20] Wu F, Huberman B A. Finding communities in linear time: A physics approach[J]. European Physical Journal B, 2004, 38(2):331-338.

[21] Saito K, Yamada T, Kazama K. Extracting communities from complex networks by the k-dense method[J]. IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences, 2008, E91-A(11): 3304-3311.

[22] Lancichinetti A, Fortunato S, Kertesz J. Detecting the overlapping and hierarchical community structure of complex networks[EB/OL]. [2009-05-11]. http://arxiv.org/ps_cache/arxiv/pdf/0802/0802.1218 v2.pdf.

[23] SHEN Hua, CHENG Xue, CAI Kai, et al. Detect overlapping and hierarchical community structure in networks[J]. Physica A,2009, 388: 1706-1712

[24] Bron C, Kerbosch J. Finding all cliques in an undirected graph[J].Communications of the ACM, 1973, 16(9): 575-577.

[25] Bader G D, Hogue C W. An automated method for finding molecular complexes in large protein interaction networks[J].BMC Bioinformatics, 2003, 4(2): 1-27.

[26] King A D, Przulj N, Jurisica I. Protein complex prediction via cost-based clustering[J]. Bioinformatics, 2004, 20(17):3013-3020.