负载下CFRP与钢板复合加固钢筋混凝土梁抗弯试验及设计理论
2010-05-31熊学玉范新海
熊学玉 ,范新海
(1. 同济大学 建筑工程系,上海,200092;2. 同济大学 先进土木工程材料教育部重点实验室,上海,200092)
粘贴碳纤维复合材料 (Carbon fiber reinforced polymer,CFRP)与外粘钢板是加固修补混凝土结构技术中应用较为广泛且受力机理研究较为成熟的2种加固方式。两者在改善结构受力性能上各有优缺点[1-10]:(1) CFRP抗拉强度设计值一般为1.40~2.30 GPa,钢板抗拉强度设计值为0.23~0.40 GPa,CFRP抗拉强度几乎是钢板的10倍,所以,在相同的粘贴量下,CFRP加固后构件承载力大于钢板;(2) CFRP和钢材弹性模量基本一致,达到相同的应力时,钢材的截面要比CFRP的截面大得多,所以,粘钢板法加固提高构件刚度的幅度要超过 CFRP加固的幅度;(3) CFRP应力-应变关系为线性关系,破坏时没有屈服台阶,延伸率较低,加固后构件一般呈脆性破坏;钢板为理想的弹塑性材料,延伸率较高,加固后构件一般呈延性破坏。结合两者在改善结构受力性能上的优点,将CFRP与钢板复合加固受弯构件,可弥补单一材料加固的不足,具有一定工程应用价值。已有复合加固试验研究结果表明[11-12]:复合加固梁的承载力和刚度显著提高,且复合加固梁破坏时具有较好的延性。但大部分试验研究是在无负载进行的,而实际加固工程中,加固前受弯构件一般都处在一定的负载水平,即使加固前进行卸载也很难做到完全卸载,因此,有必要对负载下复合加固梁进行试验研究。
1 试验方法
共设计4根试件, 3根钢筋混凝土梁,采用CFRP与钢板复合加固,1根为对比试件。梁截面尺寸(宽×高)为150 mm×250 mm,长为2.6 m,净跨l0=2.4 m,2根梁底受拉钢筋为2级钢,直径为12 mm,剪跨区箍筋直径为8 mm。试件示意图见图1(其中:P为负载)。混凝土设计强度为C40,实测混凝土立方体抗压强度平均值为 47.6 MPa;CFRP实测抗拉强度 fcf,u=4.240 GPa,弹性模量Ecf=2.25×1011Pa,宽度bcf=150 mm,厚度tcf=0.111 mm;钢板型号为Q235,实测抗拉强度fpy=290 MPa,宽度bp=150 mm,厚度tp=3 mm,CFRP与钢板通长粘贴于梁底。复合加固梁加固及锚固方式见图2及表1。

图1 试验梁的截面尺寸及配筋情况Fig.1 Details of specimen

图2 试验梁方式及锚固形式Fig.2 Retrofit and anchorage mode of test beams

表1 试验梁的加固及锚固方案Table 1 Retrofit and anchorage mode of test beams
试验测试内容包括:位移(跨中、分配梁2支座位置)、纤维应变、梁纵筋应变、混凝土应变、裂缝开展情况。加载方式采用液压千斤顶三分点二集中力加载,梁受拉侧表面打磨后,按照表1所示的加载历史分级加载到预先确定的荷载等级,然后保持该荷载不变,粘贴CFRP与钢板加固,待粘结胶达到黏结强度后再分级连续加载至构件破坏。
2 试验结果及分析
2.1 梁承载力分析
梁受弯承载力如表2所示。从表2可知:与未加固梁相比,复合加固梁的屈服荷载及极限荷载都显著提高,屈服荷载提高 177%~182%,极限荷载提高194%~200%。可见,采用CFRP与钢板复合加固不仅显著地提高了梁的极限荷载,而且有效提高了梁的屈服荷载。这主要是因为:在钢筋屈服之前,CFRP与钢板及钢筋的应力应变随荷载同步增长,由于钢板截面积较大,所以,屈服荷载显著提高。
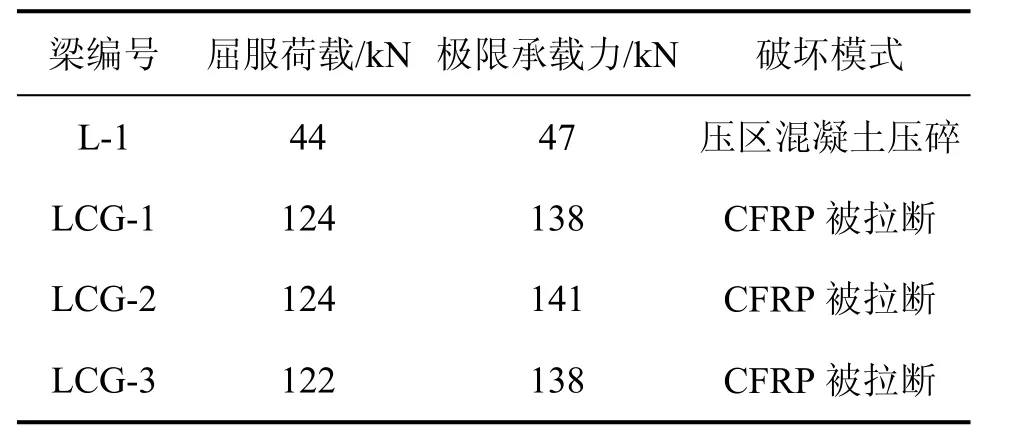
表2 梁受弯承载力Table 2 Load-carrying capacities of test beams
对比梁LCG-1,LCG-2和LCG-3的承载力可知:负载对加固后梁的屈服荷载和极限荷载影响比较小,一般在10%以内,因此,在承载力计算时,可忽略负载的影响。
2.2 梁刚度变化分析
图 3所示为梁荷载-挠度曲线。从图 3可以看出:试验梁的荷载与挠度曲线为四折线,转折点分别发生在混凝土开裂和加固前负载点、钢筋及钢板屈服点。CFRP与钢板复合加固后梁的抗弯刚度显著提高,且加固梁破坏时具有一定的延性。在相同荷载下,加固梁的挠度小于未加固梁的挠度,减小幅度与负载有关。
对比梁LCG-1,LCG-2和LCG-3荷载-挠度曲线可知:在相同的荷载作用下,负载水平越大,加固梁的跨中挠度越大,例如,在60 kN荷载作用下,梁LCG-1,LCG-2和LCG-3跨中挠度分别为4.17,4.87和6.48 mm。可见:在钢筋或钢板屈服前,负载对加固后梁的刚度影响比较大。
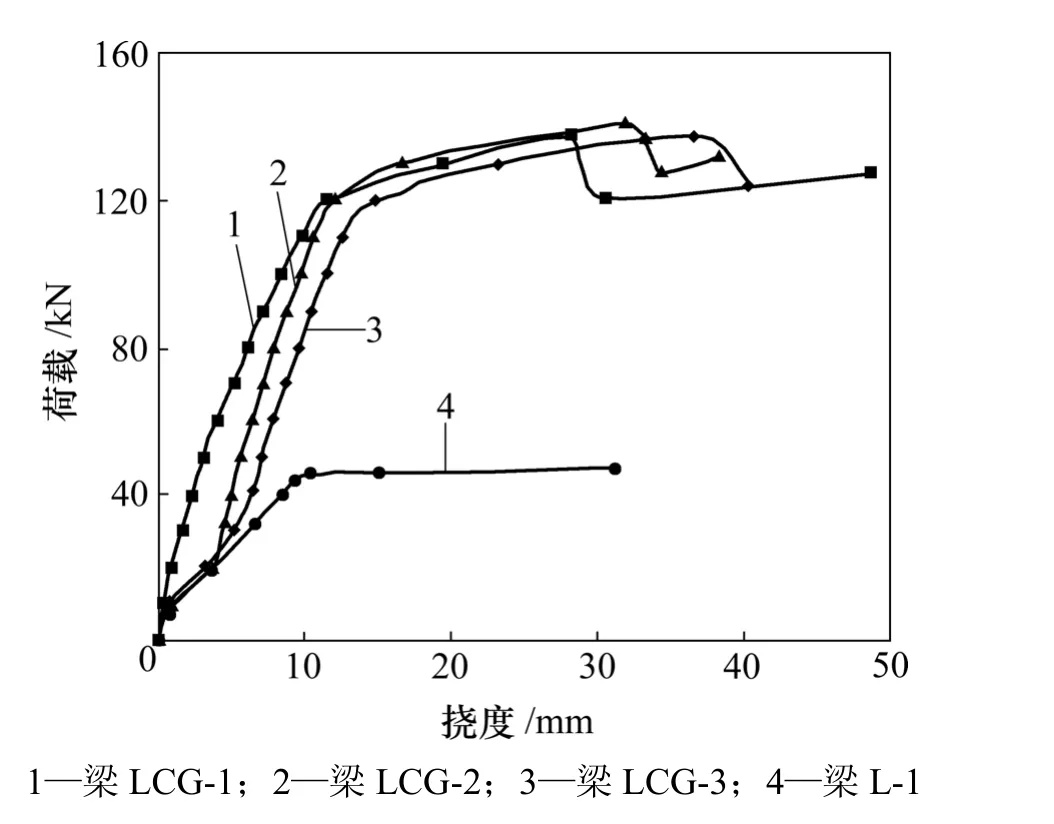
图3 梁荷载-挠度曲线Fig.3 Load-deflection curves of beams
2.3 梁裂缝分析
极限破坏时各梁裂缝分布如图4所示。从试验梁的受力过程和裂缝开展情况(图4)来看:构件最终破坏时,复合加固梁的裂缝均要比未加固梁L-1的裂缝小且裂缝间的平均间距小,说明采用CFRP与钢板复合加固能有效地抑制裂缝的开展。在负载下,复合加固梁一般总是先出现几条主裂缝,随着荷载的增加,在主裂缝两侧出现斜裂缝,这些斜裂缝斜向上开展,最后与中间的主裂缝交汇。梁LCG-1的裂缝比梁LCG-2和LCG-3的裂缝多,裂缝的宽度和平均的间距较小,裂缝长度较短。这主要是因为无负载下,CFRP与钢板复合加固对梁裂缝的抑制作用发挥比较早。可见:负载对加固梁的裂缝的开展和发展有一定的影响。在相同荷载作用下,负载越大,加固后梁的裂缝宽度和平均间距越大,裂缝的长度越长。

图4 极限破坏时各梁裂缝分布Fig.4 Crack distribution figures of beams at ultimate failure
本次试验加固梁的破坏均为CFRP拉断,在破坏前有“噼啪”的响声,未见CFRP与试验梁发生剥离破坏,最终破坏时,CFRP的极限拉应变都达到 0.01以上。可见:采用有效的附加锚固能有效地延缓剥离破坏的发生。
3 复合加固梁受弯承载力的计算
3.1 基本假设
(1) 本次试验和已有的试验结果表明[12]:复合加固梁在整个受力过程中,截面混凝土、钢筋、钢板及CFRP应变分布符合平面假定。
(2) 钢板和钢筋应力-应变关系为理想弹塑性材料的应力-应变关系,CFRP应力-应变关系为线弹性材料的应力-应变关系[13-14]。
(3) 混凝土的应力-应变曲线采用Rüsch建议关系曲线,不考虑开裂后混凝土的抗拉强度[15]。
(4) 粘贴 CFRP与钢板复合后厚度较小,忽略其厚度对梁高的影响。
3.2 破坏模式
CFRP与钢板复合加固梁的最终破坏模式与负载、CFRP及钢板粘贴量和锚固方式有关,最终复合加固梁的破坏模式为:
(1) 钢筋及钢板屈服后,CFRP达到允许拉应变,此时,受压区混凝土尚未压碎。
(2) 钢筋及钢板屈服后,混凝土被压碎,此时,CFRP未达到其允许拉应变。
(3) 钢筋或钢板未屈服时,混凝土被压碎,CFRP未达到允许拉应变。
(4) 在达到正截面极限承载力前,CFRP与混凝土发生剥离破坏。
在这几种破坏模式中,剥离破坏可以采用有效的锚固方式避免其发生;第3种破坏属于超筋破坏,设计时应避免。因此,对于CFRP与钢板复合加固梁受弯承载力的计算主要针对第1种和第2种破坏模式。
3.3 界限破坏的判定
3.3.1 界限破坏Ⅰ(钢筋及钢板都屈服时,混凝土被压碎)
在混凝土压碎前,钢板及钢筋均要屈服。由于负载和加固量不同,有可能钢筋先屈服然后钢板后屈服,也有可能相反。由平截面假定,混凝土受压区高度xcb如下。
对钢板后屈服:
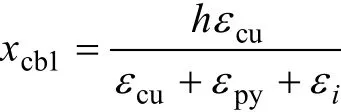
对钢筋后屈服:
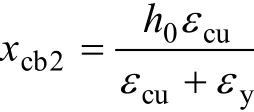
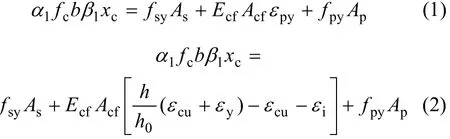
式中:εi为CFRP及钢板滞后应变,可按参考文献[9]中的方法计算;Ecf为CFRP的弹性模量;fsy和 fpy分别为钢筋、钢板的屈服强度;fc为混凝土强度设计值;εcu为混凝土极限抗压应变;εy和εpy分别为钢筋、钢板的屈服应变;As,Ap和Acf分别为钢筋、钢板、CFRP截面面积;1α和1β按文献[15]取值。当混凝土强度等级为C50以下时,1α=1.0,1β=0.8。
在CFRP与钢板复合加固设计时,应保证xc<xcb,避免发生超筋破坏。
3.3.2 界限破坏Ⅱ(混凝土压碎与CFRP拉断界限)
在钢筋及钢板都屈服的前提下,CFRP拉断的同时混凝土被压碎。由平截面假定,临界受压区混凝土高度xcfb为:
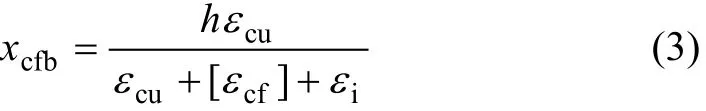
由力平衡式(4)确定受压区混凝土高度xc:
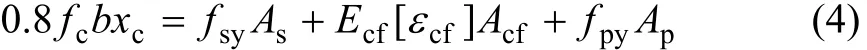
式中:[εcf]为CFRP极限拉应变允许值,一般取0.01。当受压区高度xc<xcfb时,破坏形态为碳纤维布拉断,即第1种破坏形态;当受压区高度xc>xcfb时,破坏形态为受压区混凝土被压碎,即第2种破坏形态。
3.4 受弯承载力计算
3.4.1 受压区混凝土压碎时承载力的计算
当梁的破坏状态为受压区混凝土压碎时,受压区混凝土应力可等效矩形计算。由力的平衡可求解相对受压区混凝土高度x:
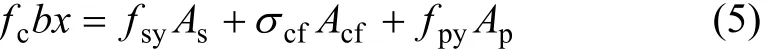
则加固梁极限承载力Mu为:
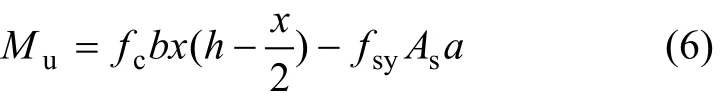
3.4.2 CFRP拉断时承载力的计算
当梁的破坏状态为CFRP拉断时,受压区混凝土未被压碎,受压区混凝土合力和合力点位置可能出现2种情况。为防止复杂的受压区混凝土合力计算,使计算公式简化且偏保守,受压区混凝土高度xc取界限破坏Ⅱ时混凝土的受压区高度 xcfb,即 xc=则CFRP拉断破坏时,加固梁极限弯矩Mu为:
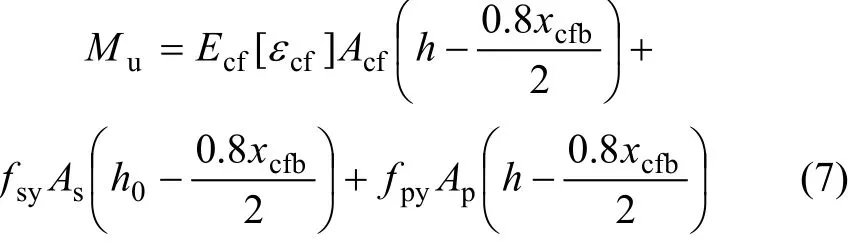
3.5 理论计算公式的验证
应用上述公式对试验梁进行理论计算,计算结果如表3所示。
从表3可以看出:理论计算值与试验值较吻合,验证该理论计算公式的可行性。
4 正常使用下挠度计算
根据负载下复合加固梁荷载-挠度曲线关系,将负载下复合加固后梁在正常使用下挠度分为2个阶段即复合加固前和复合加固后进行计算,则复合加固后梁总挠度为:

式中:f1为复合加固前荷载产生的挠度,按其普通钢筋混凝土受弯构件计算其变形[15];f2为复合加固后再次加荷载产生的挠度,其复合加固后梁截面抗弯刚度按式(9)计算。
复合加固后梁的截面抗弯刚度为:

不同负载时挠度的理论计算值与试验值对比如图5和图6所示。
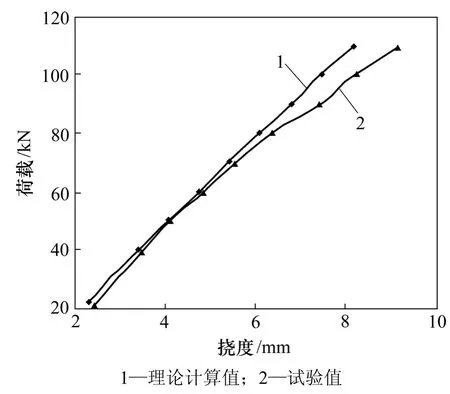
图5 负载50% Mu下梁的荷载-挠度曲线Fig.5 Load-deflection curves of beam under 50% Mu preloaded
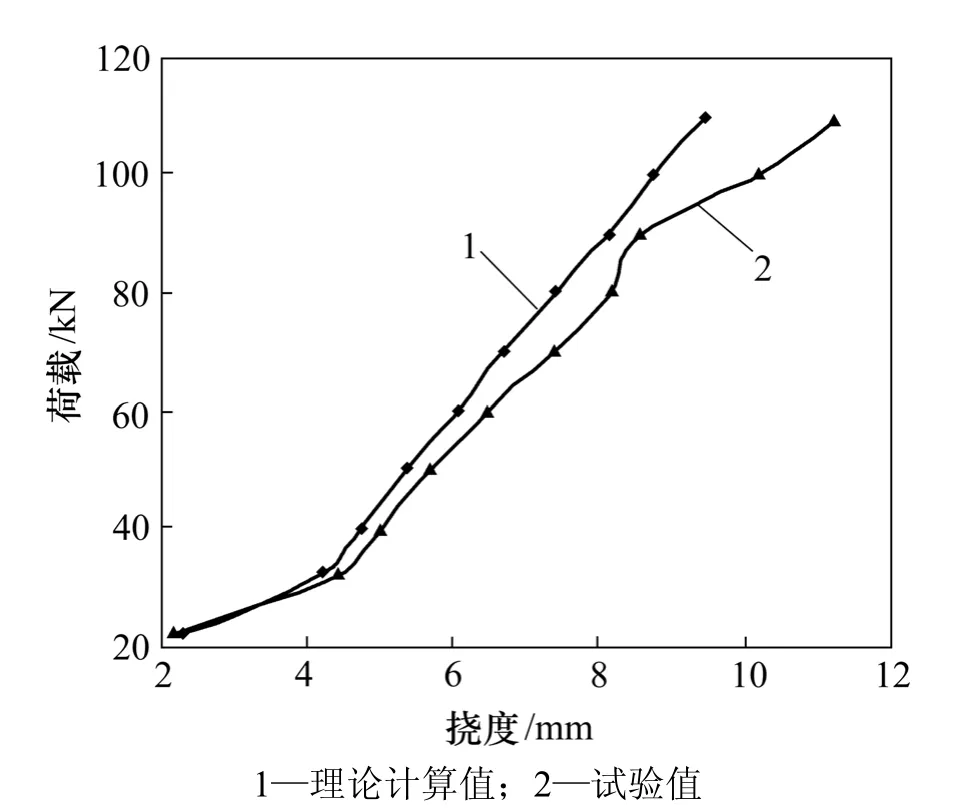
图6 负载70% Mu下梁的荷载-挠度曲线Fig.6 Load-deflection curves of beam under 70% Mu preloaded
从图5与图6可知:在正常使用条件下,复合加固梁的挠度理论计算值与试验值较吻合。
5 裂缝宽度计算
无负载时,由于CFRP与钢板复合加固后的梁裂缝间距比一般混凝土梁的裂缝间距小,因此,在《混凝土结构设计规范》(GB 50010—2002)[15]中关于最大裂缝宽度计算公式的基础上乘以裂缝间距折减系数α1,根据实测裂缝间距与对比梁裂缝间距的比值取α1=0.7;考虑到初始荷载的影响,再在此基础上乘以1个负载影响系数αm,经LCG-2,LCG-3与LCG-1裂缝间距对比最终复合加固梁的最大裂缝宽度计算公式为:
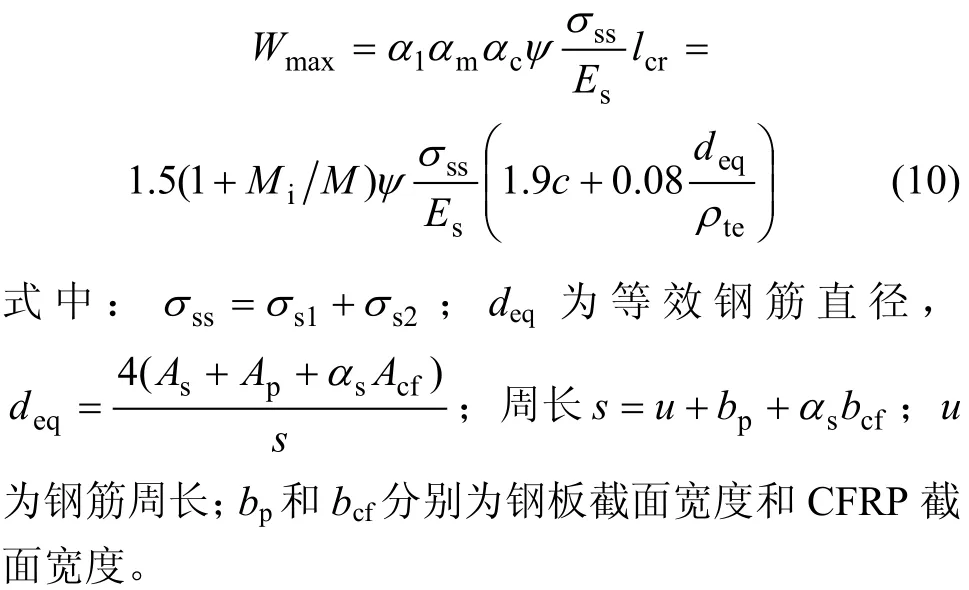
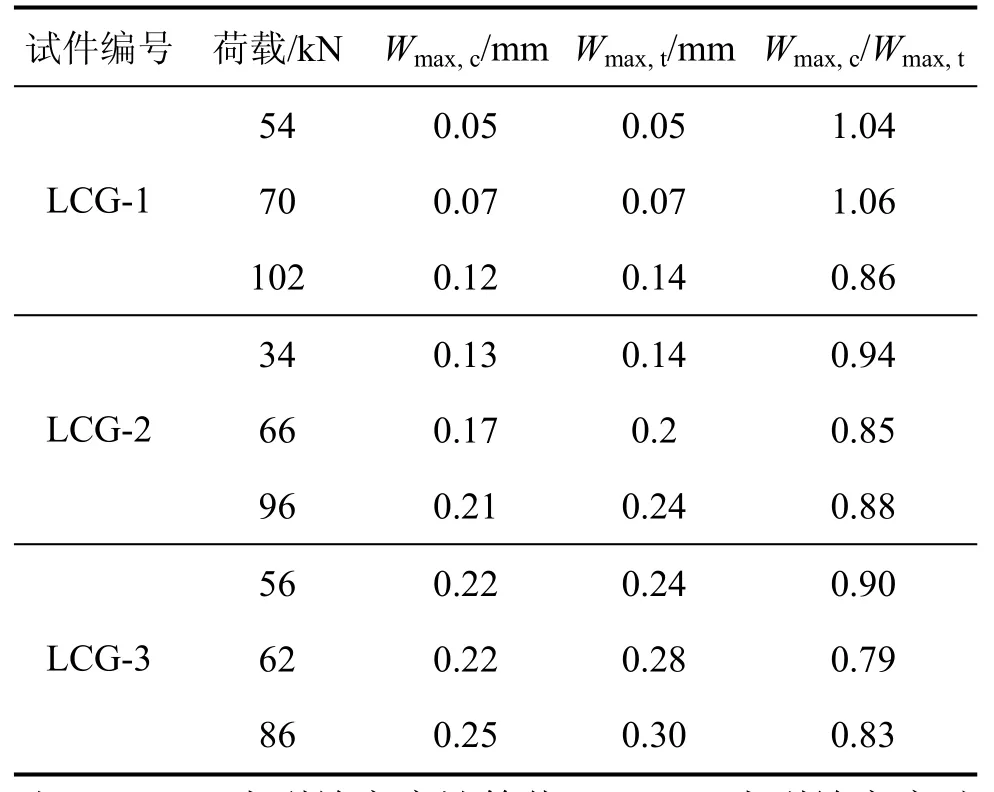
表4 裂缝宽度理论计算值与试验值对比Table 4 Comparison of crack width between calculated values and test results
裂缝宽度计算值与试验值比值的平均值为0.905,标准差为0.092,说明计算结果具有较高的精度,可以用于计算正常使用阶段复合加固梁的最大裂缝宽度计算。
6 结论
(1) 与未加固梁相比,采用 CFRP与钢板复合加固梁的抗弯承载力显著提高,屈服荷载提高177%~182%,极限荷载提高 194%~200%。且负载对承载力影响较小,一般在10%以内,可以忽略负载。
(2) 与未加固梁相比,采用 CFRP与钢板复合加固梁的截面抗弯刚度显著提高,挠度显著减小。在相同荷载下,挠度可减小24%~70%,且破坏时加固后梁具有较好的延性。
(3) 负载对 CFRP与钢板复合加固梁的截面抗弯刚度、裂缝宽度影响显著。在相同荷载下,加固前负载越大,挠度越大,裂缝越宽。考虑到加固后结构的使用性能要求,在实际加固工程中要尽量卸载。
(4) 最大裂缝宽度计算公式具有较高的计算精度,可用于CFRP与钢板复合加固钢筋混凝土梁的截面承载力、挠度及裂缝最大宽度的计算。
[1] Arduini M, Nanni A. Behavior of pre-cracked RC beams strengthened with carbon FRP sheets[J]. Journal of Composites for Construction, 1997, 1(2): 63-70.
[2] Ochola R O, Marcus K, Nurick G N, et al. Mechanical behavior of glass and carbon fiber reinforced composites at varying strain rates[J]. Composite Structures, 2004, 63(3/4): 455-467.
[3] Shin Y S, LEE C D. Flexural behavior of reinforced concrete beams strengthened with carbon fiber reinforced polymer laminates at different levels of sustaining load[J]. ACI Structural Journal, 2003, 100(2): 231-239.
[4] 李贵炳, 张爱晖, 金伟良. 钢筋混凝土梁加固时的既有荷载对其抗弯性能的影响[J]. 土木工程学报, 2006, 39(1): 13-20.LI Gui-bing, ZHANG Ai-hui, JIN Wei-liang. Effect of sustaining load level on flexural behavior of RC beams retrofitted with CFRP sheets[J]. China Civil Engineering Journal,2006, 39(1): 13-20.
[5] Swamg R N, Jones R, Bloxham J W. Structural behavior of reinforced concrete beams strengthened by epoxy-bonded steel plates[J]. The structural Eng, 1987, 65(2): 59-68.
[6] 欧新新, 张文华, 王纪峰. 钢筋混凝土梁粘钢加固受弯性能强度研究[J]. 浙江工业大学学报, 1999, 27(1): 23-27.OU Xin-xin, ZHANG Wen-hua, WANG Ji-feng. Research of bending behavior and bearing power of the concrete inforcement beams with steel bonded reinforcement[J]. Journal of Zhejiang University of Technology, 1999, 27(1): 23-27.
[7] 王天稳, 王晓光, 刘利珍. 粘钢加固混凝土梁裂缝宽度验算[J]. 武汉水利电力大学学报, 1997, 30(2): 102-104.WANG Tian-wen, WANG Xiao-guang, LIU Li-zhen. Crack width calculation of RC beam with steel-bonded reinforcement[J]. Journal of Wuhan University of Hydraulic and Electric Engineering, 1997, 30(2): 102-104.
[8] Abdalla H A. Evaluation of deflection in concrete members reinforced with fiber reinforced polymer(FRP) bars[J].Composite Structures, 2002, 56(1): 63-71.
[9] 周朝阳, 胡志海, 贺学军, 等. 内嵌式碳纤维板条与混凝土粘结性能的拉拔实验[J]. 中南大学学报: 自然科学版, 2007,38(2): 357-361.ZHOU Chao-yang, HU Zhi-hai, HE Xue-jun, et al. Bond behavior of NSM CFRP plate-concrete interface in pull-out experiment[J]. Journal of Central South University: Science and Technology, 2007, 38(2): 357-361.
[10] ACI 440. 2R-2002, Design and construction of externally bonded FRP systems for strengthening concrete structures[S].
[11] Dat D, Monica S. Strength and ductility of concrete beams reinforced with carbon fiber-reinforced polymer plates and steel[J]. Journal of Composites for Construction, 2004, 8(1):59-69.
[12] 卢亦焱, 周婷. 碳纤维布与钢板复合加固钢筋混凝土梁抗弯性能试验研究[J]. 铁道学报, 2006, 28(1): 80-87.LU Yi-yan, ZHOU Ting. Experimental research on flexural performance of reinforced concrete beams combination strengthened with bonded carbon fiber reinforced Polymer and steel plates[J]. Journal of the China Railway Society, 2006, 28(1):80-87.
[13] CECS 146: 2003, 碳纤维片材加固混凝土结构技术规程[S].CECS 146: 2003, Technical specification for strengthening concrete structures with carbon fiber reinforce polymer laminate[S].
[14] GB 50367, 混凝土结构加固设计规范[S].GB 50367, Design code for strengthening concrete structure[S].
[15] GB 50010—2002, 混凝土结构设计规范[S].GB 50010—2002, Code for design of concrete structures[S].
