不同高径比时软岩强度与变形尺寸效应试验研究
2010-05-31陈瑜黄永恒曹平衣永亮李娜李丽娟
陈瑜,黄永恒,曹平,衣永亮,李娜,李丽娟
(中南大学 资源与安全工程学院,湖南 长沙,410083)
岩石是指由各种裂隙切割而形成的岩块,又称为结构体。岩石由于其生成条件及生成后数亿年的地质构造作用和大气风化作用,在岩石内部形成各种类型的空隙、微裂隙及肉眼可见的各种缺陷,它们直接影响岩石的物理力学性质,因此,不同的岩石样本的力学性质常表现出差异,即产生所谓尺寸效应[1]。软岩是一种在特定环境下具有显著塑性变形的复杂岩石力学介质,其强度低,孔隙度大,胶结程度差,受构造面切割及风化影响显著或含有大量膨胀性黏土矿物。本文所采用的实验试件均为金川二矿区的典型软岩。Hudson等[2]基于不同尺寸大理岩石的单轴压缩试验结果表明:岩石抗压强度随岩样高径比变化而变化,具有尺寸效应,但他们并没有对岩石材料尺寸与强度的定量关系以及机理进行探讨;刘宝琛等[3]对前人做过的7种岩石单轴抗压强度试验结果进行了分析,得到岩石强度随试样尺寸呈指数型衰减规律的公式;杨圣奇[4]对岩石材料的非均质性与强度尺寸效应之间的关系进行了讨论,指出岩样尺寸效应不仅体现在强度的平均值上,而且与强度的离散性相关,同时对单轴拉伸强度的尺寸效应进行了定性分析,得到岩样单轴拉伸的平均强度随尺度的增大而降低的规律;何满潮等[5]通过建立工程岩体的连续性模型,研究了工程岩体力学参数的尺寸效应;周火明等[6]采用室内和现场岩体力学试验和数值模拟等手段,对三峡永久船闸边坡岩体宏观力学参数进行了研究,建立了岩体变形模量与尺寸之间的关系;王学滨等[7]也利用剪切梯度塑性理论,建立了单轴受压下岩样尺寸效应的塑性剪切应变梯度模型。可见,岩石材料的尺寸效应现象一直是岩石力学界有待解决的问题,它直接关系到岩土工程设计、实验和数值计算时岩石力学参数的选取和预测[8-11]。在此,本文作者在伺服机上对 2组采自金川二矿区的直径相同而高度不同的岩石样本进行单轴压缩试验,研究岩石的尺寸的高径比与强度、变形特性和破裂形式等规律,并对相应的机理进行探讨。
1 矿区地质条件
金川二矿区位于大背儿泉沟出口的洪积扇顶端下部,是1个隐伏矿床。矿区地层主要为前震旦系和第四系组成,其中:前震旦系岩层由北至南,从老到新分布,岩性主要为蛇纹石化大理岩、混合岩化片麻岩及二云片麻岩等;第四系地层广泛分布于矿区中北部,往北与广阔的戈壁相连。
随着开采强度的日益加大,目前,金川矿山开采深度已超过1 km。金川二矿区矿体具有倾斜、厚大、破碎软弱、高地应力、节理裂隙发育、岩体单块强度高、整体强度低等地质特征。
2 试验系统、岩性特征和试验结果
采用的试验系统为上海新三思微机控制电液伺服刚性试验机。实验采用位移控制,荷载-位移全过程曲线由x-y函数记录仪直接绘出。选用的岩石试验样本的岩性分别为贫矿和白云石大理岩,其力学参数见表1。其中:D和H分别为岩样的直径和高度;σ0为岩样的单轴抗压强度;ε0为岩样的峰值应变(这里的应变指的是整个试样的平均应变,而不是试样中部受端部约束较小的部位的应变);E0为岩样的弹性模量,即应力-应变曲线上近似直线部分的平均斜率;E50为岩样的变形模量,即岩样峰值强度一半处对应的应力与应变的比值。
2.1 不同尺寸时岩体试件的应力-应变关系
通过试验,得到了不同尺寸时岩样试件卸荷的应力-应变关系曲线,结果如图1和图2所示。
从图1和2可以看出:岩石样本所能承受的最大应力随着试样高度的变化而变化,高度较大,最大应力值较大;高度较小,最大应力值较小;对应于试样高度分别为48.34,78.02和96.08 mm的试件,贫矿试件的曲线斜率分别为3.172,4.915和7.596;对于试样高度分别为51.24,82.66和98.52 mm的试样,白云石大理岩试件的曲线斜率分别为 2.356,3.867,5.145。可见,应力-应变关系曲线的斜率随着试件高度减小而减小;当试件高度较大时,曲线较陡,也就是试件卸荷过程中的塑性变形量较小。
2.2 变形模量和弹性模量随尺寸的变化
岩样弹性模量和变形模量与高径比的关系如图 3所示。图3表明:随高径比的增加,岩柱弹性模量和极限变形模量分别都呈增加趋势,且相关关系密切,显示出一定规律;当高径比分别约为1.04,1.67,2.00时,白云石大理岩岩样的弹性模量分别为6.17,11.07和15.12,变形模量分别为1.20,2.99,3.41;贫矿岩样的弹性模量分别为3.13,5.18和8.09;变形模量分别为0.92,1.55和2.44。2组岩样的曲线表明:高径比越小,弹性模量和极限变形越小;高径比越大,弹性模量和极限变形则相应增大。由于选用数量较少的大矿柱所能支承的顶板负荷要大于数量较多的小矿柱[2],因此,这样的矿柱设计原理合理。
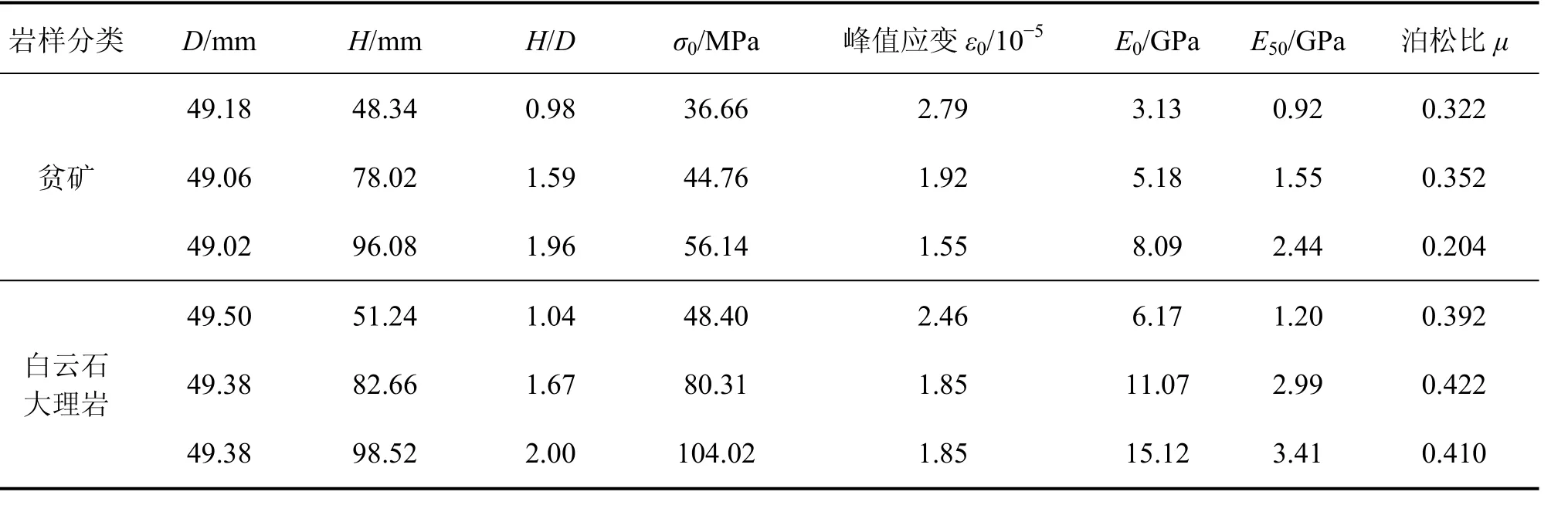
表1 岩样的力学参数Table 1 Mechanical parameters of specimens

图1 贫矿岩样试件的应力-应变关系Fig.1 Relationship between strain and stress for rock sample of lean ore
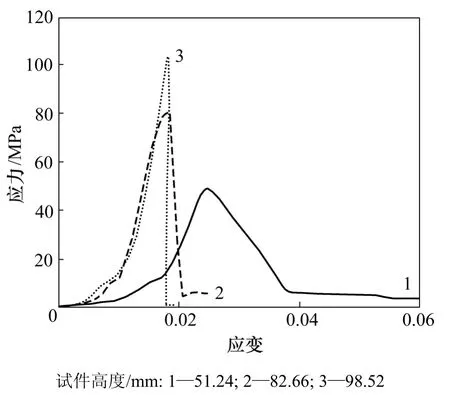
图2 白云石大理岩岩样试件的应力-应变关系Fig.2 Relationship between strain and stress for dolomite marble rock sample
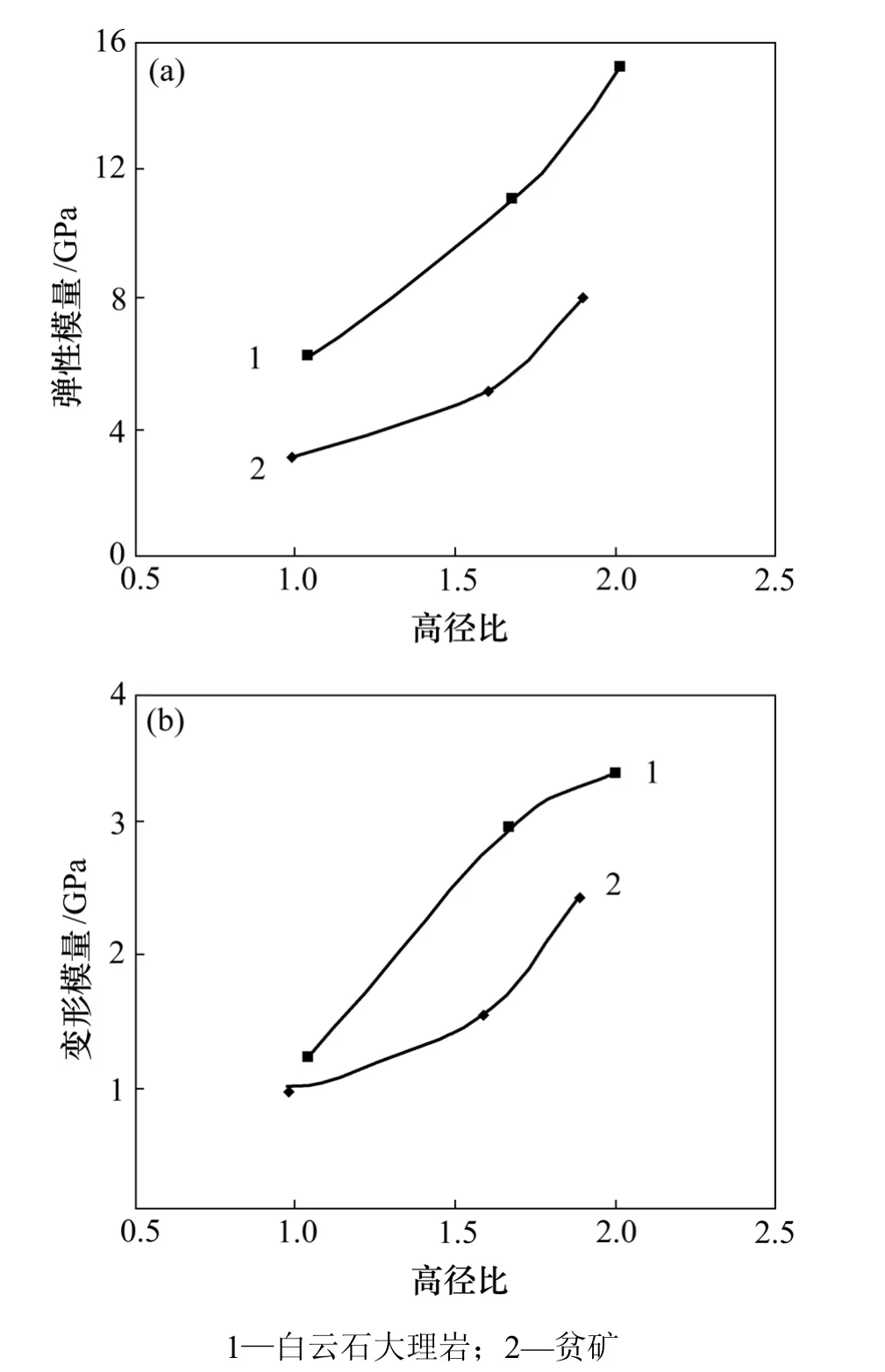
图3 岩样弹性模量、变形模量与高径比的关系Fig.3 Relationship among elastic modulus,deformation modulus of rock sample and ratio of height to diameter
3 岩样尺寸对破裂形式的影响
当岩样直径一定时,不同高度贫矿与白云石大理岩岩样的破坏形式如图4所示。
由图4可知:当高度较小时,岩样破坏形式较复杂,沿轴向出现较多的劈裂面,而高度较大时,岩样基本上呈劈裂和剪切破坏。其原因是:在单轴压缩条件下,由于上下垫板的刚度大于岩石试件的刚度,试件在压缩下的泊松比效应因试件断面与垫板间的摩擦而受到约束,因此,在试件两端形成锥形压缩区,单轴压缩时,岩样应该处于一维受压状态,从而使得岩样上下端部附近形成了三维压缩应力区(图5);高度越大的岩样中部应力区越接近一维应力状态,相反,高度越小的岩样,整体均受三维应力区的影响;当直径一定时,由于岩样端面与钢性垫块之间的摩擦作用,岩样的高度改变了其应力分布区的形式,随着高径比的减小,岩样上下端部三维压缩应力区的影响越来越大,从而使得岩样的破坏形式变得复杂[12-13]。

图4 2组岩样的破坏形式Fig.4 Failure shapes of two kinds of rock specimens
当用高径比H/D=1的圆柱形试件或高宽比为1的立方体试件时,两端的锥形压缩区必然互相连接,测得的抗压强度必然大于实际值。只有垫板的刚度与岩石刚度完全相同,才能消除端部效应的影响。但对于不同的岩石,要找到刚度相同的垫板,几乎是不可能的。国际岩石力学学会推荐用高径比为2.5~3.0的试件做抗压试验,其目的就是使试件中间部分处于单轴压缩状态,保证测出真实的单轴抗压强度。
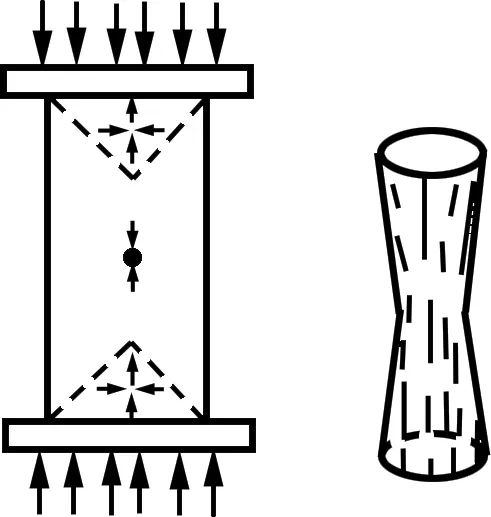
图5 单轴压缩时状态中的应力分布和破坏形式Fig.5 Stress distribution and failure mode in condition of uniaxial compressive
4 抗压强度和尺寸效应的机理
岩石强度是评价岩石工程稳定性的重要参数之一,是岩体力学研究中1个十分重要的力学指标[14-15]。研究表明:
(1) 单轴压缩下,岩石强度随着尺寸的增大而减小。龙明庆等[8]通过分析 7种岩石单轴抗压强度的试验结果,指出了强度随尺寸增加而呈幂律衰减规律。
(2) 岩石抗压强度通常是用材料内缺陷的统计分布来解释,即岩石是矿物颗粒的集合体,内部含有不同尺度的微缺陷,尺寸愈大的岩石其内部所含微缺陷的概率也愈大,因而其强度愈小。由于本文所有的岩体试件不存在肉眼可见裂隙与缺陷,因此,可对其尺寸效应乾地以下探讨。
岩体抗压强度随高径比的变化如图6所示。从图6可以看出:无论是贫矿还是白云石大理岩,当岩体高径比较小时,岩体的抗压强度较小;当岩体的高径比较大时,其抗压强度随之增大。朱珍德等[9]提出的岩石单轴抗压强度与高径比的经验公式为:
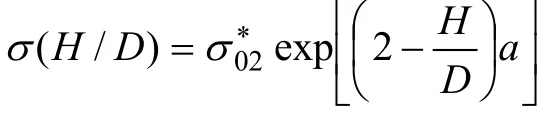
式中:σ(H/D)为任意高度H和直径D的试样的单轴抗压强度;是高径比为2时试样的单轴抗压强度;a为待定系数,与岩性和试验条件等有关,本试验中,贫矿a=-0.485,白云石大理岩a=-0.791。再对2组岩样分别进行模拟计算,得出不同高径比的单轴抗压强度如表2和表3所示。
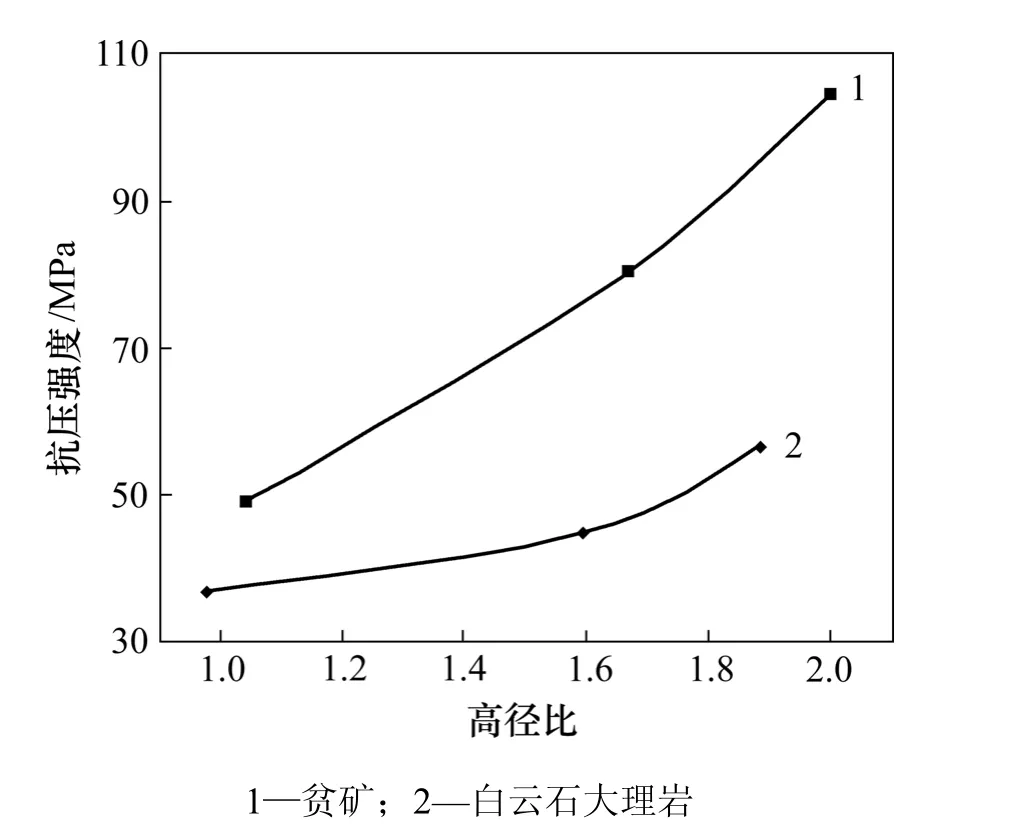
图6 2组岩样的抗压强度与高径比的关系Fig.6 Relationship between two kinds of rocks’ compressive strength and ratio of height to diameter
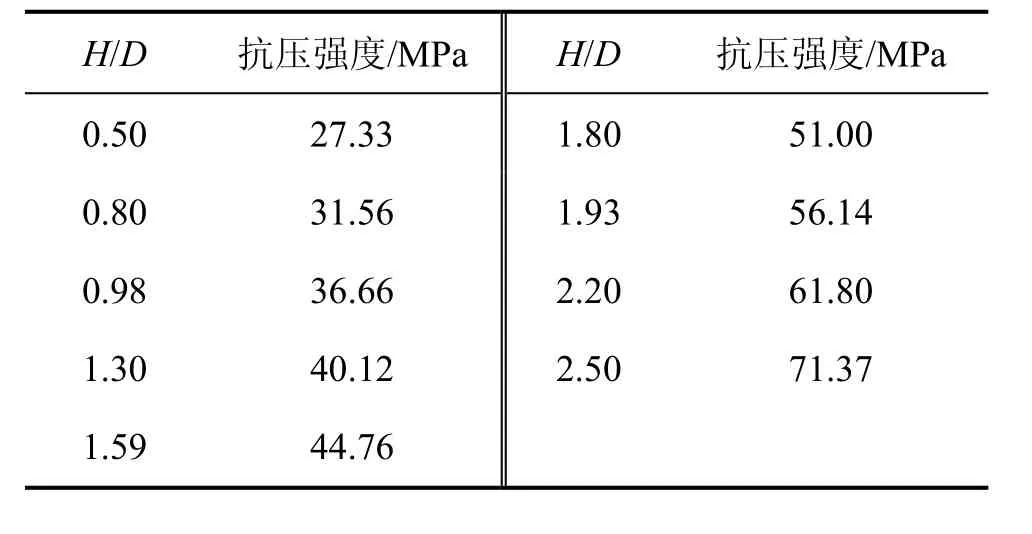
表2 不同高径比时贫矿的抗压强度Table 2 Compressive strength of lean ore with different ratios of height to diameter
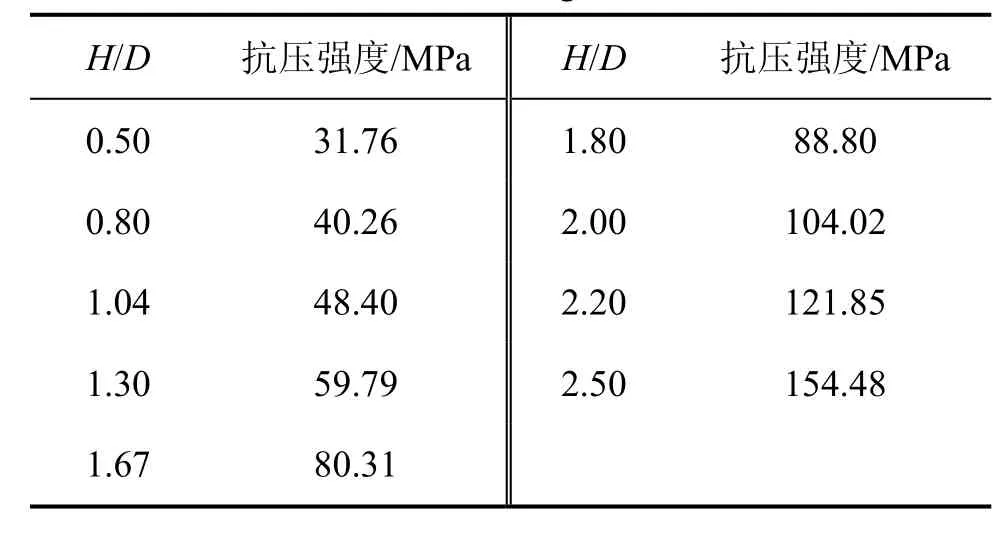
表3 不同高径比时白云石大理岩的抗压强度Table 3 Compressive strength of dolomite marble with different ratios of height to diameter
2组岩样的模拟抗压强度与高径比的关系如图 7所示。可以看出:抗压强度随岩体试件高径比增大而增大的趋势很明显,并且呈非线性规律增长。
岩石强度的尺寸效应并不是指具体2个大小不同岩样的强度差异,也不能简单地解释为岩样尺度越小则所含的缺陷越少, 因而强度增大。岩石材料变形尺寸效应是综合的平均效应[16]。这里存在2方面的因素:一方面,同直径不同高度的岩体试件,如果高度增加,岩样中微缺陷出现的概率将增加,从而导致岩石的弹性模量减小;另一方面,由于端面摩擦效应的作用,随着岩样高径比的增大,试件中间部分脱离三维压缩状态,处于单轴压缩状态,岩样内部应力分布将变得更加均匀,从而增加了岩样的弹性模量[17]。对于本文所用到的试件,由于岩样端面摩擦效应而导致内部应力分布的均匀性占据主导地位,因而其弹性模量逐渐增加。但如果微缺陷出现概率对弹性模量的影响超过端面摩擦效应的影响,则岩样的弹性模量将逐渐减小,同直径不同高度岩样的试验结果[3]验证了这一点。因此,在工程设计时,利用小尺度岩样强度的平均值作为大尺度构件内各处的强度是不合适的。这实际上假设了材料是完全均匀一致, 造成结构偏于不安全。
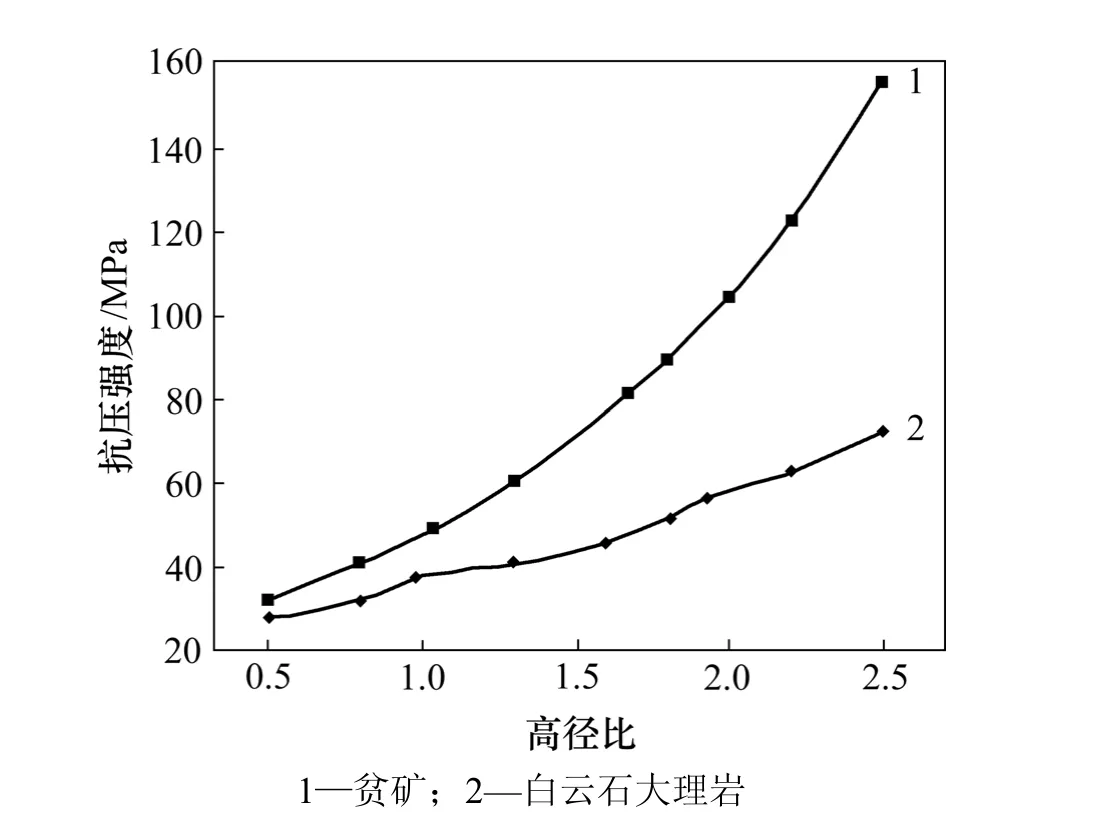
图7 2组岩样的模拟抗压强度与高径比的关系Fig.7 Relationship between simulation compressive strength and ratio of height to diameter of two kinds of rocks
5 结论
(1) 岩石应力-应变关系曲线的曲率随着高径比的增大而增大,随着高径比的减小而减小。
(2) 当岩样高径比较小时,其弹性模量和极限变形较小;当高径比较大时,其弹性模量和极限变形则相应增大。
(3) 当岩样高度较小时,岩样受到三维压缩应力区的影响,破坏形式较为复杂;高度越大的岩样中部应力区接近一维应力状态,岩石呈劈裂和剪切破坏。
(4) 岩样抗压强度随高径比的增大而增大。
(5) 尺寸效应是岩石材料本身固有特性。尽管目前对岩石强度尺寸效应的研究已取得一定进展,但由于岩石材料具有非均质性、各向异性、不连续性等特点,再加上工程岩体地质环境和条件复杂,岩石强度尺寸效应仍有待进一步研究。
[1] 王文星. 岩石力学[M]. 长沙: 中南大学出版社, 2004: 5-12.WANG Wen-xing. Rock mechanics[M]. Changsha: Central South University Press, 2004: 5-12.
[2] Hudson J A, Crouch S. Soft, stiff and servo-controlled testing machines[J]. Eng Geol, 1972, 6(3): 155-189.
[3] 刘宝琛, 张寄生, 杜奇中, 等. 岩石抗压强度的尺寸效应[J].岩石力学与工程学报, 1998, 17(6): 611-614.LIU Bao-chen, ZHANG Ji-sheng, DU Qi-zhong, et al. A study of size effect for compression strength of rock[J]. Chinese Journal of Rock Mechanics and Engineering, 1998, 17(6): 611-614.
[4] 杨圣奇. 岩石材料的非均质性与力学特性的研究[D]. 焦作:焦作工学院, 2003: 58-67.YANG Sheng-qi. The heterogeneity and mechanical properties of rock material[D]. Jiaozuo: Jiaozuo Institute of Technology,2003: 58-67.
[5] 何满潮, 薛廷河, 彭延飞. 工程岩体力学参数确定方法的研究[J]. 岩石力学与工程学报, 2001, 20(2): 225-229.HE Man-chao, XUE Ting-he, PENG Yan-fei. A new way of determining mechanical parameters of engineering rock masses[J]. Chinese Journal of Rock Mechanics and Engineering,2001, 20(2): 225-229.
[6] 周火明, 盛谦, 邬爱清. 三峡工程永久船闸边坡岩体宏观力学参数的尺寸效应研究[J]. 岩石力学与工程学报, 2001, 20(5):661-664.ZHOU Huo-ming, SHENG Qian, WU Ai-qing. Size effect analysis of macro-mechanics parameters for the rock masses of the TGP ship lock slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2001, 20(5): 661-664.
[7] 王学滨, 潘一山, 宋维源. 岩石试件尺寸效应的塑性剪切应变梯度模型[J]. 岩土工程学报, 2001, 23(6): 711-713.WANG Xue-bin, PAN Yi-shan, SONG Wei-yuan. The model of plastic shear strain grandient on size effect in uniaxial compression of rock specimens[J]. Chinese Journal of Geotechnical Engineering, 2001, 23(6): 711-713.
[8] 尤明庆, 华安增. 岩样单轴压缩的尺度效应和矿柱支承性能[J]. 煤炭学报, 1997, 22(1): 37-41.YOU Ming-qing, HUA An-zeng. The size effect of uniaxial compression of rock specimen and support capacity of ore pillar[J]. Journal of China Coal Society, 1997, 22(1): 37-41.
[9] 朱珍德, 邢福东, 王军, 等. 基于灰色理论的脆性岩石抗压强度尺寸效应试验研究[J]. 岩土力学, 2004, 25(8): 1234-1238.ZHU Zhen-de, XING Fu-dong, WANG Jun, et al. Experimental study on size effect on compression strength of brittle rock based on grey theory[J]. Rock and Soil Mechanics, 2004, 25(8):1234-1238.
[10] 李宏, 朱浮声, 王泳嘉, 等. 岩石统计细观损伤与局部弱化失稳的尺寸效应[J]. 岩石力学与工程学报, 1999, 18(1): 28-32.LI Hong, ZHU Fu-sheng, WANG Yong-jia, et al. Size effect of statistical mesoscopic damage and local weakening failure of rock[J]. Chinese Journal of Rock Mechanics and Engineering,1999, 18(1): 28-32.
[11] 杨友卿. 岩石强度的损伤力学分析[J]. 岩石力学与工程学报,1999, 18(1): 23-27.YANG You-qing. Continuum damage mechanics analysis of rock strength[J]. Chinese Journal of Rock Mechanics and Engineering, 1999, 18(1): 23-28.
[12] 王学滨, 潘一山, 盛谦, 等. 试件端面效应的变形局部化数值模拟研究[J]. 工程地质学报, 2002, 10(3): 233-236.WANG Xue-bin, PAN Yi-shan, SHENG Qian, et al. Numerical simulation on strain localization of end constraint of rock specimen[J]. Journal of Engineering Geology, 2002, 10(3):233-236.
[13] 肖庆华, 徐卫亚, 巫德斌. 岩石流变力学试验数据挖掘研究[J]. 工程地质学报, 2004, 12(2): 215-220.XIAO Qing-hua, XU Wei-ya, WU De-bin. A data mining case study for the creep test data of argillite[J]. Journal of Engineering Geology, 2004, 12(2): 215-220.
[14] 邓聚龙. 灰色系统理论的GM模型[J]. 模糊数学, 1985, 5(2):22-32.DENG Ju-long. GM model of grey systems theory[J]. Fuzzy Mathematics, 1985, 5(2): 22-32.
[15] 尤明庆, 苏承东, 杨圣奇. 岩石动静态参数间关系的研究[J].焦作工学院报, 2002, 21(6): 413-420.YOU Ming-qing, SU Cheng-dong, YANG Sheng-qi. Study on the relation between the dynamic and static parameters of rocks[J]. Journal of Jiaozuo Institute of Technology, 2002, 21(6):413-420.
[16] 杨超, 崔新民, 徐水平. 软岩应变软化数值模型的建立与研究[J]. 岩土力学, 2002, 23(6): 695-701.YANG Chao, CUI Xin-min, XU Shui-ping. Establishment and study of strain-softening numerical constitutive model for soft rock[J]. Rock and Soil Mechanics, 2002, 23(6): 695-701.
[17] 王国民. 软质粉砂岩变形与强度的试验分析[J]. 岩土力学,2000, 21(4): 340-342.WANG Guo-min. Experimental study on deformability and strength of soft siltstone[J]. Rock and Soil Mechanics, 2000,21(4): 340-342.
