基于鞍点逼近的陶瓷刀具磨损寿命可靠性分析

金雅娟 张义民 张艳林

东北大学,沈阳,110004

0 引言

金属切削过程中,刀具在切除金属的同时,其本身也逐渐被磨损,当磨损发展到一定程度时,刀具便会失去切削能力。因此,对金属切削过程的摩擦、磨损进行研究,具有重要的经济意义[1-3]。金属切削刀具的可靠性是指刀具在规定的切削条件下和规定的时间内完成规定的切削工作的能力[4],该项性能直接影响生产过程中产品的质量、工作效率及整个系统功能的正常发挥,因而是衡量切削刀具性能优劣的重要指标之一,具有重大的研究意义。樊宁等[5]提出了利用 Monte-Carlo方法同切削实验相结合的方法计算Al2 O3基陶瓷刀具磨损寿命的经典可靠度与模糊可靠度。许崇海等[6]基于模糊数学和可靠性数学的基本理论,阐述了刀具模糊可靠性的基本概念和评价方法,建立了陶瓷刀具模糊可靠性与刀具材料力学性能的关系。

鞍点逼近是作渐近分析的一个非常有用的工具,最早起源于复变函数,由Daniels[7]于1954年首先提出。它的一个很大的特点就是在小样本情况下,逼近效果依然很精确。鞍点逼近理论的重要性已体现在经济统计学中的各个方面[8-10]。文献[11-12]应用鞍点逼近技术在概率不确定性方面作了大量的研究。本文将鞍点逼近理论应用在陶瓷刀具磨损寿命可靠性分析中。

1 鞍点逼近理论

设X为随机变量,X为随机变量向量,fX(x)表示随机变量X的概率密度函数,MX(t)表示随机变量X的矩母函数,则有

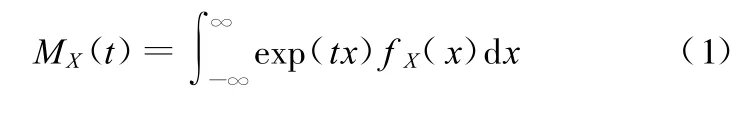
那么随机变量X的累积母函数(CGF)可由下式表示[11]：

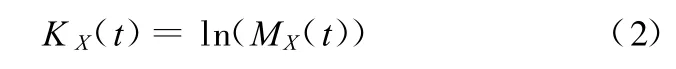
随机变量X的累积母函数有如下两个性质[11]：

(1)假设X1,X 2,…,X n为相互独立的随机变量,并且用KXi(t)(i=1,2,…,n)表示它们的累积母函数,那么的累积母函数可由下式表示：

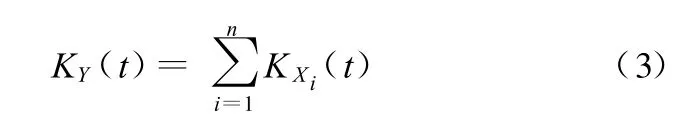
(2)假设随机变量 X的累积母函数为K X(t),那么Y=aX+b的累积母函数表示为

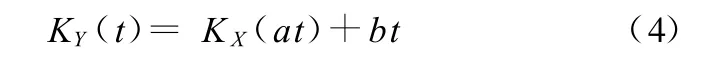
式中,a、b为常数。

极限状态方程Y=g(X)的概率密度函数(PDF)可以通过下式求得[7]：

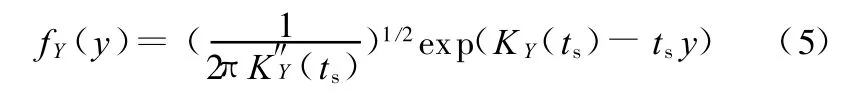
式中,KY(◦)为Y=g(X)的累积母函数;K″Y(◦)为Y=g(X)的累积母函数的二阶导数;ts为鞍点,ts的值为K′Y(t)=y 的解。

Lugannani等[13]给出了计算Y=g(X)累积分布函数(CDF)的精确公式：

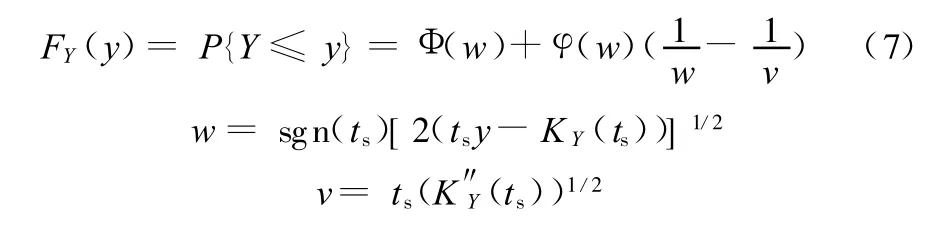
式中,Φ(◦)、φ(◦)分别表示标准正态分布函数的累积分布函数和概率密度函数。

2 陶瓷刀具磨损寿命可靠性分析

2.1 陶瓷刀具磨损寿命

陶瓷刀具的磨损机理主要有磨粒磨损、黏结磨损、化学反应与扩散磨损、氧化磨损等。对于Al2O3基陶瓷,由于其化学稳定性好,摩擦因数小,所以在几种磨损机理中,化学反应与扩散磨损的影响较小,可不考虑;黏结磨损和氧化磨损分别涉及由磨损副材料组合所决定的活化能以及材料的氧化活化能,由于活化能只是材料力学性能的隐函数,故在本文中这两种磨损机理不予考虑;而对于磨粒磨损,由于其磨损机理简单,磨损形貌清晰且较易测量,在切削用量较小的情况下,磨粒磨损所占的比例较大,因而可用磨粒磨损来衡量陶瓷刀具磨损性能的优劣[5]。对于磨粒磨损,材料的断裂韧度和硬度对材料的耐磨性有很大的影响,Evans等[14]和 Wayne等[15]证明,其磨损率w s为

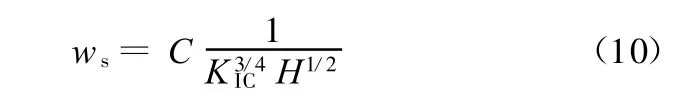
式中,KIC为断裂韧度;H为硬度;C为与摩擦条件有关的系数,由于本文主要研究不同组分系的Al2O3基复相陶瓷刀具的磨损寿命问题,而暂不考虑工件材料对刀具磨损的影响,所以在本文中C作为常数。

确定了磨钝标准M即可确定磨损体积V,根据式(10),刀具的磨损寿命N为[5]

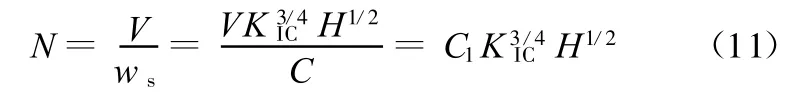
其中,C1为与切削过程有关的常数,不考虑工件材料的影响,对于不同的Al2O3基陶瓷刀具材料,只要切削过程所使用的各工艺参数一致,则C1保持不变。

2.2 基本随机参数均值与标准差的确定

以某种Al2O3基复相陶瓷刀具为例进行说明。许崇海等[16]已分别测得某种Al2O3基复相陶瓷刀具断裂韧度和硬度的若干试验值,并利用回归方法求得了两项力学性能的概率分布函数分别为三参数的Weibull分布函数：

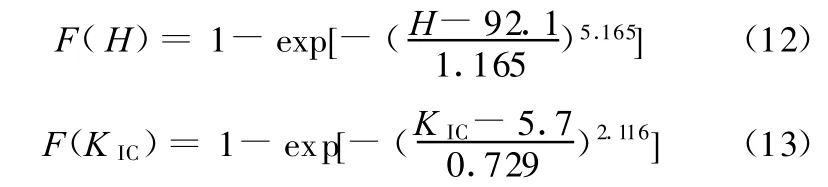
三参数Weibull分布的均值和方差分别为[17]

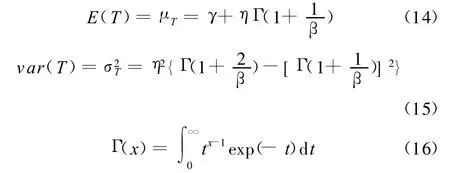
则由式(14)、式(15)可分别计算出断裂韧度K IC和硬度H的均值和标准差。

当极限状态方程中含有非正态变量时,可以用一个与原函数等效的正态分布代替,所选用的这个正态分布与原函数的等效条件是：在任一设计点处应满足分布函数值相等和概率密度函数值相等[17]。

设与原函数等效的正态分布的均值和标准差分别为μ′Xi和σ′Xi,则[17]

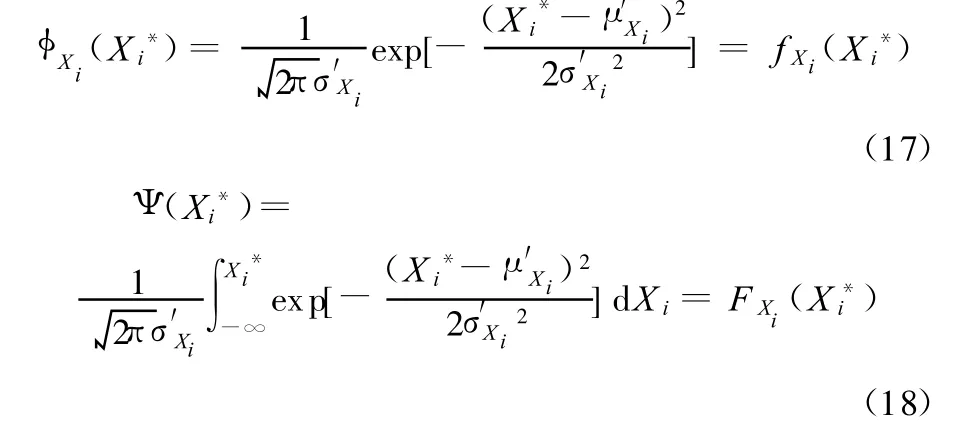
式中,fXi(◦)、FXi(◦)分别为原函数的概率密度函数及分布函数;φXi(◦)、Ψ(◦)分别为与原函数等效的正态分布的概率密度函数及分布函数。

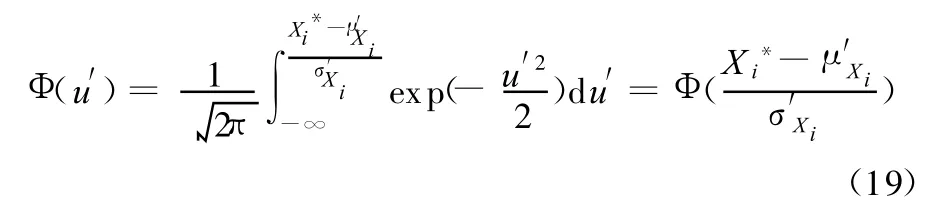
所以

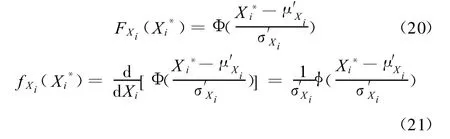
根据式(20)及式(21)可求得等效正态分布的均值和标准差为

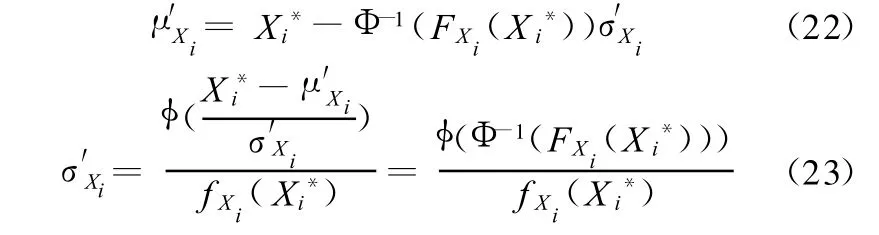
一般采用迭代法计算等效正态分布的均值和标准差,迭代数次即可收敛。

2.3 刀具磨损寿命可靠性分析模型

刀具的磨损寿命只反映刀具个体性能的优劣,不能反映刀具的可靠性问题,因此不能有效地应用于实际。刀具可靠性通常指刀具在规定的时间内、在规定的条件下,完成规定的切削工作的能力[4]。要计算刀具的磨损寿命可靠性,首先必须确定一定的标准,这个标准称为寿命阈值,通常寿命阈值是给定的。假定在一定的切削条件下,得到某种刀具的平均磨损寿命值 N1,在本文中,将平均磨损寿命 N1作为该种切削条件下的判断标准[18]。可靠性分析计算的任务就是求出刀具的寿命大于寿命阈值N1的概率,或者,给出一定的概率(可靠性要求),求解寿命阈值N 1,即

式中,R为可靠度;f(x)为磨损寿命的概率密度函数;g(X)为状态函数,可表示系统的两种状态。

为了简化求解过程,将状态方程转化为如下形式：

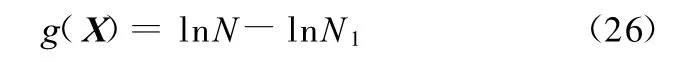
为了求出状态函数的累积母函数,首先将其作线性化处理,根据泰勒公式,在随机变量的均值处将g(X)线性展开,并取展开公式的前两项,则

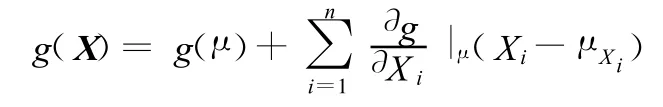
根据上述随机变量X的两个性质,以及经过泰勒展开线性化的状态函数g(X),状态函数式

(25)的累积母函数可由下式表示：

3 数值算例

根据许崇海等[19]利用回归方法求得的某种Al2O3基复相陶瓷刀具断裂韧度和硬度两项力学性能的三参数Weibull分布函数,利用本文提到的三参数Weibull分布均值和方差的求解方法得到断裂韧度K IC、硬度H的均值和标准差分别为(μKIC,σKIC)=(6.03,0.3838),(μH,σH)=(92.326,0.4767),利用等效正态分布法,经过三次迭代运算,得到等效正态分布的断裂韧度K IC和硬度 H 的均值和标准差分别为(μ′KIC,σ′KIC)=(6.3129,0.3377)和 (μ′H, μ′H)=(92.1852,0.2402)。根据樊宁等[5]提供的数据,取对数平均磨损寿命ln N1的平均值7.275为磨损寿命阈值,取ln C1为3.623。利用本文提出的鞍点逼近理论分析了陶瓷刀具的磨损寿命可靠性,并与用Monte-Carlo方法得到的结果进行了对比,结果如图1、图2所示。

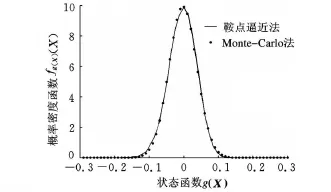
图1 概率密度函数比较曲线

在Monte-Carlo仿真计算中,根据文献[5]提供的资料,随机生成了20 000组断裂韧度K IC、硬度 H样本值,求得了 g(X)=N-N 1=C1K3/4ICH1/2-N1＞0时的概率。由图1、图2可以看出,由鞍点逼近法求得的Al2O3基陶瓷刀具的磨损寿命的状态函数的概率密度函数曲线和累积分布函数曲线与用Monte-Carlo方法求得的结果基本上一致,并且尾部拟合较好,误差很小,可靠性分析结果基本上一致。

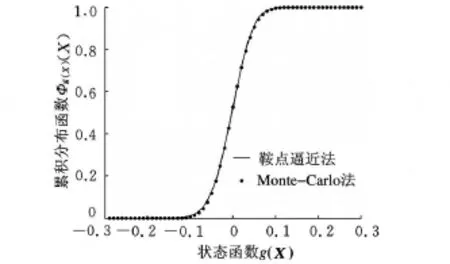
图2 累积分布函数比较曲线

4 结论

(1)利用等效正态分布法将服从Weibull分布的断裂韧度K IC和硬度 H等效正态化,进而应用鞍点逼近技术分析了Al2O3基陶瓷刀具的磨损寿命可靠性。

(2)应用鞍点逼近理论分析刀具的磨损寿命可靠性,得到状态函数的累积分布函数的同时,在没有进行累积分布函数求导的情况下,得到了状态函数的概率密度函数曲线。

(3)由于鞍点逼近理论不仅应用了随机参数的均值和标准差,并且将状态函数的完整信息也应用到了刀具磨损寿命可靠性分析中,所以得到了精度颇高的随机响应的概率密度函数和累积分布函数,这一点也通过与Monte-Carlo数值分析方法对比得到了验证。

[1] 肖茂华,何宁,李亮,等.陶瓷刀具高速切削镍基高温合金沟槽磨损实验研究[J].中国机械工程,2008,19(10)：1188-1192.

[2] 宋新玉,赵军,姜俊玲.加工Inconel718时陶瓷刀具的磨损机理[J].中国机械工程,2009,20(7)：763-767.

[3] 邵芳,刘战强,万熠,等.基于热力学的 LT55陶瓷刀具加工45钢扩散与氧化磨损[J].中国机械工程,2009,20(1)：74-78.

[4] 李兆前.金属切削刀具可靠性的研究[D].济南：山东工业大学,1993.

[5] 樊宁,艾兴,邓建新.陶瓷刀具的磨损寿命可靠性[J].机械工程学报,2002,38(4)：30-35.

[6] 许崇海,艾兴,李兆前,等.陶瓷刀具模糊可靠性及其与刀具材料力学性能的关系[J].山东工业大学学报,1998,28(6)：515-520.

[7] Daniels H E.Saddlepoint Approximations in Statistics[J].Ann.Math.Statist.,1954,25：631-50.

[8] Wang S.General Saddlepoint Approximations in the Bootstrap[J].Statist.Probab.Lett.,1992,13(1)：61-66.

[9] Reid N.Saddlepoint Methods and Statistical Inference(with discussion)[J].Statist.Sci.,1988,3：213-238.

[10] Gouits C,Casella G.Explaining the Saddle Approximation[J].Am.Statist.,1999,53(3)：216-224.

[11] Huang Beiqing,Du Xiaoping.Probabilistic Uncertainty Analysis by Mean-value First Order Saddlepoint Approximation[J].Reliability Engineering and System Safety,2008,93：325-336.

[12] Du Xiaoping.Saddlepoint Approximation for Sequential Optimization and Reliability Analysis[J].Journal of Mechanical Design,2008,130：1-11.

[13] Lugannani R,Rice S O.Saddlepoint Approximation for the Distribution of the Sum of Independent Random Variables[J].Adv.Appl.Probab.,1980,12：475-90.

[14] Evans A G,Wilshaw T R.Quasi-static Solid Particle Damage in Brittle Solids(I)：Observations A-nalysis and Implications[J].Acta Metal,1976,24(10)：939-956.

[15] Wayne S F,Buljan S T.Microstructure and Wear Resistance of Silicon Nitride Composites[M].New York：Elsevier Press,1994.

[16] 许崇海,黄传真,邓建新,等.氧化铝基陶瓷刀具切削可靠性研究—力学性能的随机特性分析[J].机械设计与制造,1996,20(6)：13-15.

[17] 张义民.汽车零部件可靠性设计[M].北京：北京理工大学出版社,2000.

[18] 樊宁,高子辉,艾兴.陶瓷刀具的破损寿命及其可靠性[J].中国机械工程,2004,15(23)：2134-2137.

[19] 许崇海,艾兴,黄传真.氧化铝基陶陶瓷刀具切削可靠性研究——基于磨损的刀具可靠性[J].工具技术,1998,32(1)：4-7.