基于微粒群算法的盲解卷积及其在故障轴承声信号中的应用

沈 沂 伍 星 迟毅林 王 宇

昆明理工大学,昆明,650093

0 引言

故障诊断技术是工业设备维护和检修的关键技术和重要手段,其中,轴承是机械设备维护的重点之一,据统计,约有30%的机械故障都是由滚动轴承引起的,滚动轴承工作状态的好坏直接影响整台机械设备的工作状态。轴承在运转过程中,若内外圈存在局部不规则损伤(如剥落、点蚀等),必然会由此产生间断性脉冲冲击激振,使所测得的声信号包含迅速衰减的脉冲响应分量。这种脉冲响应成分通常在时域上呈一定规律地出现,其发生的频率可用来准确诊断局部损伤的轴承元件。

传统的振动故障诊断技术有其局限性,所以具有非接触测量、简便易行和不需要在设备上增加附加质量而影响设备运行等特点的声学诊断法受到越来越多的关注。然而,机械声学诊断法相对于振动诊断法最大的困难在于,工业现场声场环境非常复杂,传声器接收到的观测信号往往是一个复杂的混合过程的结果[1]。因此,排除或抑制干扰和背景噪声信号,准确提取出待识别的目标信号,是进行机械设备声学故障诊断的根本。盲源分离技术为此提供了一种有效的解决方法,由于噪声传播过程中存在反射等多种因素影响,故大多数情况下噪声分析更适合采用卷积模型[2-4]。盲解卷积技术的研究虽然起步较晚,但近年来发展迅速,已有相关应用研究。

1 盲解卷积数学模型

在卷积混合中,m个接收信号组成一个m维的接收信号向量 x(k)=(x1(k),x2(k),…,xm(k))T,同样,n个源信号组成源信号向量s(k),s(k)=(s1(k),s2(k),…,sn(k))T,n ≤m,其中,k为信号的长度,x(k)是由s(k)经过一个线性卷积混合模型后得到的混合信号,用数学表达式写为

式中,Hp为延迟为p时的混合滤波器矩阵;hij为从第j个源信号到第i个传感器之间的冲激响应。

由于si(k)和sj(k)(i≠j)是由两个不同的信号源发出的,因此通常假设它们是相互独立的。

当混合信号向量x(k)通过一组线性分离滤波器W后,可以得到对源信号向量s(k)的估计向量y(k),其数学表达式可写为

式中,Wp为计算出的延迟为p的分离滤波器矩阵。

时域算法就是基于上述原理,通过找到一个合适的代价函数C、约束函数和迭代学习方法来找到最优分离滤波器,从而分离出原始信号。

2010年开展的“青海库郎米其—布伦台地区1∶25万区域化探”采样截取粒级为-10～+60目，平均采样密度为2.97个点/4km2；针对残山景观区水系极不发育且风成物严重干扰情况下，用有效控制汇水域的思想，多点组合采集岩屑样代替水系沉积物样。

本文选用盲抽取方法来分离信号,其优点如下：可按照源信号的特征以特定的顺序进行抽取;抽取方法灵活;可仅仅抽取感兴趣的少数源信号,缩短了计算时间;抽取算法通常比同时分离算法简单。典型的抽取算法包括抽取和压缩两个步骤。

所用的时域盲解卷积算法的基本流程如下：

(1)抽取步骤。找到一个1×m维的滤波器矩阵g,按下式分离出第一个估计信号：

式中,r(k)为本次抽取所得的第1个估计信号。

(2)压缩步骤。对每一个估计信号r(k),找到对应的m×1维滤波器t,将分离出的信号从原有混合信号中剔除,得到新的混合信号,再进行下一步迭代,数学模型如下：

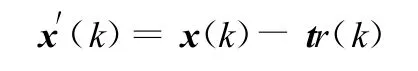
同理,此时再定义一个代价函数,通过找到其最大值来确定最优的 t◦g,从而剔除估计信号[7]。

与其他盲解卷积算法类似,对于不同的观察信号,需选用不用的代价函数,才能达到预期的分离效果。

2 微粒群算法

微粒群算法的主要思想是,用同伴的飞行经验来调整自身的速度和位置。粒子自身的飞行经验指该粒子找到的最优解,称为个体极值;同伴的飞行经验指该粒子周围其他粒子目前找到的最优解,称为群体极值。当把整个种群定义为同伴时,算法称为全局版微粒群算法;当同伴仅指种群中的一部分粒子时,算法称为局部版微粒群算法。全局版微粒群算法收敛速度快,但可能陷入局部最小点;局部版微粒群算法收敛速度慢,但极少陷入局部最小点。

算法的基本流程如下：①初始化一群微粒(群体规模为m),包括随机位置和速度;②评价每个微粒的适应度;③对每个微粒,将其适应值与其经历过的最好位置p best作比较,如果新位置的适应值大,则将其作为当前的最好位置pbest;④对每个微粒,将其适应值与全局所经历的最好位置g best作比较,如果新位置的适应值大,则重新设置gbest的索引号;⑤根据下式变化微粒的速度vij(t)和位置xij(t)：

式中,w为惯性权重;c1、c2为学习因子;p(t)为t时刻粒子的位置。

⑥如未达到结束条件(通常为设定的适应度值或达到一个预设最大代数G max),则返回 ②。

3 基于微粒群算法的盲解卷积改进方法

目前的时域盲解卷积算法普遍存在无法准确估计分离滤波器长度的缺点,相比遍历算法及运用比较广泛的遗传算法,微粒群算法基于自身的优点更适合用来确定传统盲解卷积算法中的分离滤波器长度L。

基于微粒群的盲解卷积算法的主要步骤如下：①对混合信号采样并中心化或预白化。②初始化粒子种群,以分离滤波器长度作为粒子,随机产生一定数量的、以分离滤波器长度作为粒子的初始位置,随机初始化每个粒子的移动速度。③根据粒子的位置(即分离滤波器的长度)分离信号,并计算每个粒子的适应度。一个实值为零、均值为随机变量y的峭度定义为

式中,E(y4)为y的四阶矩。

峭度统计量对信号的峰值陡变非常敏感,它还常用来检测信号中脉冲成分的出现或幅值变化,也是机械故障振动信号监测的常用指标。因此,分离轴承故障信号时,适应度选为峭度最大值的倒数。④根据粒子的适应度更新各粒子的位置和速度。⑤更新各粒子的位置和速度。⑥进入循环,转至第 ③步,迭代到预设的迭代步数或设定的适应度时,输出最优解。

4 计算机仿真

为模拟实际信号,在MATLAB中生成周期脉冲衰减信号s1(t)以模拟轴承故障信号,生成正弦信号s2(t)以模拟机械的周期信号,生成白噪声信号s3(t)以模拟环境噪声,白噪声信号的幅值三倍于正弦信号和周期脉冲衰减信号,这三个信号的公式如下：

时域波形图见图1,与三个信号经人工卷积混合后,混合信号如图2所示,可见,冲击信号完全淹没在噪声中。其中混合滤波器长度选为3,混合矩阵中的元素为随机数。卷积混合公式如下：

图1 模拟信号时域波形图

图2 混合信号时域波形图

用上述改进方法并结合Simon[7]提出的时域盲解卷积算法进行信号分离。由于微粒群优化的搜索空间维数为1,所以学习因子c1、c2和惯性权重w对收敛速度影响不大,而最大迭代次数、起止范围、初始化群体个体数目和收敛精度对收敛速度影响较大。最大迭代次数设置得越大,收敛精度设置得越小,计算的时间就越长;初始化群体个体数目越大,计算速度就越快;由于该时域盲解卷积算法本身存在解长卷积信号困难的问题,终止数(即分离滤波器长度的最大值)不宜取太大,而初始值取1即可。实际使用时,最大迭代次数选终止数的1/3,一般就能保证算法准确收敛;收敛精度应根据适应度来定;初始化群体个体数目取终止数除最大迭代次数的近似整数。仿真中单个分离信号数据点数为1281,取c1=c2=1.5,w=0.8,最大迭代次数为10,初始化群体个体数目为3,收敛精度为0.1,终止数为30,这样可在2min内完成数据的分离。以峭度最大值的倒数为微粒群算法的适应度时,s1(t)、s2(t)、s3(t)三个混合信号的分离信号如图3所示。当适应度选平均的通道互扰(inter channel interference,ICI)和码间串扰(inter symbol interference,ISI)的综合指标JMC-ISI(W)时,分离信号如图4所示。综合指标JMC-ISI(W)的计算公式如下：

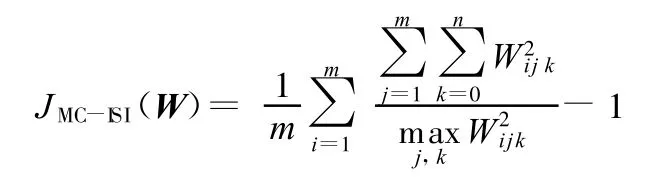
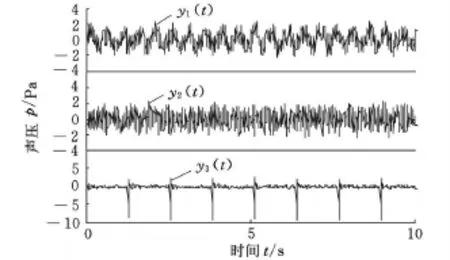
图3 基于峭度最大值倒数的分离信号时域波形图

图4 基于 ICI、ISI综合指标的分离信号时域波形图

ICI反映了多通道盲解卷积算法的信号分离效果,但不能衡量其解卷积效果,而ISI则可反映解卷积的效果,两者结合有利于评价盲解卷积效果[8]。两种适应度的改进方法都能从高噪声环境中分离冲击和周期成分。当改进方法中的适应度为峭度最大值的倒数时,改进的方法对冲击非常敏感,虽也能分离出周期信号,但效果不如适应度为综合指标J MC-ISI(W)时理想,后者分离效果较好,但对冲击的敏感性低于前者,在实际环境中提取故障冲击信号的能力不如前者,因此,分离轴承故障信号时选峭度最大值倒数为适应度较好。

仅用Simon提出的时域盲解卷积算法分离混合信号,经反复仿真验证,选择其中分离效果较好的周期平稳分离方法,且人为设定分离滤波器长度为6,得到的分离结果如图5、图6所示,可见,周期信号与冲击信号均不明显,分离效果不是很好。对比图3、图4,可见改进算法的优越性。

图5 基于原盲解卷积的分离信号时域波形图

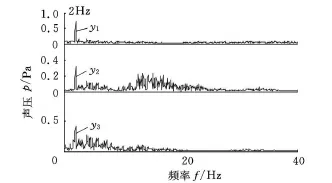
图6 基于原盲解卷积的分离信号频谱图

5 实验分析

根据上述仿真结果,分析故障轴承声信号时,选用峭度最大值倒数为微粒群算法的搜索适应度。下面基于改进算法进行实验,过程如下：实际环境中,在旋转机械振动及故障模拟实验台上仿真得到有负载且转速800r/min的外圈轴承故障声信号,用传声器来测量信号,采样频率为10k Hz。实验的滚动轴承型号为NU205,节圆直径D=39mm,滚动体直径d=7.5mm,滚动体个数z=12,接触角 α=0°,外圈故障如图 7 所示,理论外滚道故障频率为64.6Hz。3个传声器并列安放,其离地高度为0.5m,测点位置如图8所示。经多次验证,盲解卷积算法还是选用Simon提出的周期平稳分离方法效果较好,分离出的故障信号时域波形图见图9。由于第二个信号冲击比较明显且有规律,有可能就是故障信号,因此,对分离出的第二个信号作包络分析,如图10所示,读出的故障频率与理论外圈故障频率基本相符,即可证明此轴承存在外圈故障,同时验证了改进算法在声学故障诊断中的可行性。

图7 外圈故障

图8 测点位置图

图9 分离出的外圈故障信号

图10 外圈故障信号y2的包络信号图

6 结论

将微粒群算法应用到盲解卷积中,通过选择恰当的适应度找到最优的分离滤波器长度,使得分离效果最优。目前来看,选取一个适应度来分离所有信号,结果不理想,应针对不同信号选取相对应的特征量或特征函数。峭度指标是量纲一参数,它与轴承转速、尺寸、载荷等无关,对冲击信号特别敏感,适用于表面损伤类故障的诊断,因此峭度适合作为本文改进算法的适应度,实验证明,采用峭度作为适应度,分离出的信号能为进一步的诊断分析提供依据。但由于盲解卷积算法自身存在的解长卷积问题的困难,本文提出的改进算法也只是对短分离滤波器长度的盲解卷积问题(即传声器与待检测轴承距离较近)有令人满意的效果,至于如何解决长卷积问题还有待进一步研究。

[1] 宋晓萍.旋转机械振动信号的分离[D].西安：西北工业大学,2007.

[2] Eringen A C.Nonlocal Micropolar Field Theory in Contimuum Physics[M].New York：Acadamic Press,1976.

[3] Eringen A C.Line Crack Subjected to Shear[J].International Journal of Fracture,1978,14：367-369.

[4] Eringen A C.Line Crack Subjected to Anti-plane Shear[J].Engineering of Fracture,1979,12(3)：211-219.

[5] Sun X,Douglas SC.A Natural Gradient Convolutive Blind Source Separation Algorithm for Speech Mixtures[C]//IEEE International Conference on Acoustics 2001.San,Diego,California,2001：59-63.

[6] 黄之初.滚动轴承故障脉冲信号提取及诊断：一种盲解卷积方法[J].振动与冲击,2006,25(3)：150-154.

[7] Simon C.Fast Communication Separation of a Class of Convolutive Mixtures：a Contrast Function Approach[J].Signal Processing,2001,81(4)：884-887.

[8] 陈少林.声学故障诊断中信号盲处理和可视化声源识别的研究[D].上海：上海交通大学,2004.