沟槽对O形圈密封结构性能的影响

高九阳,喻九阳,王成刚,汪 威,林 纬,张 捷

(武汉工程大学机电工程学院,湖北 武汉 430074 )

0 引 言

在工业生产中，设备制造商和最终用户都希望密封系统能够无泄漏的运行，并且具有较长的使用寿命，因此设备密封性能的好坏至关重要.O形密封圈的使用范围及安装方法均有相应的国家标准，且在对其理论分析的方面已取得了相关的成果[1-8]，但并不全面.本文利用有限元方法对O形橡胶圈密封结构进行建模计算，分析了不同沟槽形式对密封性能的影响及其适用范围，为同类密封结构设计提供参考.

1 有限元模型的建立

1.1 计算模型

O形圈靠压缩后产生的回弹力给密封接触面一定压力，进而达到密封目的.密封结构中橡胶材料在受力下的位移和变形关系已远远超出了线性理论的范畴，属于几何非线性，且橡胶材料被认为是超弹性不可压缩体，因此其计算模型表现为复杂的材料非线性和几何非线性[1-3].

对于超弹性不可压缩体，基于统计热力学，已有学者提出了Heo-Hookean应变能函数模型，基于连续体的表现学，已有学者提出了Mooney-Rivlin模型、Klosenr-segal模型和Ogden-Tschoegl模型.本文的有限元计算中，O形圈的力学计算模型采用广泛用于描述橡胶材料的应变能函数——Mooney-Rivlin模型[1-2].其应变能密度函数模型如下：

式中Cij,N,dk为Mooney常数，由材料实验所确定，对于不可压缩材料J=1，典型的二项三阶展开表达式为：

本文采用此简化的应变函数模型，穆尼常数分别取为：C10=1.87，C01=0.47.

1.2 几何模型

本文所选O形圈尺寸为：31.5×2.65 mm，材料为NBR，泊松比取0.499，弹性模量为10 MPa.O形圈安装于两种常用的密封沟槽内，其平面轴对称几何模型及尺寸如图1、2所示.

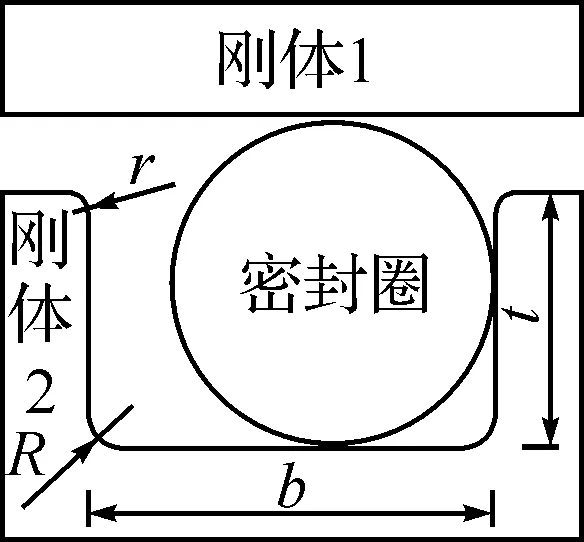
图1 矩形沟槽

图2 V形沟槽

图1中槽宽b=3.6 mm，槽深t=2.15 mm，沟槽倒角处半径为R=0.3 mm，r=0.2 mm，图2中沟槽截面最大宽度W=5.2 mm，沟槽截面夹角为90°，底部倒角半径R=0.6 mm[6].

1.3 有限元实体模型

进行有限元分析时，为了简化计算，可将O形圈密封结构简化为二维轴对称模型，通过平面模型来模拟三维结构.如图(3)所示，实体模型中，相比于刚体1及刚体2的材料，可认为只有O形圈产生变形，因此可认为刚体1及刚体2为O形圈变形时的约束边界，O形圈受到的初始压缩量即可视为由刚体1约束边界指定的位移引起[7].求解时定义刚体1一个Y=-0.25 mm的位移，使O形圈达到“安装”状态，在此基础上进一步在密封流体介质作用的一侧逐渐施加压力，模拟密封结构的实际工况.

图3 O形圈分别安装在矩形、V形沟槽内的二维轴对称计算模型

2 计算结果及分析

O形圈依靠其本身的变形产生回弹力，在与刚体接触面间产生较大的接触应力，若其峰值大于所密封介质的压力，且O形圈本身未被破坏，则能达到密封的效果[7].

2.1 密封面间最大接触应力

图4 流体介质压力与接触应力峰值的关系曲线

接触应力的大小反映了密封结构的密封能力，图4为密封流体介质压力与密封面间最大接触应力的关系曲线.随着流体压力值的增加，密封结构中接触应力峰值亦同时增加，不同流体压力作用下，矩形沟槽及V形沟槽密封结构的最大接触应力始终大于密封流体压力，均满足密封的要求；相同压缩率条件下，O形圈安装在V形沟槽内密封能力较矩形沟槽内要好.

2.2 Von Mises应力

Von Mises应力表达式为：σ={[(σ1-σ2)2+(σ2-σ3)2+(σ3-σ1)2]/2}1/2，其中σ1，σ2，σ3为材料单元体三个方向上的主应力，Von Mises应力反映O形圈材料截面上主应力差值的大小.对于应力值大的地方，材料越容易出现裂纹；此外，应力值越大，材料的形状改变比能越大，当超过一定限度时，O形圈就可能被挤入密封间隙内，被挤入的部分在拉伸和剪切的作用下其表面容易产生切割作用而被咬伤；同时，应力大将加速密封圈橡胶材料的松弛，造成“刚度”下降.为了保证O形密封圈的使用寿命，在满足密封的条件下，应优先选择应力小的密封结构.图5和图6分别为“安装”状态下和“安装”后在有密封介质作用的一侧施加3.5 MPa分布载荷情况下O形圈的Von Mises应力分布云图.

图5 初始安装状态下V形及矩形沟槽内O形圈Von Mises应力云图

图6 3.5MPa流体介质压力作用的条件下V形及矩形沟槽内O形圈Von Mises应力云图

由图5和图6可知，随着密封流体介质压力的增大，矩形及V形沟槽内O形圈Von Mises应力峰区的位置都发生了变化，且区域面积都增大，因此O形圈可能发生裂纹的位置也随之增多.表1为不同流体压力作用下矩形及V形沟槽内O形圈Von Mises应力峰值的变化情况.

表1 不同流体压力作用下O形圈Von Mises应力峰值变化情况

由表1可知，随着密封流体介质压力的增加，矩形及V形沟槽内O形圈Von Mises应力峰值都相应增大；同时，由于O形圈变形的增加，流体介质压力作用的面积减少，导致Von Mises应力峰值的增幅随着流体压力的增加而减小；相同压缩率、流体介质压力作用下，V形沟槽内O形密封圈Von Mises应力峰值始终大于矩形沟槽内应力峰值，且两者差值随着流体压力的增大而增大.

3 结 语

a. 在不同密封流体压力的作用下，V形及矩形沟槽密封结构密封面间的最大接触应力均大于密封流体压力，均满足密封要求；相同压缩率、流体介质压力条件下，V形沟槽结构密封能力要好于矩形沟槽密封结构.

b. 相同压缩率、流体压力条件下，V形沟槽结构中O形圈Von Mises应力峰值始终大于矩形沟槽内O形圈的应力峰值；且两者差值随着流体压力的增加而增加，安装在V形沟槽内的O形圈较矩形沟槽内易被破坏.

综上所述，V形沟槽仅适用于密封流体介质压力不大的情况；在密封流体介质压力较大时，矩形沟槽具有较大优势，验证了多年使用的经验设计.

参考文献：

[1]喻九阳,高九阳，王成刚，等.机械振打器活塞杆处O形圈不同密封结构下的性能分析[J].润滑与密封,2010,35(3):65-68.

[2]陈国定，Haiser H，Haas W,等.O形密封圈的有限元力学分析[J].机械科学与技术，2000，19(5)：740-742.

[3]卢霞，喻九阳,王仕仙，等.真空电阻凸焊温度场有限元分析[J].武汉工程大学学报,2009,31(5):72-76.

[4]汪威,喻九阳，杨侠，等.波节管脉冲流强化对流换热数值分析[J].武汉工程大学学报,2010,32(3):89-91.

[5]王仕仙，徐建生，卢霞，等.基于ANSYS的滑动摩擦热结构耦合分析[J].武汉工程大学学报，2009,31(5):67-70.

[6]近森德重(日).密封元件—O形密封圈[M].北京：机械工业出版社，1976：74-83.

[7]任全彬，蔡体敏，王荣桥,等.橡胶O形密封圈结构参数和失效准则研究[J].固体火箭技术，2006，29(1):9-14.

[8]孙庆新，陈旭勇，杨冬波.刚构连续弯板桥空间有限元分析[J].武汉工程大学学报,2009,31(5):41-44.