基于有限元分析的下排渣门设计

魏化中,张志辉，帅 健，杜喆恕

(1.武汉市压力容器压力管道安全工程研究中心，湖北 武汉 430074；2.武汉工程大学机电工程学院，湖北 武汉 430074；3.中国石油大学(北京)机电工程学院，北京 102249；4.武汉制药机械有限责任公司，湖北 武汉 430065)

0 引 言

中药提取罐是中药生产的关键设备，属于一类压力容器[1-3]，其下排渣门结构如图1所示.下排渣门与罐体的安全性能与密封性能是关系到提取罐能否安全生产的关键因素，下排渣门主要出现的问题是泄漏和脱钩现象，调查表明，约有80%的泄漏失效是由于下排渣门密封出现问题引起的.随着生产的大型化发展，提取罐直径的增大更有助于提高生产效率，许多中药企业需要排渣门直径进一步增大以满足生产要求.目前，国内生产的提取罐的最大直径为1.4 m，工作压力约为0.20 MPa.

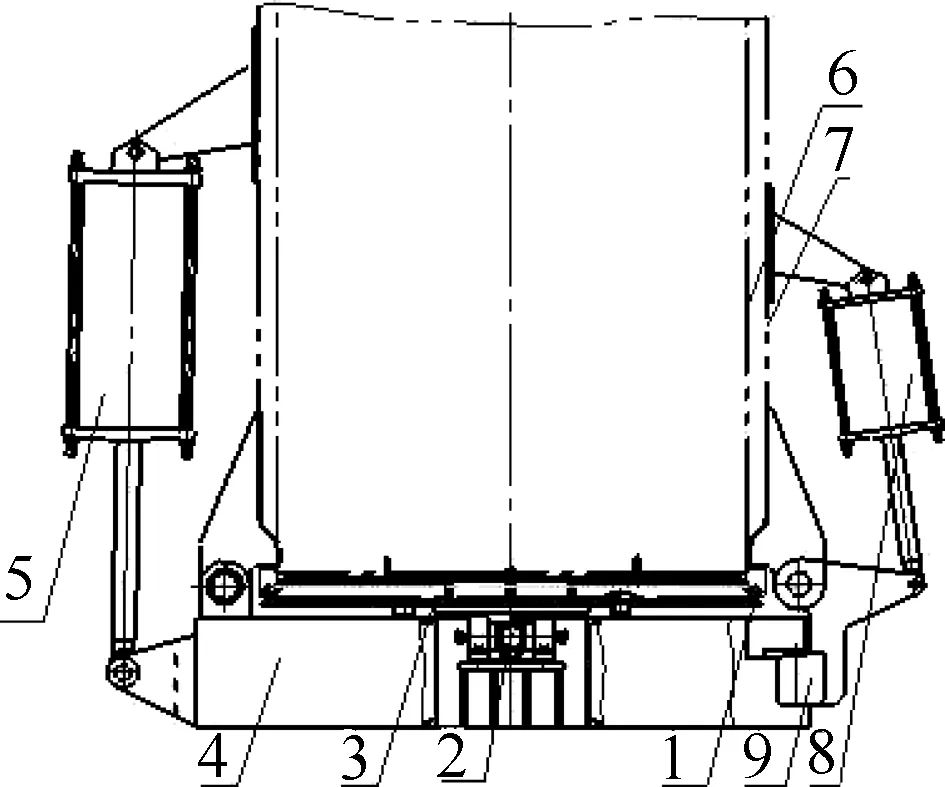
图1 下排渣门结构示意图

注：1——O型密封圈；2——十字轴；3——门盖；4——横梁；5——开盖气缸；6——罐体；7——夹套；8——锁紧气缸；9——搭钩.

大口径排渣门的设计，在满足强度、刚度以及结构紧凑运动自如等要求时，还要解决密封问题(排渣门密封结构见图2)，密封是否良好与门的变形量Δy1和横梁的变形量Δy2的总和有直接关系，当总变形量大于O形密封圈回弹量Δ，即Δy1+Δy2>Δ时，就会发生泄漏失效.门、横梁以及其它部件如十字轴和搭钩等结构都比较复杂，传统设计方法不能精确计算出它们的变形和应力情况，因此本文采用有限元方法，设计压力取0.20 MPa，计算压力取水压实验压力0.25 MPa，用ANSYS软件对横梁和门进行了计算分析和设计[4-5].

图2 下排渣门密封结构示意图

1 Φ1400 mm排渣门结构设计思路

排渣门和罐体的密封形式是自紧式密封，密封圈采用由硅橡胶制成的O形密封圈，它具有无毒无味、耐高温和耐腐蚀等特点.

生产中，排渣门的失效形式主要是发生泄漏，这往往是由于门盖和横梁的变形量超过密封圈回弹量造成的，密封圈回弹量一般在4～6 mm之间，通过实验测量，得到当门盖和横梁的变形量总和大于4 mm时就会发生泄漏，因此在设计Φ1 400 mm排渣门时首先考虑刚度，同时保证其强度，排渣门总变形量Δy1+Δy2<4 mm就能满足密封要求.

2 基于有限元法的Φ1 400 mm排渣门设计

2.1 横梁结构有限元计算分析

横梁是由槽钢和钢板焊接而成的组合梁(沿轴纵向平面对称)，它在空间三个方向具有相同量级的尺度，属于短粗梁，基于材料力学的传统设计方法已不能精确计算出横梁的变形和应力.而有限元方法能有效的解决这一问题[6].

直径为1 400 mm排渣门的横梁所承受的最大载荷达到385 kN，在对横梁结构进行预设计后，用ANSYS软件按以下几个步骤对横梁进行分析和计算：a、简化有限元计算模型；b、网格划分；c、载荷与边界条件施加；d、计算结果及其分析说明.划分网格后横梁模型(1/2模型)如图3所示.

通过对实际结构的分析，可把横梁简化为一个简支梁：一边是固定铰支座(图3左边界)，一边是活动铰支座(图3右边界).由于横梁结构和载荷均对轴纵向平面具有对称性，有限元分析时，为了减小计算规模，只需建立1/2模型进行计算.单元采用的是8节点六面体单元solid45，solid45用于仿真三维实体结构.为保证计算精度，对结构进行映射网格划分，并且把横梁中间部分网格细划，整个模型单元数为18 710，节点数为31 387，施加相应的边界条件后对其进行计算.

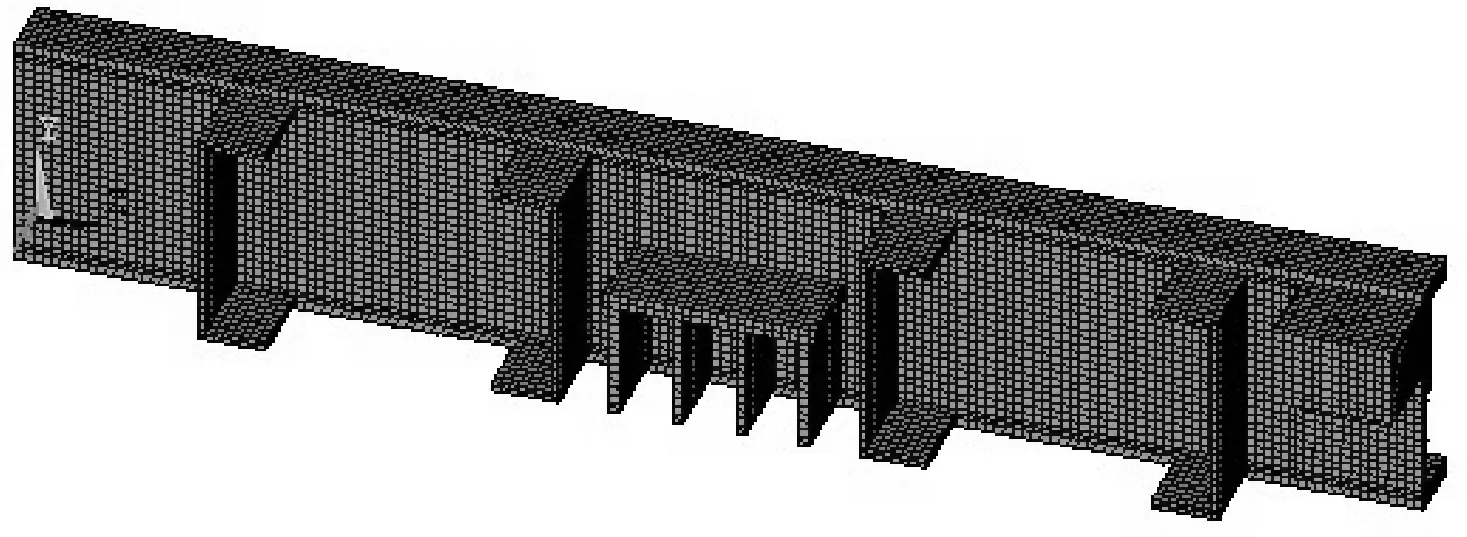
图3 划分网格后横梁有限元模型

横梁的变形计算结果如图4所示，可以看出横梁中心最大变形量达到Δy=0.766 mm，横梁中心最大变形处应力为σ=85.99 MPa，小于材料许用应力[σ]=167 MPa，满足强度要求.

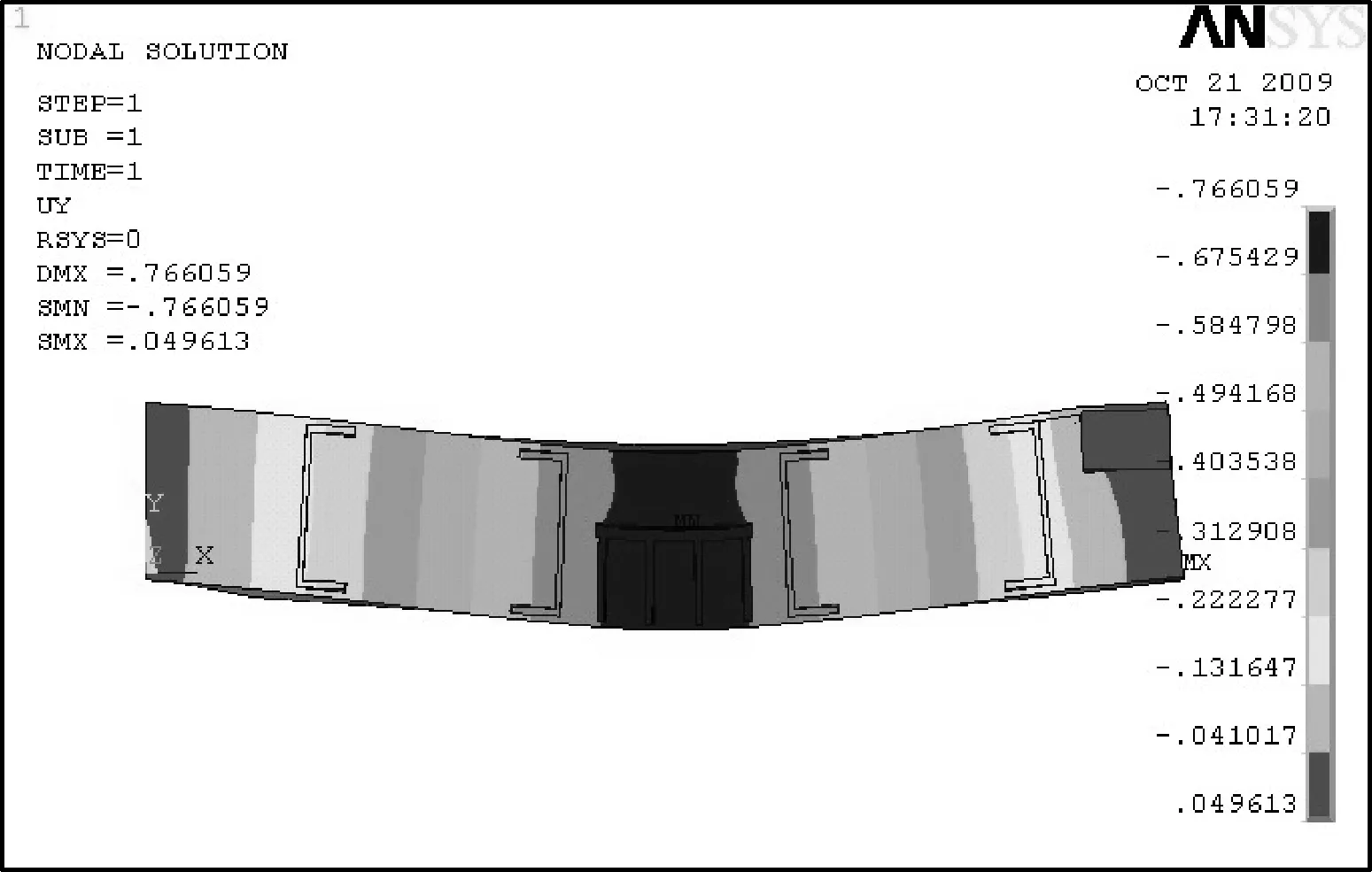
图4 横梁Y方向变形图

2.2 Φ1 400 mm门的有限元计算分析

经多次优化和计算，最终所设计门的结构如图5和图6所示，图5和图6分别是Φ1 400 mm门的整体有限元模型和剖开以后的有限元模型(除去上平板).它主要由上下两块平板、12个加强筋板、锥形圈以及连接板组合而成，由于门盖结构复杂，应用弹性理论很难求得精确的数值解，只能通过适当的假设和近似才能得到弹性理论分析的近似结果，而且计算过程过于复杂.应用有限元法可以有效地解决这一复杂问题，使工作量大大减少，而且结果精度更高[7].

用ANSYS软件，按以下几个步骤对门进行分析：a、简化模型；b、网格划分；c、载荷与边界条件施加；d、计算结果及其分析说明.为了保证计算精度，单元选取三维solid45体单元，对结构进行映射网格划分，整个模型单元数为42 498，节点数为79 587，门上施加0.25 MPa的均布压力，在对连接板上施加相应位移约束后进行计算.

图5 Φ1 400 mm门的整体有限元模型

图6 剖开后Φ1 400 mm门的有限元模型

图7 Φ1400 mm门盖Von mises 应力云图

图7和图8分别为计算完成后Φ1 400 mm门的Von mises 等效应力云图和Y向变形云图，可以得出最大变形量为1.258 mm，筋板上最大应力达到137 MPa，对危险截面按照JB4732-1995《钢制压力容器—分析设计标准》[7]进行应力评定满足要求.

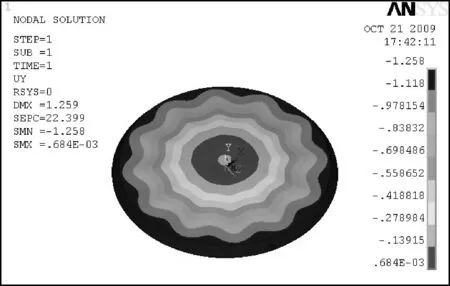
图8 Φ1 400 mm门盖Y方向变形云图

3 水压试验结果同有限元结果对比

对所设计新结构排渣门提取罐做水压试验，并在排渣门下面布置两个千分表分别用来测量横梁和门的变形量，当水压实验压力升到0.25 MPa后，保压一小时，整个提取罐密封良好满足要求，测出了在此压力下横梁和门的变形量，其结果同有限元计算结果对比如表1所示，通过对比可以看出，有限元结果小于水压试验结果，这是由于在工作时排渣门其它部件如十字轴和搭钩都会产生一定量的变形造成的，它们的变形量都很小，对结果影响不大.总体来说有限元计算结果与水压试验测试结果比较吻合，有限元方法可以较准确地模拟横梁和门的真实变形和应力分布情况，说明有限元模型是合理的.

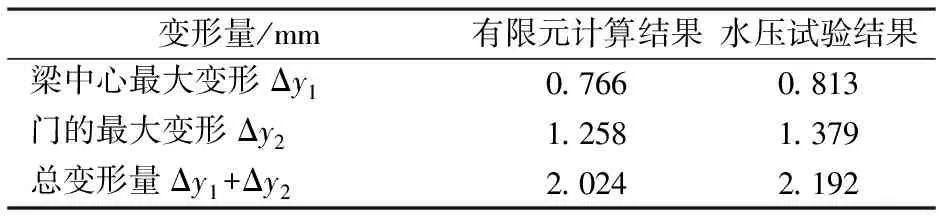
表1 水压试验结果和有限元计算结果对比

4 结 语

a.有限元方法应用于中药提取罐下排渣门复杂部件的结构设计之中，可以准确地模拟复杂形体部件的变形和应力状态，进而对其优化设计作出指导.

b.本文设计方法对中药提取罐大口径排渣门的设计具有一定的参考价值.

参考文献：

[1]郑津洋,董其伍,桑芝富.过程设备设计[M].北京:化学工业出版社,2005:12-15

[2]郑津洋.快速开关盖式压力容器(一)[J].化工装备技术,1997,18(1):30-38.

[3]张红卫，陈刚，刘岑，等.标准椭圆封头对薄壁内压圆筒承载能力的影响[J].武汉工程大学学报，2010，32(3)：103-106.

[4]余伟炜,高炳军.ANSYS在机械与化工装备中的应用[M].北京:中国水利水电出版社,2006.

[5]王仕仙,徐建生,卢霞.基于ANSYS的滑动摩擦热结构耦合分析[J].武汉工程大学学报,2009,31(5):67-71.

[6]孙庆新,陈旭勇,杨冬波.钢构连续弯板桥空间有限元分析[J].武汉工程大学学报,2009,31(5):41-43.

[7]JB4732-1995,钢制压力容器—分析设计标准[S].