一类具有球面叶层结构的二次广义Hamilton系统的分支结构
2010-05-28赵晓华
陈 强, 赵晓华
(浙江师范大学 数理与信息工程学院,浙江 金华 321004)
0 引 言
随着人类认识、改造和利用自然能力的不断提高以及实际应用的需要,经常需处理大量非线性问题.Hamilton系统是非线性科学研究中的一个重要领域,它的产生与发展具有深刻的实际背景[1].经典的Hamilton系统都是在偶数维相空间上定义的,这种结构虽然具有很好的性质,也有丰富的研究成果和实际应用[2],但也限制了其应用范围.为了使Hamilton系统的观点和方法能应用于实际研究中广泛存在的奇数维系统(一个最经典的例子是自由刚体定点转动的Euler方程,其相空间是3维的,由3个角动量轴构成),人们对经典的Hamilton系统进行了扩展,从而提出了广义Hamilton系统的概念[3].广义Hamilton系统是通过广义Poisson括号定义的,而广义Poisson括号是去掉非退化条件限制的Poisson括号.因此,用广义Hamilton系统可以研究奇数阶的非线性系统.广义Hamilton系统的Poisson流形(具有广义Poisson括号结构的流形)表示法是一种十分方便、有用的表示法.所以,Hamilton系统已由经典的(偶数维)形式推广为广义形式(任意维).
广义Hamilton系统作为经典Hamilton系统的推广,可以作为描述包括奇数维系统在内的更加广泛的非线性动力学问题的模型,在机械工程、光学、分子动力学等领域中都有很多的应用,其中很大的一类是具有球面叶层结构的广义Hamilton系统[2,4-5].在许多实际模型中,这种具有球面叶层结构的Hamilton系统模型,其Hamilton函数常以二次函数的形式居多.文献[6]已证明,对它的研究可以归结为对以下5类Hamilton函数所对应的广义Hamilton系统的研究:
1)H=w;
迄今为止,对前4种情况,相应的广义Hamilton系统在球面叶层上的平衡点分叉及其全局相图已被完全研究清楚[7-9].但对Hamilton函数中含4个参数的第5种情况,正如文献[10]指出的,其对应的广义Hamilton系统在球面叶层上的分叉及相图还未见相关报道.
基于此,笔者利用微分方程定性理论与动力系统分叉理论(特别是Hamilton系统相图分析技巧)研究了第5类Hamilton函数在λ=1时所对应的具有球面叶层的广义Hamilton系统,仔细分析了平衡点分叉及稳定性,获得了完整的全局相图分类.
1 平衡点分叉及稳定性分析

(1)
此时的Casimir函数为G(u,v,w)≜u2+v2+w2,其水平集是以(0,0,0)为中心的球面,记为ML={(u,v,w)|u2+v2+w2=L2}.由于C≠0,故可将式(1)改写为
(2)
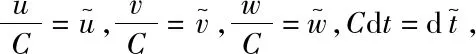
(3)

由上述讨论可知,只需对系统(1)在C=1时的参数进行讨论即可,即
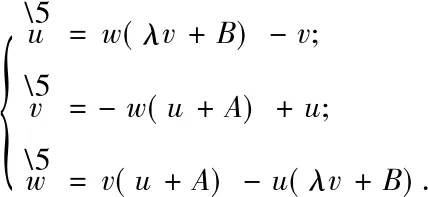
(4)
为了进一步简化研究其相图的性质,作如下对称变换:
(u,A)→(-u,-A);(v,B)→(-v,-B).
显然,系统(1)在此变换下保持H不变,说明只需要对参数A≥0且B≥0的情况进行讨论即可.
下面考虑系统(4)的平衡点个数及其稳定性随参数变化的分叉性质.由系统(4)的相空间具有叶层结构的性质以及Casimir函数可知,其平衡点由以下方程组确定:
(5)
经过化简可得平衡点(u,v,w)的分量v满足分叉方程
F(v)=A2v2(λv+B)2+v2[(λ-1)v+B]2+
(v2-L2)[(λ-1)v+B]2(λv+B)2.
(6)
与方程F(v)=0的根ve对应,可以得到系统(4)的平衡点q=(ue,ve,we),其中
(7)
为了弄清系统(4)平衡点q的稳定性,给出其Jacobi矩阵
其相应的特征方程为
|τI-Ja|=Bτ+τ3=0.
其中
B=ue(ve(λ-1)(-1-λ+2weλ)+
B(-we-λ+2weλ))+A(Bwe(λ-1)+
ve(1+we(λ-2)λ))+(-1-A2-
Bve(2λ-1)).
(8)
由此特征方程易知其3个根为:
根据微分定性理论[11]和广义Hamilton系统的性质可得命题1.
命题1平衡点类型与B的关系如下:
1)当B<0时,τ2,3为一对实数根,此时系统(4)的平衡点q=(ue,ve,we)为鞍点;
2)当B=0时,τ1,2,3为三重零根,此时系统(4)的平衡点q=(ue,ve,we)为尖点;
3)当B>0时,τ2,3为一对纯虚根,此时系统(4)的平衡点q=(ue,ve,we)为中心.
根据前面的讨论可知,系统(4)的平衡点q=(ue,ve,we)是由分叉方程(6)的解决定,而B的符号也是由分叉方程(6)的解决定.因此,接下来就讨论分叉方程的零根的个数随参数变化的分布情况.
考虑到分叉方程的复杂性, 笔者仅对λ=1的情形进行讨论.
当λ=1时,其特征方程为
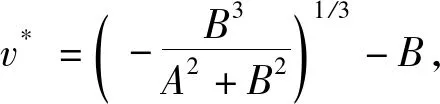
定理1
1)当ve>v*时,B1>0,此时系统(4)的平衡点q=(ue,ve,we)为稳定平衡点,并且是个中心;
2)当ve=v*时,B1=0,此时系统(4)的平衡点q=(ue,ve,we)为稳定平衡点,并且是个尖点;
3)当ve 接下来利用定理1判别在不同参数条件下系统(4)的平衡点个数和类型. 当λ=1时,此时关于v的多项式函数变为 F(v)=A2v2(v+B)2+v2B2+ (v2-L2)B2(v+B)2= (A+B)2v2(v+B)2+v2B2- L2B2(v+B)2. 则可分析得到: 1)当0 ①当0 ②当1≤L 2)当L=M时,由多项式根的分布可知f1(v)与f2(v)有1个切点和2个交点,多项式函数f1(v)与f2(v)的图像如图3所示.因为f1(v)=f2(v)有3个根v=v(1),v(2),v(3)(切点),v(1),v(2)>-B>v*,所以2个为稳定平衡点.当v=v(3)时,B1=0,所以也为稳定平衡点(尖点).即此时有3个平衡点e1,e2和e3,且都是稳定平衡点,并且是2个平衡点e1,e2为中心、1个平衡点e3为尖点. 图1 0 图3 L=M时f1(v)与f2(v)交点及根的分布图 图4 L>M时f1(v)与f2(v)交点及根的分布图 3)当L>M时,由多项式根的分布可知f1(v)与f2(v)有且仅有4个交点,即此时有4个平衡点,多项式函数f1(v)与f2(v)的图像如图4所示.设f1(v)=f2(v)的4个根为v(1),v(2),v(3),v(4).由函数f1(v)与f2(v)图像可知,v(4) 有了前面的平衡点分叉及稳定性分析,就可以研究系统(4)的球面叶层上的全局相图.由前面的参数分析可得: 1)当 0 如图5(a)所示,e1和e2为系统(4)的2个稳定平衡点,且都为中心. 2)当L=M时,系统(4)的相图为2个中心、1个尖点. 如图5(b)所示,e1,e2和e3为系统(4)的稳定平衡点,e1,e2为中心,e3为尖点. 3)当L>M时,系统(4)的相图为3个中心、1个鞍点. 如图5(c)所示,e1,e2和e3为系统(4)的稳定平衡点,e4为系统(4)的不稳定平衡点,e1,e2和e3为中心,e4为鞍点. (a)2个中心 (b)2个中心1个尖点 (c)3个中心1个鞍点 利用微分方程定性理论与动力系统分叉理论研究了二次Hamilton函数在λ=1时对应的具有球面叶层结构的广义Hamilton系统,仔细分析了平衡点分叉及稳定性性质,获得了对应的全局相图分类.但是,对此类二次广义Hamilton系统更一般的情况(λ≠1)还有待于进一步研究. 参考文献: [1]Arnold V I.Dynamical systems Ⅲ[M].Berlin:Springer-Verlag,1988. [2]Arnold V I.Mathematical methods of classical mechanics[M].2nd ed.New York:Springer-Verlag,1989. [3]李继彬,赵晓华,刘正荣.广义哈密顿系统理论及应用[M].北京:科学出版社,2007. [4]Pyshchev A P.Classical approach to effective rotational energy and bifurcation in rotational dynamics ofH2Xmolecules[J].Physical Review A,2003,68(4):1-10. [5]Zhilinski B I.Symmetry invariants and topology in molecular models[J].Physics Reports,2001,341(1/2/3/4/5/6):85-171. [6]Frauendiener J.Quadratic Hamiltonians on the unit sphere[J].Mech Res Commun,1995,22(4):313-317. [7]Lanchares V,Elipe A.Bifurcations in biparametric quadratic potentials[J].Chaos,1995,5(2):367-373. [8]Lanchares V,Elipe A.Bifurcations in biparametric quadratic potentials Ⅱ[J].Chaos,1995,5(3):531-535. [9]Lanchares V,Inarrea M,Salas J P,et al.Surfaces of bifurcation in a triparametric quadratic Hamiltonian[J].Physical Review E,1995,52(5):5540-5548. [10]Elipe A,Lanchares V.Exact solution of a triaxial gyrostat with one rotor[J].Celest Mech Dyn Astr,2008,101(1/2):49-68. [11]张芷芬,丁同仁,黄文灶,等.微分方程定性理论[M].北京:科学出版社,1985.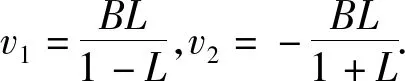

2 球面叶层上的全局相图

3 小 结
