教师如何引导学生动手操作

唐巍洋

认真审视现在课堂教学中学生的动手操作不难发现，相当多的操作活动只注重生动活泼的“形式”，追求课堂气氛的“热闹”，却缺少活动中数学思维的含量。在课堂教学中教师该如何引导学生进行操作呢?笔者以自己的教学经验与课堂所见，就本文作一些探讨。

一、有备而“动”——充分地导

操作活动应该以有充分的学具、教具准备为前提。教师在设计操作活动时，在认真钻研教材、掌握教学内容、确定目标的同时，要全面了解学生实际，做到教材、教况、学情了然于胸。然后确定教学中是否需要学生动手操作，用哪些学具进行操作，在什么地方设计操作。只有“万事俱备”，操作活动才能顺利开展，教师的引导才能有效、充分、到位，才能达到预期的效果。

二、明旨而“动”——有序地导

动手操作的过程是让学生感悟、理解和实现知识的“再创造”的过程，需要经历由易到难，由“扶”到“放”的过程。活动中如果一味地让学生自由操作、随心所欲，他们只能就事论事，为操作而操作，就不能从操作的过程中得到思维的提升。因此，教师在操作前应该向学生提出操作要求，让学生明确操作目的，知道通过操作要解决什么问题，克服操作的盲目性和随意性。

如，在教学《有余数的除法》时，课前每个学生准备15根小棒。

师：今天我们一起用小棒来学数学。用你们手中的小棒一份一份地摆，每份的根数要相同，每份可以摆几根?把你摆的結果记录在表格里。(学生根据教师的指导进行摆小棒，填表。)

师：观察表中的结果，你发现什么?可以分成哪几种情况?(生讨论回答，师根据摆的结果，列成除法算式。)

师：把多出来的小棒再分一份，行吗?为什么都不动手了?……

(师根据摆法列出除法算式。)

师：请大家仔细地观察，这些算式中的余数有什么特点?

教师有序引导，学生带着问题“一份一份地摆，每份的根数要相同，每份可以摆几根?”进行操作，明确了应该怎么操作，再根据教师出示的表格，更加清楚该在操作中找到什么知识。学生第一次摆，逐步理解了整除与有余数除法的区别，加深了对“平均分”的内化；第二次摆。“余下的数不能再摆一份了”，学生对有余数除法的特点——“余数比除数小”的理解，应比生搬硬套、死记硬背的记忆会印象深得多。

三、留时为“动”——有度地导

学生的操作活动既要有明确的要求，又要有一定的层次和开放性，为不同的学生的数学思考留有合理的时间与空间，才能确保操作的有效性，体现操作的价值。

如，某教师在教学《分数的初步认识》时，做了如下设计：

师：今天的学习任务就交给大家自己来完成。老师为大家提供了：一张圆形纸片、一块橡皮、一根一米长的绳子、一盒水彩笔、4个苹果图、一幅熊猫图。要求是：以1/2为例，运用这些材料，动手切一切、折一折、分一分。试一试能不能用不同的材料来说一说1/2的意义。(学生自由操作。)

师：谁愿意说一说，你是怎样表示1/2的?

生：把圆形纸片对折，其中的一份表示它的1/2。

师：还有其他表示方法吗?

学生纷纷举手展示自己的操作结果：把一块橡皮平均分成二份，每份是它的1/2；把一米长的绳子平均分成二份，每份是它的1/2；把一个苹果平均分成二份，每份是它的1/2……

师：请大家想一想，在表示1/2的过程中，有什么相同的地方?(它们都平均分成了二份。)

师：有什么不同的地方吗?(内容不同，有的是一个物体，有的是多个物体组成的。)引导学生归纳单位“1”。

师：刚才大家通过操作、讨论、分析、归纳得出：一个物体、一个计量单位、一个整体都可以看作单位“1”。把单位“1”平均分成二份，这样的一份都可以用1/2表示。

教师从学生已有的知识经验出发，灵活处理教材，把几个例题转化成了学生的操作材料——抓住1/2这一分数，给学生的操作留下了充分的探索空间与时间，学生通过充分地操作，相互交流，运用不同的材料说明了1/2的意义，突破了单位“1”这一难点，把分数意义上升为理性认识。

四、促思而“动”——有效地导

操作启动思维，思维服务于操作，在实践活动中学生动手、动脑、动口相互作用，使操作、思维、表达融为一体，有效地促进活动内化，从而达到智慧的生长和创造力的凸现。教师在指导学生操作时。必须把操作与思维活动有机结合起来，这样才能使学生由具体形象思维向抽象思维过渡。

1.在学生的认知生长点“动”。有效的学习不能单纯的依赖模仿与记忆。在学生认知生长处，教师应该让学生自己试一试，亲身体验知识的获得，而不是给他们“现成的”数学。如，在《直线、射线、角》的教学中，我是这样设计的：

师：通过学习，我们知道直线与射线都可以延伸，是画不完的。现在我们进行一个画线比赛。

师：(出示“·”)通过这个点画直线，猜一猜，可以画多少条?(生猜)

师：通过这个点，你在30秒的时间内可以画多少条直线。(计时，生画线。)

师：你画了多少条?(指名汇报)

师：看来在规定的时间内，大家画出的条数各不相同。如果时间无限多，你可以画多少条?说明了什么?(生充分发表自己的见解。)

师：(出示“··”)猜一猜，要同时经过两个点，可以画多少条直线?(生猜)

师：大家来试一试，答案就一目了然了。(生画线)

师：你想说什么?(生汇报)

让学生先猜猜，再试试，有效地“导”，引发学生有效地思维和有效地操作，思维“融”入“动”中，经历观察、猜测、操作、体验、思考的“动”，学生获得更为丰富、更为深刻的认知体验，他们的思维也将得以有效地发散，这样“做”出来的数学才让学生终生难忘。

2.在学生的认知冲突点“动”。教师在学生的认知冲突中创设情境，积极引导操作，“动”让思维经过碰撞进发火花。并把它引入一个更为广阔的空间。

如《认识圆的周长》一课，老师充分挖掘学生思维中的创新思维因素，创设多次认知冲突，让学生通过动手操作，亲历知识的形成过程。

师：龙潭湖公园有一个圆形花坛，为了保护花草，师傅们正准备沿着花坛围一圈篱笆，请你们帮忙计算一共需要多长的篱笆呢?请用手中的工具，小组合作探索周长的计算方法。(生操作)

生：把圆形纸片立起来放在刻度尺上滚动一圈，就测出了它的长度。

师：如果一个很大的圆形水池，要求它的周长，能用你们小组的方法把水池立起来在刻度尺上滚动一圈吗?(设置冲突，生再次进行操作。)

生：我们先用绳子在水池周围绕一圈，再量一量绳子的长度，就是水池的长度。

师：(拿出了一端系有小球的线绳，在空中旋转了一圈，又旋转了一圈。)小球走过的地方形成了一个圆，要想求这个圆的周长，还能用你们的方法吗?(再次设置冲突，生静默无语，再次进行操作。)

活动中的认知冲突让学生不断地操作，不断地把学生的思维推向一个个新的高潮，学生的思维从肤浅走向深刻，思维力度得到有力的提升。

3.在学生的知识拓展处“动”。创新源自良好的思维品质，而知识的拓展延伸处，是培养学生的发散思维，促进学生良好的思维品质形成的制高点。教师应抓住有利时机，在认知延伸处开展动手操作，让学生对所学知识进行巩固加深，并能创造性地进行运用。

如，在三年级《分数的初步认识》教学中，在学生明确了“平均分”的含义和初步认识几分之一后，在运用巩固知识的环节中，老师设计了操作练习，使“几分之一”的抽象概念得以“内化”“活化”。

师：拿出一张长方形纸，折出它的1/2。(生操作并展示：)

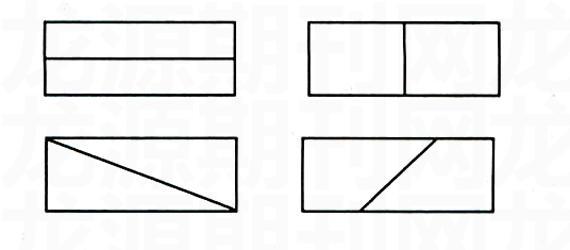
师：你是怎样折的?

师：这些表示1/2的纸片的形状相同、大小相等吗?为什么?(小组讨论)

……

师：请用另外两张长方形纸分别折出它的1/4、1/8，并涂上自己喜欢的颜色。折好后，同桌互相交流折的方法，说说每份表示它的几分之几?(生操作)

通过折、想、说、议等活动，进一步强化了对“平均分”的概念的理解，让学生的操作能力得到锻炼的同时，思维也得以发展。

五、“动”后反思——有味地导

心理学家认为，儿童思维发展的过程是内部的外部活动逐步内化的过程。操作固然重要，它能有效促进思维的发展。但只是一味地操作，而不注重操作后的展示、反思、交流、表述、概括，那操作只能是一场作秀，是为操作而操作的“空中楼阁”。因此，教学时，教师要鼓励学生用语言表述操作过程，对操作进行反思。这样，操作才能与思维有效、完美地结合，使思维更活跃，操作才更耐人寻味。

(责编林剑)