黄河非平衡输沙典型事例及其研究概述

2010-05-21江恩惠韩其为

中国水利水电科学研究院学报 2010年3期

江恩惠，韩其为

（1.中国水利水电科学研究院泥沙研究所，北京 100048；2.黄河水利科学研究院，河南郑州 450003）

长期以来，国内外的学术界和工程界都对冲积性河流的非平衡输沙问题投入了极大的关注。近年来特别是由于一些大的水利工程的修建引起的泥沙问题（如三峡工程）强有力的推动，使挟沙能力问题的研究从均匀沙向非均匀沙方面深化，并取得了一些重要成果［1-3］。以往对非平衡输沙的研究，主要有两类［4］。第一类［5-6］主要是从悬移质紊动扩散方程出发，求解出含沙量恢复饱和过程的解析解或者数值解。第二类［2］是以韩其为为代表的引入含沙量恢复饱和系数直接推求平均含沙量沿程变化的研究。这类预报十分简便，在我国得到了广泛应用。但对于恢复饱和系数的取值目前仍停留在经验阶段。

众所周知，水库或河道的冲淤变形多集中在每年汛期，特别是汛期的头一场或几场较大洪水过程。如黄河干支流多年平均汛期来水来沙分别占全年总量的80%和90%，冲淤量也在70%以上。天然河流中（如黄河、长江）汛期的水流泥沙相互作用表现为强烈的非恒定、非均匀泥沙输移现象。尤其黄河泥沙含量比较大，非平衡输沙问题更加突出，也产生了“洪峰增值”、“驼峰河段”等一些典型现象，并引起了广泛的关注，不少专家学者也对这些问题做了大量的研究，作者在此通过近几年的研究对黄河非平衡输沙产生的典型事例相关研究成果，做以简单总结，有些观点带有探索性质，供同行专家批评指正。

1 黄河下游调水调沙期间的“洪峰增值”现象及其研究成果综述

1.1 洪峰增值现象小浪底水库自1999年汛后运用以来，为黄河下游河道防洪、减淤、引水灌溉及防凌等发挥了重要作用。但在水库蓄水拦沙与异重流排沙运用时，下游河道水沙演进出现了一些新的异常现象，主要表现为水库异重流排出高含沙洪水后，下游洪峰出现增值，且增幅很大。2004年8月22日14时至30日12时，小浪底水库实施异重流排沙运用，出库最大洪峰流量为2680m3/s，实测最大含沙量352kg/m3，平均含沙量112 kg/m3，泥沙颗粒级配较细，中值粒径平均约0.008mm。期间沁河、伊洛河流量之和不足200 m3/s，水流几乎为清水，而演进到下游128km的花园口站，实测最大洪峰流量却高达3990 m3/s，洪峰增值达38.9%，孙口两站最大洪峰实测值与夹河滩站接近，从而出现了小浪底到花园口河段洪峰流量急剧增大、夹河滩至孙口河段几乎不削峰的异常现象［7］。

洪峰增值现象也是黄河非平衡输沙的一个典型现象。这一现象在20世纪70年代就发现了，但一直未得到圆满解释，而“04.8”洪水洪峰异常增值现象出现后，受到了很多治黄科技工作者的高度重视，并相继提出了很多关于洪峰异常增值成因的观点，如“局部沙坝”、“浆河阵流”、“挤压或聚集”、“孤立波”、“水跃”等［8］。但这些观点均无法成功解释“04.8”和“05.7”洪水洪峰增值的原因。在“04.8”洪水期间，并无资料反映黄河下游出现“局部沙坝”，即使出现少量的“局部沙坝”，也不能保证洪峰流量一直到孙口也不削峰；此外，“04.8”水沙过程与河道边界特性不具备出现“浆河阵流”、“孤立波”及“水跃”的条件；对于“挤压或聚集“，在任何一场洪水涨峰过程中，均存在这一问题，因此这与洪峰异常“增值”表现无关。

李国英［9］、江恩惠［10］等通过对“洪峰增值”现象的系统研究，认为糙率的减小是洪峰增值的主要原因。

1.2 洪峰增值理论研究

1.2.1 基于力学分析的洪峰增值机理研究江恩惠等通过选取单位河宽的河流微段（见图1），对运动水流中一微小流段进行受力分析，推导出［10］。

式中：u为水流瞬时流速；t为时间；g为重力加速度；Jf为附加比降； β0为河床底坡角度；h为平均水深；n河道综合糙率。

认为对于某一特定的河流、特定的涨峰过程而言，式（1）中第一项的两个因素，河流底坡在一场洪水期间不会出现较大的调整；同时，附加比降的变化也不会太大。然而，受河道边壁及挟沙水流内部结构调整变化的影响，式（1）中第二项对水流加速度的影响有时可能表现的较为突出。分析第二项的因素组成可以看出，水流的平衡比降与糙率有直接关系，说明糙率的变化将直接影响洪水演进加速度的变化。糙率增大，水流减速，槽蓄增加，洪峰坦化；糙率减小，水流加速，洪峰增值。

1.2.2 基于水动力学的洪峰增值机理研究天然河道中的洪峰演进过程，主要受上游来流条件、河道前期水流条件、河道形态及水流与河道之间的相互作用关系等方面的影响。李国英［7］基于一维水流运动方程整理简化，得方程（2）：

式中：Q0为t0时刻、x0位置的断面平均流量Q0(t0,x0)；Qi为水流从x0位置历时(ti-t0)后在xi位置的断面平均流量Qi( )ti,xi，ti＞t0，xi＞x0，if为河道水力坡度（包括床面阻力、自由表面风应力等；通常由曼宁公式确定，即为水面坡度，其他符号意义详见文献［7］。

由式（2）可知，洪水是否出现流量增值，取决于iw是否大于if。文献［7］对此进行了深入分析，认为洪水能否发生洪峰增值，主要取决于河床阻力减小的幅度大小，即取决于河道糙率减小的幅度大小。

综合以上两种分析表明，对于不漫滩洪水而言，洪水在河槽中演进，前期的清水过程，对河床冲刷，河床发生粗化，随着高含沙水流的到来，特别是含有极细沙的水库异重流在河槽中的演进，前期被粗化的河槽会附着泥浆，以至减小壁面及河床底部的糙度，使阻力系数明显减小。因此，后续水流流速加大，并逐渐赶上前方水流，发生洪峰叠加。

1.3 减阻水槽试验江恩惠［11-13］等开展了相关减阻水槽试验，试验在长22m、宽0.3m、高0.5m的玻璃水槽中进行，试验主要在3种床面条件下开展，底部分别为光滑水泥面、加糙床面及粗糙水泥面。水流循环时，搅拌池中的浑水经过电磁流量计以及输水管道流向水槽，再经过回水池返回搅拌池，以此保持长时间水的循环以及含沙量的稳定。试验中所采用的3种原型沙，其中值粒径d50分别为0.0077m、0.011mm和0.019mm。

水槽试验表明：含有极细沙的水流对河道有一定的减阻作用，这再次说明了小浪底异重流排沙期间河道糙率有减小的可能性；在光滑水泥面以及在光滑水泥面上加糙的床面形态，有减阻现象但不很明显；在粗糙床面上，糙率系数随着含沙量的增大而减小，但当含沙量为60～100kg/m3时，糙率变化比较平缓，超过100kg/m3时，糙率又随含沙量的增加而减小；对于不同级配的悬沙，当含沙量超过某一临界含沙量以后，糙率随含沙量的增大而减小，且细颗粒含量越大，减阻现象越明显。

1.4 数学模型在实时预测的应用江恩惠、赵连军［7，10］通过对黄河下游高含沙洪水期河道糙率变化规律研究，建立了黄河下游糙率公式，完善了黄河下游准二维非恒定流水沙数学模型，并模拟了2004、2005年黄河调水调沙期间异重流高含沙洪水在下游河道演进过程中发生洪峰增值的变异现象，模型计算成功复演了这两年的洪峰增值情况。在2008年调水调沙期，当小浪底水库异重流排沙实施之后，利用该模型进行了跟踪预报计算，模型计算的花园口量大洪峰流量为4620m3/s，与实测资料非常接近，增值过程与实测资料也基本一致。

2 “驼峰”河段的形成原因

2.1 “驼峰”现象 “驼峰”河段现象是对近期黄河下游各河段排洪能力不一致，表现为“上下大、中间小”，类似骆驼峰的形象称呼，来源于反映排洪能力的指标——平滩流量在下游河道的沿程变化过程（图2）。随着2002年以来调水调沙试验和生产实践的进行，下游全程发生了明显冲刷，河槽面积有效扩大，过洪能力显著增加。但是相对于上下游河段，高村—艾山河段过洪能力增大幅度仍较小，到2008年汛前高村以上平滩流量超过5000m3/s、泺口以下平滩流量超过4000m3/s，但高村—艾山仍未达到4000m3/s，排洪能力“上下大、中间小”的“驼峰”现象仍然存在，成为调水调沙的瓶颈河段，限制了大流量的泄放，影响到调水调沙冲刷河道的效果。

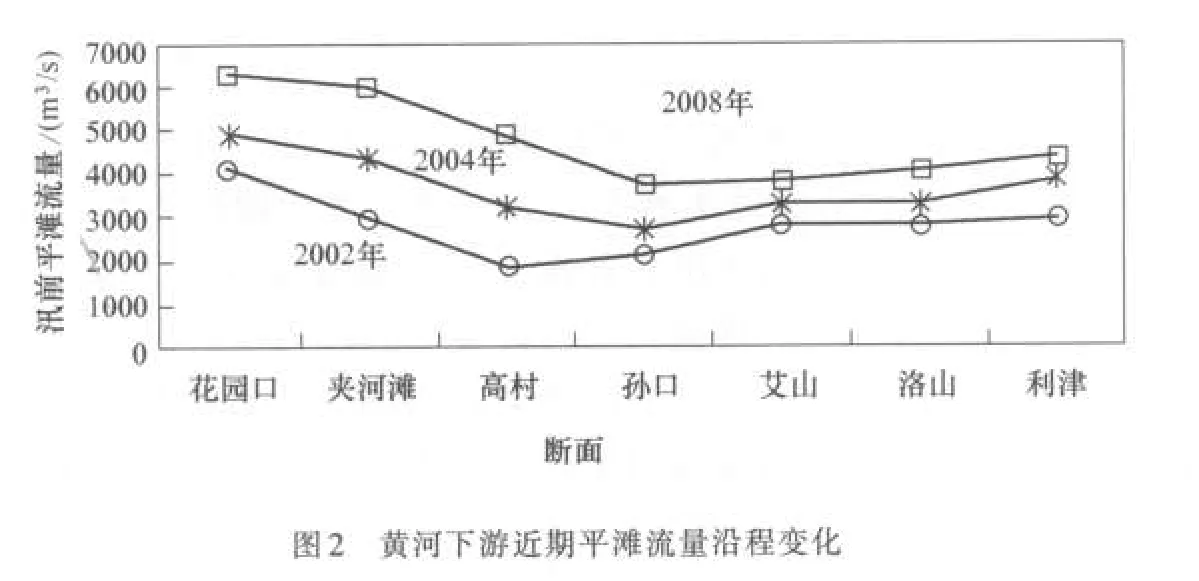
“驼峰”河段的存在是河流在自我塑造过程中的一个自然现象，也是黄河下游非平衡输沙的一个典型现象。实际上，“驼峰”河段在过去一直有，但是由于社会因素和经济条件决定了在不同时期人们关注问题的不同，另外不同时期治河的聚焦点也是不同的，在以前“驼峰”河段的概念提得相对较少。但是20世纪90年代以来，随着河槽快速、急剧的萎缩，特别是随着科学治河理念的进步，目标要求的进一步提高，技术手段完善，调度要求的精细等，“驼峰”河段的问题也就日益突出［14］。

2.2 “驼峰”河段形成原因研究

2.2.1 资料分析张晓华［15］、夏军强［16］等对“驼峰”河段的形成原因做了初步的分析，结合其相关成果及相关试验研究成果，认为“驼峰”河段的形成原因主要有以下因素组成。

（1）水沙关系不协调是“驼峰”河段形成的前提条件。“驼峰”河段的形成与不协调的水沙关系有着紧密的联系。资料分析表明，1950年代黄河下游基本上是槽淤积20%左右，滩淤积80%左右。但是，1986年以后，主槽淤积70%，滩地淤积30%。据统计，1986—1999年黄河下游主槽淤积量占全断面淤积量的比例达到72%，是各时期中比例最高的。高村—艾山河段的滩地淤积比也接近70%。

河道萎缩、洪水明显减少，导致在非漫滩洪水的淤积比重占到全淤积量的比重明显增加，为“驼峰”河段的形成奠定了基础。

（2）河床纵剖面的影响。高村至艾山河段，位于黄河桃花峪冲积扇与东坝头冲积扇两个的叠加区，该河段的地形条件也决定了该河段一直处于淤积抬升之中。一般河流纵剖面的形态和河床比降的变化，与地形的初始条件相适应。也就是说，纵剖面的形态和比降大小受地形轮廓所制约。从黄河下游河道的形成来看，苏泗庄—孙口河段的地形条件决定其比降较缓，影响到高村—艾山河段的河道冲淤，更易于淤积。

（3）其它因素对“驼峰”河段的影响。高村—艾山为黄河下游过渡型河段，艾山以下为弯曲型河段，河道逐渐变窄，形成的卡口对“驼峰”河段有一定的影响。该河段的浮桥建设密度较高以及引水等，对“驼峰”河段的形成也有一定的影响。

2.2.2 数学模型模拟研究赵连军［17］等在开展黄河下游河道不同治理模式未来冲淤预测研究中，利用准二维非恒定流水沙数学模型对165年水沙系列进行了计算。计算结果表明，165年内在黄河现状方案下小浪底—利津河段河道平均抬升了4.84m，平均淤积速率为0.029m/年。其中，抬升最高的是孙口—艾山河段，共抬升了8.73m；抬升最低的是小浪底—花园口河段，共抬升了3.49m，见表1所示。在4000m3/s的流量下，计算的165年初始与最终的水位抬升值，如表2所示。也表明在孙口—艾山段抬升的最高。说明该河段从输沙上来讲，是易形成“驼峰”河段的。

表1 165年后黄河下游各河段累计淤积厚度计算值（单位：m）

表2 流量为4000m3/s时各站165年后水位抬升值（单位：m）

2.2.3 治理措施水沙关系不协调是“驼峰”河段形成的主要原因，对于“驼峰”河段的治理首先就是要改善这种不协调的水沙关系，目前黄河水利委员会开展的水沙调控体系的建设以及调水调沙的运行，对“驼峰”河段的改善起到了积极的作用；其次，可以通过改变河道不利的边界条件来改善“驼峰”河段的不利态势，如通过挖河疏浚等措施；通过改变“驼峰”河段下游东平湖水库的运用方式，适机选择洪水冲刷艾山以下河道，不但艾山以下河道的过洪能力会得到恢复，而且还能起到降低“驼峰”河段侵蚀基准面的作用，对“驼峰”河段的治理有一定作用；同样，黄河河口的综合治理，也会有利于“驼峰”河段不利形态的改善。

3 结语

通过对黄河非平衡输沙几个典型事例分析，认为挟带极细沙的水流会引起河道糙率的减小，在一定的条件，调水调沙期间就会出现“洪峰增值”现象，对黄河防洪极为不利，因此通过数学模型开展洪峰值的预报十分必要；“驼峰”河段主要是由于不协调的水沙关系及地质条件影响逐步形成的，可以通过构建水沙调控体系，开展调水调沙结合挖河疏浚，改善“驼峰”河段不利形态。

本文列举的黄河中的一些特殊现象都属于非平衡输沙的范畴，这些特殊现象也为黄河治理开发带来许多问题，也是黄河研究中最复杂、最困难的问题。受制于人们对河流泥沙动力学的认识、实测资料的匮乏以及测量仪器的限制，对上述问题的研究有待于开展更深入的研究，为黄河的长治久安提供科学的理论支撑。

［1］韩其为，何明民.论非均匀悬移质二维不平衡输沙方程及其边界条件［J］.水利学报，1997（1）：1-10.

［2］韩其为.非均匀沙不平衡输沙的理论研究［J］.水利水电技术，2007，38（11）：14-23.

［3］乐培九.关于非均匀沙悬移质不平衡输沙问题［J］.水道港口，1996（4）：1-7.

［4］刘金梅.沙质河道冲刷不平衡输沙机理及规律研究［J］.水科学进展，2003，14（5）：563-568.

［5］侯晖昌.河流动力学基本问题［M］.北京：水利出版社，1982.

［6］张启舜.明渠水流泥沙扩散过程的研究及应用［J］.泥沙研究，1980（1）：37-52.

［7］江恩惠，赵连军，张红武.多沙河流洪水演进与冲淤演变数学模型研究及应用［M］.郑州：黄河水利出版社，2008.

［8］李勇，周家胜，孙赞盈，等.有关黄河下游流量沿程增大的各种观点评述［J］.泥沙研究，2006（4）：78-81.

［9］李国英.黄河洪水演进洪峰增值现象及其机理［J］.水利学报，2008，39（5）：511-527.

［10］江恩惠，赵连军，韦直林.黄河下游洪峰增值机理与验证［J］.水利学报，2006，37（12）：1454-1459.

［11］朱长军，郝振纯，江恩惠，等.挟极细沙水流的明渠综合糙率系数变化规律研究［J］.三峡大学学报(自然科学版），2008，30（5）：1-3.